C.3 EF et maillage

C.3 EF et maillage

C.3.1 Types d’éléments finis

Avant toute chose, l'utilisateur d'un programme EF doit veiller à la bonne compréhension du vocabulaire utilisé par le logiciel : barre/poutre, plaque/coque, surface/panneau, etc…

Une partie théorique est consacrée aux éléments finis en Partie 1 § A.3. En particulier, les différents types d’éléments y sont décrits.

L’utilisateur est invité à consulter la notice de son logiciel concernant chacun des éléments finis pour vérifier ses degrés de liberté, et les efforts et déformations qu’il prend en compte, éventuellement avec des options à activer ou désactiver.

Les questions à se poser sont les suivantes. En fonction du problème à résoudre, veut-on :

C.3.2 Forme du maillage

La première partie du présent guide (Partie 1 § A.3) a détaillé les différentes formes possibles de maillage pour les éléments surfaciques (triangles, quadrilatères) et pour les éléments volumiques, ainsi que les conditions d’utilisation de ces différentes formes.

On ne décrit ici que les règles à suivre, une fois que le type de maillage a été choisi.

La plupart des logiciels ont des mailleurs automatiques, avec parfois de nombreuses options pour améliorer et personnaliser le maillage.

Le conseil principal est de rechercher le maillage le plus régulier possible, mais de raffiner néanmoins là où cela est nécessaire.

Dans certains cas et en fonction du logiciel utilisé, il est plus intéressant de mailler manuellement. On obtient ainsi des mailles régulières, dont on peut maîtriser la numérotation, ce qui facilite l’application des charges et l’exploitation des résultats.

Il y a des règles sur l’élancement des éléments (le rapport entre la plus petite et la plus grande dimension doit être supérieur à 1/3) et sur la distorsion (respect de la planéité des éléments). Les éléments distordus peuvent nuire à la pertinence des résultats. Pour un calcul non linéaire, par exemple, si un élément très distordu au départ se trouve dans une zone à forte déformation, la distorsion de cet élément peut s’accentuer entraînant une interruption du calcul, du fait d’un dépassement des critères limites. Certains logiciels le signalent. Il y a également des règles à respecter sur les angles ou ratio d'aspect des éléments. Certains logiciels peuvent tester l'ensemble des mailles vis à vis de ce critère, le cas échéant, en le pondérant par la surface relative de l'élément fini.

Exemple de détection d'EF ne répondant pas à un critère de ratio donné

Le ratio d'aspect d'un triangle est la valeur 2Ri/Ro, où Ri est le rayon du cercle inscrit au triangle et Ro le rayon du cercle circonscrit. Cette valeur est comprise entre 0 et 1. Plus la valeur est proche de 1, meilleure est la qualité du triangle ; c'est le cas pour les triangles équilatéraux. A contrario, lorsque l'aire du triangle est nulle, le ratio d'aspect vaut 0.

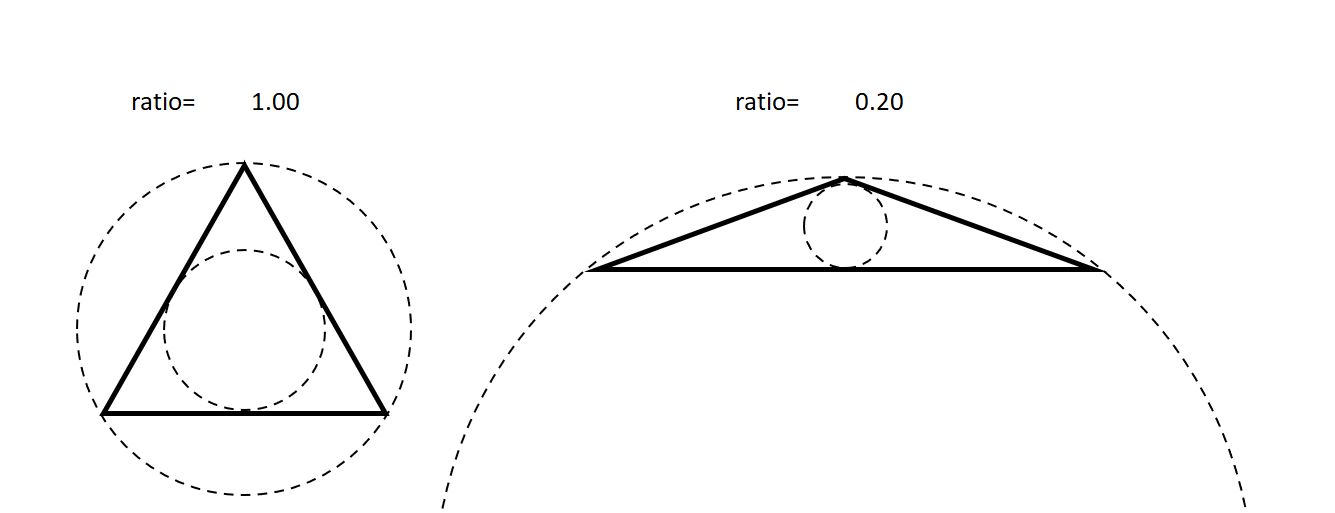
Illustration de la définition du ratio d'aspect

On peut retenir qu'un triangle est dégénéré quand son aire tend vers 0.

Dans tous les cas, il faut regarder la forme et l’allure du maillage.

Si l’allure n’est pas bonne, il est toujours possible de tester une autre option de maillage, de créer des nœuds ou de redécouper les plaques pour que le maillage s’améliore.

Le rapport entre la plus petite et la plus grande dimension d'un élément doit être supérieur à 1/3 et le ratio d'aspect doit tendre vers 1.

Exemple: soit un parallélépipède de 160x160x160 mm³ avec une face présentant un cercle. On souhaite avoir une taille moyenne de maille d’environ 40 mm sauf au centre du cercle où on désire avoir une taille moyenne de 2 mm. 1er maillage : la modélisation des surfaces est réalisée de manière élémentaire. Dans un premier, le maillage de la surface circulaire est effectué avec une taille de maillage de 2 mm. On procède ensuite au maillage des surfaces restantes avec une taille moyenne de maille de 40 mm (en général, le maillage des surfaces va s’effectuer en suivant l’ordre de création des surfaces). 2ème maillage : la modélisation des surfaces est améliorée. Le maillage est piloté en partant de la surface centrale.

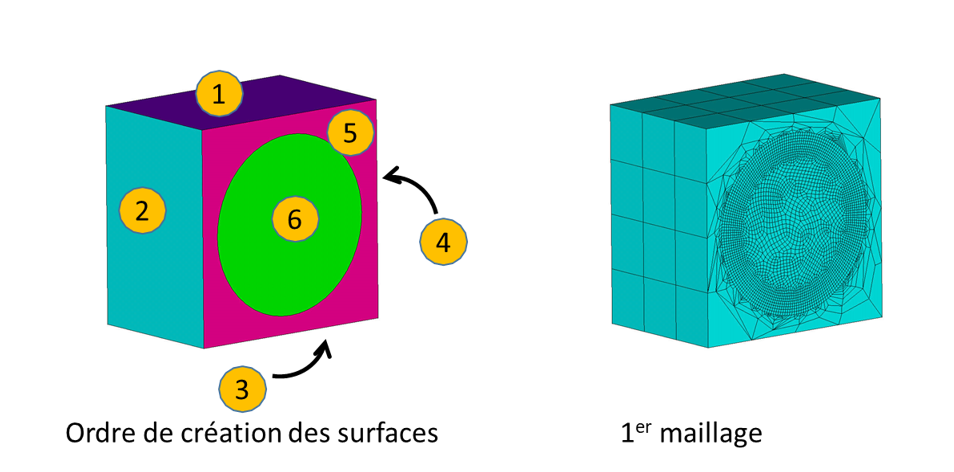
Modélisation surfacique élémentaire = Maillage non régulier + éléments dégénérés

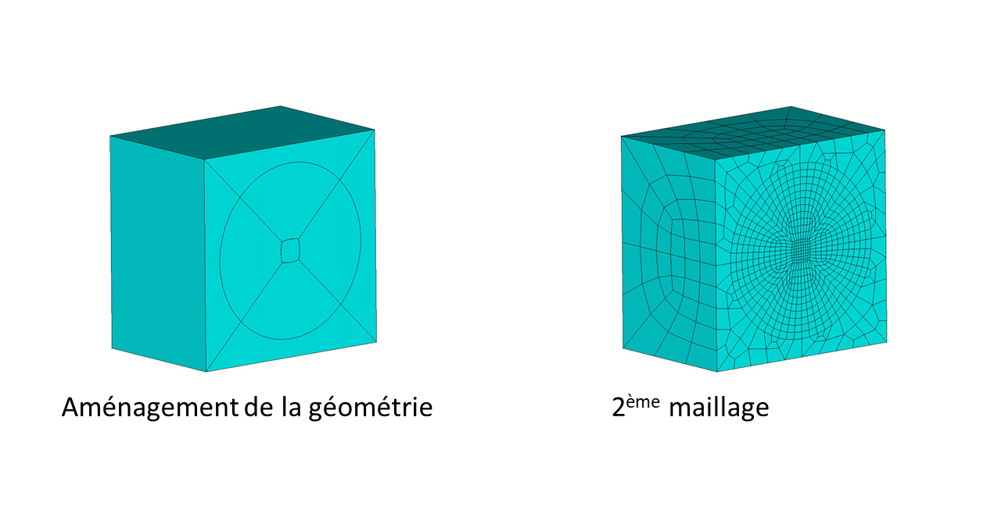
Modélisation surfacique améliorée + Maillage piloté = Maillage et éléments satisfaisants

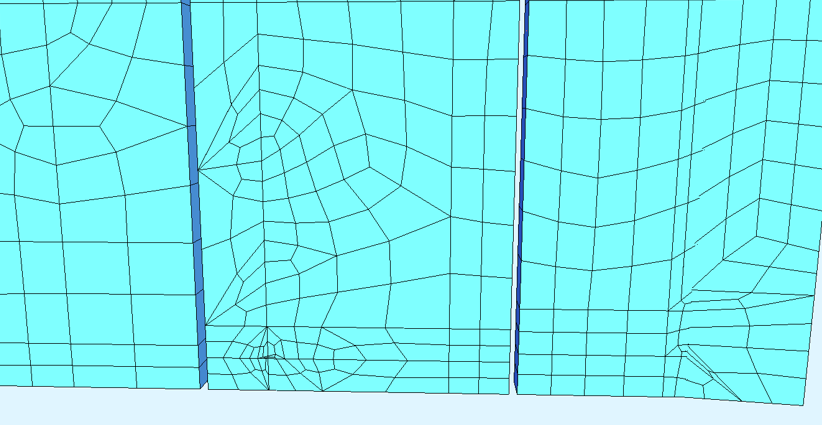
Exemple de maillage dégénéré

Un bon maillage est toujours « esthétique », il ne doit pas choquer visuellement.

C.3.3 Taille du maillage

Les objectifs des calculs doivent rester présents à l’esprit pour fixer la taille du maillage.

Tout d’abord, dans un modèle, il faut distinguer les éléments pour lesquels on veut des résultats des éléments qui sont là pour reproduire la rigidité et la masse de la structure.

Pour des éléments surfaciques et pour les éléments où l’on veut des résultats, il est d’usage de respecter une taille de maillage comprise entre 1 fois et 2,5 fois l’épaisseur de l’élément.

Pour les éléments pour lesquels on n’attend pas de résultats, on peut adopter des tailles plus grandes.

Les zones présentant un intérêt particulier dans l’analyse des résultats et susceptibles de présenter un fort gradient de contraintes et de déformations doivent donc présenter un raffinement de maillage suffisant et le moins possible d’éléments dégénérés.

Exemple d’un maillage raffiné dans les coins du bâtiment via un raffinage à partir d’un point émetteur (raffinage du maillage sur une approche concentrique) afin d’appréhender les problèmes de gradient thermique dans les planchers:

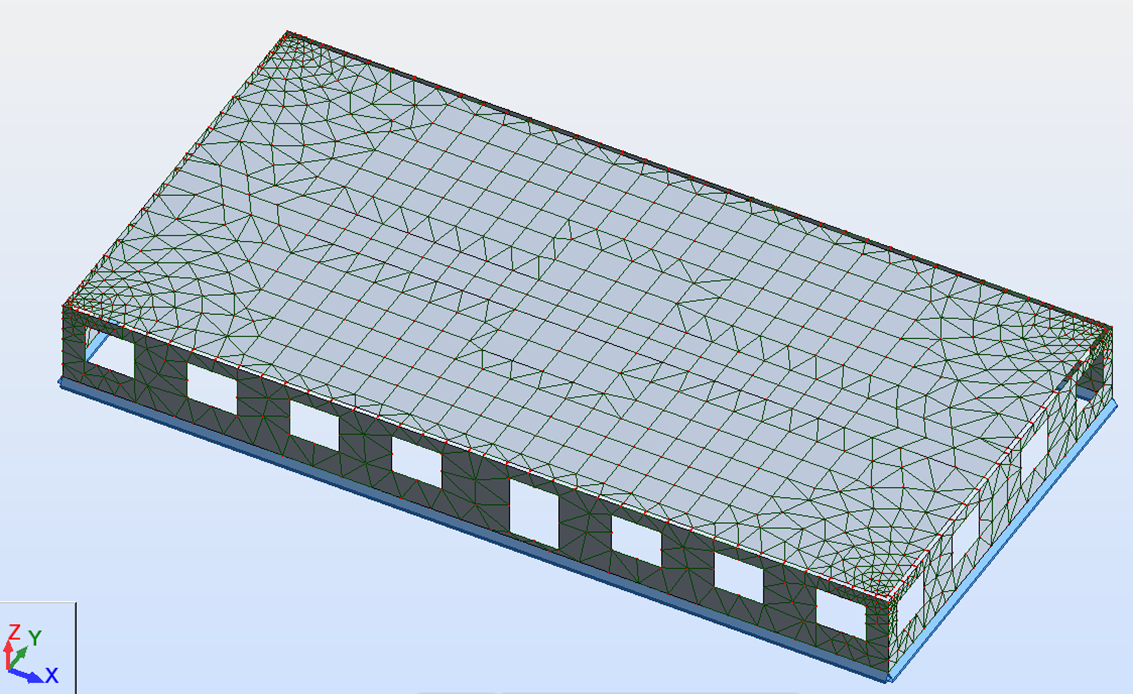
Il convient de veiller à ce que l’évolution du maillage d’un point à l’autre du modèle soit progressive. Lors du passage d’une zone à l’autre, le maillage ne doit pas présenter de variation trop brutale.

La taille du maillage doit aussi être adaptée aux capacités du logiciel et au temps de calcul disponible. Il peut s'avérer utile, avant de se lancer dans le modèle réel, de produire un modèle à la géométrie très simplifiée (voiles parallèles ou orthogonaux, absence des poutres et trémies…) et de lancer les calculs, pour vérifier que le logiciel arrive au bout - et si c'est le cas, dans un délai raisonnable - puis qu'il est capable de traiter les résultats de manière fluide, en particulier si l'on a des calculs multimodaux à produire.

Une analyse de sensibilité (en divisant ou multipliant par deux la taille de la maille et en comparant les résultats - voir paragraphe suivant sur les tests de finesse) permet de caler la taille optimale sans mobiliser des ressources superflues.

Pour les éléments filaires en calcul linéaire, le problème est moindre, car les résultats des éléments finis découlent de la théorie des poutres et ne dépendent pas du maillage. En revanche, l’affichage des résultats peut être trompeur et une règle classique est d’avoir une discrétisation de l'ordre du 1/10ème de la portée.

Pour les calculs non-linéaires, il est d’usage de raffiner le maillage à proximité des zones de plastification.

Pour la modélisation du sol, en calcul sismique, on respectera une taille de maille inférieure ou égale au 1/10ème de la longueur d’onde excitatrice (voir Partie 1 § F.8).

C.3.4 Test de finesse du maillage

Un test souvent réalisé consiste à procéder à deux calculs identiques sur le même modèle, à la différence près que pour l’un d’entre eux, la finesse du maillage est améliorée dans un rapport d'un à deux. Les résultats principaux donnés par ces deux calculs sont comparés sur les zones d’intérêts.

Cet exercice permet d’ajuster la finesse du maillage aux objectifs de l’analyse. Le temps de calcul variant exponentiellement avec le nombre de degrés de liberté du modèle, la réduction du nombre d’éléments, si elle n’induit pas de perte sur la qualité des résultats, peut être appréciable en termes de temps d’immobilisation de l’ordinateur et en termes d’espace disque nécessaire au stockage des résultats.

Inversement, il peut s’avérer nécessaire d’affiner le maillage afin que les résultats soient valides mais généralement ce raffinement ne sera réalisé que sur les zones d’intérêts.

Les indicateurs de qualité de maillage fournis par les logiciels portent sur la forme et la distorsion des éléments, et non pas sur la pertinence de la taille du maillage. Le test de finesse est donc toujours utile, notamment pour les gros modèles.

A noter l’existence de quelques rares logiciels qui disposent d’une capacité de maillage adaptatifs en fonction des chargements et des déformations (cette option est plutôt utilisée pour des calculs non-linéaires).

Illustration

Exemple de l’impact de la taille du maillage sur les résultats dans un plancher - de haut en bas, maillage de 20, 40 et 80 cm, respectivement. Le cisaillement maximal qui est égal à 0.92 MPa avec un maillage de 20 cm passe à 1.49 MPa avec un maillage de 40 cm et à 1.22 MPa pour un maillage de 80 cm.

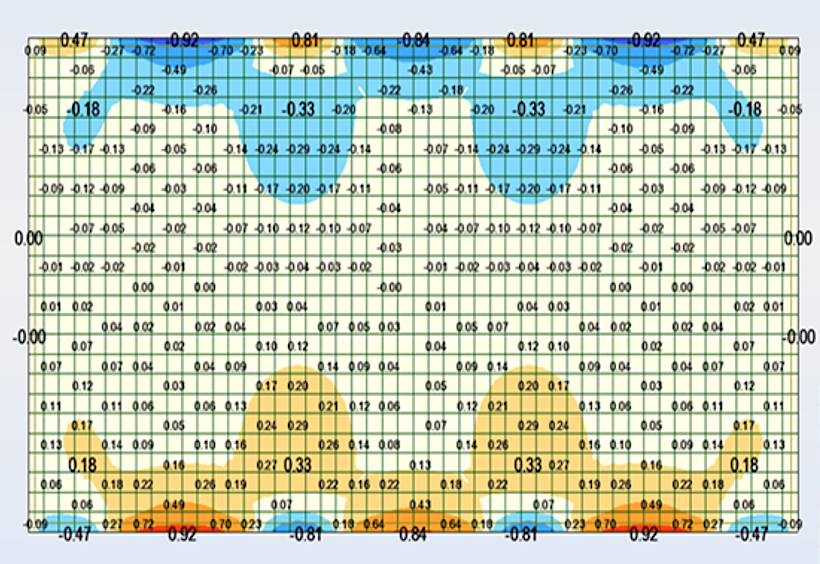
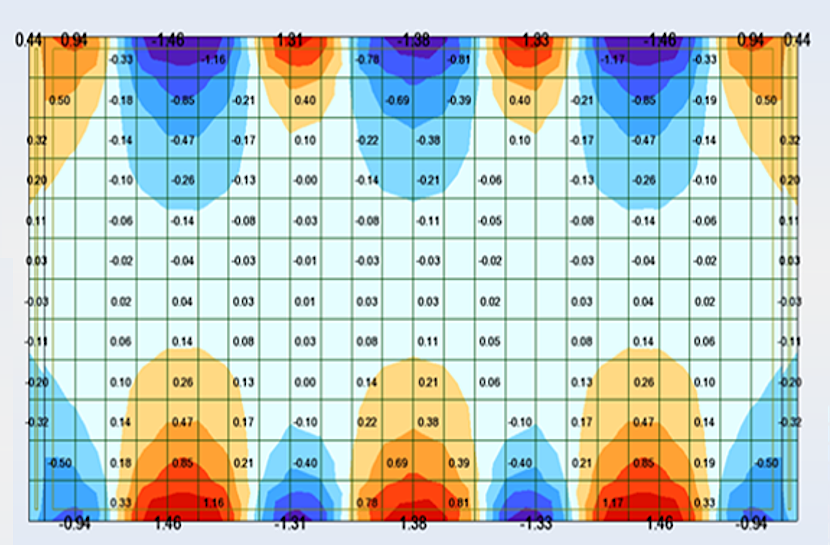
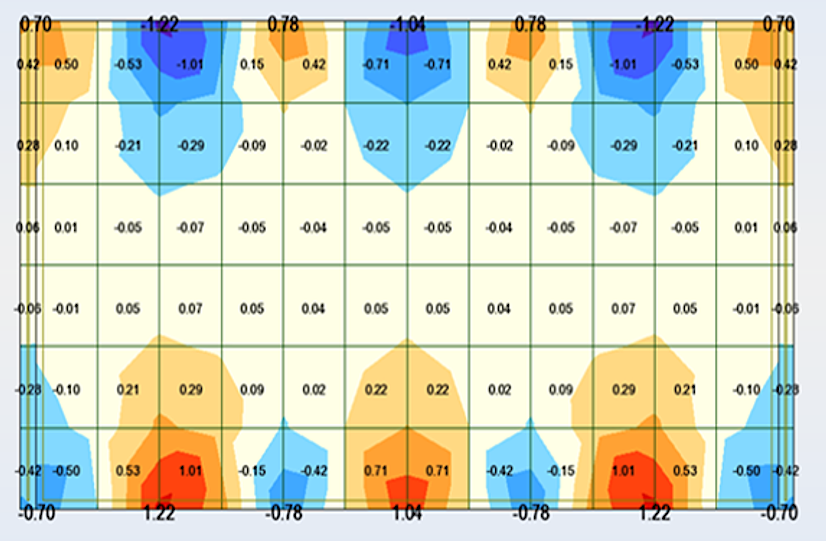
C.3.5 Orientation des repères locaux

L’orientation des éléments a une répercussion importante lors du post-traitement des résultats.

La vérification des repères locaux doit se faire de préférence avant l'introduction des chargements du modèle, ces derniers pouvant être subordonnés aux axes locaux des plaques.

Pour les éléments filaires, l’axe X des éléments de poutres est usuellement dirigé du point « origine » au point « extrémité », les axes Y et Z étant en théorie positionnés de manière quelconque par rapport à cet axe X. Or la position de ces axes Y et Z doit être homogène pour les éléments d’une même famille, d’une part pour faciliter l’application des charges transversales (par exemple une charge de vent) et d’autre part pour la lecture des contraintes en fibres extrêmes qui sont définies par translation selon Y et Z de la fibre neutre.

Dans la plupart des logiciels, les axes locaux des éléments sont orientés par défaut soit par rapport au repère global du modèle (alignement du Z local avec le Z global), soit par rapport à l’ordre de création des entités. On peut toujours forcer une orientation homogène sur un ensemble d'éléments.

Pour les éléments 2D, de la même manière :

Exemple: Plaque et repères locaux des éléments

Sujet : le sens de définition des plaques peut, pour certains logiciels, générer l’orientation des repères locaux des éléments.

Exemple : Plaque 6×6 m² (modélisée avec 2 plaques de 3×6 m²), appuyée sur 4 côtés, charge de 3 T/m²

Vue des repères locaux des éléments

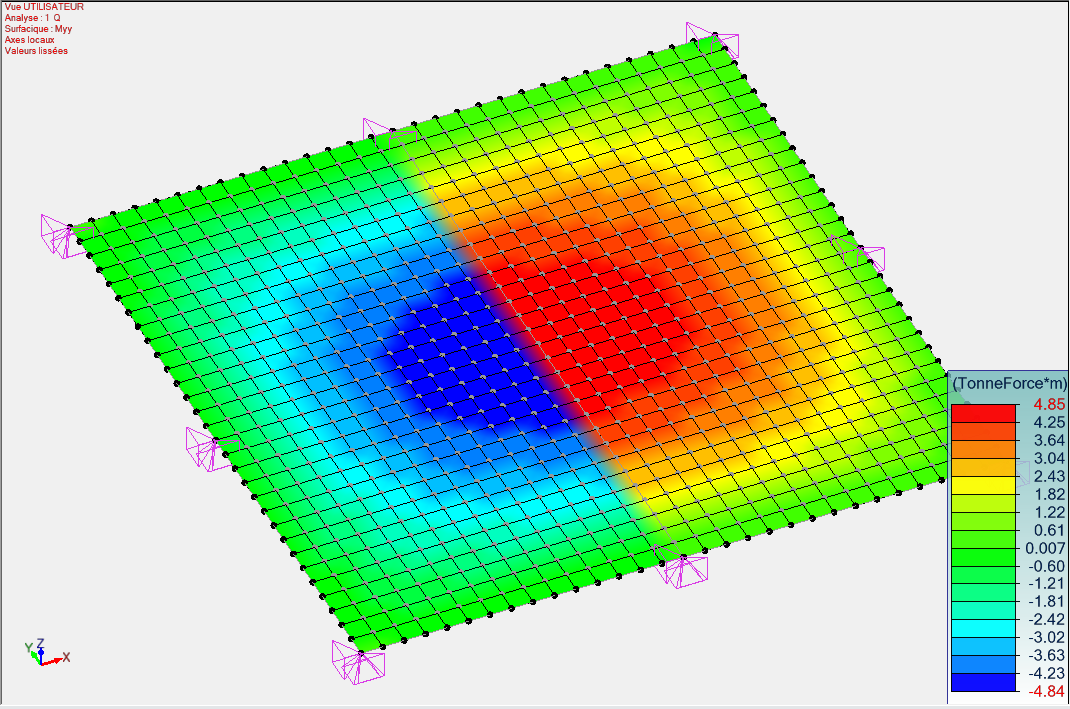
Vue des moments de flexion

On note alors une brusque discontinuité des moments sur la ligne de liaison entre les deux plaques. Cette discontinuité, qui n’a aucune origine réelle, est uniquement due à la modification d’orientation des repères locaux.

En particulier, le changement d'orientation de repères comme ci-dessus, posera problème si l'on demande au logiciel de calculer des efforts moyens dans une coupure donnée…

Vérifier que tous les repères locaux ont la même orientation.

C.3.6 Taille de modèle

Le temps de calcul est souvent déterminant dans l’économie du projet. Il est donc toujours intéressant de chercher à optimiser ce temps de calcul.

Le temps de calcul d’un modèle dépend de nombreux paramètres :

En fonction du logiciel, on peut souvent optimiser la quantité de données à sauvegarder et le nombre de degrés de liberté.

Sur un projet courant, un modèle va tourner au moins une vingtaine de fois. Tout gain sur le temps de calcul est très vite appréciable.

Il est inutile de sauvegarder systématiquement les fichiers de résultats, en particulier si le modèle tourne en moins de deux à trois minutes. Ces fichiers ne font qu'encombrer des clouds gros générateurs de CO2.

C.3.7 Option « Merge » ou « Fusionner »

La plupart des logiciels ont des fonctions permettant de fusionner les nœuds ou les points de construction géométriques qui sont très proches en fonction d’une tolérance définie par défaut ou par l’utilisateur. Cela permet d’éviter les discontinuités de maillage.

Cette opération présente certains risques, notamment en présence de joints de dilatation ou d’absence de soudure que le modèle pourrait ignorer.

En cas de présence de joints, l’utilisateur a le choix entre :

L’opération de fusion peut aussi impacter les asservissements entre les nœuds. C’est pourquoi les asservissements et les liens mécaniques entre nœuds doivent être définis après le « merging ».

C.3.8 Groupe d’éléments (pour la visualisation et l'exploitation ultérieure)

La plupart des logiciels offrent la possibilité de définir des groupes des nœuds ou des groupes d’éléments.

Cette fonctionnalité est très pratique et facilite l’affectation des matériaux et des masses, l’application des charges ou le post-traitement des résultats par éléments de la même famille.

C.3.9 Points de lecture des résultats et maillage

Les points de lecture des résultats découlent des vérifications à faire sur la structure. Les besoins de l’étude peuvent nécessiter plusieurs points de calcul des contraintes sur une même section (par exemple pour les contraintes normales et tangentielles).

Il ne faut pas confondre le maillage de calcul (c’est-à-dire l’ensemble des nœuds) et les points de lecture des résultats (parfois différents des nœuds).

Ce n’est pas parce qu’il y a beaucoup de points de lecture que le maillage est suffisamment précis.

Dans l'exemple ci-dessous, les multiples isolignes de moments transversaux, en particulier à proximité des appuis pourraient faire croire à une grande précision de calcul, alors que le maillage est trop large pour obtenir des résultats fiables.

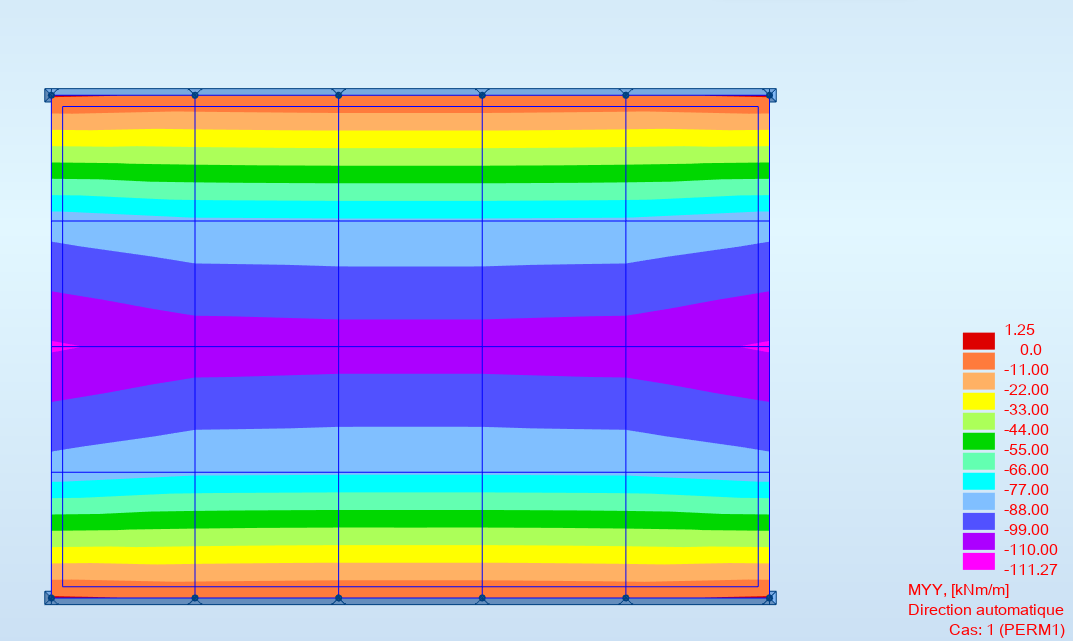
En effet, les points de lecture peuvent donner l’illusion d’un maillage raffiné alors que ce n’est pas le cas. Les résultats sur ces points de lecture étant interpolés des résultats aux nœuds.

En traçant les diagrammes de moment et de tranchant dans une coupe transversale, ceci apparaît clairement (la dalle est vue par le dessous):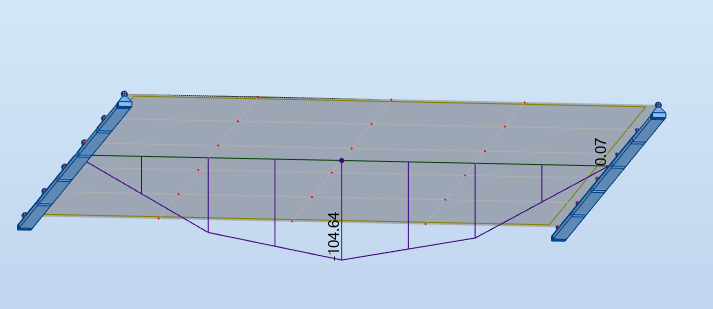

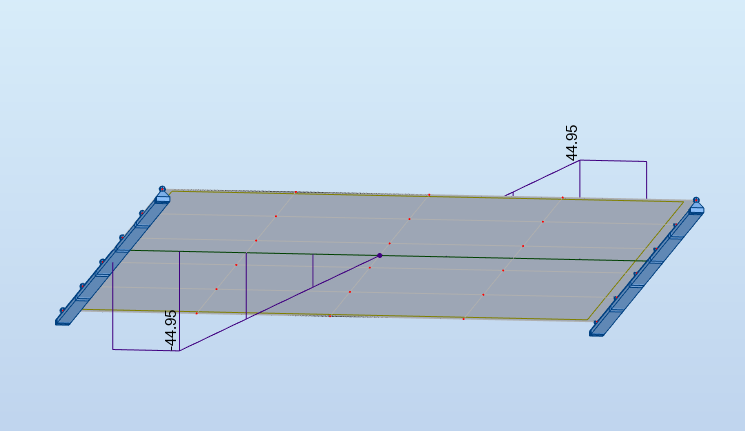
En raffinant le maillage, les graphes deviennent:

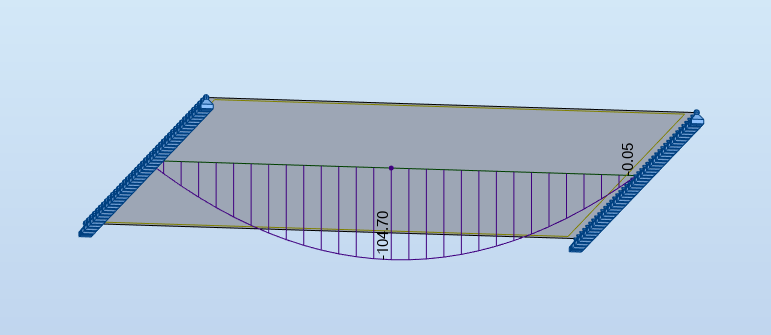
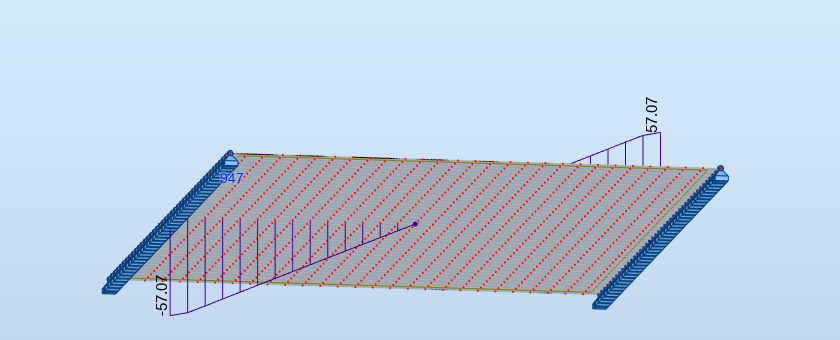
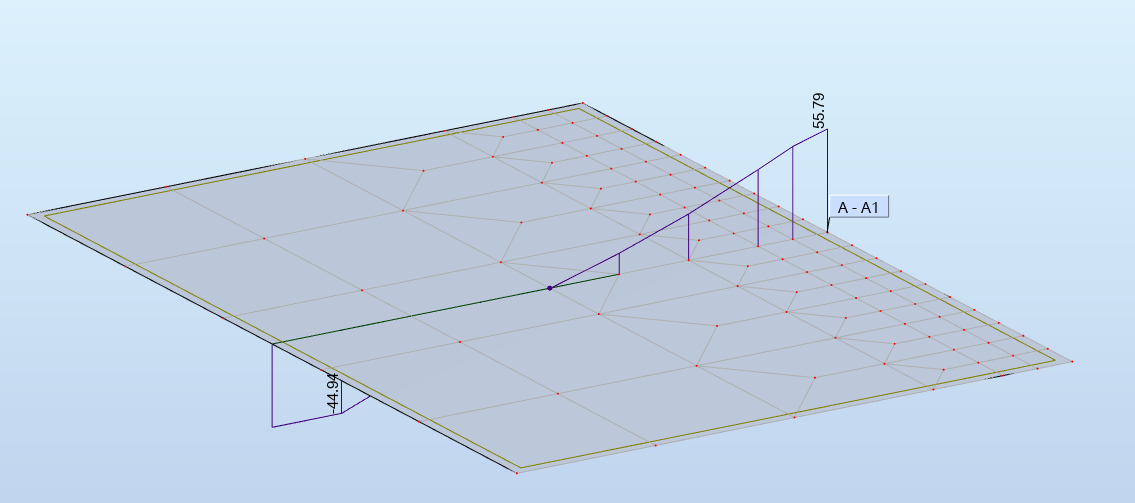
Dès lors qu'on a une singularité, ici la ligne d'appui, la taille du maillage intervient fortement dans la précision des résultats. Il suffit de raffiner le maillage pour s'en rendre compte:

Le calcul de l'intégrale des efforts montre un impact (sur cet exemple) fort sur le tranchant (écart de 22%) et très faible sur le moment, entre la zone de maillage grossier et la zone de maillage raffiné.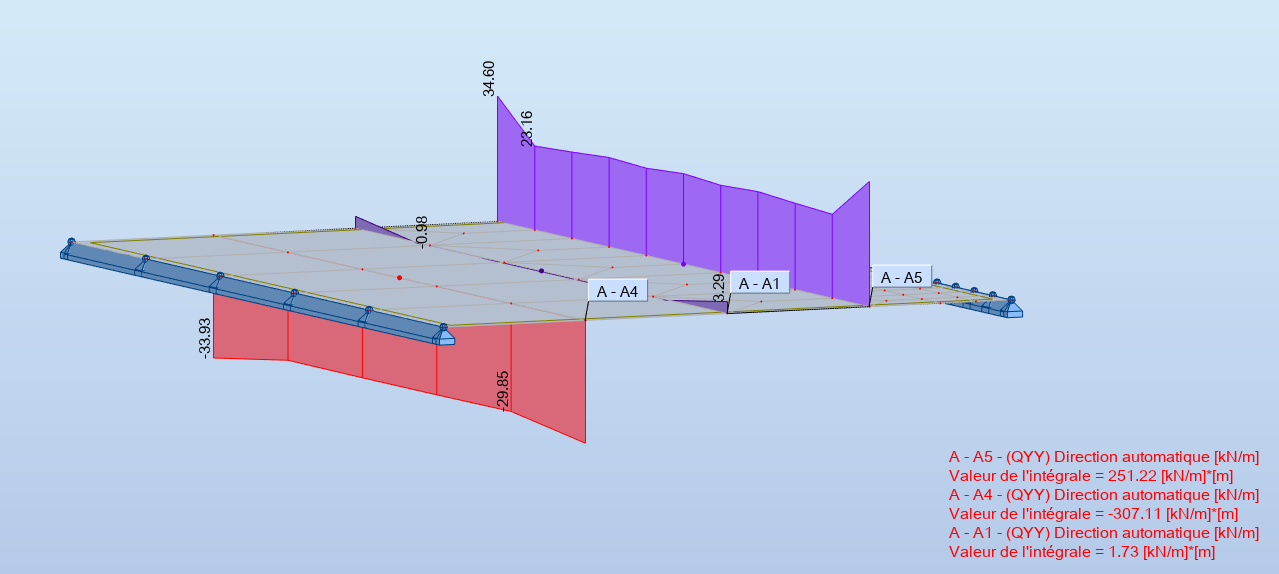



Intégrale de l'effort tranchant - plaque sur deux files d'appuis simples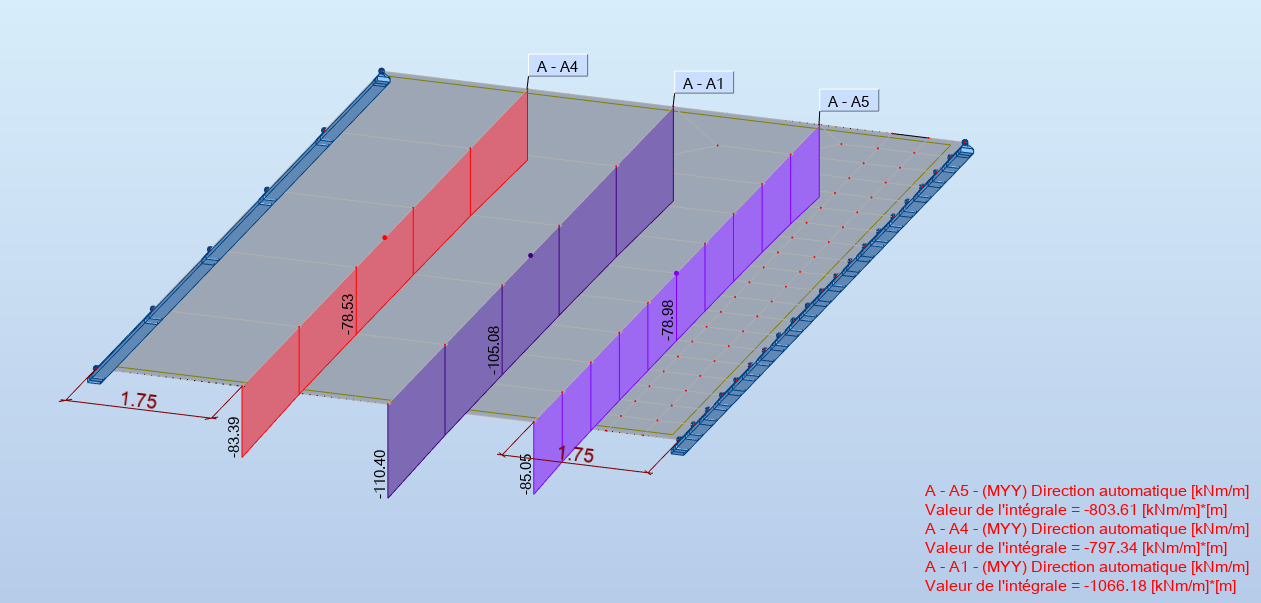



Intégrale du moment - plaque sur deux files d'appuis simples

Il suffit de créer une singularité pour le moment, en encastrant les rives, pour qu'un écart sur le moment se produise (de l'ordre de 17%)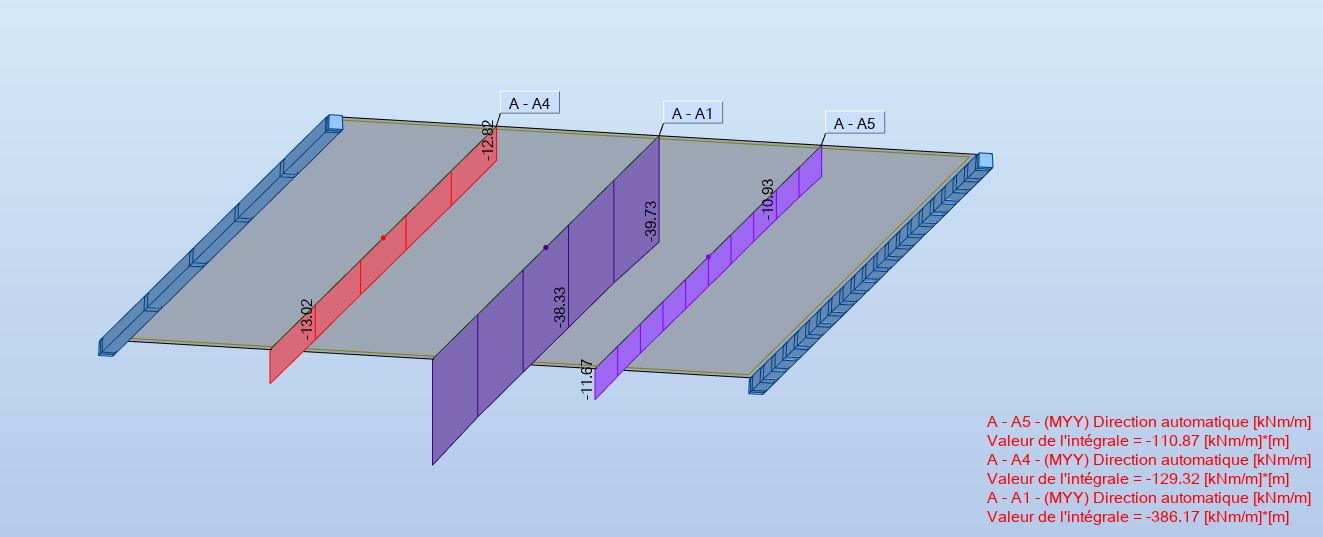



Intégrale du moment - plaque bi-encastrée