D.7 Compléments spécifiques pour les calculs dynamiques
D.7 Compléments spécifiques pour les calculs dynamiques
D.7.1 Vérification de la masse totale
Dans le cas d’études de type dynamique, l’un des paramètres fondamentaux est la masse de la structure qui sert à déterminer les fréquences propres de celle-ci.
Il est ainsi très important de s’assurer que l’intégralité de la masse de la structure est effectivement entrée dans le modèle. En effet, dans le cas où l’on utilise un modèle qui a déjà servi pour des calculs statiques, il peut arriver que certaines charges permanentes ou variables, telles que des équipements, aient été entrées en tant que charges (ponctuelles, linéaires, surfaciques, etc.) et non en tant que masse. Dès lors, il peut arriver que le programme ne considère pas ces charges comme masses mais uniquement comme des surcharges, et ne les prenne pas en compte dans son calcul de masse. Ceci risque de minorer les efforts sismiques.
Il convient donc de toujours s’assurer que la masse totale de la structure est bien celle recherchée. Cette information est en général accessible dans les résultats de l’analyse modale ou, encore mieux, peut être obtenue en effectuant trois calculs statiques, en appliquant un champ d’accélération unitaire dans les 3 directions (X,Y,Z) : seuls les éléments ayant une masse seront donc pris en compte, et la somme des réactions permettra donc de connaître la masse réellement prise en compte dans le modèle, dans chaque direction.
D.7.2 Vérification des masses participantes
Il convient de vérifier que l’analyse modale effectuée prend en compte suffisamment de modes propres. Pour cela, il faut vérifier que les masses modales participantes dans la direction étudiée et cumulées pour les différents modes calculés, représentent au moins 90% de la masse totale pouvant être mise en mouvement, calculée à partir des cas unitaires d’accélération, sans quoi les normes autorisent la prise en compte d’un pseudo mode (par direction).
Piège : Certains logiciels indiquent des % de masse modales cumulées qui peuvent être basés sur une mauvaise hypothèses de masse totale mobilisée : en effet, les parties de masses bloquées en déplacement par des appuis ne seront pas comptabilisées par le logiciel qui sur-évaluera de ce fait le % modal mobilisé. Une astuce pour pallier ceci est de définir des appuis élastiques avec une forte raideur plutôt que des appuis fixes : la masse totale sera alors exacte.
De manière générale, il est préférable de ne pas modéliser de masse associée à des appuis fixes.
Exemple de l’étude d’un modèle brochette avec 5 degrés de liberté :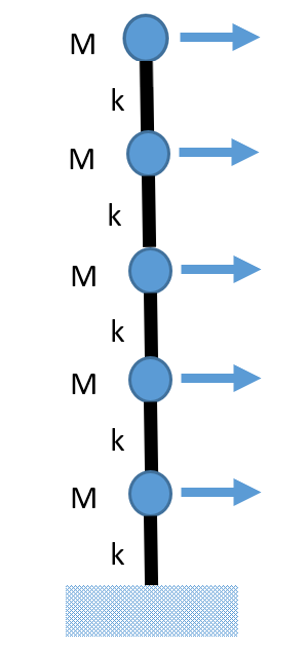
Trois cas sont étudiés :
-
Cas 1 : Masses et raideurs similaires à tous les niveaux ;
-
Cas 2 : Cas 1 mais avec une raideur 100 fois supérieure dans la hauteur du rez-de-chaussée ;
-
Cas 3 : Cas 1 mais avec une raideur 100 fois supérieure dans la hauteur des 2 premiers étages.
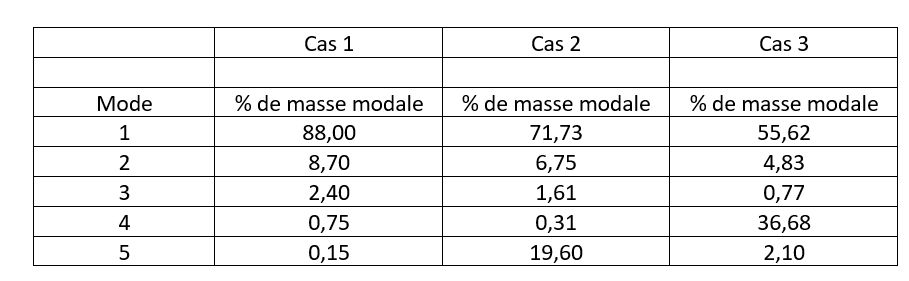
En supposant que toutes les périodes correspondent au plateau du spectre (valeur spectrale identique pour toutes les périodes) :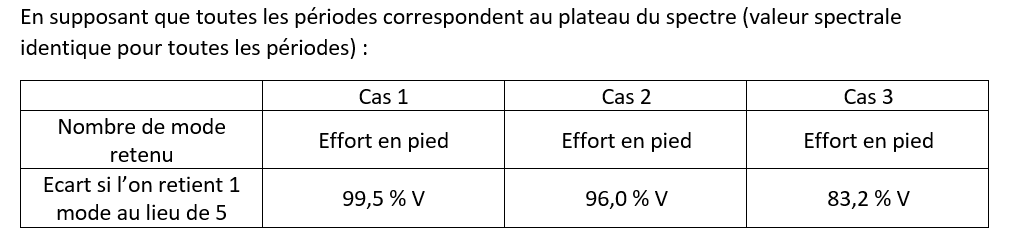
Il est donc important de prendre en compte tous les modes significatifs sinon les efforts de calculs pourraient être notablement sous-estimés.
Piège: Modes symétriques et antisymétriques.
Exemple de vibration d'une poutre
Suivant le type de calcul que l'on effectue, il ne faut pas considérer que les modes qui n'apportent pas de supplément de % de masse modale dans une direction donnée sont forcément sans intérêt.
Cas simple de la poutre sur deux appuis - les masses ne sont mobilisées que verticalement. Le tableau des résultats modaux montre que tous les modes pairs n'apportent pas de supplément de % de masse modale.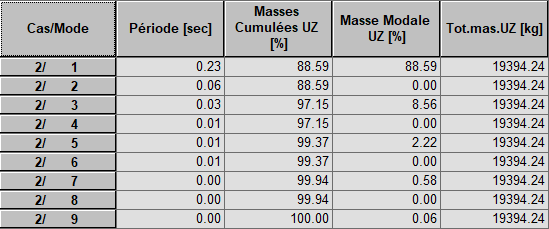
En examinant les déformées modales, on se rend compte que ce sont des modes ayant des déformées antisymétriques:
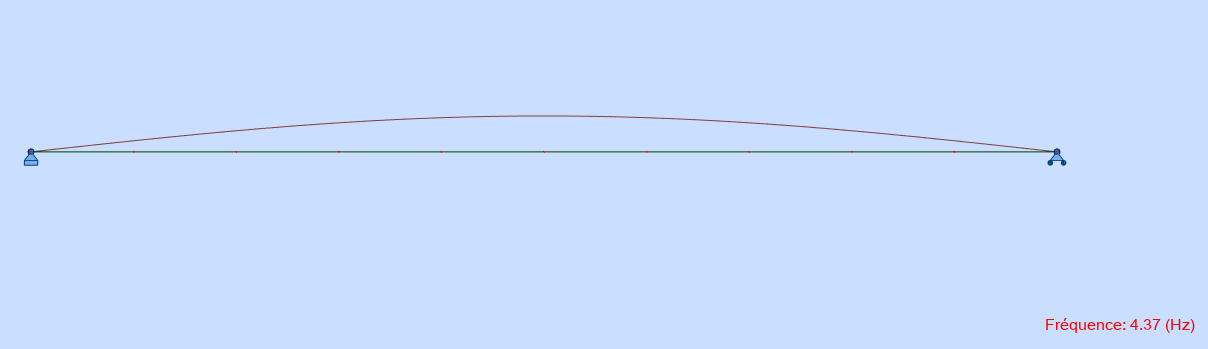
Déformée modale - mode 1
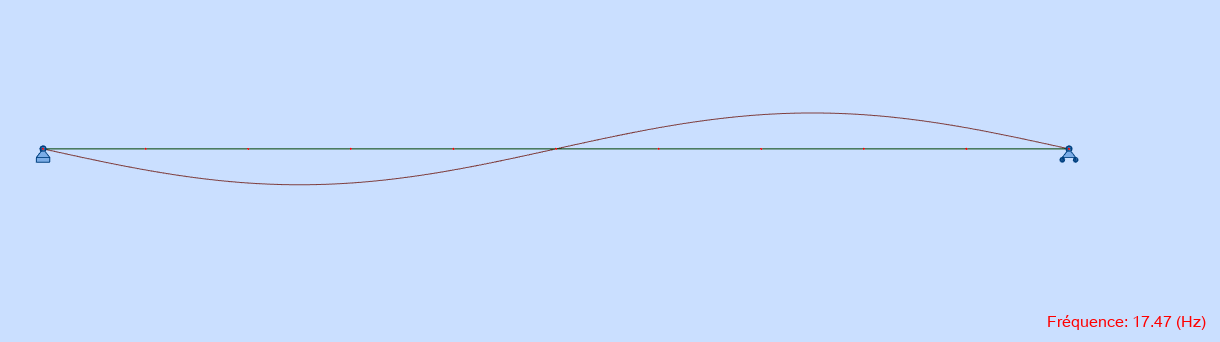
Déformée modale - mode 2
Dans le cas d'un calcul sismique spectral, ces modes n'apportent effectivement rien, par contre dans le cas d'un calcul de vibration d'une poutre ou d'une passerelle, ces modes ont tout leur intérêt. On admet effectivement que des piétons, dans leur mouvements peuvent avoir des actions en opposition et dans le sens la déformée modale. Un calcul harmonique est en effet effectué à partir des charges positionnées tel que ci-après: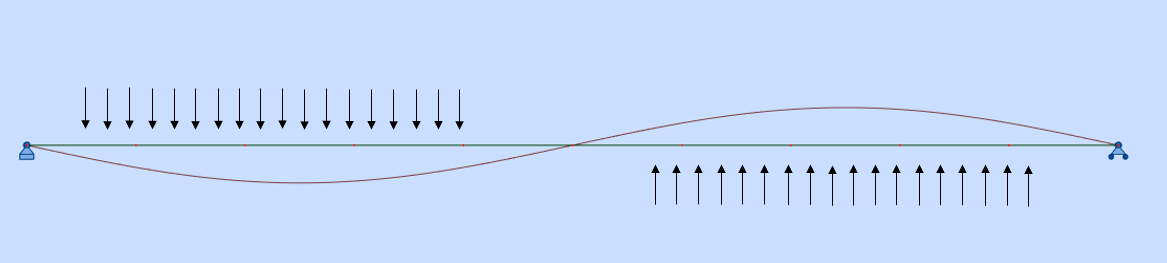
On se référera utilement au guide du Sétra/Cerema sur les passerelles piétonnes pour plus d'informations.
Analyse spectrale: enfin, on donne ci-dessous les efforts au nœud médian de cette poutre, calculée par une analyse sismique spectrale - on constate que les modes pairs n'amènent effectivement aucune contribution.
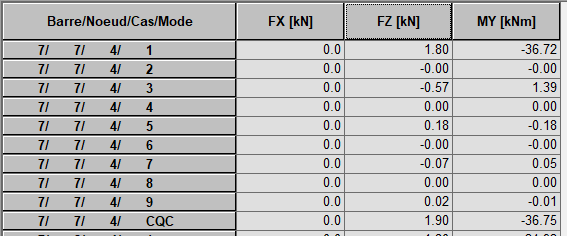
Piège: Modes de torsion
Exemple d'un bâtiment en torsion
Généralement, les bâtiments courants présentent un mode de torsion. Sur l’exemple ci-dessous, on peut observer :
-
Le 1er mode : avec un mode prépondérant selon UY (longitudinal),
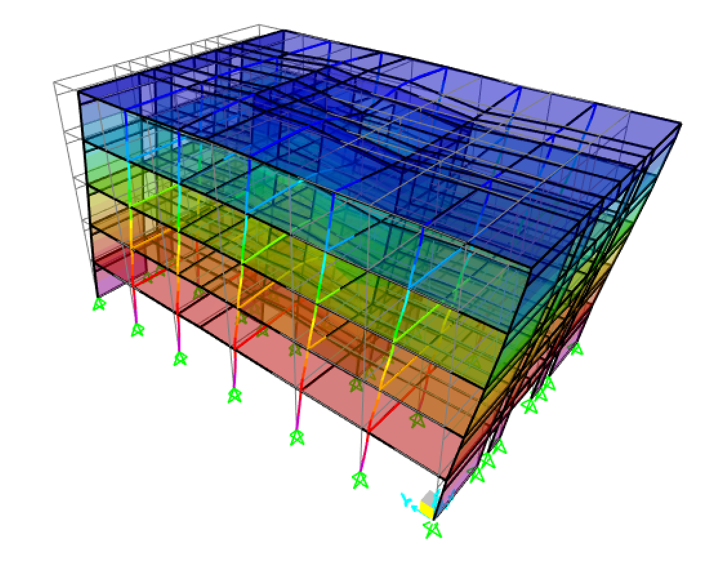
-
Le 2ème mode : avec un mode prépondérant selon UX (transversal),
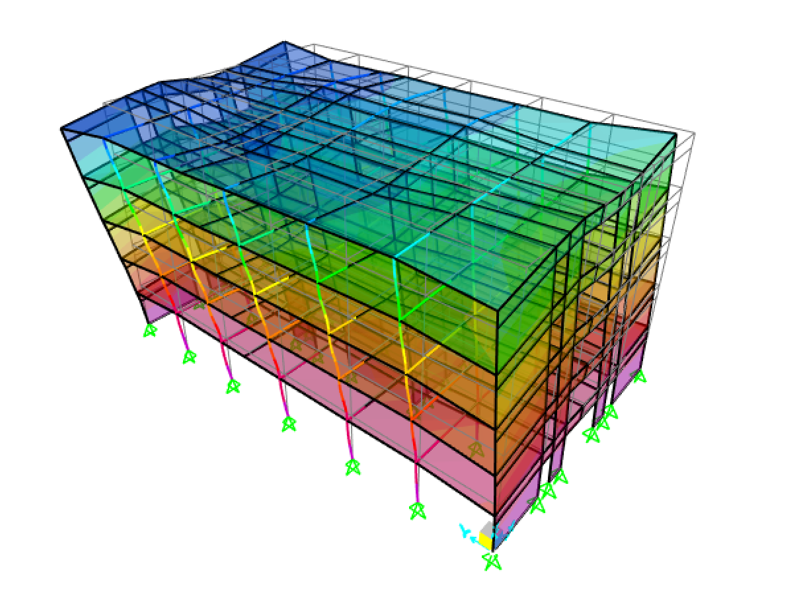
-
Le 3ème mode : avec peu de participation modale alors qu’il affecte notablement la structure. Il s'agit d'un mode de torsion.
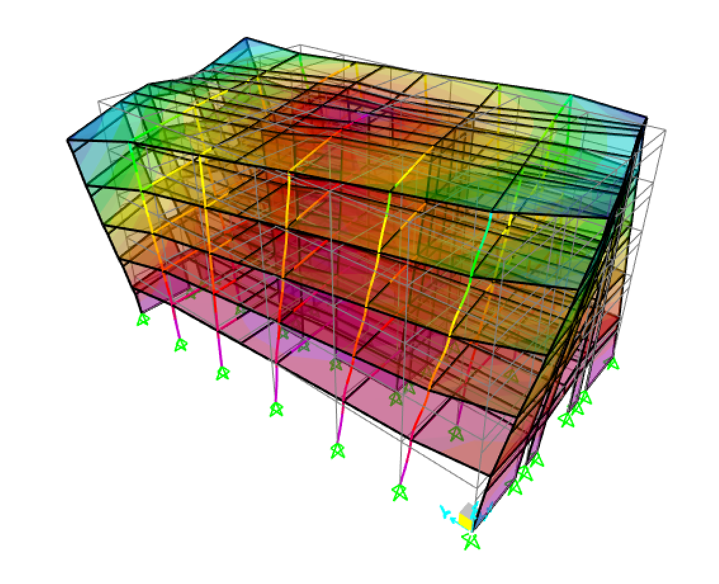

D.7.3 Vérification des principales fréquences propres
Afin de vérifier le comportement effectif de la structure en dynamique, il convient de s’assurer que les principales fréquences propres de la structure ont un ordre de grandeur cohérent.
Ces fréquences correspondent aux principaux modes de flexion, torsion, cisaillement, et elles correspondent en général aux modes ayant des facteurs de participation et des masses participantes importantes.
On notera néanmoins que se limiter aux modes ayant un facteur de participation important n’est pas un garant exhaustif des modes pouvant poser problème sous chargement dynamique. En effet, les facteurs de participation peuvent être calculés par les logiciels sur la base des déplacements modaux signés. Ainsi, il peut arriver que les facteurs de participation prenant en compte le cumul des valeurs renvoient des valeurs faibles alors que le mode est important.
Cela peut arriver par exemple pour une poutre continue sur trois appuis identiques et ayant deux portées identiques. Le principal mode de flexion de cette poutre correspond à la flexion d’une travée dans un sens et à la flexion de l’autre travée dans l’autre sens (forme de vague). Le facteur de participation de ce mode peut être très faible, les déplacements d’une travée contrebalançant les déplacements de l’autre travée dans le calcul, alors que ce mode est le principal mode de flexion de la structure, et peut être celui donnant la réponse en accélération la plus élevée si la structure est soumise à une excitation périodique.
Lorsque la structure est complexe, les formules de dynamique données dans la littérature ne permettent pas de retrouver précisément les valeurs de fréquence propre obtenues, puisque ces formules concernent des structures simples (fréquence propre d’une poutre isostatique sur deux appuis, d’une poutre en console, d’une poutre bi-encastrée ou d’un oscillateur à quelques degrés de libertés). Cependant, ces formules classiques permettent d’estimer les ordres de grandeur des principales fréquences propres en estimant de manière simplifiée le comportement de la structure pour se ramener à des fonctionnements simples pour les vérifications.
Dans le cas de structure de type poutre, on pourra ainsi estimer les fréquences propres de flexion à partir des formules classiques. Par exemple, et de manière très large, la fréquence propre de flexion d’une poutre sur deux appuis ayant une souplesse en rotation sera comprise entre la fréquence propre de flexion de la même poutre mais sur appuis rotulés et la fréquence propre de flexion de la même poutre sur appuis encastrés.
D.7.4 Calculs dynamiques sismiques modal/spectral
D.7.4.1 Vérification de la pertinence des premiers modes (instabilités, déplacements)
Les 2 ou 3 premiers modes globaux visualisent le fonctionnement de la structure, ce qui permet d’une part d’en comprendre le fonctionnement, d’autre part de repérer les problèmes de modélisation.
Pour un bâtiment bien dimensionné, les 2 premiers modes sont toujours selon X et Y, le troisième mode est un mode de torsion.
Pour les bâtiments courants, la période fondamentale est de l'ordre de 1/25 à 1/16 du nombre d'étages.
D.7.4.2 Vérification des axes globaux X et Y par rapport aux premiers modes
Il faut vérifier que les directions sismiques étudiées X et Y sont alignées selon les premiers modes importants. Dans le cas contraire, les calculs des CQC seront faussés.
Les solutions sont :
-
dans le cas d’un bâtiment, tourner le modèle selon les axes principaux
-
dans le cas d’un pont courbe, soit calculer le séisme sur un modèle droit, soit faire plusieurs calculs en variant les axes en fonction des biais des piles.
D.7.4.3 Validation du nombre de modes - Mode complémentaire
L’Eurocode 8 fixe un pourcentage minimum de masse à intéresser dans le calcul spectral.
Si l’on n’arrive pas à intéresser 90% de la masse, les logiciels permettent la prise en compte d’un mode complémentaire. C’est un mode fictif affecté de la masse non excitée par les modes étudiés et affecté de l’accélération spectrale associé au dernier mode étudié.
On a pu voir que négliger des modes fausse les résultats (cf. 1er exemple du D.7.2).
D.7.4.4 Calcul spectral et combinaisons CQC
Le calcul spectral permet d'obtenir les effets structurels (efforts, déplacements…) de chacun des modes. Puis, en fonction de la répartition statistique du séisme suivant les fréquences (définie par le spectre réglementaire), les effets sont combinés de manière à obtenir la réponse statistique de la structure à un séisme.
La combinaison des différents calculs modaux unitaires se fait selon le mode CQC ou SRSS, dont la définition théorique est fournie en Partie 1 – Chapitre 2.
Il convient de distinguer les spectres règlementaires utilisés en bâtiment (qui sont généralement des spectres de dimensionnement) et ceux utilisés pour les ponts (qui sont des spectres élastiques).
On passe du second au premier en divisant par un coefficient de comportement (égal ou supérieur à 1,5) qui tient compte des capacités de plastification de la structure. Les valeurs des coefficients de comportement sont définis par l'Eurocode 8.
Dans tous les calculs spectraux, il convient de veiller à bien définir l’amortissement de la structure. Selon les logiciels, on affecte l’amortissement aux modes ou aux matériaux. Dans le second cas, l’amortissement du mode dépendra de la participation de chaque matériau dans la déformée du mode considéré.
Attention, si l'on souhaite attribuer un amortissement dans les ressorts modélisant le sol, ceci correspond à une étude de type interaction sol-structure dynamique, et il n'est pas possible d'utiliser un spectre de dimensionnement mais uniquement un spectre élastique.
Enfin, comme indiqué en C16.8, un coefficient de comportement différent peut être affecté à chaque direction.
Après les combinaisons CQC ou SRSS (qui combinent les modes), il faut faire les combinaisons de Newmark (combinaisons de direction de séisme), puis les combinaisons d'actions.
D.7.4.5 Vérification des réactions d’appuis sous cas élémentaires
Il faut dans un premier temps faire le bilan des réactions d’appuis des cas sismiques élémentaires EX EY EZ et les comparer aux masses totales.
La vérification des réactions d’appuis ne peut se faire qu’en signant les modes.
Pour un bâtiment fondé sur radier ou sur semelles filantes, il est important de limiter les décollements des appuis, en effet le calcul élastique fait apparaitre des tractions dans les appuis qui n’existent pas dans la réalité car les fondations se soulèvent.
Les réactions d’appuis négatives (entourées en rouge) ne peuvent pas exister car les fondations se soulèvent dans la réalité, la répartition réelle des contraintes sur le sol est donc différente de celle calculée (cf. C16.8.3).
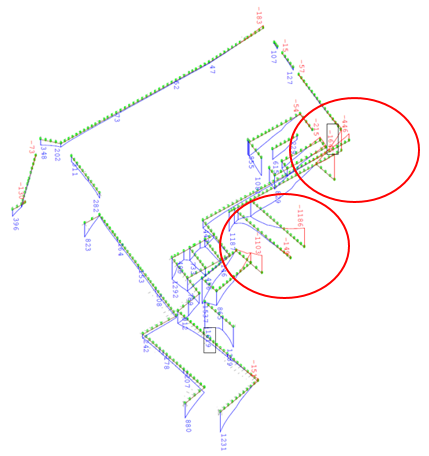
Réactions d’appuis d’un bâtiment sous fondations superficielles
Il est admis de considérer les modélisations « élastiques » représentatives si les soulèvements sont limités : la limite est prise égale à 30% dans le cas général (voire 10% dans le cas de bâtiment nucléaire)
Lorsque les décollements sont importants, il faut procéder à des calculs sismiques non-linéaires beaucoup plus complexes. Cette vérification de non soulèvement du bâtiment doit être réalisée avec soin :
-
il est nécessaire de signer les modes en fonction des modes principaux car les réactions d’appuis CQC sont toujours positives.
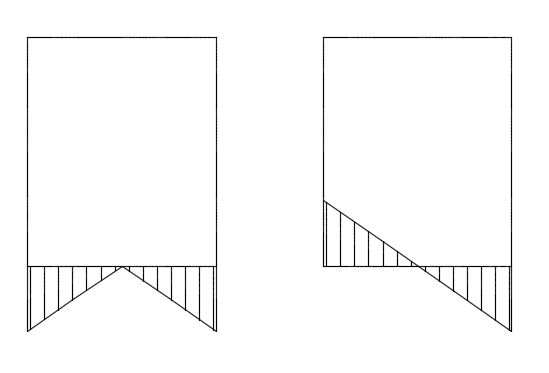
Réactions d’appuis CQC / Réactions d’appuis CQC signées
Les combinaisons sismiques (CP + E) n’ont aucun sens si les efforts sismiques E sont tous positifs, alors que les charges permanentes CP sont soit positives soit négatives.
-
Il est nécessaire d’étudier séparément toutes les combinaisons de Newmark
Exemple des 24 combinaisons de Newmark pour le bâti courant :
-
CP +/- 1.0 EX +/- 0.3 EY +/- 0.3 EZ
-
CP +/- 0.3 EX +/- 1.0 EY +/- 0.3 EZ
-
CP +/- 0.3 EX +/- 0.3 EY +/- 1.0 EZ
D.7.5 Calculs dynamiques autres que sismiques
Ce paragraphe concerne les calculs dynamiques autres que des calculs modaux spectraux (par exemple vibration d’un ouvrage ferroviaire ou d’une passerelle piétonne en vue de vérifier des critères de confort), et correspond à des calculs dans lesquels le chargement et la structure sont calculés avec une évolution dans le temps.
D.7.5.1 Vérification du comportement en vibrations libres ou à la résonance
Dans le cas d’une étude de confort d’un ouvrage ferroviaire ou d’une passerelle, il convient de rechercher les cas de charges pouvant provoquer une mise en résonance de la structure et les conséquences d’une telle mise en résonance. Pour cela, il est donc nécessaire d’appliquer des chargements périodiques pouvant provoquer ces mises en résonances.
Pour rappel, la résonance de la structure intervient quand le chargement périodique est à une fréquence identique à l’une des fréquences propres de la structure.
Pour vérifier que les fréquences des chargements périodiques appliqués sont cohérentes avec celles de la structure, on peut aisément les retrouver sur les graphiques temporels obtenus a posteriori. Cette méthode s’applique sur l’évolution temporelle de l’accélération, de la vitesse ou du déplacement d’un nœud représentatif (par exemple le milieu d’une poutre).
Pour cela, il suffit d’effectuer un décompte du nombre de périodes entre deux points éloignés dans le temps et de diviser ce nombre par le temps séparant ces deux points. Cela donne une assez bonne approximation de la fréquence de vibration du nœud en question:
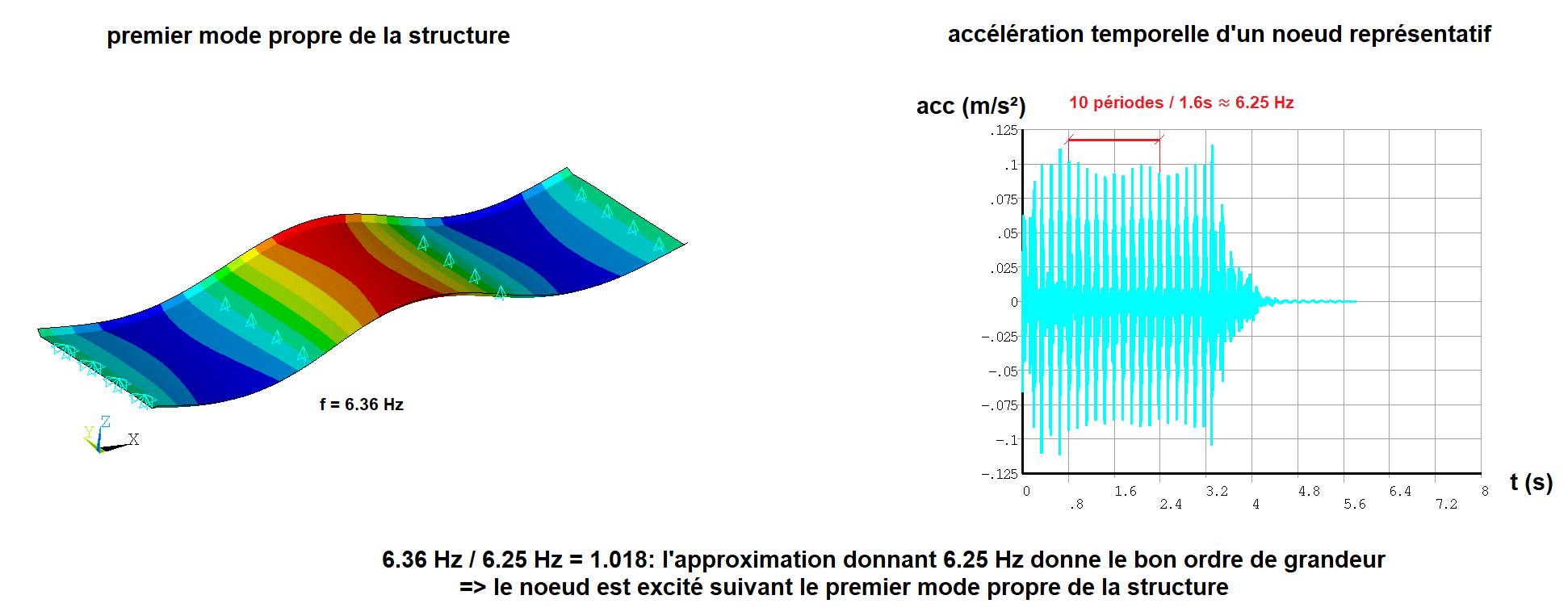
Si la courbe présente une variation périodique très marquée sur la période de temps où le chargement est appliqué, cela correspond à une vibration forcée de la structure, et la méthode décrite précédemment permet de s’assurer que la fréquence du chargement est bien celle attendue.
Si la courbe présente cette variation périodique sur un laps de temps postérieur au chargement (le calcul a été continué après avoir cessé d’appliquer le chargement), cela correspond aux vibrations libres de la structure. La méthode décrite précédemment permet, dans ce cas d’estimer, la principale fréquence propre de la structure et donc de s’assurer que le mode propre excité est bien le bon.
Pas de commentaires