C.10 Comportement spécifique au cisaillement et à la torsion
C.10 Comportement spécifique au cisaillement et à la torsion
De manière générale, il convient de noter que les modélisations filaires ne prennent pas systématiquement en compte les déformations d'effort tranchant, ni de manière appropriée les déformations de torsion.
Toutefois, dans le cas d'une modélisation d'une structure sensible sur ce point, il faut veiller à activer l'option de prise en compte des déformations d’effort tranchant et de torsion et à bien définir les sections réduites et inerties de torsion.
On peut noter également que les phénomènes de torsion gênée sont impossibles à modéliser en filaire, car les éléments poutres de RDM sont bâtis sur une hypothèse de conservation des sections droites (sans distorsion ni gauchissement) et pourtant, leur prise en compte conduit à des distribution de contraintes différentes de celles calculées en RDM “classique”.
La prise en compte de la torsion gênée demandera en général la modélisation séparée de tous les plaques constituant le profil mince de la section.
Quelques exemples de structures sensibles à ces phénomènes :
-
pour le tranchant : poutres PRS élancées (poutres de bipoutres mixtes, par exemple), structure de type console (voiles de contreventement avec un ratio hauteur/longueur faible). La non prise en compte de la déformation de tranchant aboutira, dans le premier cas, à des déformées sous-évaluées conduisant à une contreflèche erronée et, dans le second cas, à des raideurs sur-évaluées ;
-
pour la torsion : structures non libres de se distordre (en un ou plusieurs points).
Comparaison de calculs de l’angle de rotation d’une poutre en console en I
Données - poutre en console :
-
Conditions aux limites : encastrée en x=0 (θ=0, θ'=0) et libre en x=L (B=0, T=0)
-
Longueur : L = 1 m
-
Chargement : moment de torsion à l’extrémité x=L : Mx = 10 kN.m
-
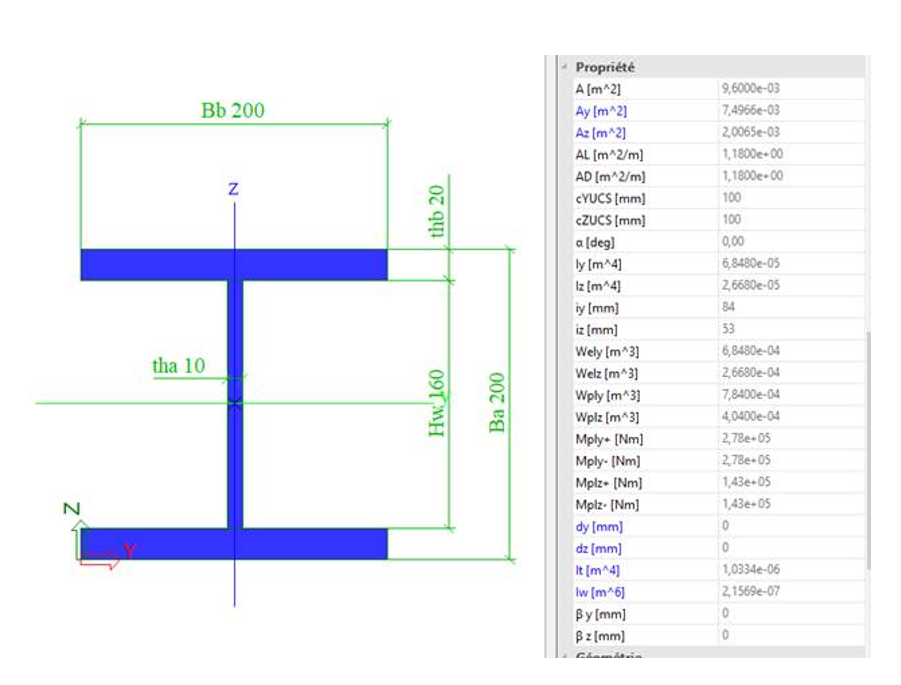
Section : PRS ht = 200 mm, bt = 200 mm, tf = 20 mm, tw = 10 mm
Modèle éléments plaques
Chargement :
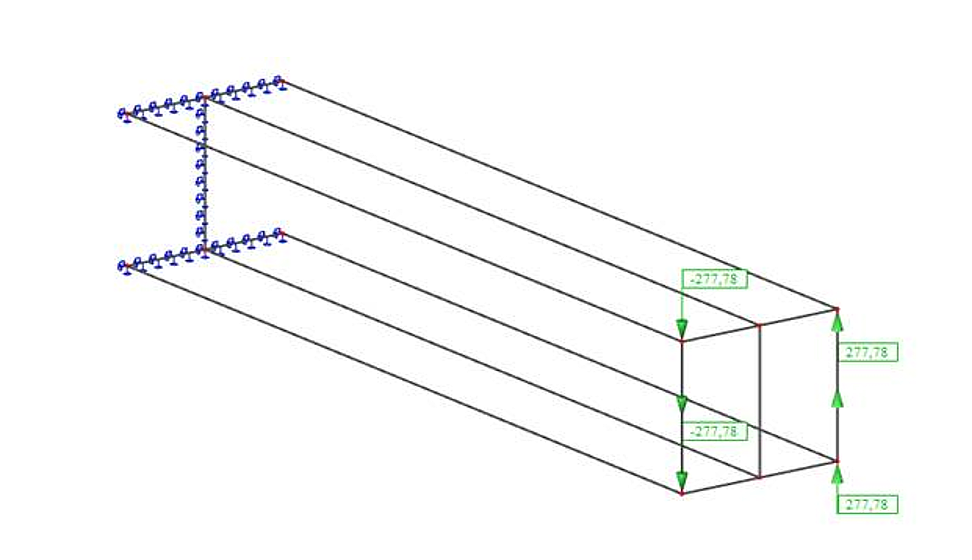
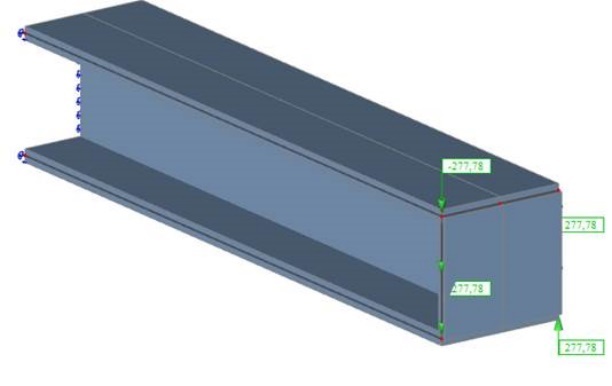
Résultante: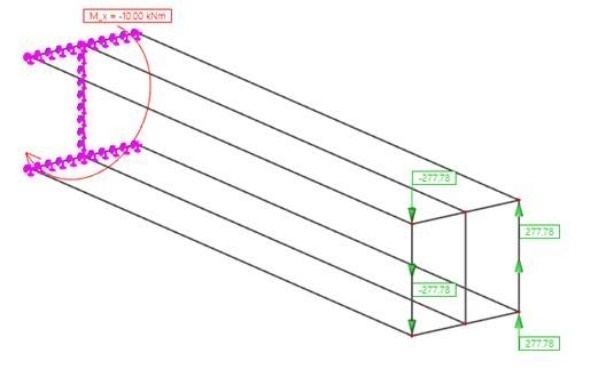
Déplacement θ(L)=0.042 rad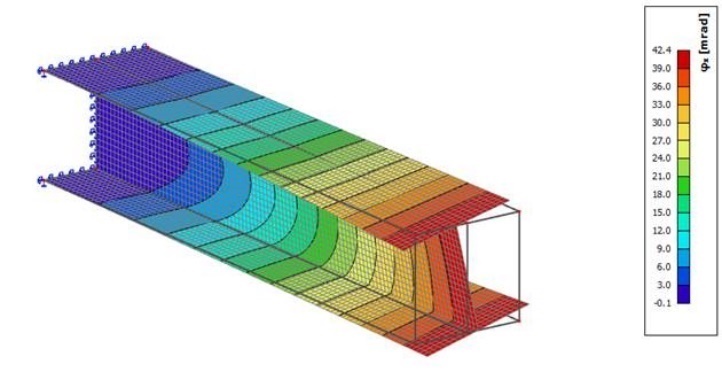
Modèle élément filaire
Chargement :
Résultante: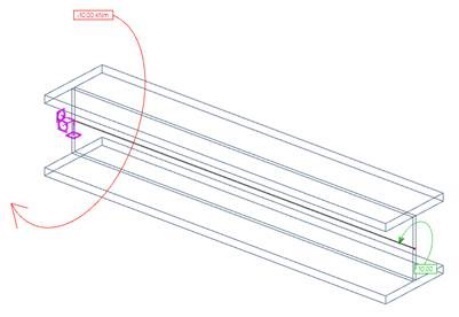
Déplacement θ(L)=0.1198 rad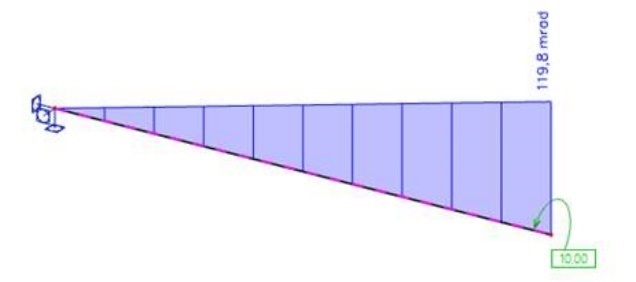
Calcul analytique
L’équation différentielle de l’angle de rotation est donnée par :
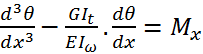
Avec les conditions aux limites donnée au paragraphe précédent, la solution de cette équation est :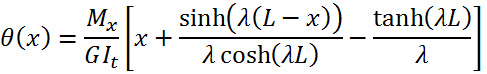
Avec :
-
It : inertie de torsion de St Venant
-
Iω : inertie sectorielle
-
Mx : moment de torsion
-
L : longueur de la poutre
-
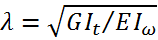
Application :
-
L = 1 m
-
G = 80 770 MPa
-
E = 210 000 MPa
-
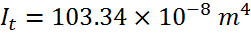(calculé par le logiciel) -
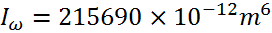(calculé par le logiciel) -
Mx = 10 kN.m
-
Le calcul analytique et le modèle éléments surfaciques donnent le même résultat de rotation θ(L)=0.042 rad.
Le calcul de modèle élément filaire donne un résultat 2.85 fois supérieur.
Dans le modèle élément filaire , la raideur due à l’inertie de gauchissement n’est pas prise en compte pour le calcul de l’angle de rotation :
Conclusion
En règle générale, pour les modèles en élément filaire, les raideurs dues à la torsion d’une poutre en section ouverte ne sont pas bien prises en compte dans les calculs.
En cas de doute, une approche par éléments de type coque, sur un modèle simplifié, global ou local peut aider à cerner les effets.
Pas de commentaires