C.5 Conditions aux limites

C.5 Conditions aux limites

C.5.1 Cas général

Les conditions aux limites sont déterminées par les degrés de liberté bloqués ou non des nœuds situés aux frontières de la structure (supports de la structure, coupures …).

Les notions de repères et de conditions aux limites sont étroitement liées ici. L’orientation d’une condition aux limites (forces, moments, déplacements imposés, accélération…) va dépendre de celle du repère actif au moment de sa mise en place et/ou de celle de l’entité (nœud, élément) sur laquelle elle vient s’appliquer.

Pour les repères, il a lieu de distinguer les repères liés aux éléments et les repères liés aux nœuds.

Généralement, par défaut, les repères liés aux nœuds sont identiques au repère global. On peut cependant attribuer à un ou plusieurs nœuds un repère d’orientation différent afin de pouvoir appliquer en ce(s) nœud(s) une condition aux limites suivant une orientation particulière. De simples contrôles graphiques de l’orientation de charges nodales (forces, moments, déplacements imposés) permettent de visualiser la bonne définition de ces repères nodaux.

Pour les éléments, les repères locaux sont liés généralement aux orientations principales définies lors de la création de l’élément. De simples contrôles graphiques de l’orientation des charges appliquées sur les éléments (pression par exemple) permettent de visualiser la bonne définition de ces repères éléments.

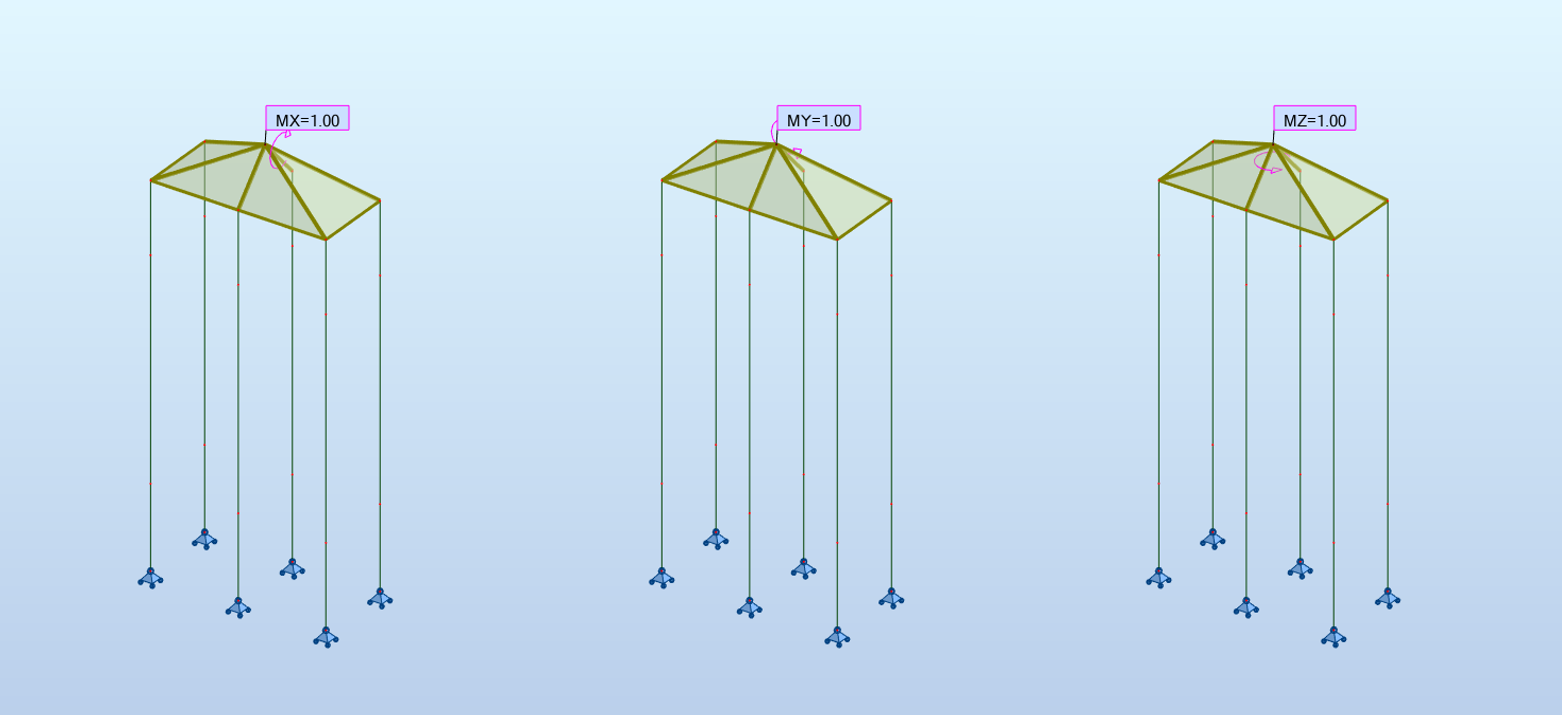
Les conditions aux limites doivent assurer la stabilité de la structure vis-à-vis des chargements qui lui sont appliqués et être représentatives de son fonctionnement global. Cette stabilité doit être effective systématiquement dans les 6 composantes globales X, Y, Z, RX, RY et RZ, même si les chargements ne concernent que quelques directions.

La stabilité suivant une translation s’effectue toujours par le blocage d’au moins un nœud suivant la direction de cette translation.

La stabilité autour d’un axe s’effectue soit par le blocage en rotation d’un nœud (suivant l’axe de rotation) soit par le blocage en translation de deux nœuds disposés dans un plan perpendiculaire à la rotation.

Il est important de vérifier que les réactions dans les directions bloquées uniquement pour des questions de stabilité numérique sont nulles.

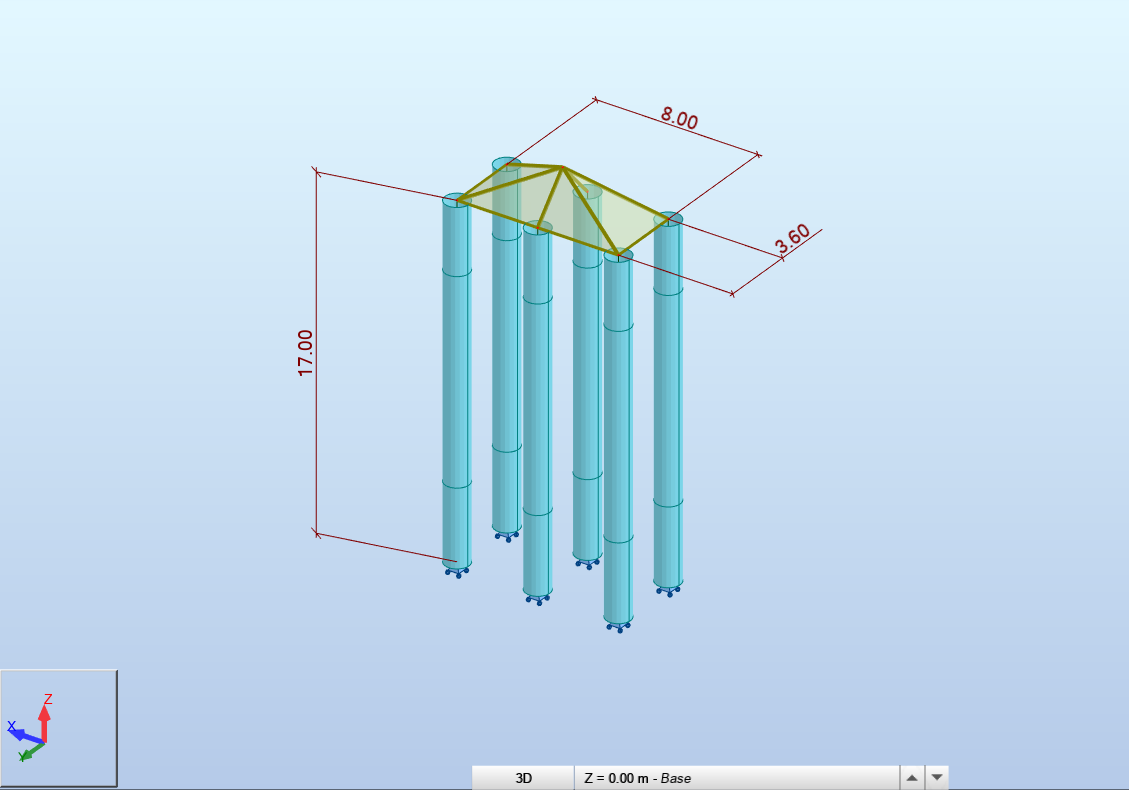
Illustration :

Objectif : descente de charge d’une dalle appuyée sur 4 poteaux ;

Bilan :

On vérifiera qu’aux nœuds bloqués suivant UX et UY, les réactions RX et RY sont nulles.

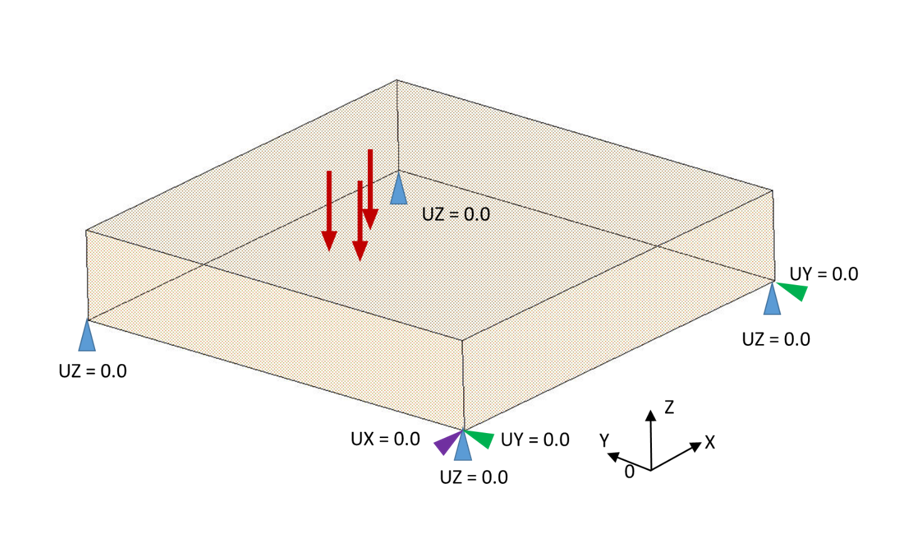
Exemple pour la stabilité minimale d’une dalle chargée en Z

Piège : la dalle n’est chargée qu’en Z, mais pour assurer la stabilité du calcul, il faut empêcher ses déplacements en translation en X et Y et en rotation autour de Z. Dans le cas présent, cela a été effectué en bloquant 2 points en Y et 1 point en X. (NB : la stabilité en Z nécessite un minimum de 3 points non alignés bloqués en Z).

Dans un modèle en 3 dimensions, un encastrement signifie que les 3 rotations et les 3 translations sont bloquées.

Dans la pratique, le logiciel peut procéder de deux façons pour le blocage des déplacements, sans laisser le choix à l’utilisateur :

Il est important de comprendre comment le logiciel procède pour pouvoir détecter d’éventuelles instabilités numériques qui peuvent conduire à un arrêt des calculs ou des résultats non équilibrés.

C.5.2 Modélisation de différents types d’appuis

Les appuis peuvent souvent être considérés comme fixes sauf lorsque le sol intervient dans le comportement de la structure c’est-à-dire lorsqu’il existe une interaction, statique ou dynamique, entre le sol et la structure (ISS) : par exemple un sol mou générant des tassements différentiels d’appuis ou pour cerner le comportement sismique.

Les structures sont fondées sur trois types de fondations : superficielles (semelles isolées ou filantes), radiers ou fondations profondes (pieux, puits, barrettes, inclusions rigides, …).

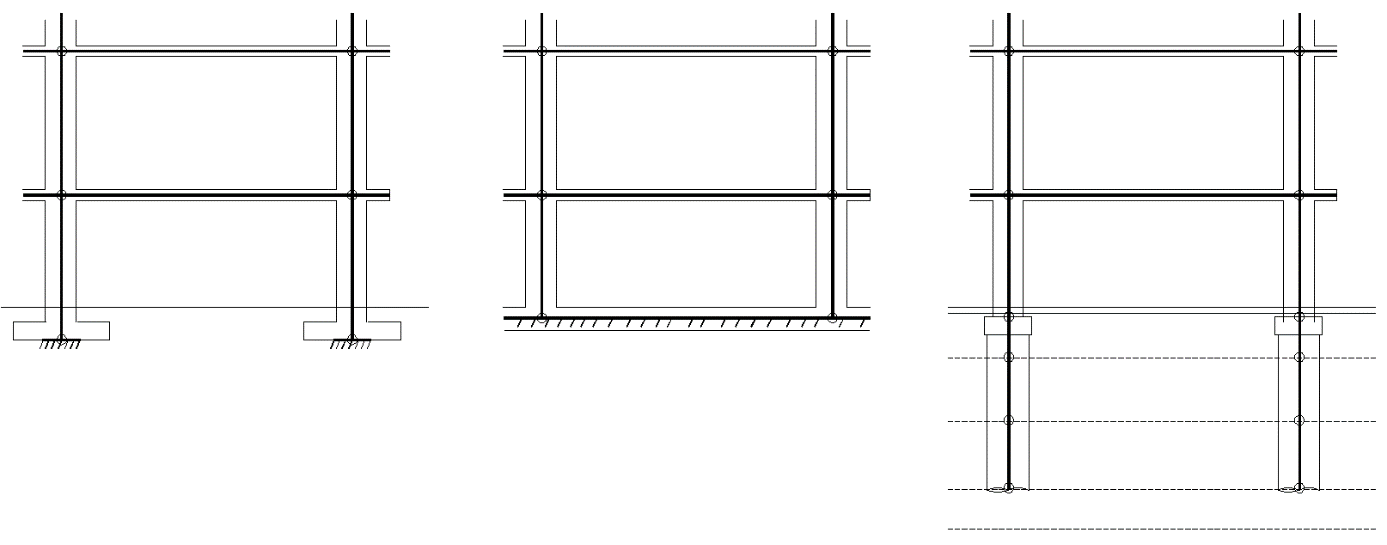
Illustration des fondations superficielles, fondations sur radier et fondations profondes.

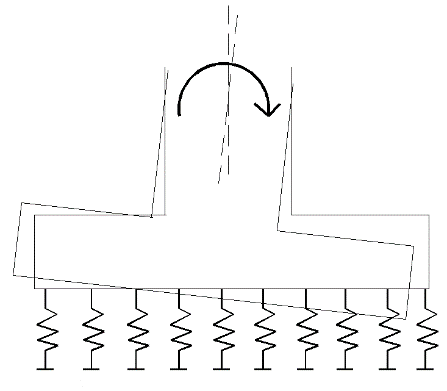
C.5.2.1 Fondations superficielles – cas des appuis sous poteaux

Les semelles superficielles sont modélisées par des appuis ponctuels selon 3 possibilités :

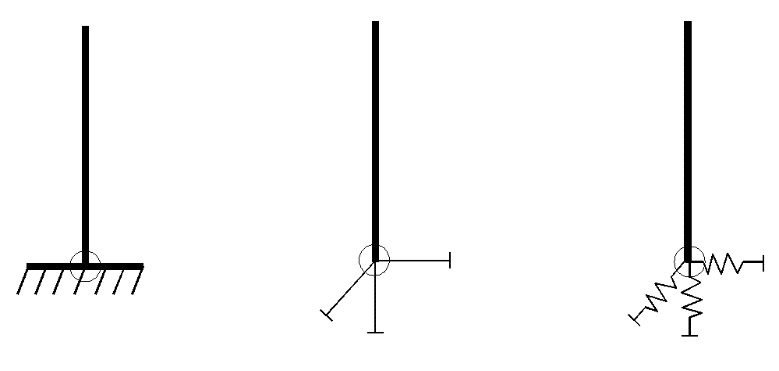
Illustration: appui encastré, appui articulé et appui élastique

Appui encastré : les 6 degrés de liberté sont bloqués.

Appui articulé : les déplacements sont bloqués et les rotations sont libres.

Appui élastique : l’appui est défini par 6 ressorts élastiques (un par degré de liberté) ou une matrice de raideur ou d’impédance.

Raideurs des appuis élastiques

Pour calibrer la raideur des appuis élastiques, il faut disposer de la raideur à l’interface entre la semelle et le sol. Cette raideur à l’interface (notée usuellement kv) est issue du rapport géotechnique.

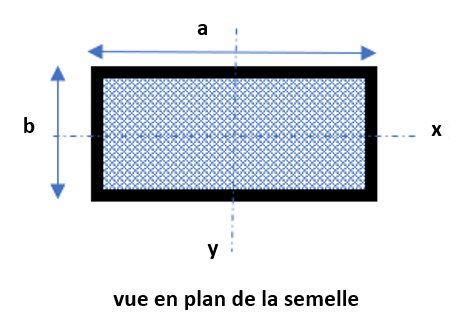
Le terme K_z (raideur statique du ressort vis-à-vis d’un effort vertical) s’obtient par la formule K_z = k_v x S où S est la surface de la semelle.

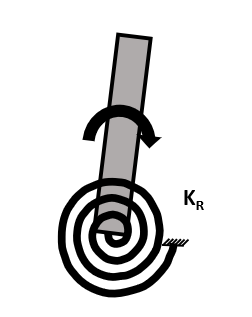
Les termes K_R s’obtiennent par la formule K_Ri (en N.m/rad) = I_i x k_v où I_i est l’inertie (en plan) autour de l’axe i de rotation de la semelle concernée.

Pour un rectangle, on va retrouver les termes Iy=b.a³/12 et Ix=a.b³/12, a et b étant les dimensions en plan.

On sera vigilant à la notion de raideurs à long terme, à court terme et sismique fournies par le géotechnicien, qui diffèrent notablement.

C.5.2.2 Fondations superficielles – cas des appuis sous voiles

Les voiles sont généralement modélisés par des éléments de plaques ou coques. Deux modes de modélisation sont possibles pour l’appui.

Méthode 1 : En définissant des appuis linéiques répartis sous le voile. Ce cas se rapproche soit de celui des poteaux (voir ci-avant) en répartissant les raideurs ponctuelles linéairement sur le voile, soit de celui des radiers (voir §5.2.3 ci-après), mais en considérant une seule direction de calcul.

Méthode 2 : En modélisant un appui central unique pour récupérer un torseur global en pied de voile pour le dimensionnement des fondations. Une barre rigide à la base du voile est alors nécessaire pour répartir les efforts dans le voile. Les conditions d’appuis sont identiques à celles des poteaux (encastrés ou élastiques ou avec raideurs).

Dans les deux cas, il convient de vérifier les unités pour la raideur introduite, en cohérence avec les unités physiques fournies par le géotechnicien : s’agit-il de N/m, N/m², N/m³ ? De même de N.m/rad ou N.m/deg ? (ou unités dérivées : kN, MN…)

C.5.2.3 Fondations sur radier

L’appui du radier sur le sol est modélisé par la mise en place de ressorts sous les différents nœuds du radier. Les raideurs des ressorts sont alors calculées selon le même principe que pour les semelles isolées. Elles peuvent être différenciées en fonction des zones de chargement. Attention à ce que la raideur soit bien proportionnelle à la surface afférente au nœud (difficulté possible en cas de maillage irrégulier, si cette affectation n'est pas automatisée dans le logiciel).

Certains logiciels proposent aussi des ressorts « surfaciques » sur plaque. Dans tous ces cas, vérifier sur un cas unitaire la bonne concordance entre effort et déplacement.

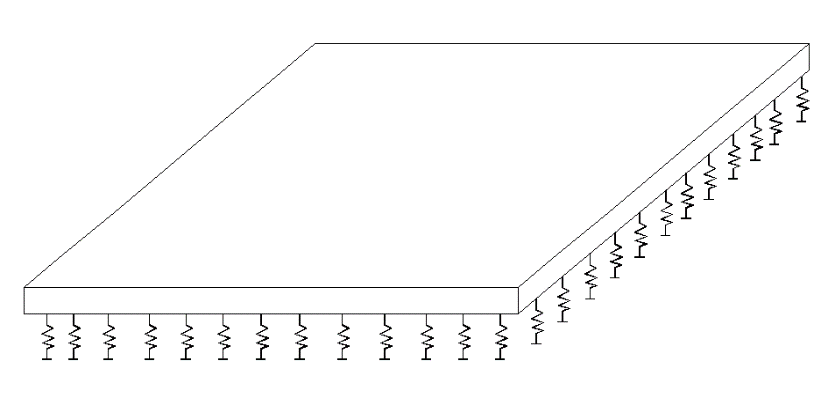
Modélisation du sol par un système de ressorts

Dans la réalité, la stabilité horizontale du radier est assurée par le frottement sous le radier et une éventuelle butée latérale. Dans la modélisation, on choisira soit des ressorts horizontaux surfaciques sous le radier, soit des ressorts sur le pourtour (ponctuels ou répartis), en fonction des vérifications internes à mener.

Attention: pour les modélisations avec ressorts surfaciques horizontaux, la raideur horizontale est en fait liée au frottement radier/sol avec des glissements éventuels. Dans le cas d’une étude de retrait, une surestimation sur cette raideur horizontale vient brider artificiellement le radier et peut générer des contraintes de traction importantes et non réalistes.

C.5.2.4 Fondations sur pieux

Les fondations sur pieux peuvent être modélisées selon 3 méthodes.

Méthode 1 : chaque pieu est modélisé au moyen d’une poutre sur sol élastique (ou appuis linéiques élastiques). les raideurs horizontales du sol dépendant des caractéristiques des couches de sol (Kx et Ky) sont généralement déterminées par le géotechnicien (attention au maillage et à la concordance des unités). Un appui vertical est positionné à la base du pieu pour représenter la raideur en pointe.

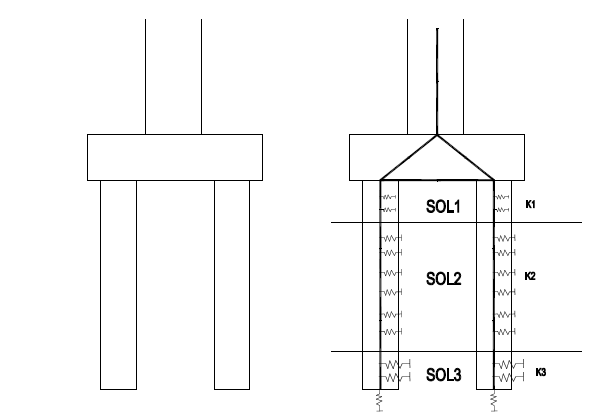
Méthode 2 (intermédiaire mais peu usitée) : chaque pieu est modélisé par un appui (ou matrice) élastique caractérisé par 6 raideurs qui sont généralement calculées par le géotechnicien.

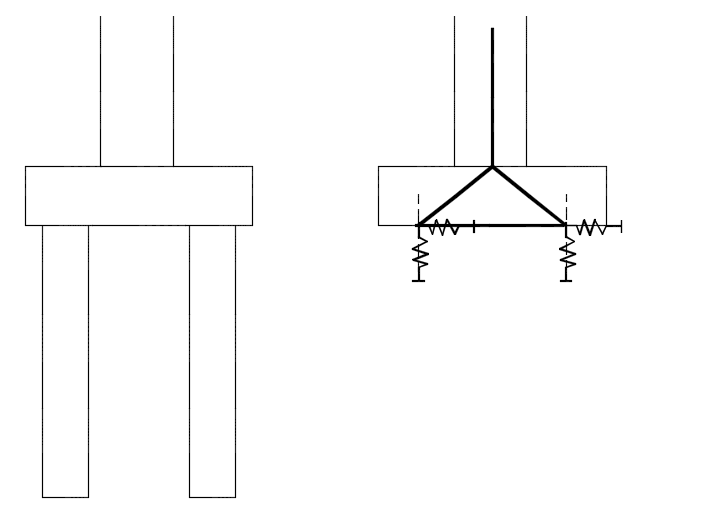
Méthode 3 : Il est possible de remplacer une fondation complexe par sa matrice de raideur ou de souplesse, qui intègre la configuration globale de la semelle avec l’ensemble des pieux.

La fondation sera modélisée dans le modèle général par un appui élastique au nœud A, dont les 6 raideurs auront été calculées au préalable à partir d’un modèle local des fondations. Voir l'exemple de calcul ci-dessous.

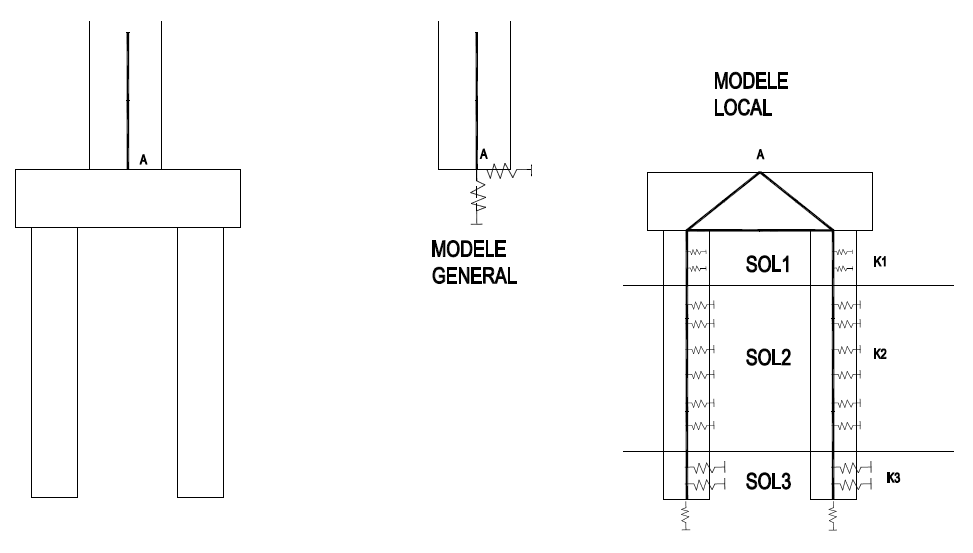
Du fait du couplage entre les déplacements horizontaux et les rotations dans les systèmes de fondations profondes, rien ne permet a priori de négliger les termes croisés (non diagonaux) de la matrice de raideur. Or très peu de logiciels permettent la prise en compte de la totalité de la matrice ; ce qui est un problème. Il convient de démontrer au cas par cas que la « diagonalisation » de la matrice n’a pas d’impact notable sur les efforts et déplacements de la structure.

Les méthodes 2 et 3 permettent de limiter la taille du modèle, surtout dans le cas de nombreux pieux. En revanche la première méthode donne directement les efforts dans les pieux.

Plus généralement, dans les modèles globaux, on modélise les pieux ou groupes de pieux par des ressorts (méthode 3). Ce n’est que pour le dimensionnement des pieux eux-mêmes qu’on peut être amenés à les modéliser par des poutres verticales avec ressorts (méthode 1). On peut également utiliser des logiciels spécifiques.

Dans tous les cas, il ne faut pas oublier d’intégrer dans les coefficients Kx ou Ky l’ensemble des exigences réglementaires comme l’effet de groupe.

Enfin, dans le cas où les pieux sont calculés par une autre entité que celle en charge du modèle de la superstructure, des itérations peuvent être nécessaires pour arriver à une convergence des efforts.

Exemple de calcul d'une matrice de raideur.

Données : pieux de diamètre 1.20 m, Ebéton= 30000 MPa, Ksol= 6495 (kN/m)/m, hauteur de semelle 2.00 m.

Géométrie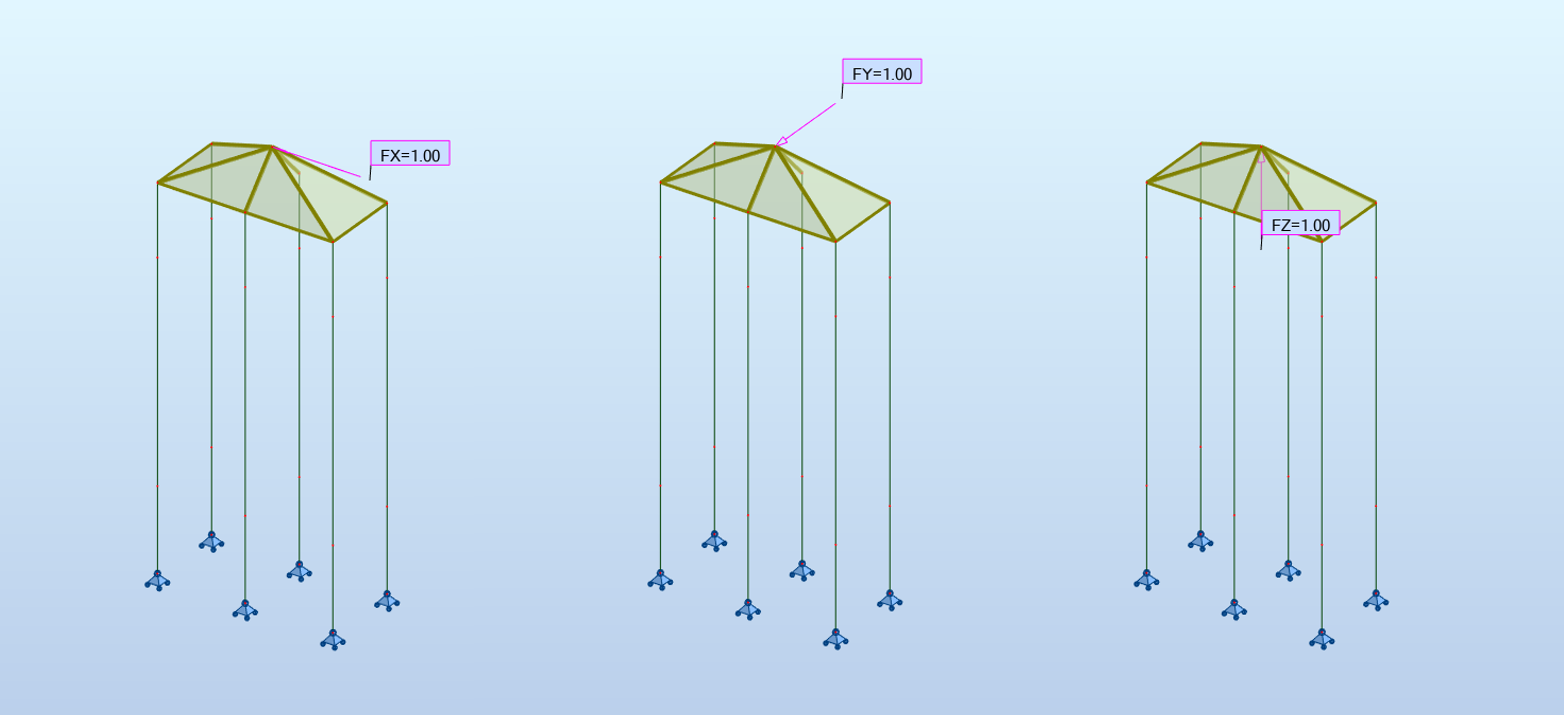

Efforts unitaires (1 kN ou 1 kN.m) introduits

Résultats:
Déplacements sous ces efforts = la matrice de souplesse [S]

Matrice de raideur [K]=[S]^-1 - (unités : KN, KN.m, m et rad)

(Les matrices s'inversent très simplement à l'aide d'un tableur).

Incidence de la non prise en compte des termes croisés : on ajoute une pile de hauteur 10 m et de section 5.00×1.00 m², E=32000 MPa au modèle précédent. La même pile est modélisée avec un encastrement élastique à 6 composantes qui sont les termes de la diagonale de la matrice ci-dessus. On applique un effort de 1000 kN longitudinal (respectivement transversal) en tête: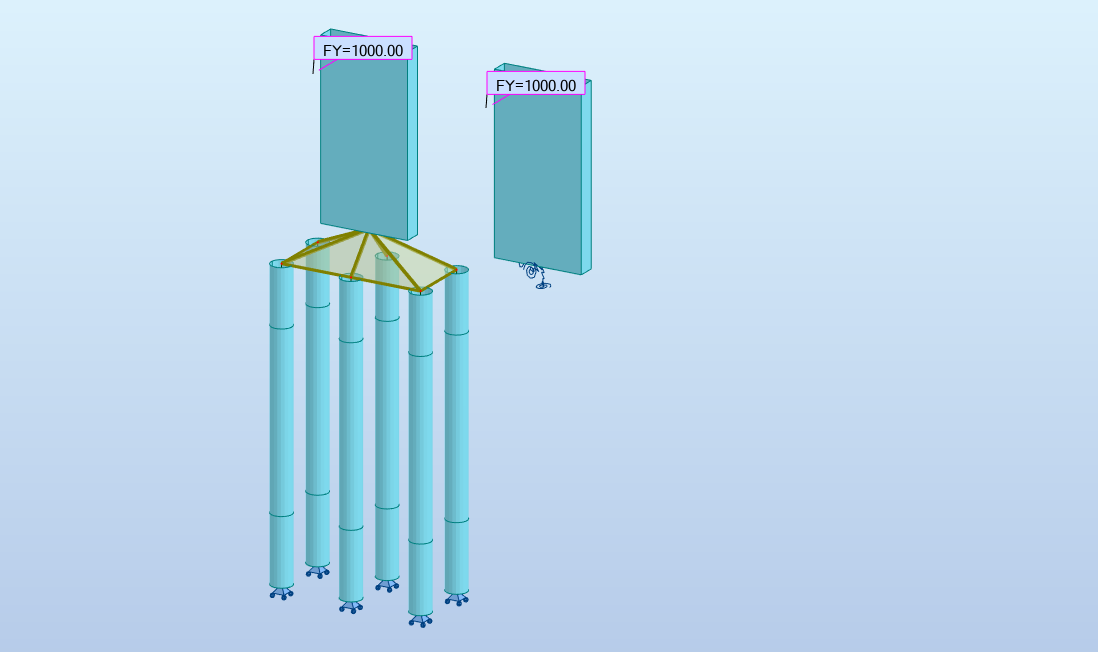

Dans ce cas de figure, on obtient un écart de l'ordre de 13% sur le déplacement longitudinal (respectivement 17% sur le déplacement transversal) - la souplesse de la pile intervient mais elle est identique dans les deux cas. Il appartient à l'ingénieur de juger de l'incidence de cette simplification éventuelle.

Une des sujets qui doit être traité dans la note d'hypothèse générales est relative aux simplifications que l'on va accepter ou non pour le calcul d'ISS. Elle sont liées à la prise en compte, d'une part, des modules à court et long terme du sol (ratio de 2 sur K) et du béton constitutif de la structure (ratio de 3 sur E) et, d'autre part, aux lois de comportements introduites pour le sol (linéaires, à plusieurs pentes, avec un palier de plastification possible). Suivant le logiciel utilisé, vouloir intégrer tous ces facteurs peut s'avérer très complexe, conduire à monter plusieurs modèles différenciés et à effectuer certaines vérifications manuellement (remplacement de ressorts plastifiés par un effort équivalent, par exemple). Effectuer un calcul en fourchette peut s'avérer intéressant dans certains cas, en distinguant les vérifications de résistance de celles de déformations.

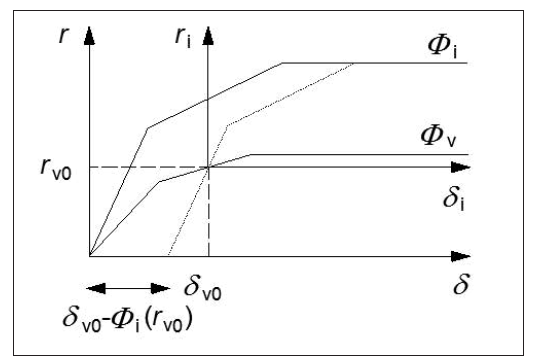
Illustration de la complexité de la loi de comportement des ressorts de sol

C.5.3 Modélisation des appareils d’appui

Les appareils d’appui d’une structure peuvent être modélisés de deux manières :

Dans tous les cas, les appareils d’appui doivent être placés à la position réelle (excentrement transversal et vertical) sous peine de grosses erreurs.

Il est à noter que le comportement des appareils d’appui peut être une source de non-linéarité (appareils d'appui glissants, par exemple) et nécessiter de facto un calcul non-linéaire.

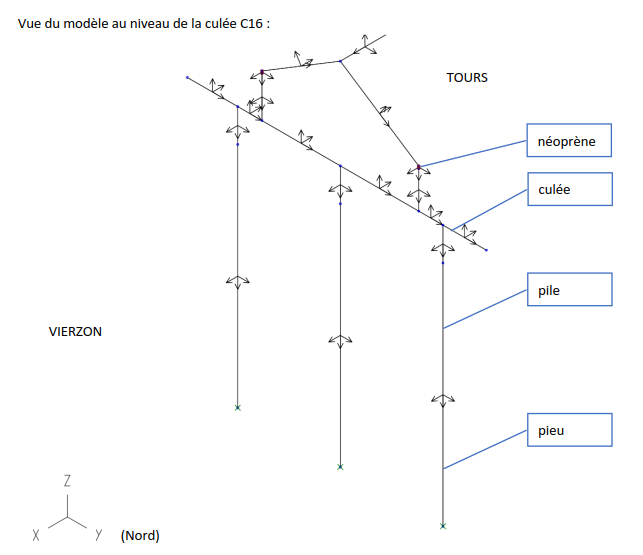
Exemple d’une modélisation d’une pile de pont incluant les appareils d'appui en élastomère fretté.

Si on recourt à des éléments barres, il y a plusieurs choix possibles :

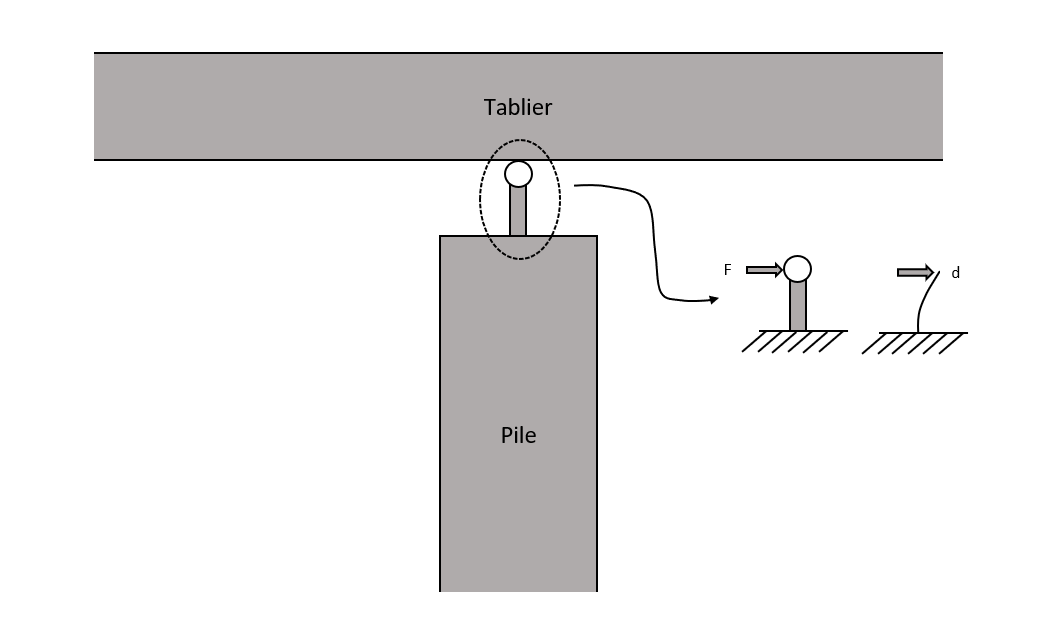
Quelle que soit la méthode, il faut que l’élément ait un comportement global équivalent aux caractéristiques des appareils d’appui, telles que définies par les normes des appareils d'appuis (série NF EN 1337) et il ne doit pas introduire de moment ni dans le tablier, ni dans la pile (autre que celui lié à l'épaisseur de l'appareil). .

L'illustration ci-dessous montre des extension rigides permettant de modéliser une tête de pile supportant deux travées isostatiques, simplement reliées par une dallette.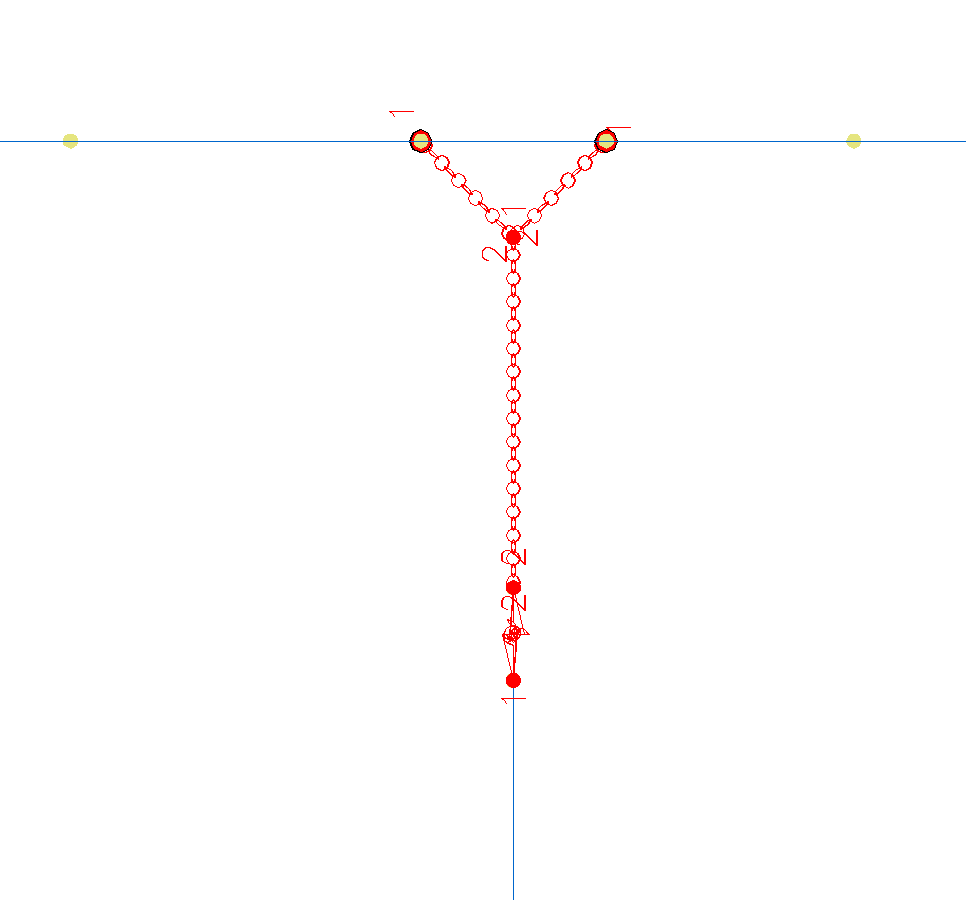
Détail de modélisation d’une pile supportant deux travées isostatiques