C.8 Sections composées (poutres/dalles)
C.8 Sections composées (poutres/dalles)
Les sections composées sont constituées par l’assemblage, rigide ou élastique, d’éléments de nature différente (bois, acier, béton, …) et/ou à des dates différentes.
Nous étudions ici les cas les plus courants rencontrés dans les modélisations :
-
planchers de bâtiments (dalles+poutres) ;
-
poutres d'ouvrages d'art (type PRAD) ;
-
poutres de ponts mixtes acier/béton ;
-
planchers mixtes de bâtiment (profilés métal + dalle BA).
Ces éléments complexifient le calcul avec des approches très différentes selon le cas étudié.
C.8.1 Poutre plancher de bâtiments
Ce chapitre concerne les planchers de bâtiments calculés à partir d'une modélisation globale du bâtiment.
C.8.1.1 Principe du calcul
La difficulté sur ce type d'analyse est de concilier les calculs aux éléments finis avec les règlements de calcul du béton armé.
En effet, les règlements de béton armé (BAEL et EC2-1-1 §5.3.2.1) sont fondés sur des règles précises sur les largeurs participantes, sur le décalage des courbes de moment (qui correspondent à la formation des bielles) et sur le diagramme de déformations des sections (cohérences entre les déformations de la dalle et de la poutre).
Or les modèles éléments finis sont fondés sur la RdM et pas sur ces règlements.
Dans tous les cas, le calcul du ferraillage doit être fait :
-
en tenant compte du sens de portée de la dalle (notamment des éléments préfabriqués) ;
-
en récupérant des efforts du modèle ;
-
en les corrigeant pour tenir compte des largeurs participantes (les bandes non participantes pèsent mais ne portent pas) ;
-
en les corrigeant pour tenir compte des excentrements additionnels non modélisés (verticaux ou horizontaux - effet P-Δ) ;
-
en les corrigeant du décalage des moments ;
-
en refaisant un calcul réglementaire avec ces efforts post-traités.
C.8.1.2 Comment modéliser le plancher poutre/dalle
Le premier point concerne la méthode de modélisation du plancher, en effet plusieurs options se présentent :
-
ne modéliser que les poutres, les charges étant directement appliquées aux poutres ;
-
modéliser les poutres et les dalles sur la même fibre moyenne ;
-
modéliser les poutres excentrées par rapport aux dalles.
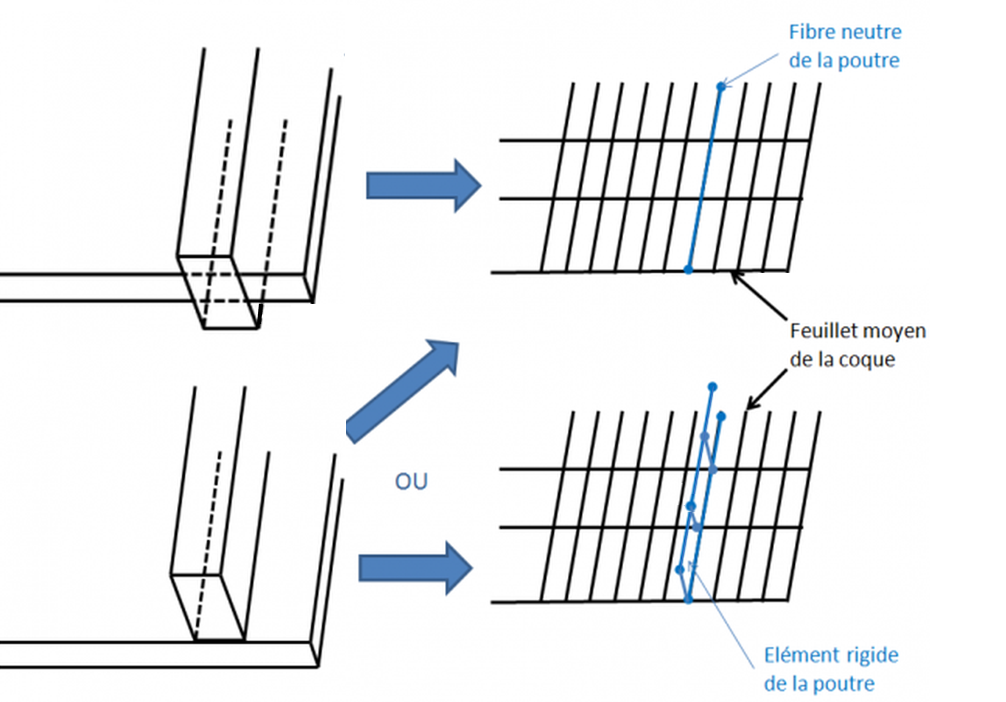
Illustration des deux dernières approches
La comparaison entre ces cas est réalisée à partir de l'exemple suivant :
Soit une structure à 2 travées de 8 m chacune, les poutres 25 cm x 50 cm ht sont espacées de 2 m, la dalle a une épaisseur de 15 cm.
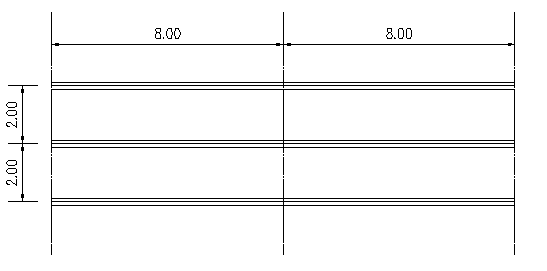
Vue en plan de la dalle
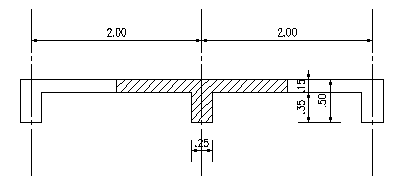
Coupe transversale
On étudiera la poutre centrale :
Chargement = poids propre + charge permanente additionnelle (revêtement) de 3 kN/m2 + surcharges de 5 kN/m2.
Nous étudions le cas ELU (1.35 CP + 1.5 Q).
Il y a 3 types de modélisation :
-
Cas 1 : la dalle n’est pas modélisée, ce qui revient à calculer la poutre selon les méthodes usuelles du béton armé ;
-
Cas 2 : la dalle est modélisée sur la même fibre moyenne que celle de la poutre ;
-
Cas 3 : la dalle est modélisée excentrée par rapport à la poutre.
Etude du cas 1 : modélisation de la poutre seule - la dalle n’est pas modélisée
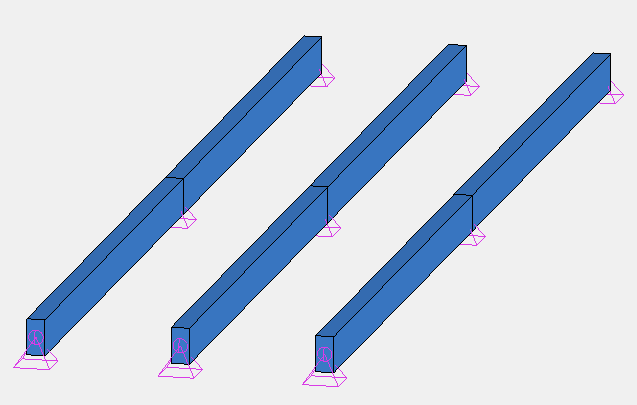
Schéma de la modélisation
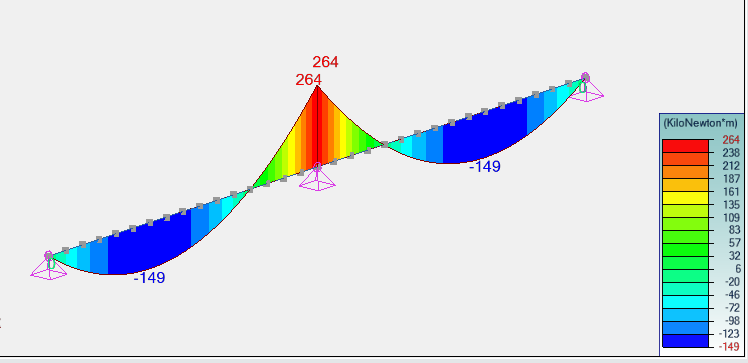
Courbe des moments fléchissants (kN.m) poutre
Les moments fléchissants sont égaux à -264 kN.m sur appuis et 149 kN.m en travée ; ils sont cohérents avec les méthodes classiques de calcul, cela nécessite un ferraillage de 19 cm² sur appuis et de 10 cm² en travée
Etude du cas 2 : la dalle et la poutre sont modélisées sur la même fibre moyenne
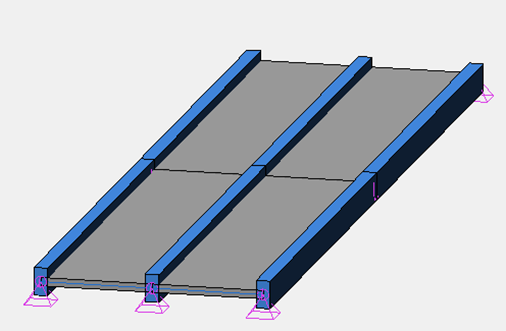
Schéma de la modélisation
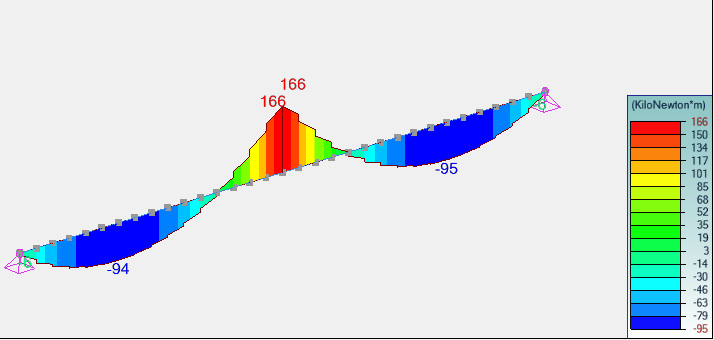
Courbe des moments fléchissants (KN.m) poutre
Les moments fléchissants dans la poutre sont égaux à -166 kN.m sur appuis et 94 kN.m en travée ; ces efforts sont beaucoup plus faibles (-37% !!) que ceux calculés dans le Cas 1 : le ferraillage calculé n’est plus que de 11 cm² sur appuis et 6 cm² en travée.
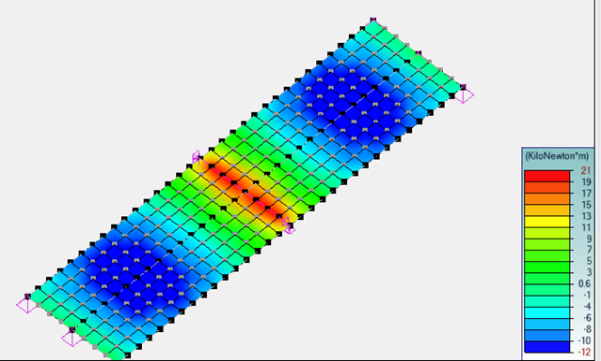
Moments longitudinaux dans la dalle
Les moments fléchissants dans la dalle sont égaux à -21 kN.m/ml sur appuis et 12 kN.m/ml en travée, ce qui se traduit par un ferraillage sur appui As = 5 cm²/ml, Ai = 0 et en travée As = 0, Ai = 3 cm²/ml
Etude du cas 3 : la poutre est excentrée par rapport à la dalle
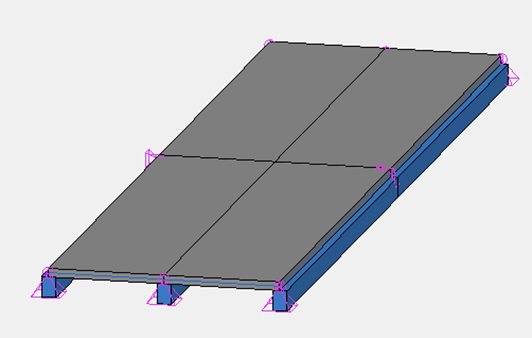
Schéma de la modélisation
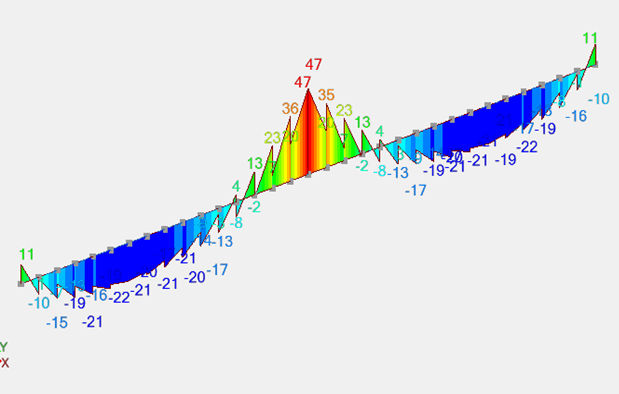
Courbe des moments fléchissants (kN.m) poutre
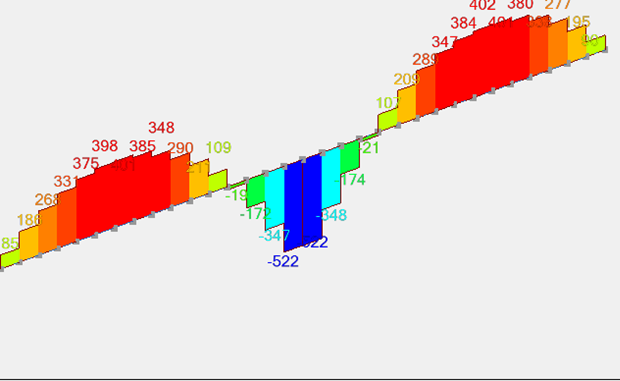
Courbe des efforts normaux (kN) dans la poutre
Les moments fléchissants dans la poutre sont égaux à -47 kN.m sur appuis et 21 kN.m en travée, mais ils sont accompagnés d’efforts normaux (traction sur appuis et compression en travée) ; le ferraillage calculé est alors de 10 cm² en nappe supérieure et 2 cm² en nappe inférieure sur appuis, tandis qu'il n'y a pas d’aciers en travée !!!
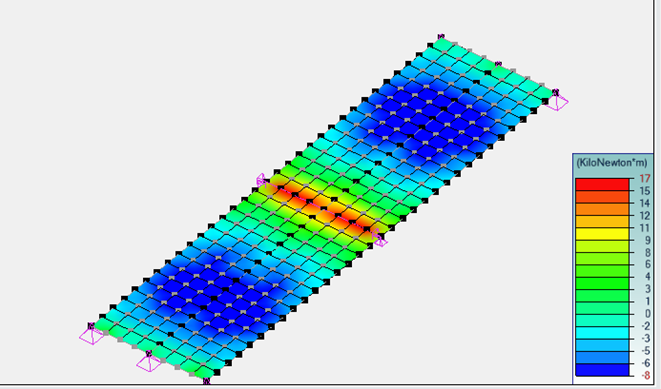
Moments longitudinaux dans la dalle
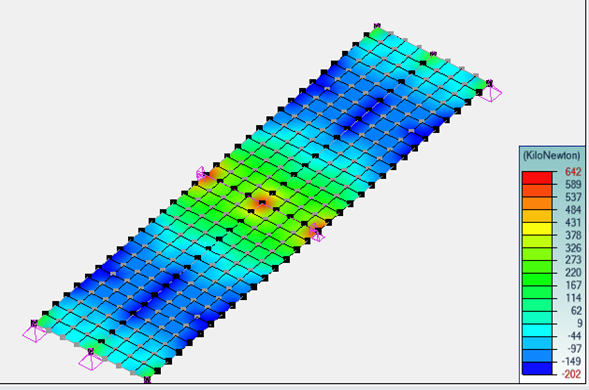
Efforts normaux longitudinaux
Les moments fléchissants dans la dalle sont égaux à -17 kN.m/ml sur appuis et 9 kN.m/ml en travée, ils sont accompagnés d’efforts normaux avec pics sur appuis.
L’analyse montre que le cas 3 avec la prise en compte des excentrements est inexploitable et incompatible avec les calculs réglementaires, car il apparaît des efforts normaux et des pics d’efforts dans la dalle. En effet, comment prendre en compte le décalage des courbes des moments en tenant compte des efforts normaux ?
Les tableaux ci-après résument les principaux résultats.
| Appuis | Travée | ||
| CAS 1 | poutre | 19 cm2 | 10 cm2 |
| dalle | 0 cm2 /ml | 0 cm2 /ml | |
| total | 19 cm2 | 10 cm2 | |
| CAS 2 | poutre | 11 cm2 | 6 cm2 |
| dalle | 5 cm2 /ml | 3 cm2 /ml | |
| total | 20 cm2 | 12 cm2 | |
| CAS 3 | poutre | 10 cm2 | 0 cm2 |
| dalle | inexploitable | inexploitable | |
| total |
Sections d’aciers sur appuis et en travée pour les 3 méthodes de calcul
Les cas 1 et 2 donnent des sections d’aciers proches, ce qui semble valider la modélisation de la poutre et la dalle sur la même fibre moyenne, mais il ne faut pas généraliser les conclusions de cet exemple car, comme le montrent les diagrammes de déformations des sections ci-dessous, il apparait une incohérence en travée avec des aciers tendus dans la dalle, situés au niveau de la zone comprimée de la poutre.
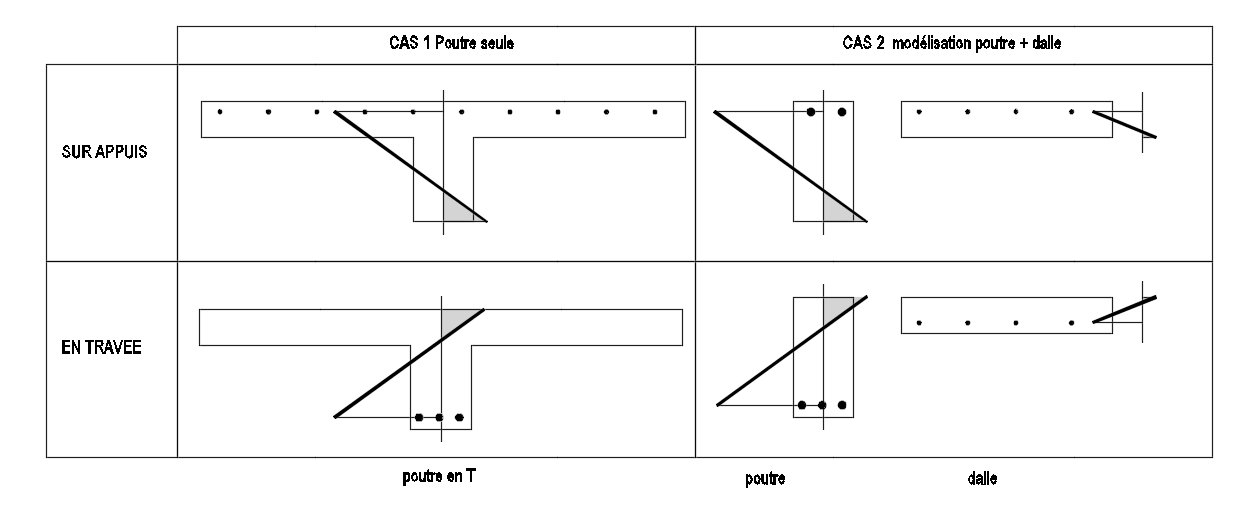
Cet exemple montre que :
-
ne modéliser que les poutres seules donne de bons résultats , mais cette option est difficilement applicable dans une modélisation globale (comment transmettre les efforts horizontaux par exemple ?) ;
-
modéliser un excentrement entre les poutres et les dalles permet une bonne modélisation de la raideur du plancher, mais ce n'est pas compatible avec les vérifications réglementaires (comment décaler la courbe de moments lors qu'une partie des moments apparait sous forme d'efforts normaux dans les poutres ?) ;
-
il ne faut pas calculer les ferraillages des poutres et dalles directement à partir des résultats de la modélisation générale.
C.8.1.3 Méthode générale de calcul d'un plancher poutre/dalle
Les calculs des dalles et des poutres doivent d'une part prendre en compte tous les efforts calculés dans la modélisation globale et d'autre part respecter les règles de calcul réglementaires.
Soit l’exemple d’un bâtiment soumis à des efforts horizontaux (vent, séisme, thermique, etc..) :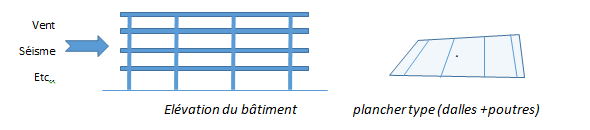
Etape 1 : Réaliser un modèle global du bâtiment. Cette modélisation globale permet de calculer les efforts dans les diaphragmes formés par les planchers, ce qui se traduit par l’apparition d’efforts de membranes (efforts normaux et cisaillements) dans les éléments horizontaux. Ce sont ces efforts que nous retiendrons pour la suite du calcul : Nxx,Nyy,Nxy dans les dalles et Nx dans les poutres.
Etape 2 : Réaliser un modèle local de la dalle. En effet, sauf cas très particulier, il n'est pas possible d'utiliser le modèle global d'un bâtiment pour justifier les dalles car, par exemple :
-
le phasage n'est généralement pas modélisé ;
-
les prédalles ne sont généralement pas modélisées ;
-
le positionnement des charges dans un modèle global ne respecte pas forcément les zones d'influence des poutres et dalles à l'échelle locale ;
-
du point de vue réglementaire, les poinçonnements, les redistributions d'efforts, les majorations forfaitaires des efforts, etc., ne sont pas pris en compte.
Dans le modèle local de la dalle, sa géométrie est extraite de la géométrie du modèle global. Dans un soucis de simplification, les poutres sont généralement remplacées par des appuis linéaires, tandis que les dalles sont modélisées par des éléments de coques (flexion) soumises aux chargements pondéraux. C'est ce modèle plan et de petite taille qui va être étudié de manière réglementaire en tenant compte éventuellement du phasage, des prédalles, etc..
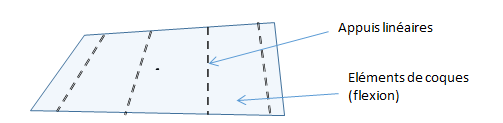
Les efforts de flexion (Mxx,Myy,Mxy) dans les dalles, résultants de ce modèle local doivent être cumulés aux efforts normaux (Nxx,Nyy,Nxy) de la modélisation globale pour calculer les ferraillages et procéder aux vérifications réglementaires (attention aux combinaisons).
Etape 3 : Réaliser un modèle local pour le calcul des poutres. En effet, pour des raisons identiques à celles évoquées pour les dalles, il n'est pas possible d'exploiter le modèle global pour déterminer l'intégralité des sollicitations dans les poutres.
La géométrie est identique à celle du modèle local de la dalle, si ce n’est que les poutres sont bien sûr conservées.
Dans ce modèle, les dalles ne doivent pas reprendre des efforts de flexion, elles doivent simplement jouer le rôle de transmission des charges sur les poutres, elles sont donc modélisées par des surfaces de répartition (se référer à la documentation du logiciel utilisé).
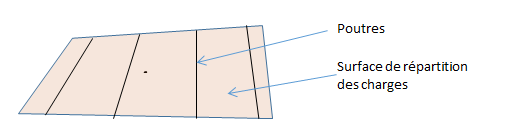
Les efforts résultants dans les poutres sont à cumuler aux efforts normaux de la modélisation générale, ce qui permet de procéder ensuite aux calculs réglementaires des poutres (soit manuellement, soit par logiciel dédié).
C.8.2 Cas des ouvrages d'art (dalles nervurées)
Cette approche s'applique aux ponts de type PRAD, VIPP, …
Pour le calcul des ouvrages d'art, si l'on omet la méthode de Guyon-Massonnet, la pratique consiste à calculer les structures:
-
en grillages de poutres, c'est à dire un croisement de barres longitudinales, représentant la section des nervures + le hourdis participant, et de barres transversales, modélisant le hourdis : l'avantage est que l'on a directement des torseurs exploitables en calcul de béton armé ou précontraint, l'inconvénient peut être le placement des charges, surtout les charges mobiles ;
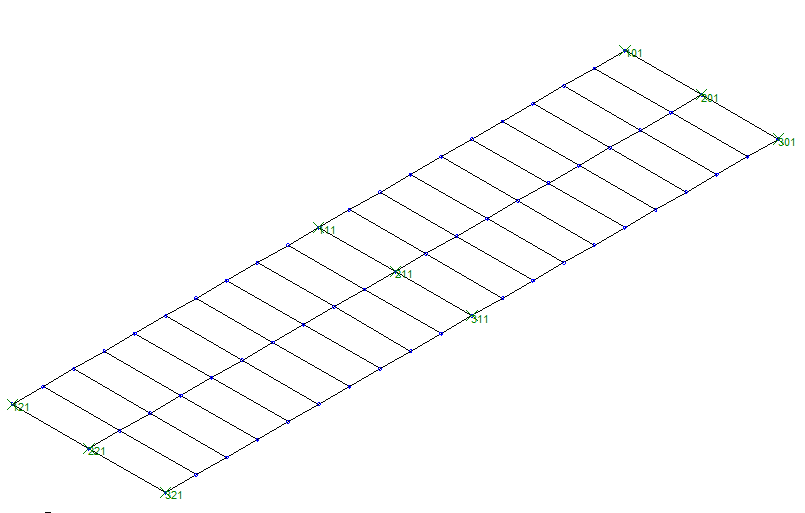
Modèle en grillage de poutres
-
en grillages de poutres utilisant des poutres échelles - peut être avantageux pour un calcul phasé, surtout si l'on veut modéliser finement des effets liés au fluage ou au retrait ;
-
comme dans la troisième approche ci-dessus (C.8.1.2), en modélisant les nervures via des barres et le hourdis excentré sous forme d'une coque EF : l'avantage réside dans le placement facilité des charges, l'inconvénient est que l'on n'obtient pas directement des torseurs exploitables en calcul de béton armé.
Il est à noter que les barres modélisant le hourdis doivent être perpendiculaires (ou quasi-perpendiculaires) entre elles pour que le modèle soit valide.
Pour illustrer cette approche, en particulier le ferraillage du hourdis et des nervures, nous repartons de l'exemple traité en C.8.1.
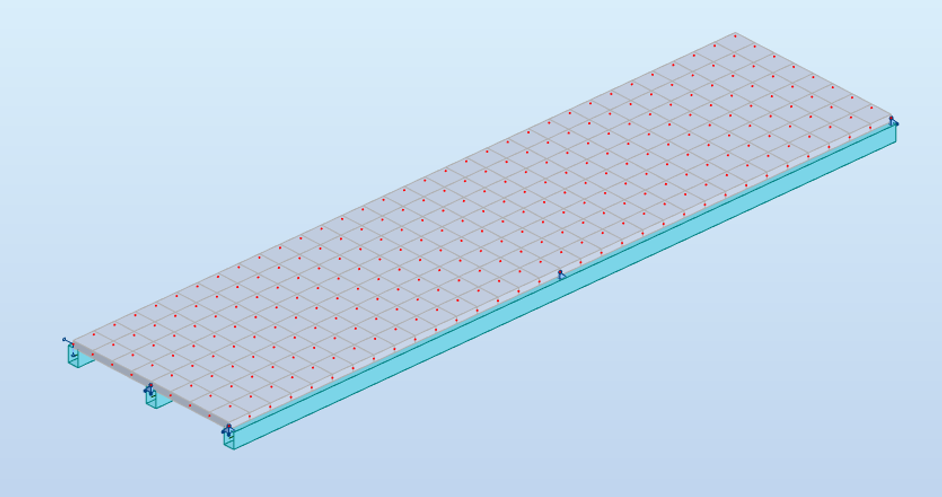
Vue du modèle – retombées 25 cm x 35 cm ht et hourdis de 15 cm d’épaisseur. Portées 2 x 8 m – entraxe des poutres 2 m.
Le calcul des armatures directement à partir d’un module de ferraillage n’est pas recommandé si l’on veut tenir compte des hypothèses en usage pour le calcul du béton armé. Un petit post processeur (un tableur) suffit à calculer le moment et la largeur de table affectée à la nervure, comme nous le verrons ci-après.
Application à la poutre centrale du modèle - section sur appui et section en travée (nota: les deux travées sont chargées par la charge d'exploitation en totalité, sans considération de ligne d'influence):
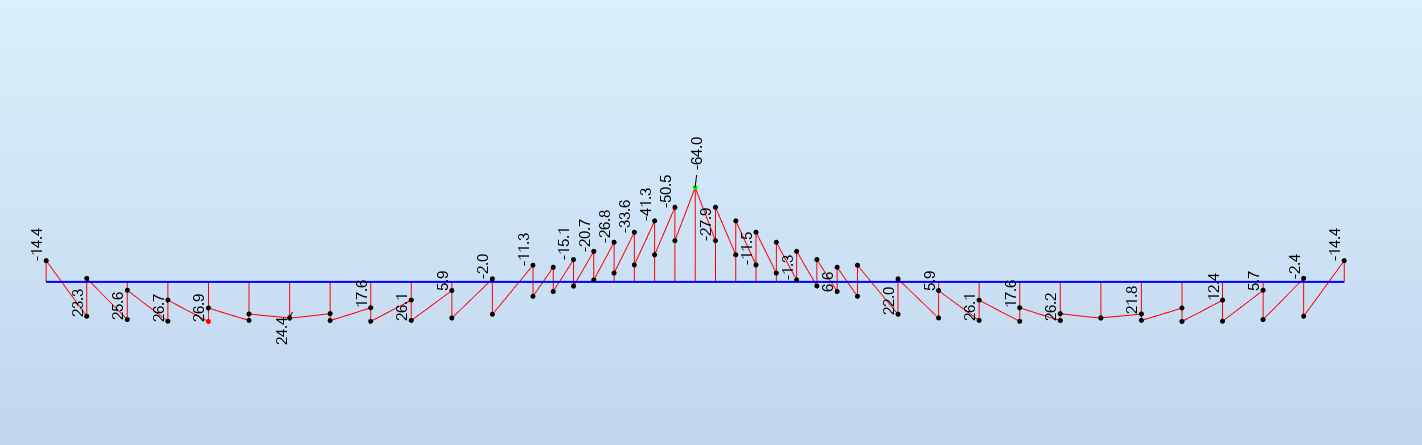
Moments de flexion (retombée seule) - kN.m
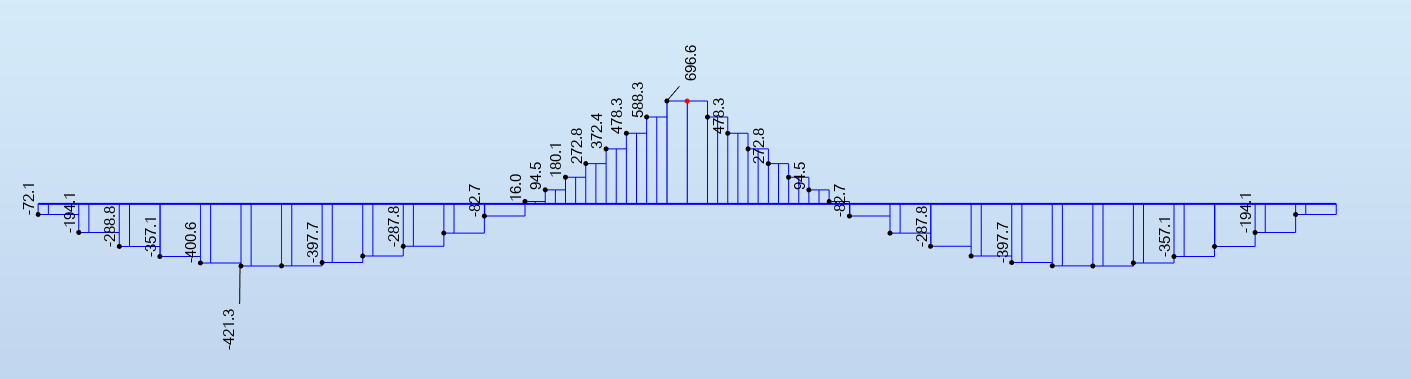
Effort normal (retombée seule) - kN
La méthodologie consiste à appliquer le principe courant de la conservation des sections planes et à calculer l'équilibre (élastique) des efforts internes. 1. Le diagramme des contraintes est prolongé pour obtenir la contrainte sur la fibre supérieure (dessus de dalle) 2. L’effort normal sur la section composée est nul : l’intégration des contraintes normales doit donner une résultante nulle, la largeur participante de hourdis s’en déduit 3. Tous les paramètres géométriques et de contraintes sont déterminés, il ne reste alors plus qu’à calculer le moment résultant du diagramme des contraintes.
Application au cas de la section sur appui :
On note une largeur de table réduite (47 cm), ce qui est logique compte tenu de l’effet de traînage de cisaillement. As=14.4 cm² (calcul aux ELU).
Application au cas de la section en travée :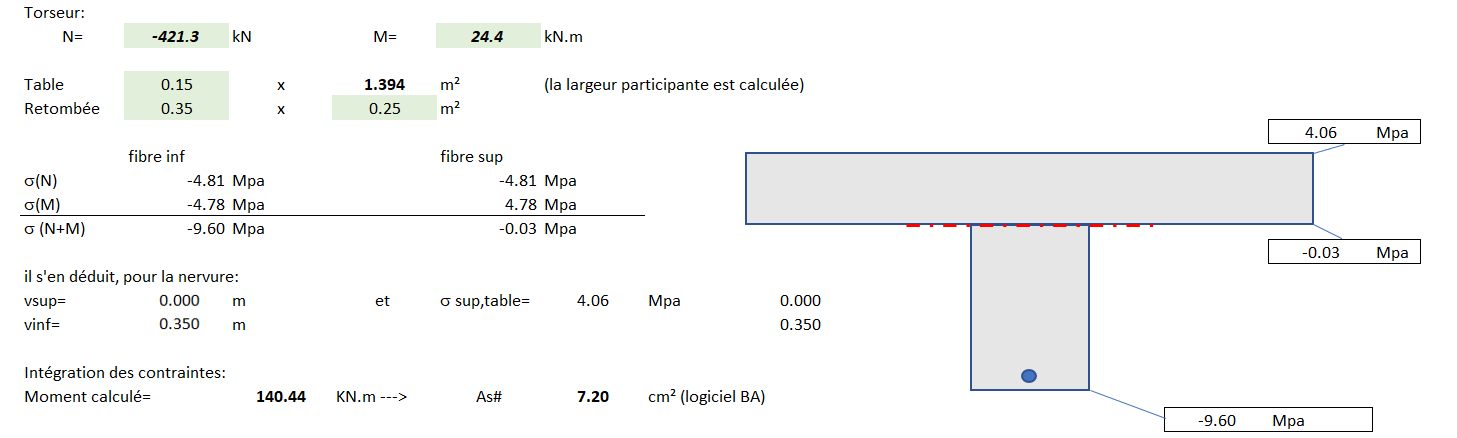
On note une largeur de table plus conséquente (139 cm), valeur logiquement plus importante que sur appui. As=7.20 cm² (calcul aux ELU).
Si on effectue un calcul automatisé dans la nervure et dans la dalle :
→ Le logiciel propose des sections d’armatures à des localisations qui, de fait, n’en nécessitent pas lorsque l’on effectue un calcul de béton armé «manuel» (il a bien été vérifié en parallèle qu’aucune section d'acier comprimée n’était nécessaire).
→ Dans le cas présent, l’approche automatisée conduit à un très léger déficit d’armature inférieure en travée et un surplus d'armature en fibre supérieure.
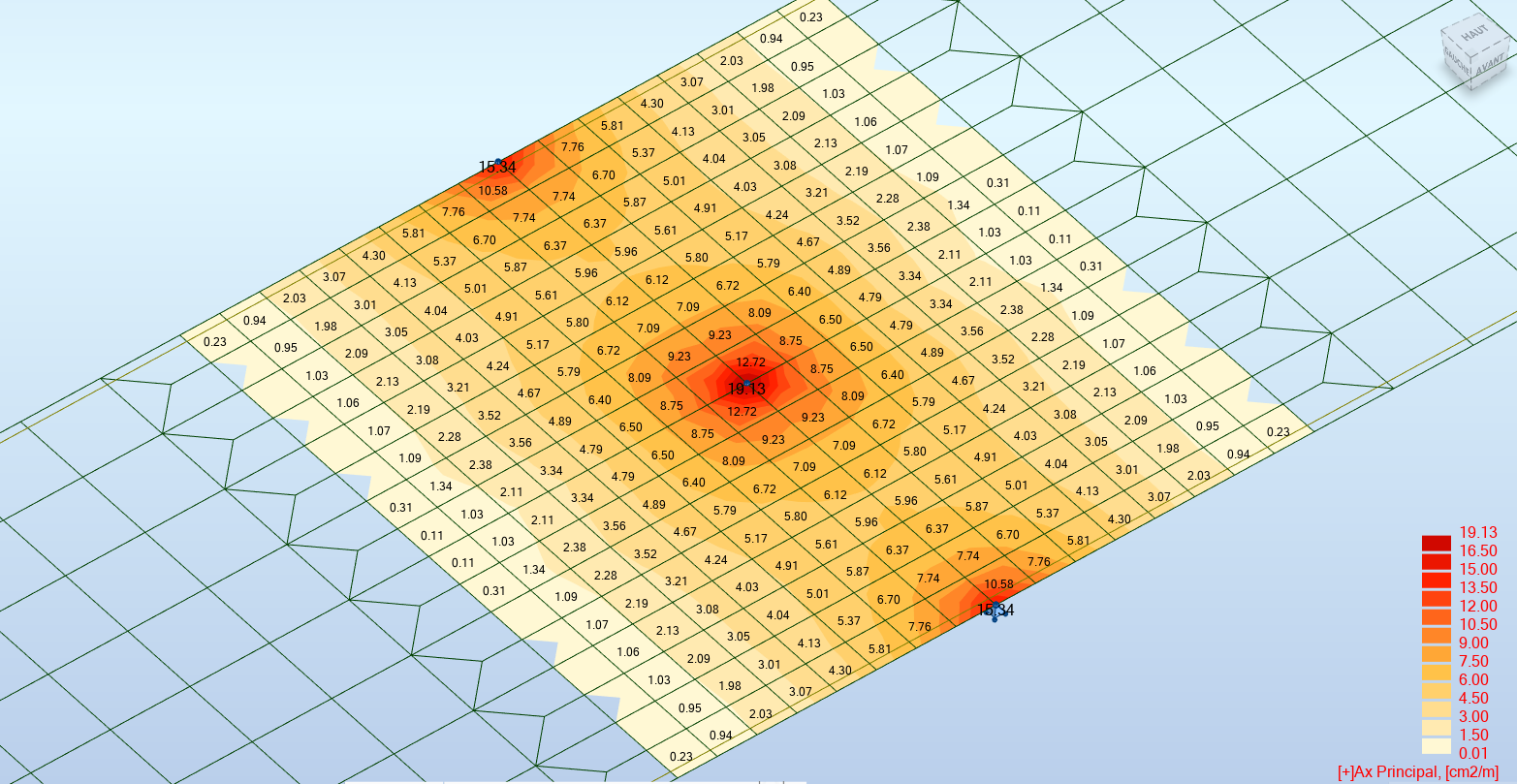
Cartographie des armatures en fibre supérieure du hourdis
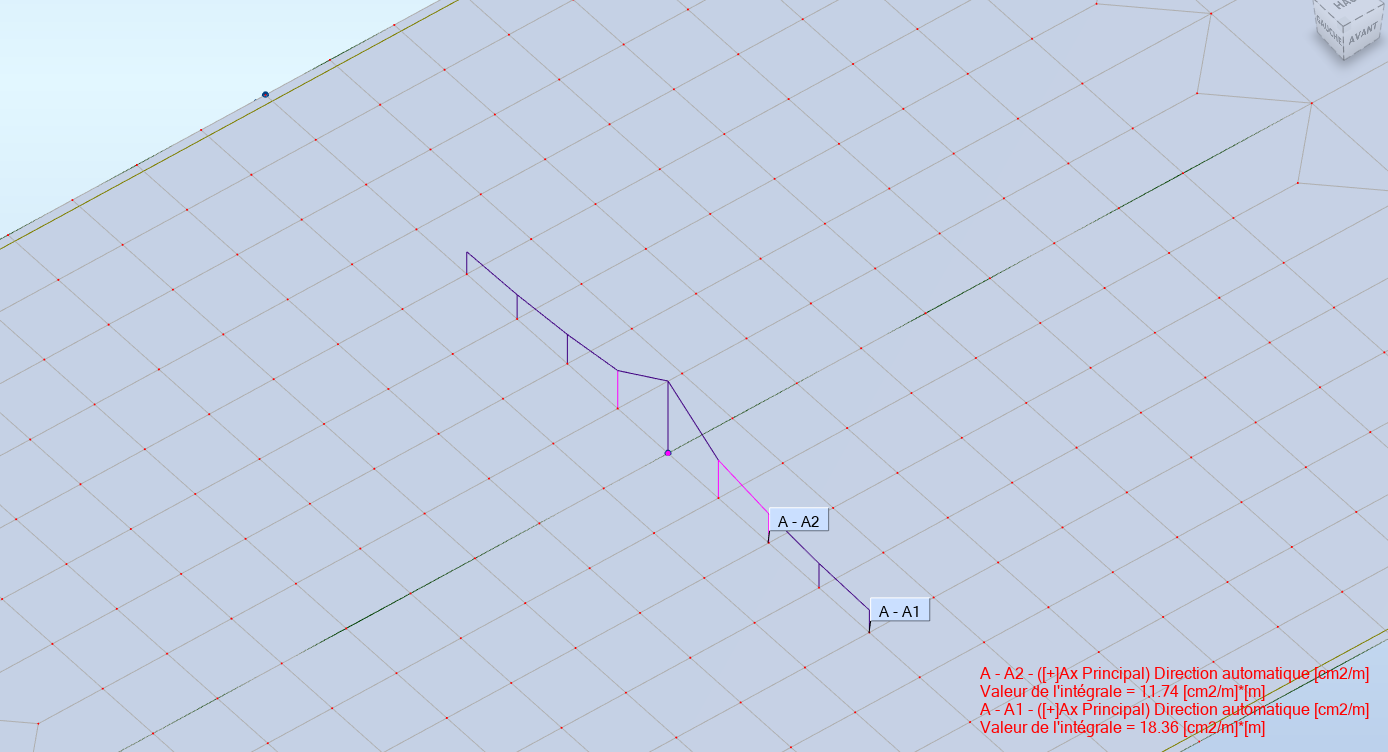
Armatures en fibre supérieure du hourdis sur l'appui central, poutre centrale (18.36 cm² sur 2 m)

Armatures en fibre inférieure du hourdis
Les efforts calculés via le modèle en grillage de poutres sont les suivants et conduiraient à 7.2 cm² en travée et 15.4 cm² sur appui: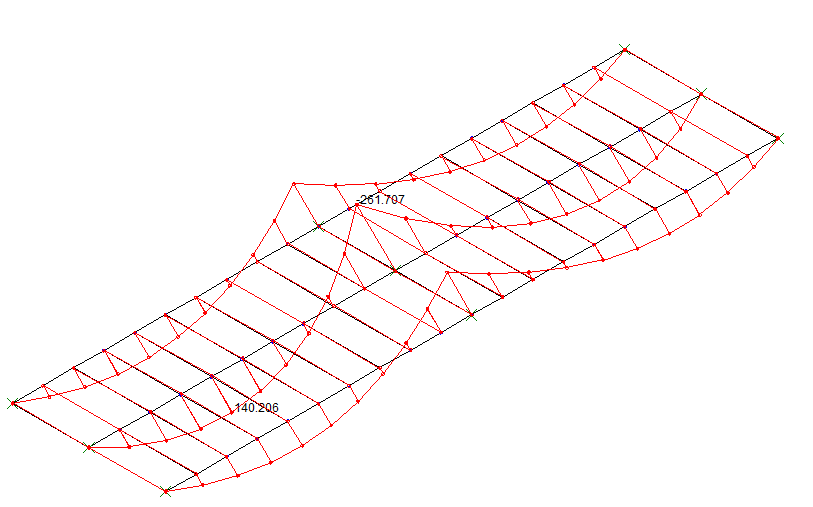
Modèle grillage de poutres (Mt = 140 kN.m, Ma = -262 kN.m) - sans prise en compte des largeurs participantes
En conclusion, sur l'exemple ci-dessus, on se rend compte que le calcul automatisé du ferraillage n'est pas satisfaisant. Sans considération de % mini, il conduit à placer des armatures dans des zones où un calcul réglementaire n'en demanderait pas et à sous et sur-armer certaines zones. En sus, rappelons encore un fois que le calcul automatisé ne tient compte ni d'un décalage de la courbes des moments, ni du poinçonnement, ni des bielles d'about… Il appartient, encore une fois, à l'ingénieur d'analyser les résultats et de tenir compte ou non de certains d'entre eux. Notons que la problématique de lissage des efforts ou des armatures se pose à nouveau en cas d'utilisation d'EF de type dalle ou coque.
D'autres exemples sont donnés en Exemple C - Modélisation de grillages de poutres.
C.8.3 Poutres et dalles mixtes acier-béton
En règle générale, on modélise le caractère composé des sections. Dans certains cas, toutefois, la modélisation peut se limiter à la poutre principale seule, sans tenir compte du phasage, par exemple, pour un prédimensionnement. Après calculs, les sollicitations de la poutre métallique sont alors utilisées pour venir dimensionner et vérifier le comportement de la poutre mixte selon le référentiel réglementaire approprié. Le modèle ne détecte pas que c'est une poutre mixte et il y a une petite erreur sur la raideur dont il faut évaluer l'acceptabilité.
Lors de la justification réglementaire de la poutre, il conviendra de tenir compte du caractère mixte et du phasage de construction.
Approches de modélisation :
Pour un calcul plus rigoureux, il est possible de modéliser la poutre mixte :
-
soit sous forme d’une poutre dont les caractéristiques mécaniques tiennent compte de la connexion de l'acier et du béton. Pour cela, on appréhende la différence des modules d'Young des deux matériaux via un coefficient d'équivalence - on dit dans cas qu'on homogénéise les matériaux, généralement en ramenant le béton à une équivalence métal. (a)
-
soit par deux poutres superposées, l'une, inférieure, métallique, l'autre, supérieure, en béton, à l'altimétrie de leur centre de gravité respectif. Ces barres sont reliées à leurs extrémités par des liaisons rigides. Ceci peut faciliter la prise en compte d’un retrait et d’un fluage différentiel. Si l'ouvrage est modélisé dans sa globalité, les barres longitudinales en béton décrites ci-dessus sont, en complément, reliées par des barres transversales de manière à former un “grillage” de poutre. (b)
-
on peut également choisir de remplacer les éléments de barres du hourdis par des éléments finis de type coques ( c). Dans ce cas, le calcul des torseurs nécessite un post-traitement, idéalement automatisé, suivant la méthode décrite en C.8.2.
Les approches (b) et ( c) sont à réserver à des cas particuliers, car, si dans un premier temps elles peuvent paraître plus simples, les pré- et post-traitements sont toujours beaucoup plus longs qu'avec un modèle de type (a), surtout si l'on utilise un logiciel dédié aux calculs mixtes.
Pour tenir compte du phasage, on doit, à chaque modification d'état, soit modifier l’inertie de la poutre homogénéisée (a), soit activer les poutres du hourdis (b) ou les coques ( c), par exemple dès lors que le béton a fait prise et est décoffré. Il faut bien sûr tenir compte du fluage du béton, soit à l'aide d'un coefficient d'équivalence, soit via une loi de fluage et des zones dites fissurées.
Exemple d'un ouvrage mixte modélisé suivant l'approche (a) :
Exemple d'un ouvrage mixte dont la dalle est modélisée par des éléments de coque excentrés - approche ( c). Les poutres métalliques sont dans ce cas modélisées strictement suivant la répartition matière (métal seul):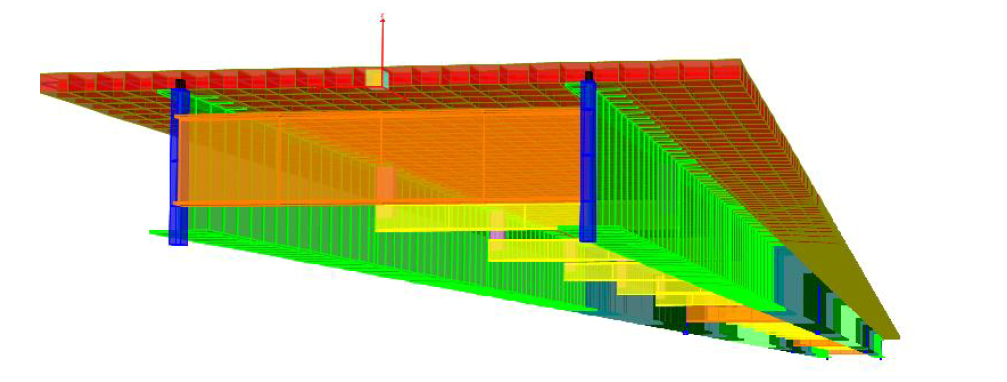
L'emploi d'un logiciel spécifiquement développé pour les calculs mixtes est toujours recommandé lorsque cela est possible.
Voir en Partie 3, l'exemple B - Bipoutres mixtes et métalliques.
C.8.4 Plancher mixte (bâtiment)
Un plancher mixte est composé de poutres métalliques supportant des dalles en béton armé (prédalles ou non) ou en bac acier métallique.
C.8.4.1 Charges pondérales et verticales : sens de portée des dalles
Les calculs des efforts dans un plancher mixte sont réalisés en considérant la résistance des poutres métalliques seules. Le béton est alors considéré comme un poids mort non résistant. De plus généralement ces planchers sont constitués de bacs aciers collaborants qui ne portent que dans un seul sens. Ces particularités nécessitent des dispositions spécifiques dans les modélisations.
Dans le cas de géométrie simple, la dalle en béton n’est pas modélisée et les charges sont appliquées directement sur les profilés métalliques.
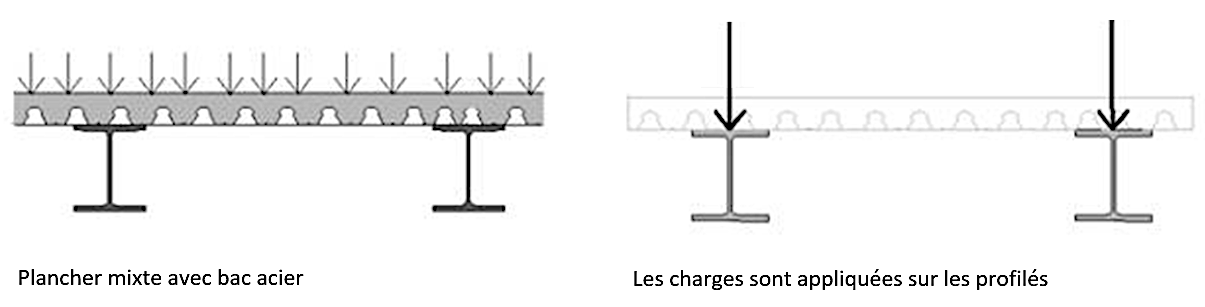
Lorsque la géométrie est complexe, la répartition manuelle des charges sur les profilés devient trop délicate, il faut alors faire appel aux calculs des répartitions des charges par le logiciel en utilisant les surfaces de répartition. Les logiciels les plus courants possèdent ce type d’élément qui se comporte comme une plaque d’épaisseur très faible, sans rôle résistant mais répartissant les charges sur les poutres porteuses. Des options permettent de prendre en compte les sens de répartition des bacs aciers, mais cela demande une grande attention afin de bien respecter les sens porteurs, les vérifications sont indispensables. Prenons l’exemple des pétales de la fondation LUMA à Arles constituées de plancher mixte avec bac acier, elles sont représentées en bleu dans le schéma ci-après …
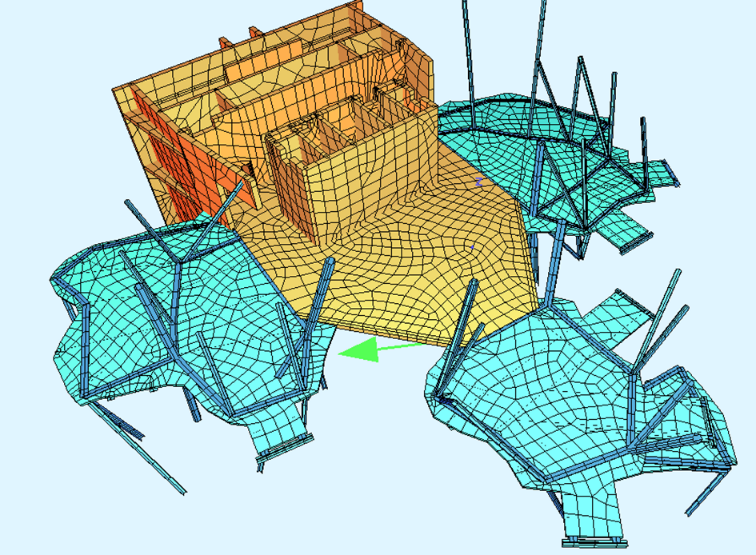
Les surfaces de répartition en bleu sont maillées comme des dalles, mais ne participent pas à la résistance de la structure.
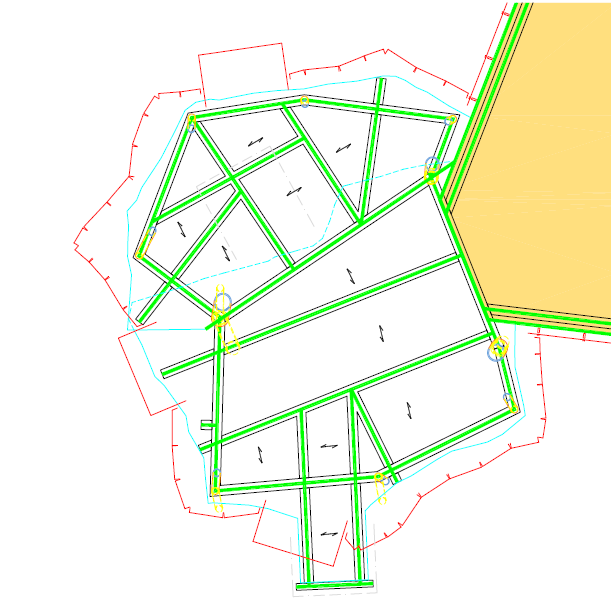
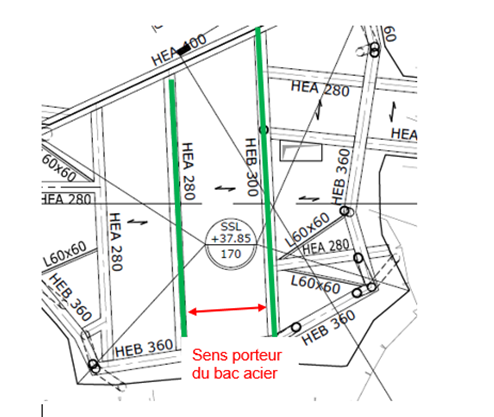
Vue en plan du plancher avec le sens porteurs des bacs acier

Visualisation des chargements des poutres calculés directement par le logiciel
Les calculs sont ensuite menés classiquement.
Le calcul des dalles en tant que tel se fait alors par un calcul spécifique de dalle (orthotrope) entre poutres.
C.8.4.2 Charges horizontales (vent, séisme)
Dans les cas usuels, la dalle en béton est désolidarisée des porteurs afin de ne pas participer au contreventement du plancher. Ce dernier est alors assuré par des contreventements horizontaux métalliques.
Mais dans certains cas complexes, il peut être nécessaire de contreventer les planchers en utilisant la dalle en béton. La modélisation devient alors très complexe :
-
la dalle doit être modélisée avec une excentricité par rapport à la fibre moyenne des profilés ;
-
il est nécessaire de modéliser les connecteurs entre la dalle et les profilés ;
-
le nœud de jonction dalle/poteau est différent du nœud de jonction profilés/poteau.
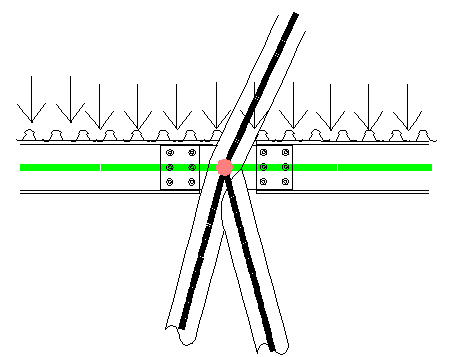
Plancher mixte sans modélisation de la dalle - Contreventement assuré par les profilés
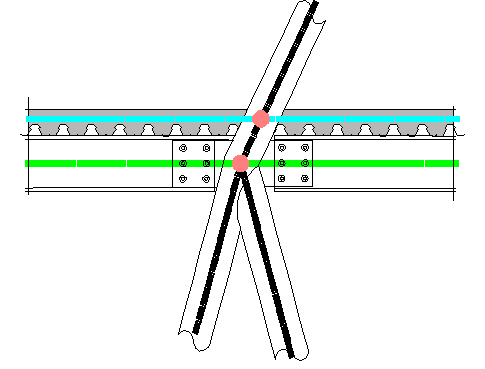
Contreventement assuré par la dalle
Pas de commentaires