C.2 Modélisation des éléments principaux

C.2 Modélisation des éléments principaux

C.2.1 Construction de la géométrie

La première étape de modélisation consiste à construire la géométrie du modèle par la définition des points, lignes, contours, aires et volumes. Les notions de nœuds, d’éléments et de mailles sont associées, quant à elles, aux éléments finis.

Dans certains logiciels, on peut faire une construction géométrique avant de créer les nœuds, éléments et mailles. Dans d’autres, on établit la construction géométrique en dehors du logiciel, au moyen de schémas ou de tableurs Excel, et on définit ensuite directement les nœuds, éléments et mailles dans le logiciel.

Dans tous les cas, les conventions de signes utilisées par le logiciel doivent être connues dès le démarrage de la modélisation (direction de la pesanteur dans le repère général, convention sur le signe des moments, efforts et contraintes).

Quelques notions générales :

C.2.2 Degré de simplification : trémies et évidements

Suivant la phase d’étude et le type de calcul mené (par exemple une stabilité ou une descente de charge), on ne modélisera pas forcément toutes les ouvertures.

Cas du bâtiment.

Pour les bâtiments, dès lors qu'elles sont prises en compte, il est conseillé, autant que possible, d’intégrer à la géométrie les trémies de taille non négligeable et pouvant remettre en cause le comportement de la structure (a minima dans les éléments de contreventement). Cette dernière sera découpée en fonction des intersections voiles/voiles, voiles/planchers, trémies, de façon à avoir un maillage le plus régulier possible.

Dans le cas de la modélisation d’un bâtiment, la définition des trémies est effectuée en fonction :

Une attention particulière doit être portée sur les linteaux des portes des voiles porteurs (et de contreventement), en effet ces linteaux sont généralement percés par de nombreuses réservations, ils peuvent alors ne plus être capables d'assurer leur rôle structurel, ce qui nécessite une modélisation adaptée.

Lorsque les réservations ne sont pas connues, les modélisations des bâtiments soumis à des efforts horizontaux (vent, séisme) doivent prendre en considération des mesures conservatoires concernant les grosses trémies (de ventilation généralement). Il est souvent nécessaire de réduire fictivement l'épaisseur des linteaux, voire de les supprimer des modélisations.

Exemple de regroupement d'ouvertures :

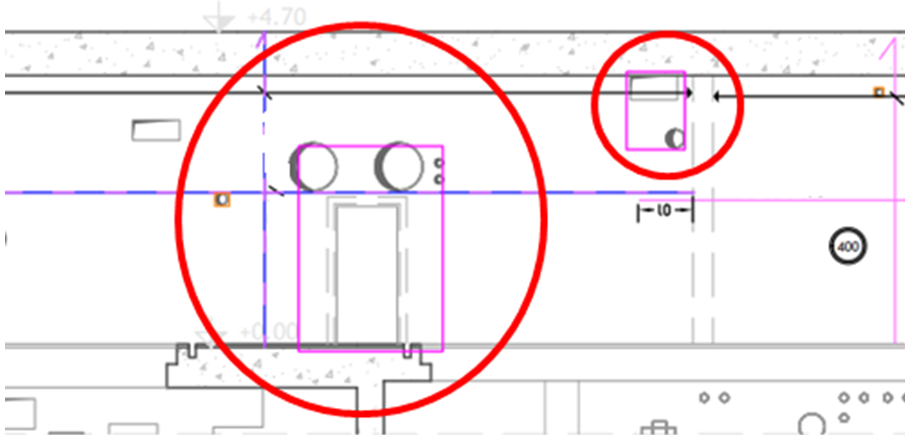
Exemple de structure avec des trémies conséquentes… qui ne peuvent clairement pas être négligées.

Cas de la construction métallique. Les recommandations de la CNC2M pour le dimensionnement des poutres en acier avec ouvertures dans l’âme selon la NF EN 1993 précise qu’une ouverture isolée présentant une dimension maximale inférieure à 10% de la hauteur de l'âme de la poutre n'est pas considérée comme significative. D’un point de vue modélisation de ces ouvertures, la même règle peut être appliquée. Néanmoins, cette ouverture doit être prise en compte lors de la vérification de la section selon les règles habituelles de la NF EN 1993.

Dans le cas d’un dimensionnement avec collaboration de paroi, avec des diaphragmes constitués de plaques nervurées, conformément à l’EN 1993-1-3 § 10.3.4, des ouvertures de petites dimensions, régulièrement réparties, dont la surface cumulée représente jusqu’à 3% de la surface totale peuvent être disposées sans calcul particulier du diaphragme sous réserve que le nombre total de fixations des panneaux constituants le diaphragme soit respecté. D’un point de vue modélisation, de telles ouvertures peuvent donc ne pas être prises en compte.

C.2.3 Degré de simplification : courbure, dévers, …

Au stade de la modélisation de la géométrie, à l'échelle d'un élément structurel, les éléments courbes devront être représentés de façon aussi précise que possible, sachant que l’étape du maillage discrétisera ces courbures par une succession de segments droits, en fonction de la taille de maille choisie et des nœuds déjà définis. La partie des Eurocodes NF EN 1993-1-6 traitant de la résistance et de la stabilité des structures en coque donne quelques indications sur la prise en compte de la courbure.

Pour les ouvrages d’art il convient de s’interroger sur les effets du dévers, de la courbure et du biais et leur non-prise en compte doit être dûment justifiée. Pour les ouvrages rectilignes courants, le dévers étant normalement limité lors de la conception, il est généralement possible de le négliger. En revanche pour les ouvrages d’art courbes :

Pour fixer un ordre de grandeur, on peut considérer qu'un ouvrage est peu sensible:

Il est cependant difficile d'édicter des règles générales et le lecteur est invité à consulter les guides de conception propres à chaque typologie d'ouvrage (PRAD, PIPO, PICF, …).

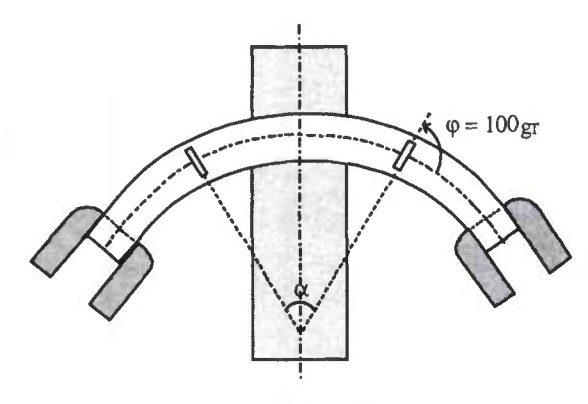
Illustration de l'ouverture angulaire entre deux appuis

L'exemple de grillage de poutres "Modélisation d'un même ouvrage suivant différentes approches" (en Partie 3) illustre les effets du biais et du dévers sur un exemple de ponts à poutres.

C.2.4 Degré de simplification : alignement des voiles d’épaisseur variable

Dans le cas d’un bâtiment, les règles de l'art préconisent un alignement des éléments verticaux de façon à assurer une descente de charges simple. Toutefois, des exigences diverses (équipements abrités, espace disponible…) peuvent amener à certains décalages d’un niveau à l’autre. Une simplification de la géométrie lors de la modélisation peut cependant être faite (notamment afin d’éviter un maillage trop hétérogène) par alignement des éléments verticaux et même des éléments horizontaux.

Cette simplification aboutit à une bonne représentation du fonctionnement global de la structure, sous réserve du respect des dispositions constructives recommandées. Il faut toutefois faire une vérification locale du bon fonctionnement du transfert des efforts et réintégrer les excentrements réels dans cette vérification locale.

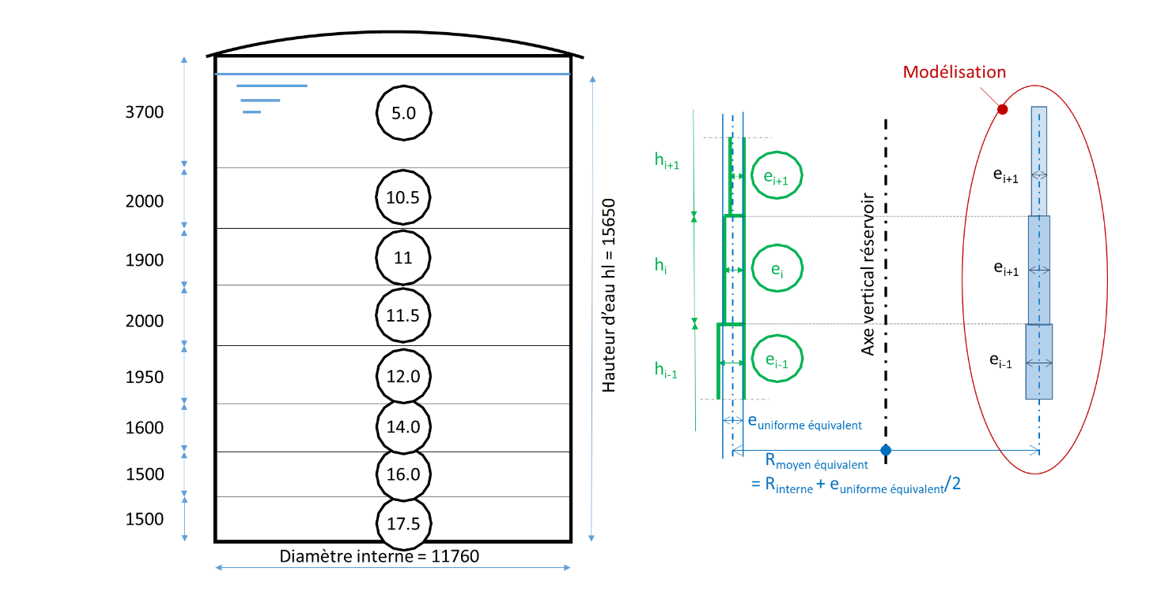
De même, pour les structures métalliques, en présence de semelles ou de tubes d’épaisseur variable (viroles par exemple), il est d’usage d’utiliser un plan moyen unique.

Par exemple, un réservoir composé de viroles ayant des hauteurs et des épaisseurs différentes sera modélisé par des surfaces cylindriques présentant :

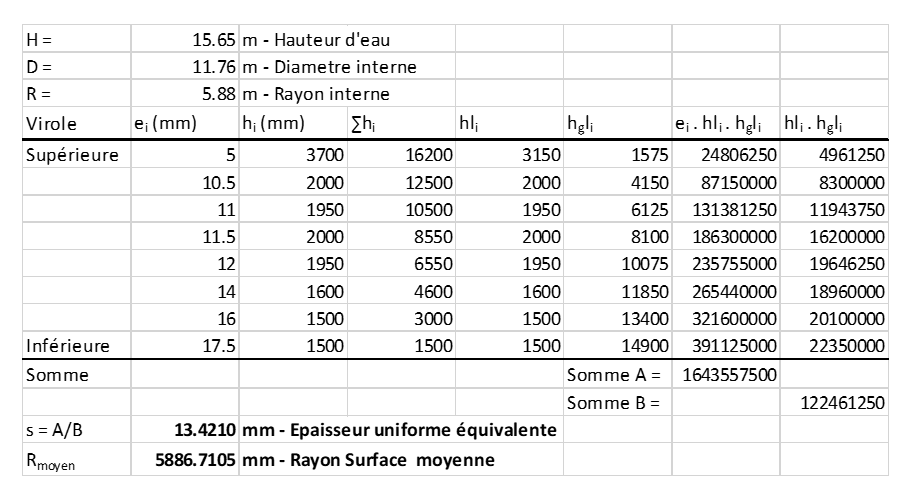
La valeur du rayon moyen équivalent peut être définie d’après le Guide Séisme Réservoirs de stockage DT108 qui donne des exemples de détermination d’une épaisseur uniforme équivalente, ce qui permet de définir la valeur du rayon moyen équivalent = Rayon interne de la virole + Demi-épaisseur uniforme équivalente (voir exemple ci-après) :

C.2.5 Utilisation de la symétrie

Comme évoqué dans la Partie 1 A2. Dimensionnalité de la modélisation, dans le cas où la structure présente, dans sa géométrie, un plan ou des plans de symétrie, il peut être très intéressant, pour limiter les temps de calcul et la taille des modèles, d’utiliser cette symétrie, en ne modélisant qu’une partie de la structure et en définissant des conditions appropriées aux limites sur le plan de symétrie.

On prêtera cependant une attention au fait que le chargement doit aussi être symétrique et que la solution obtenue sera symétrique (par exemple, les modes propres antisymétriques n’apparaîtront pas).

Exemple 1 : Pont à 4 travées, symétrique

Les travées font 60/100/100/60 m. Le pont est symétrique par rapport à son point médian.

On pourrait être tenté de modéliser la moitié du pont, en plaçant une condition d’appui de symétrie en ce point (à droite sur la figure, translation verticale bloquée, rotation bloquée) :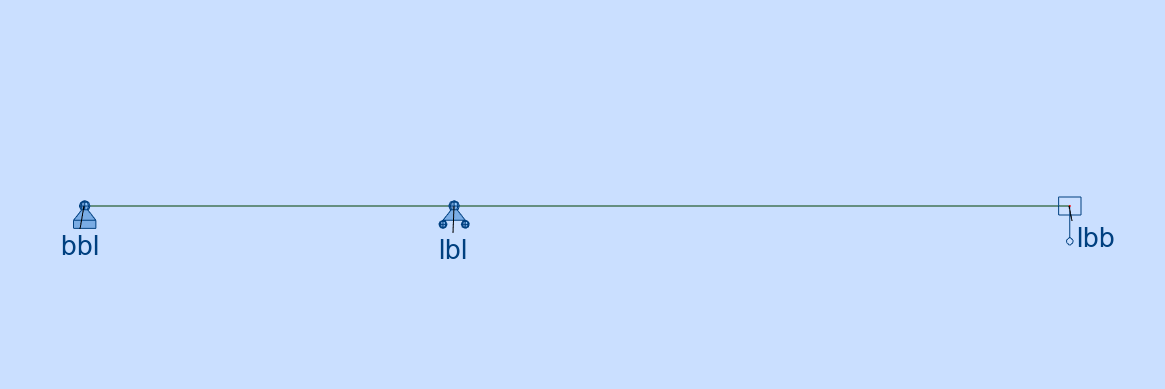

Cas de charge symétrique :

Dans ce cas, les résultats sont identiques pour les deux structures.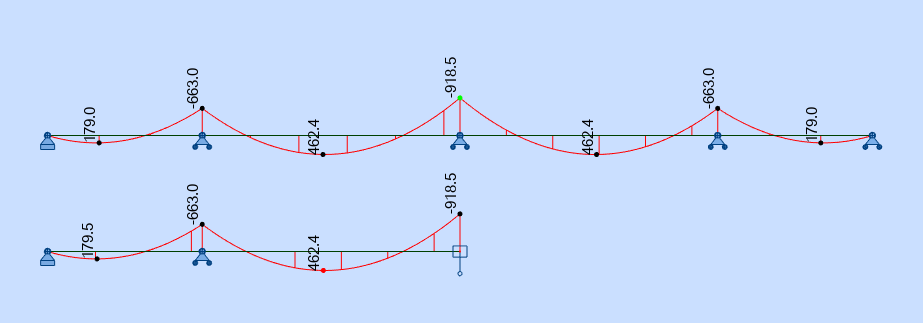

Cas de charge dissymétrique :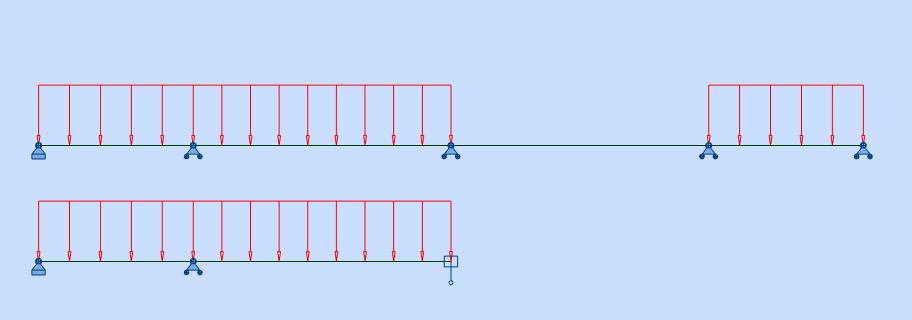

Dans ce cas, on note un écart notable dans les résultats :

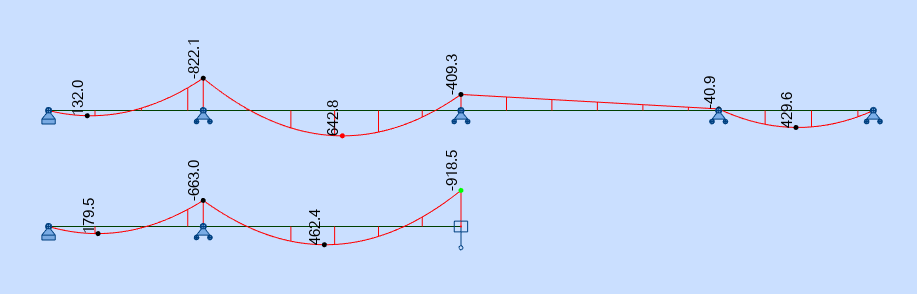
L'examen des lignes d’influence du moment sur le second appui dans les deux configurations fournit une explication immédiate :

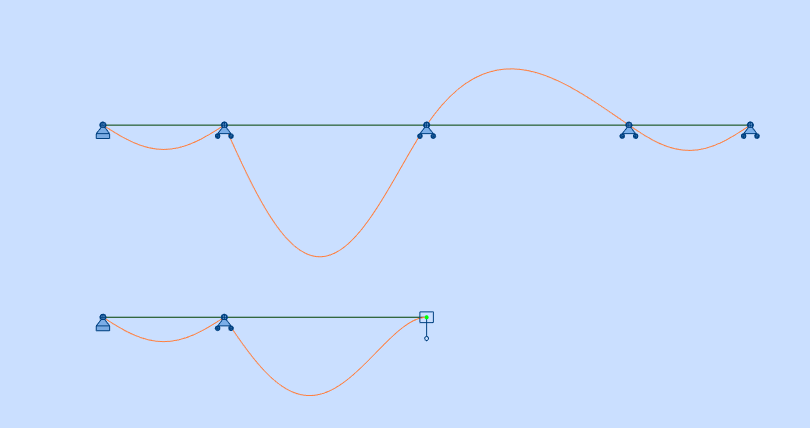
Exemple 2 : Radier

Radier de forme carrée, modélisé par des éléments coque.

Les nœuds possèdent 6 degrés de liberté (ux, uy, uz, rx, ry, rz).

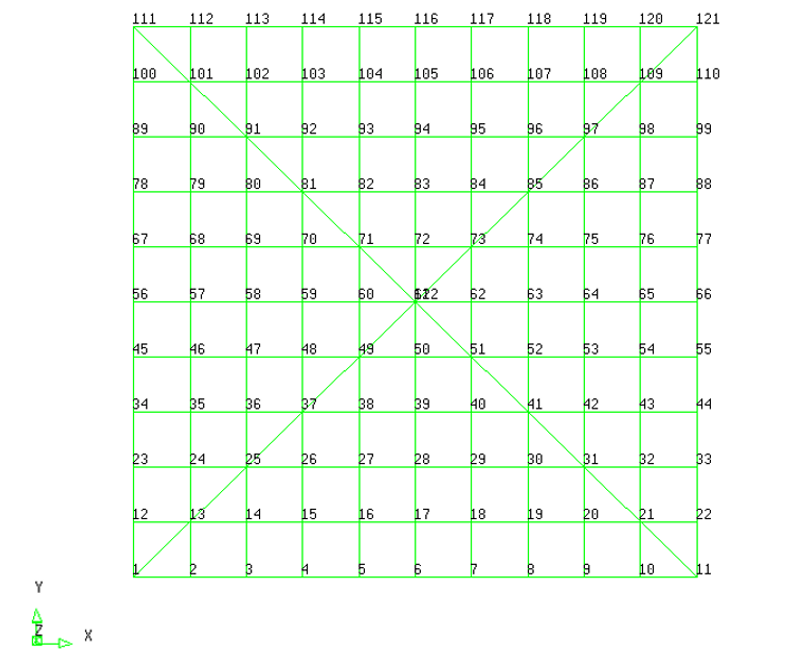
Par sa forme, il présente des plans de symétrie. Nous proposons de faire passer un plan de symétrie comme indiqué sur la figure ci-après :

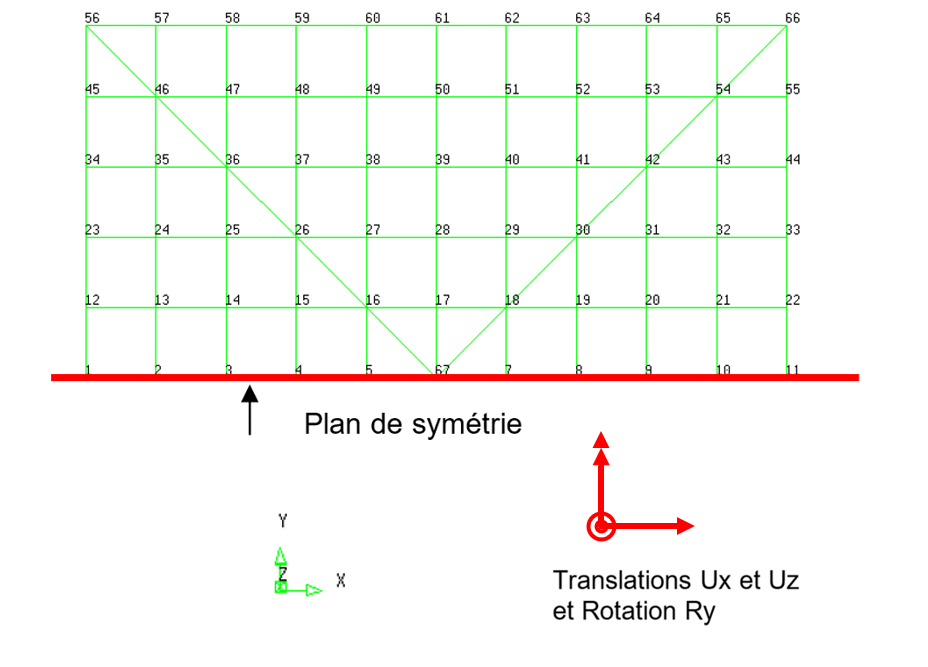
Le radier peut alors être soumis à un chargement qui est soit symétrique, soit antisymétrique.

Par exemple :

Les conditions à appliquer aux nœuds situés sur le plan diffèrent.

Dans le premier cas, les nœuds situés sur le plan de symétrie seront :

Dans le deuxième cas (chargement anti-symétrique), les nœuds situés sur le plan de seront :

Il est important de noter que la prise en compte des différents types de chargements conduit, dans le cas présent, à réaliser deux modèles se différenciant uniquement par les conditions aux limites associées aux chargement, ce qui n’est pas rédhibitoire.

Dans le cas de calculs dynamiques représentant un bloc de sol, on prêtera une attention particulière aux conditions aux frontières latérales du bloc pour traduire correctement les conditions de non-réflexions des ondes (voir Partie 1, chapitre F.8). La définition de ces éléments couplant un ressort et un amortisseur sortent du cadre de ce guide.

© doc Plaxis

C.2.6 Modélisation des fondations

La plupart du temps, le sol est représenté dans les modèles par des conditions d’appui (appuis simples ou encastrements).

Avant de modéliser les fondations et le sol en détail, il faut évaluer la sensibilité de la structure vis-à-vis de la souplesse de ses fondations.

Si la structure y est sensible, on doit prendre en compte le sol :

Dans le cas où la fiabilité des paramètres de sol est faible et/ou leur variabilité forte, il est recommandé d'effectuer un calcul en fourchette.

Dans certains cas, le fait de devoir modéliser la structure avec ses fondations relève d’une obligation règlementaire. Se référer à la norme NF-EN-1998-5 §6.

Pour plus de détail sur les conditions aux limites, on se référera au § C.5 Conditions aux limites.

C.2.7 Modélisation des contreventements par barres

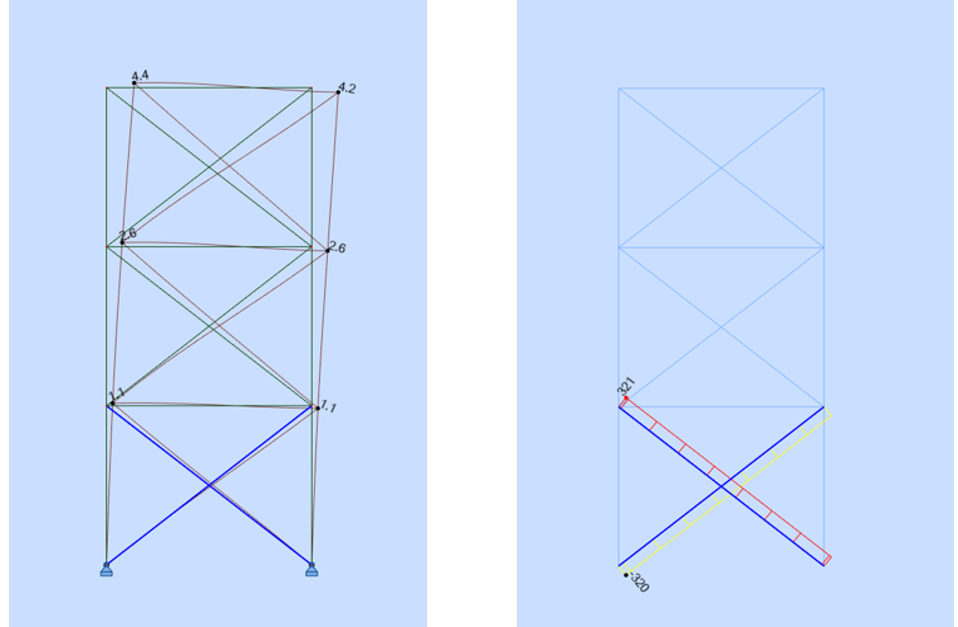
Piège! Dans le cas des structures métalliques, certains éléments très élancés (contreventements ou câbles) ne peuvent travailler qu’en traction. Si la modélisation n’en tient pas compte, la résistance et la raideur du contreventement sont surestimées, aussi bien pour les calculs statiques que modaux.

Illustration par l'exemple sur une structure simple contreventée

Modélisation « tel que construit », avec des barres croisées, mais sans tenir compte du fait que les barres de contreventement vont flamber dès qu’elles vont être mises en compression :

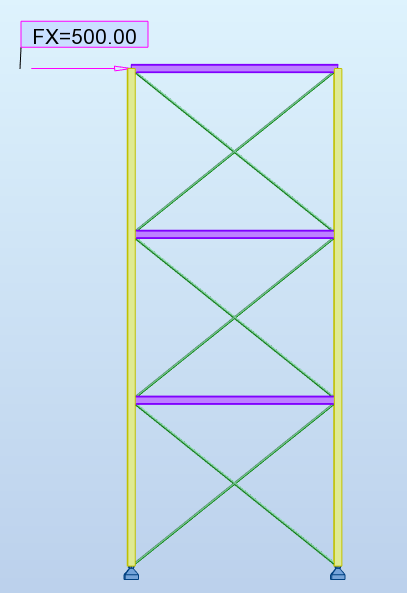
Dans ce cas :

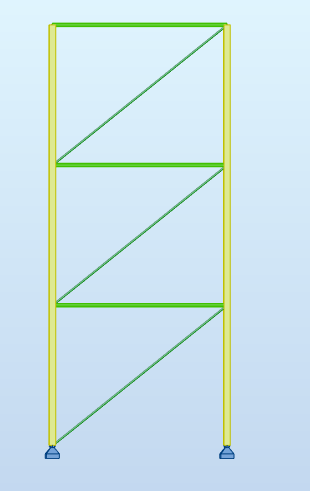
Du fait du flambement des diagonales comprimées, pour le comportement global, il faut supprimer une diagonale sur deux, idéalement celles qui sont comprimées mais ce n’est pas une obligation :

Dans ce cas le déplacement passe de 4.4 à 7.6 cm. La raideur de cette palée est donc divisée par 7.6/4.4=1.73, avec toutes les conséquences que cela peut avoir sur la vérification des déformations et les calculs de périodes propres pour le calcul sismique (Erreur de l’ordre de 1.73^0.5=1.31).

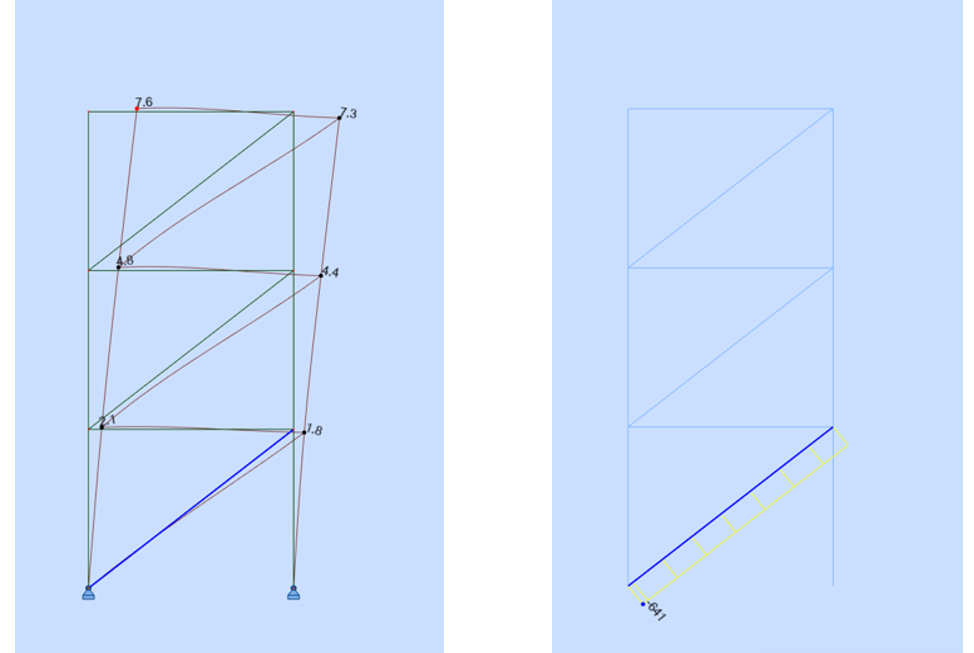
De manière corollaire, les efforts dans les diagonales passent de 321 à 641 kN, soit également de l’ordre du double, en toute logique.

C.2.8 Zoom structurel – Modèle local

Pour des problématiques de fonctionnement local d’un élément ou d’un assemblage d’une structure, il peut être intéressant de bâtir un modèle très local, en lui imposant des conditions aux limites qui reproduisent l’interaction avec le reste de la structure.

C’est par exemple le cas des entretoises de tabliers mixtes, des zones d’appuis des ouvrages complexes ou des encastrements arc/tablier dans un bow‐string.

Il arrive parfois que l’ouvrage soit modélisé dans sa globalité à l’aide d’éléments poutres sauf une partie modélisée à l’aide d’éléments plaques. Dans ce modèle intégrant des éléments de type poutre et plaque, il convient de vérifier attentivement que la transmission des efforts de l’un à l’autre s’effectue convenablement (par exemple en s’assurant de la rigidité suffisante d’éléments fictifs de liaison). Voir C.6.7.

Modélisation globale en éléments poutres (vue pseudo-volumique)

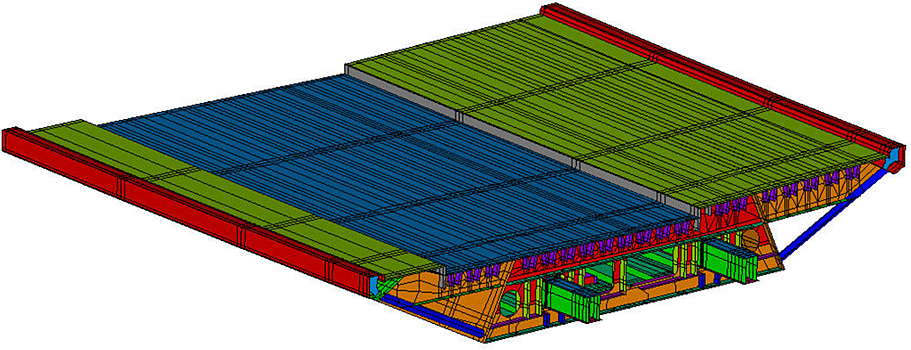
Modélisation locale en éléments plaques (vue des surfaces moyennes)