D.4 Validations réglementaires : comportement en béton armé des éléments
D.4 Validations réglementaires : comportement en béton armé des éléments
D.4.1 Cartographies d’acier – calcul règlementaire BA / bielles
Les calculs des cartographies d’aciers sont réalisés par les logiciels courants en utilisant généralement la méthode de Capra Maury (Annales de l'ITBTP de décembre 1978) ou la méthode de Wood et Armer (The reinforcement of slabs in accordance with a predetermined field of moments » Concrete février 1968, Aout 1968).
Ces méthodes permettent de déterminer les 4 sections d’aciers Axi, Ayi, Axs, Ays sur les faces inférieures et supérieures d’un élément en fonction des 2 directions de ferraillage considérées orthogonales X et Y.
Une bonne approche du calcul de ces cartographies peut être faite à partir de la méthode de Wood en la simplifiant :
Soit un élément soumis aux composantes d’efforts suivantes :
-
Nxx, Nyy, Nxy efforts de membrane (positif si traction) ;
-
Mxx, Myy, Mxy efforts de flexion.
La première étape est de calculer les efforts intermédiaires suivants :
-
Nwx = Nxx + |Nxy| ;
-
Nwy = Nyy + |Nxy| ;
-
Mwx = Mxx + |Mxy| si Mxx est positif sinon Mwx = Mxx - |Mxy| ;
-
Mwy = Myy+ |Mxy| si Myy est positif sinon Mwy = Myy- |Mxy|.
D.4.2 Éléments en flexion : dalles
Les dalles sont principalement sollicitées par les efforts de flexion Mxx, Myy, Mxy.
Les efforts de membranes Nxx, Nyy, Nxy sont souvent négligeables.
Les moments Mxy peuvent être importants, ils sont nuls dans les zones où les moments principaux sont alignés avec les axes principaux (généralement confondus avec les directions du ferraillage) donc en milieu de travée et sur les appuis continus.
Il ne faut pas les négliger surtout dans les angles des dalles et dans le cas de charges concentrées.
Les calculs des aciers passifs réalisés dans la détermination de cartographies sont conformes aux règles de l’Eurocode, car ils se ramènent à l’étude d’une section rectangulaire soumise à un couple de chargement (N, M), ils peuvent donc être réalisés à l’ELS et à l’ELU.
Le calcul des aciers à l’ELS en prenant en compte les ouvertures des fissures est plus délicat et nécessite l’emploi d’un logiciel éprouvé. En effet, la présence des moments MXY nécessite des calculs d’aciers sur plusieurs facettes car la fissuration ne se produit pas nécessairement selon les directions des ferraillages.
Le comportement des dalles en flexion étant conforme à celui des poutres, il est nécessaire de réaliser un décalage des courbes de moment pour respecter le fonctionnement en treillis.
Les sections d’aciers Ax sont calculées directement à partir du couple d’efforts (Nwx, Mwx) et les armatures Ay à partir de (Nwy, Mwy)
Exemple : Dalle carrée de 5 m de côté
La dalle est articulée sur 3 côtés et encastrée sur le 4ème, elle est soumise à une charge permanente uniforme de 50 kN/m², son épaisseur est de 20 cm, l’enrobage des aciers de 3 cm.

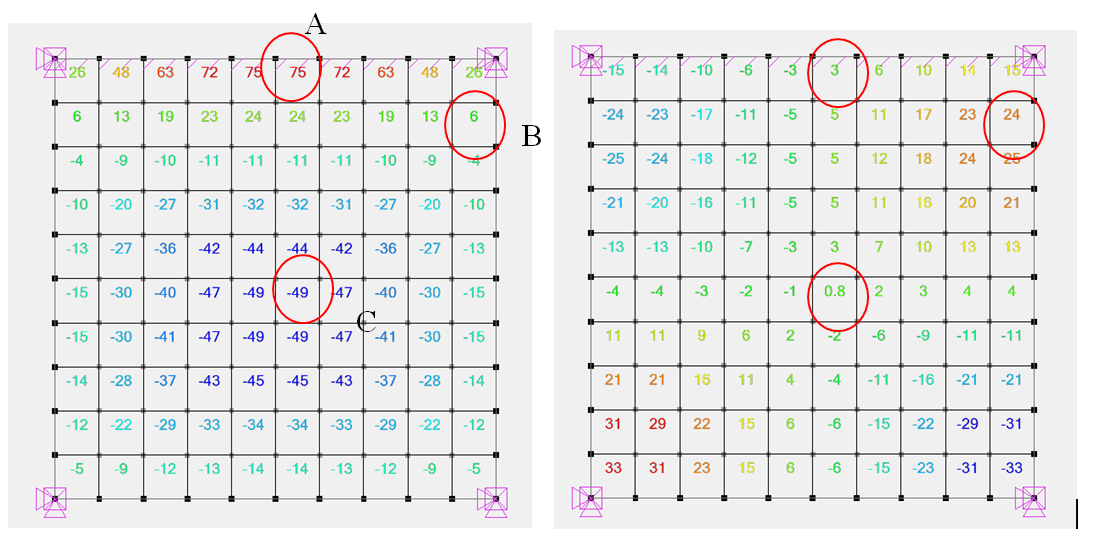
Moments d’axe horizontal MYY | Moments croisés MXY
Les aciers Ay sont calculés manuellement avec fyd=200 MPa (ELS).
| sections : | A | B | C |
| MYY | 75.0 kN.m | 6.0 kN.m | -49.0 kN.m |
| MXY | 3.0 kN.m | 24.0 kN.m | 0.8 kN.m |
| MYY+MXY | 78.0 kN.m | 30.0 kN.m | -49.8 kN.m |
| Ay manuel | 25 cm2 | 10 cm2 | -16 cm2 |
| Ay logiciel | 25 cm2 | 9 cm2 | 17 cm2 |
Ay manuel = 10 x (MYY + MXY)/(0.9 x 0.17 x 200) cm2
Valeurs qui peuvent être comparées avec les sections d’aciers calculées par le logiciel :
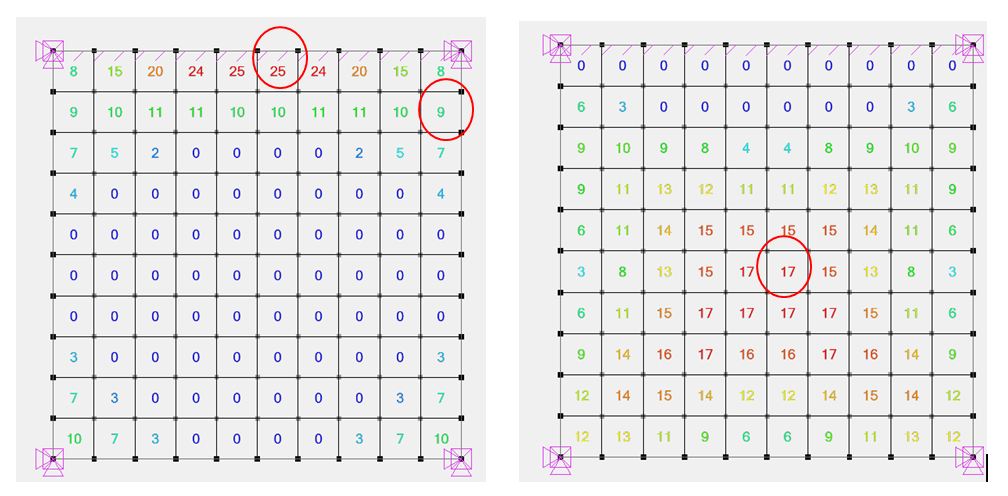
Aciers Ays logiciel / Aciers Ayi logiciel
Il y a une bonne concordance entre les sections d’aciers calculées manuellement et celles déterminées par le logiciel (méthode de CAPRA MAURY).
Il s’en déduit que les moments Mxy se cumulent avec les Moments Mxx et Myy.
D.4.3 Éléments en cisaillement dans leur plan : voiles
Les voiles de contreventement d’un bâtiment sont soumis à des efforts normaux et à des efforts de cisaillements dans leur plan.
Ce sont par exemple les « murs de grandes dimensions en béton peu armé » étudiés dans l’EC8-1 chapitre 5.4.3.5., ou des dalles de transfert de bâtiment soumises à des efforts horizontaux (poteaux inclinés).
Pour ces éléments, les composantes Mxx, Myy, Mxy, Vxz et Vyz sont très faibles voire nulles.
Ils ne sont soumis qu’à des efforts de membrane Nxx, Nyy, Nxy :
-
Nxx et Nyy étant les efforts de traction/compression selon les axes x et y ;
-
Nxy le cisaillement dans le plan du voile.
En reprenant le calcul précédent des cartographies d’aciers, cela donne :
-
Nwx = Nxx + |Nxy| ;
-
Nwy= Nyy + | Nxy|.
D’où les armatures :
-
Ax = (Nxx + |Nxy|)/fyd ;
-
Ay = (Nyy + |Nxy|)/fyd ;
-
Ax et Ay étant la somme des armatures suivant X et Y (2 faces comprises) ;
-
et fyd la contrainte de calcul des aciers.
Ces formules amènent à la constatation que si les efforts normaux sont nuls (Nxx=Nyy=0), alors les armatures Ax et Ay sont des armatures de cisaillements et leurs valeurs sont égales à : Ax= |Nxy|/fyd et Ay= |Nxy|/fyd
Le cisaillement nécessite donc des armatures dans les deux directions, contrairement aux calculs classiques de cisaillement réalisés selon l’EC2. Cela est dû à la non-prise en compte de la résistance du béton.
Les armatures de cisaillements calculées par les cartographies sont donc « supérieures » à celles calculées habituellement en utilisant l’EC2.
On se référera à l’article 5.4.3.5.2 de l’EC8-1 qui concerne l’étude des « murs de grandes dimensions en béton peu armé » qui autorise dans un tel cas de ne pas disposer d’armatures d’effort tranchant si Ved est inférieur à Vrdc.
Il est donc recommandé dans ces cas de n’utiliser les cartographies d’aciers que pour prendre en compte les effets locaux, et de réaliser les calculs des armatures principales en effectuant des coupures à la base des voiles et de déterminer les ferraillages à partir des torseurs résultants au niveau de ces coupures.
Exemple d’un voile :
Etudions un voile isolé de 5 m de hauteur, 4 m de largeur et 20 cm d’épaisseur.
Il est appuyé à sa base, et soumis à une charge horizontale sismique de 2000 kN en tête.
Afin d’éviter les pics d’efforts, la charge horizontale est linéarisée sur la largeur du voile (500 kN/ml).
Voici ci-dessous les efforts de membranes résultants Nxx, Nyy et Nxy.
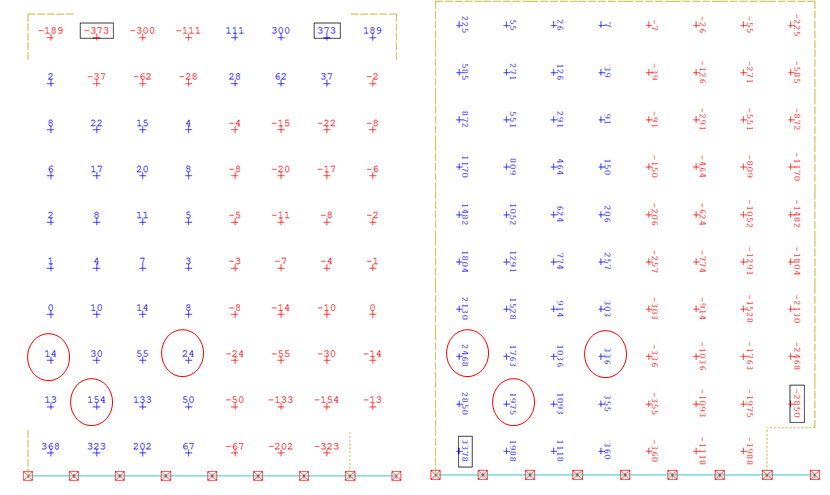
Efforts Nxx (horizontaux)(kN/ml) - Efforts Nyy (verticaux) (kN/ml)
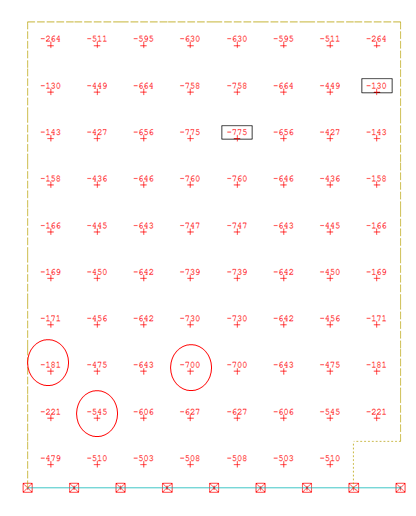
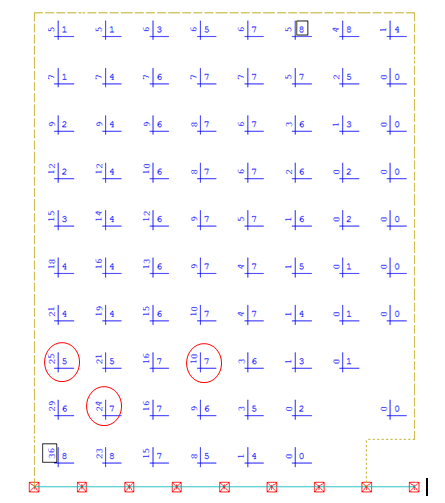
Efforts Nxy (cisaillement) - Cartographies d’aciers (cm²/m²) pour une nappe
Les sections d’aciers sont calculées manuellement et comparées avec les valeurs des cartographies.
| sections : | A | B | C |
| NXX | 14 kN | 154 kN | 24 kN |
| NYY | 2468 kN | 1975 kN | 336 kN |
| NXY | 181 kN | 545 kN | 700 kN |
| NXX+NXY | 195 kN | 699 kN | 724 kN |
| (Axi+Axs) manuel | 4 cm2 | 14 cm2 | 14 cm2 |
| (Axi+Axs) logiciel | 10 cm2 | 14 cm2 | 14 cm2 |
| NYY+NXY | 2649 kN | 2520 kN | 1036 kN |
| (Ayi+Ays) manuel | 53 cm2 | 50 cm2 | 21 cm2 |
| (Ayi+Ays) logiciel | 50 cm2 | 48 cm2 | 20 cm2 |
Ce tableau montre que d’une part le calcul manuel fournit une bonne approximation des sections d’aciers et d’autre part que les efforts de cisaillement Nxy se rajoutent aux deux efforts de membranes Nxx et Nyy, ce qui ne traduit pas la réalité du fonctionnement en béton armé du voile.
Étude réglementaire du voile :
Le voile se recalcule réglementairement selon l’EC2.
Au niveau d’une coupure à la base du voile, les efforts résultants sont égaux à :
-
M-flexion = 2000 x 5 = 10 000 kN.m ;
-
Vu = 2000 kN (ELA).
D’où les aciers de flexion : A-tirant = 10 000 /(0.9 x 3.9 x 50) = 57 cm2 soit 29 cm2 par nappe.

Vrdc = 997 kN est inférieur à Vu = 2000 kN d’où la nécessité de disposer des armatures de cisaillement égales à 11 cm2/ml (soit 6 cm2/ml par nappe) en considérant cot(θ)=1 ou 5 cm2/ml avec cot(θ)=2.5.
Comparaison entre les 2 méthodes :
Les aciers de flexion sont plus importants dans les cartographies car il faut disposer (36+23+15) cm2/ml x 0.5 m= 37 cm2 pour 29 cm2 dans le calcul réglementaire (30% de supplément).
En ce qui concerne les cisaillements , il faut disposer 7 cm2/ml avec les cartographies alors que le calcul réglementaire permet de ne disposer que 2.5 cm2/ml en considérant cot(θ) =2.5.
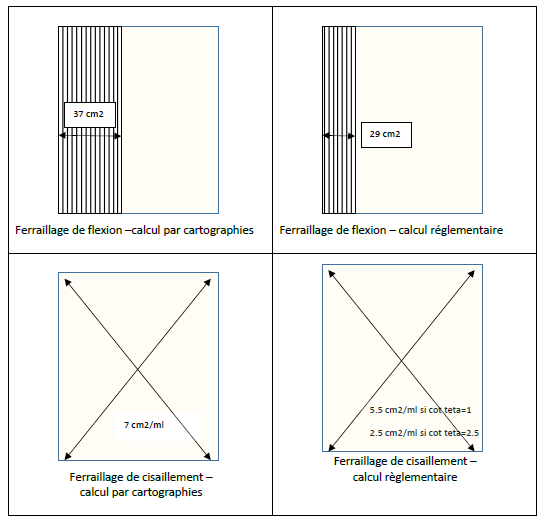
Récapitulatif de la comparaison du calcul d’un voile soit par les cartographies d’aciers soit
par la méthode réglementaire béton armé (EC2)
D.4.4 Méthode des coupures
La majorité des logiciels permettent de réaliser des coupures sur des éléments afin de calculer des torseurs résultants en leurs centres.
Prenons l’exemple de l’étude de la base d’un voile :
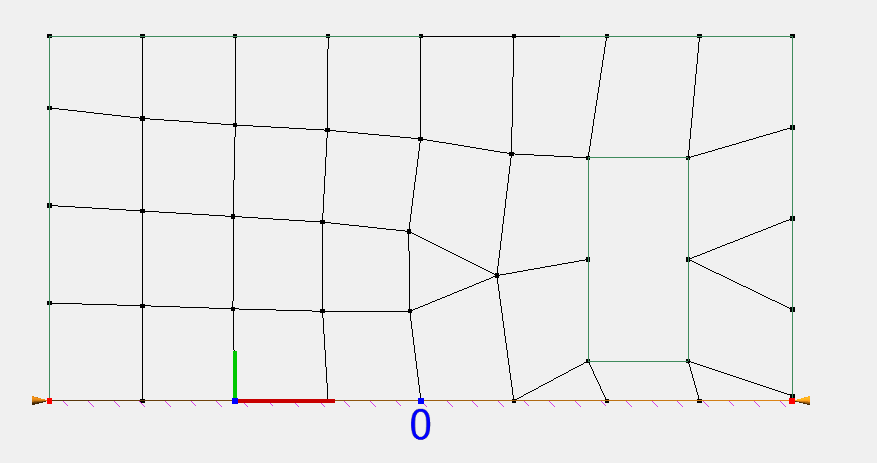
La coupure horizontale au point 0 en base du voile permet d’obtenir le torseur résultant constitué par l’effort normal, le tranchant et le moment (dans le plan ou hors plan), par intégration des contraintes.
Le ferraillage peut alors être déterminé par un calcul type poutre, ce qui implique de s’assurer de rester dans le domaine de définition d’un élément poutre.
L’utilisation des coupures est avant tout très utile à l’ingénieur pour quantifier les cheminements des efforts dans une structure.
D.4.5 Domaine de validité des cartographies d’aciers
D.4.5.1 Cartographies et coupures
Les cartographies d’aciers résultent d’un calcul numérique effectué pour chaque élément indépendamment des autres, donc sans prendre en compte le comportement global en béton armé de la structure.
Nota : La méthode des coupures est la seule respectant le fonctionnement des voiles en béton armé et considérée comme réglementaire. Les compléments usuels sont à appliquer : décalage de la courbe des moments, vérifications des bielles, chaînages et ferraillage minimal … restent à faire.
Il importe donc à l’ingénieur de valider par d’autres méthodes réglementaires les résultats obtenus.
Exemple d’une poutre voile calculé avec la cartographie :
L’exemple d’une poutre sur deux appuis est étudié ici. La poutre est modélisée comme un voile de grande hauteur, pour montrer sur un cas simple les incohérences des cartographies d’aciers.
Soit la poutre isostatique de 10 m de portée, 3 m de hauteur et soumise à une charge uniforme de 200 kN/m2. Cette poutre est modélisée en éléments de plaques travaillant dans leur plan avec un maillage 0.5 x 0.5 m².
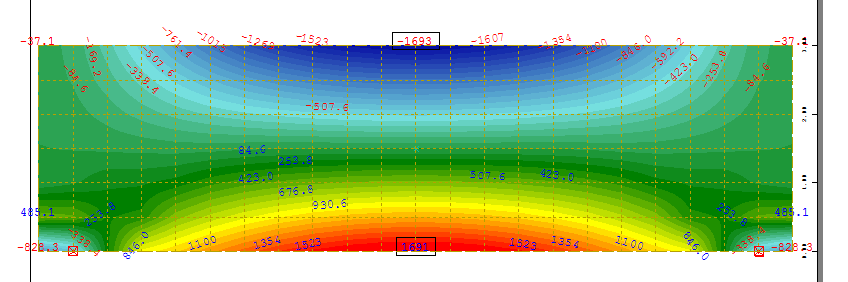
Visualisation des efforts horizontaux Fxx
Calcul du ferraillage à partir des cartographies d’aciers :
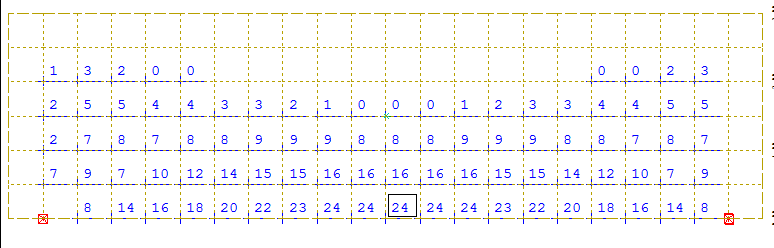
La capacité de flexion est égale à F0 x d0 = 2 nappes x 0.5 m x (24 x 2.75 + 16 x 2.25 + 8 x 1.75) = 116 cm2.m
Le ferraillage à disposer est égal à Ax = 116 cm2.m / 2.9 m = 40 cm2
Calcul du ferraillage à partir des coupures :
Une deuxième méthode consiste à réaliser une coupure au milieu de la poutre (A-A).

Le logiciel intègre les efforts Fxx sur la hauteur de la coupure pour en déduire le torseur résultant au milieu de la coupure.

Le moment au centre est égal à 3358 kN.m, (on retrouve alors le moment classique RDM Mu=1.35ql2/8 = 3375 kN.m), d’où le ferraillage calculé selon les règles du béton armé : A = 3358/(0.9 x 2.9 x 43) = 30 cm2
Conclusion et comparaison des deux méthodes :
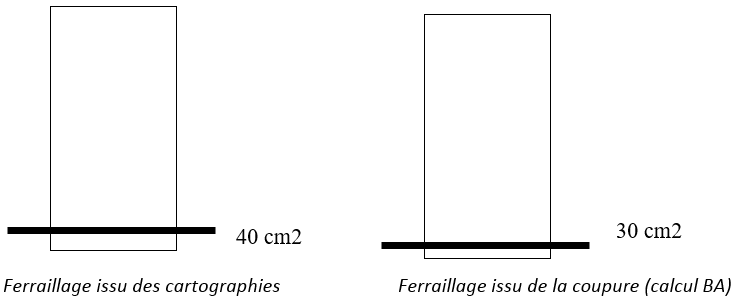
Ferraillage issu des cartographies / Ferraillage issu de la coupure (calcul BA)
Conclusion : Cet exemple montre les limites des cartographies d’acier, car la méthode ne respecte pas la règle des déformations du béton armé. La méthode des coupures permet d'optimiser les ferraillages.
D.4.5.2 Méthode des bielles: apport des éléments finis
Cas d’une poutre-voile (ou poutre cloison)
L’Eurocode 2 encourage fortement l’utilisation de la méthode des bielles, dans ce cas les éléments finis peuvent aider l’ingénieur à définir le schéma de fonctionnement des bielles ainsi que les inclinaisons des bielles. Considérons l’exemple de la poutre-voile suivante :
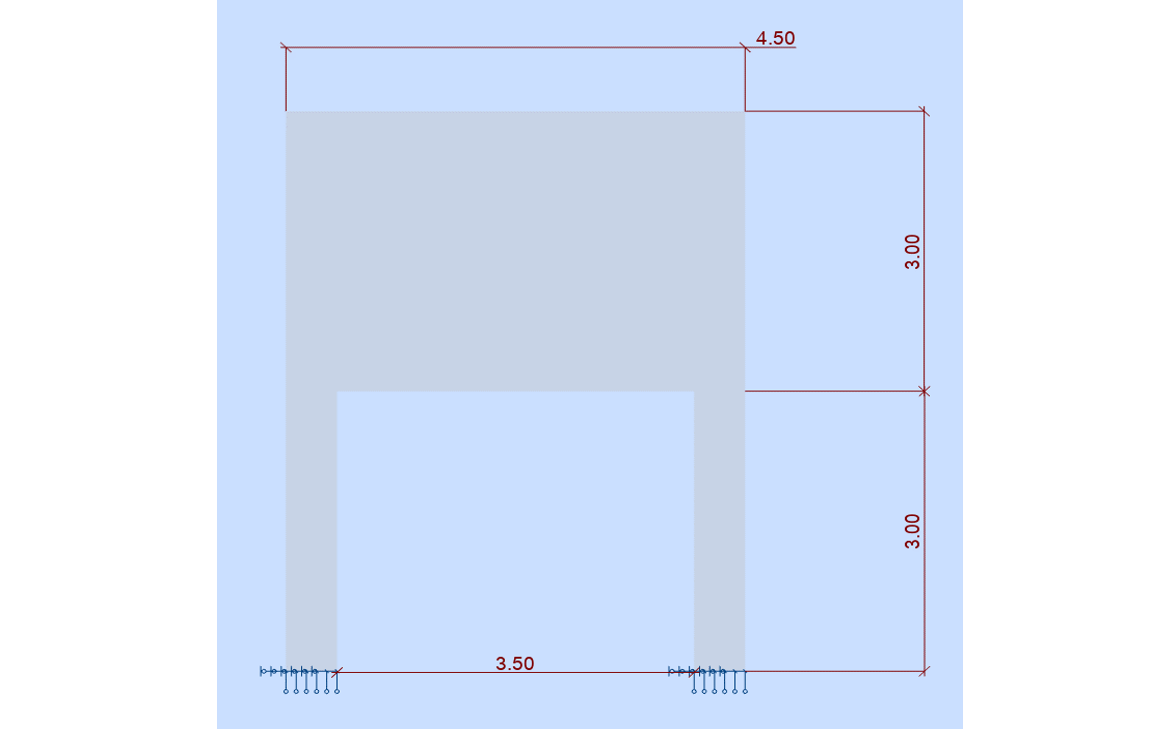
La portée de 3m50 étant inférieure à 3 fois la hauteur de la poutre, les règles classiques des poutres ne s’appliquent pas (EC2-5.3.1), ce voile se calcule par la méthode des bielles.
Cet exemple étant assez simple, nous pouvons définir manuellement le fonctionnement en bielle :
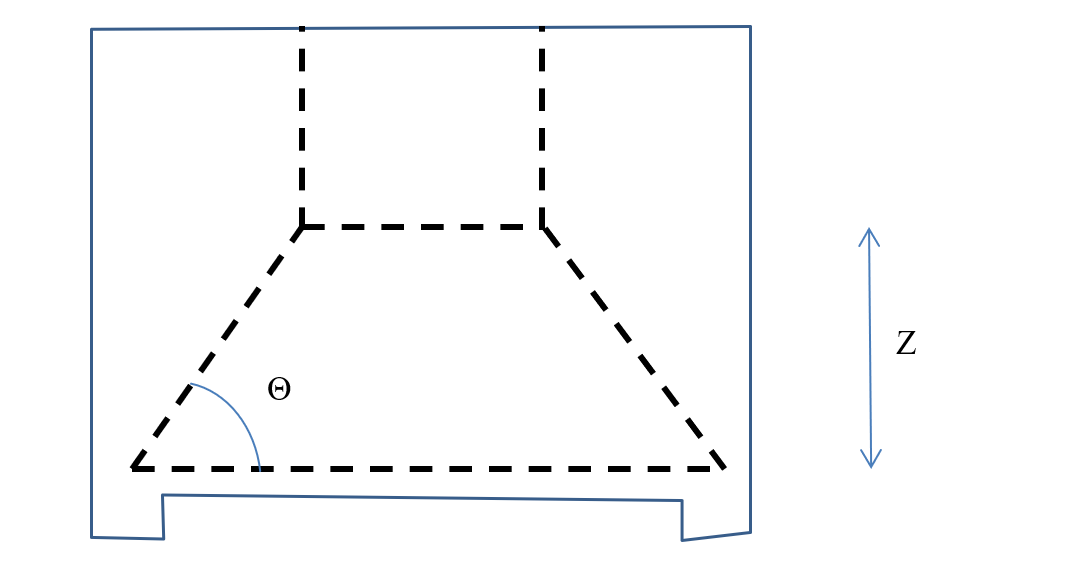
Les règles usuelles estiment la hauteur de la bielle Z à 1.90 m , nous obtenons tgt (Θ) = 2.18, soit un tirant inférieur H=515 KN , soit une section d’acier théorique A=11.8 cm² (calcul ELU).
Dans les cas plus complexes, l’ingénieur devra définir un fonctionnement en bielles qui pourra s’avérer difficile. Les éléments finis apportent alors une aide précieuse pour l’ingénieur, nous proposons à l'ingénieur de suivre la méthode suivante:
Modèle isolé représentatif :
Le principe consiste à réaliser un modèle isolé représentatif du problème.
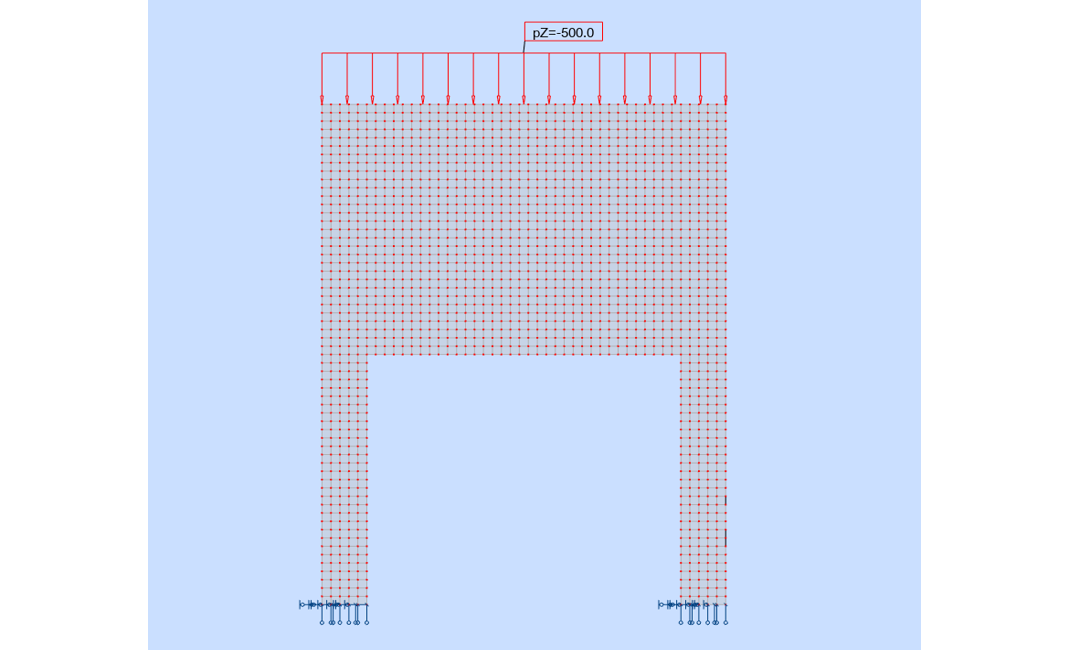
Modèle isolé représentatif
Les contraintes principales :
On se référera aussi à la partie 1 chapitre E.3.3.
Ce qu’il faut retenir : Il y a 2 contraintes principales, la mini S1, la maxi S2, elles sont représentées sous forme de flèches perpendiculaires, la longueur de chaque flèche dépendant de l’intensité de la contrainte. La contrainte S1 visualise les compressions négatives et S2 les tractions positives.
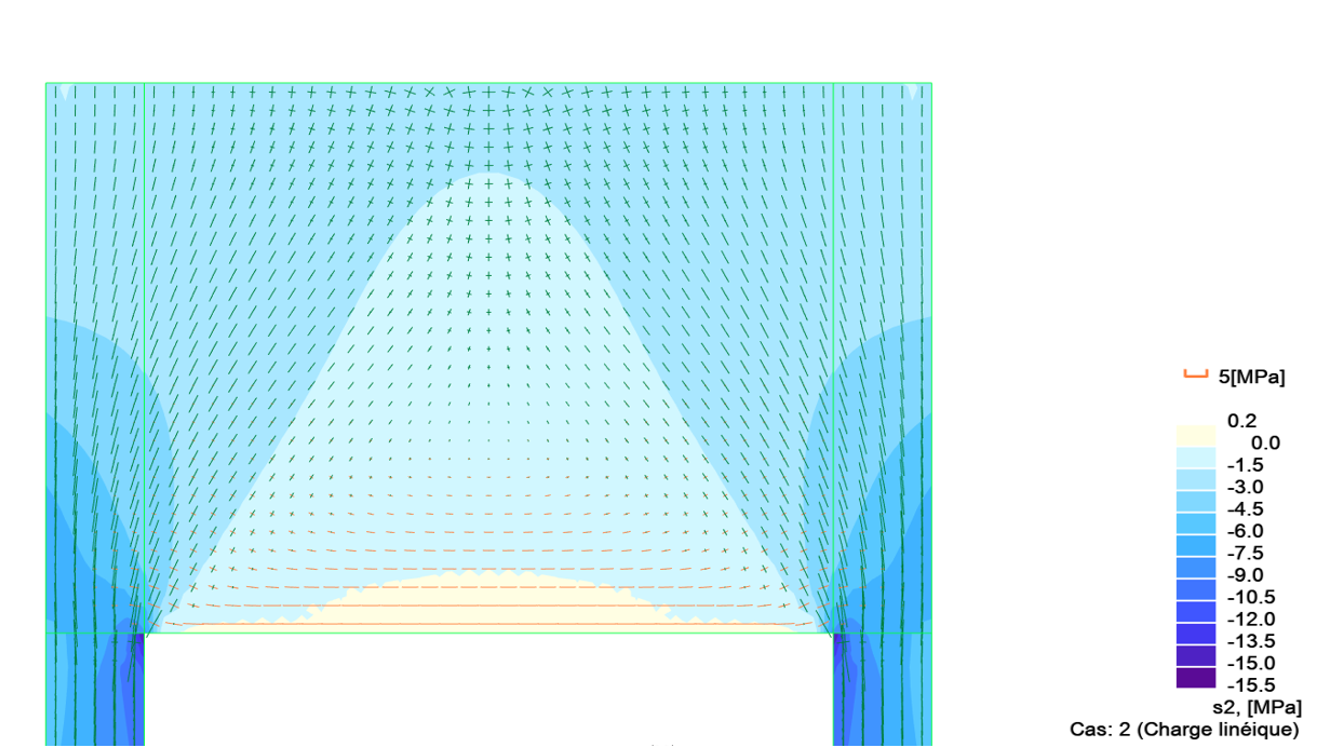
Contraintes principales S2 (compressions)
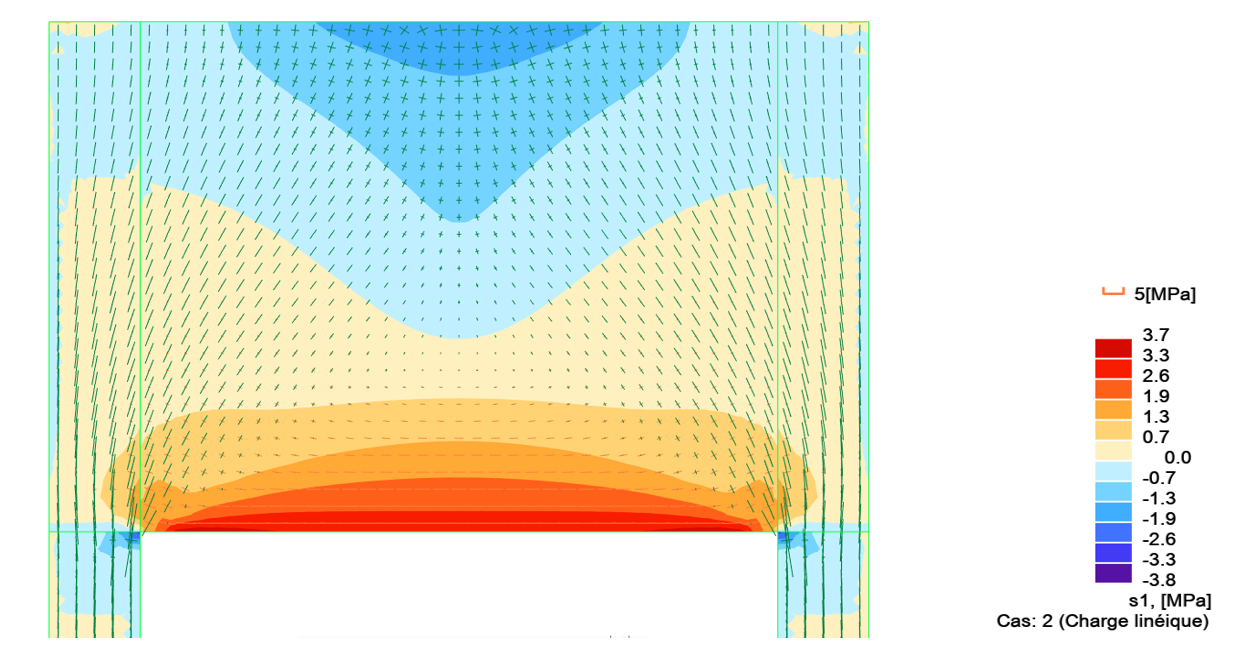
Contraintes principales S1 (tractions)
Dans notre cas, les longues flèches bleues montrent des zones de compression, les rouges montrent les zones de traction.
A savoir aussi : lorsque les 2 flèches S1 et S2 sont quasiment égales, c’est-à-dire lorsque la représentation est une croix, alors la zone est en cisaillement pur.
Définition du fonctionnement en bielles :
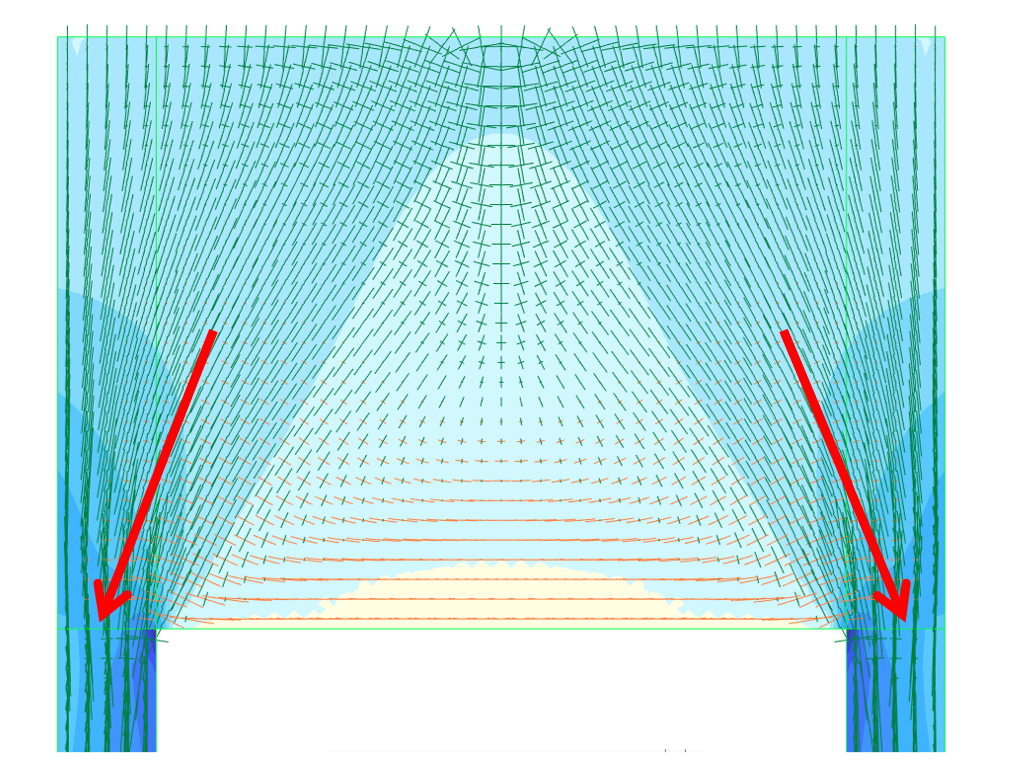
La visualisation des contraintes de compression à la base permet de visualiser la direction de la bielle, sont angle est de l’ordre tgt(Θ)= 2. Soit un tirant de 562 KN d’où une section d’acier A = 13 cm² avec quand même une incertitude due à la méthode graphique.
Cartographies d’aciers :
Les cartographies d’aciers donnent directement le ferraillage du tirant inférieur :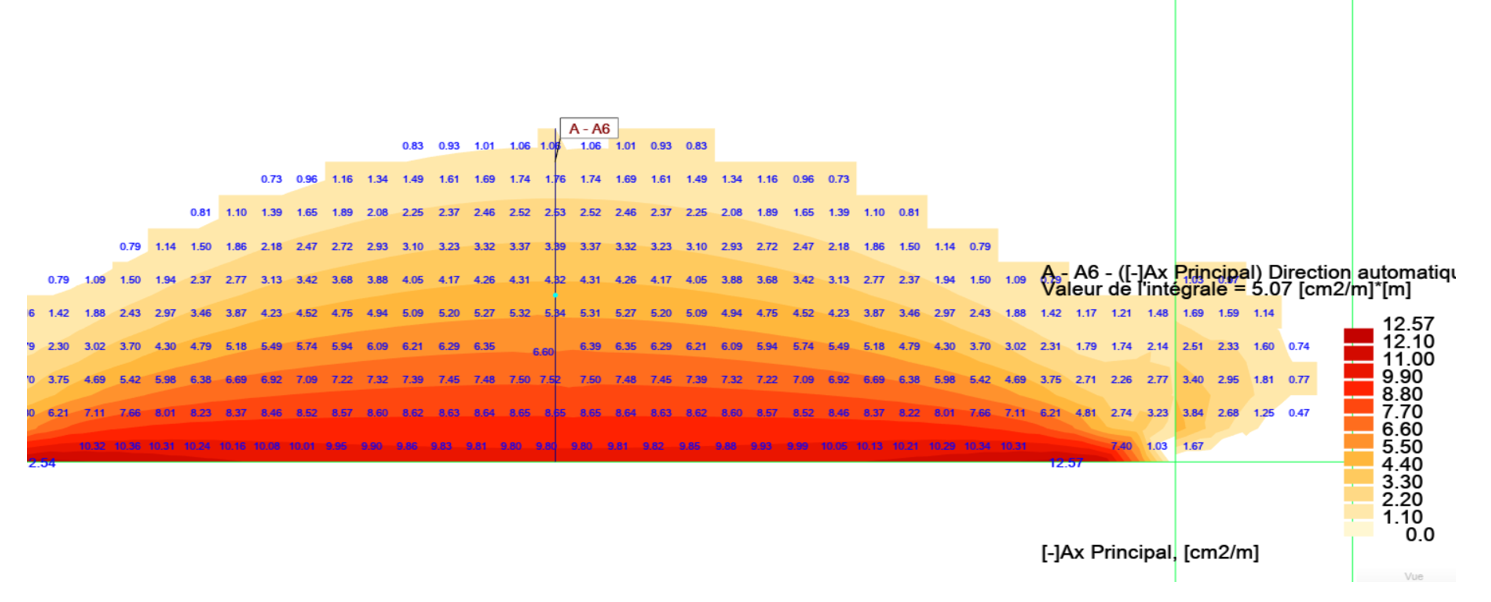
L’intégrale des sections d’acier sur 1 m donne un ferraillage de 5.07 cm² par nappe soit 10 cm² au total. Cette valeur plus précise pourra être retenue.
Bilan
Cette approche permet de bien cerner le cheminement des efforts et de monter un modèle de bielle tirant adéquat (compatible avec le cheminement des efforts).

Cheminement des efforts dans le cas d'ouvertures multiples, contraintes S1

Cheminement des efforts dans le cas d'ouvertures multiples, contraintes S2
Le lecteur se reportera utilement au §8 “Strut-and-tie modelling” du bulletin n°45 de la fib pour obtenir les détails de modélisation de ce genre d'approche et au Bulletin Ouvrage d'Art n°14 du SETRA, pages 23 à 32.