C.16 Compléments liés aux calculs dynamiques et sismiques

Les sollicitations dynamiques engendrent des efforts inertiels et cinématiques dans la structure.

Si l'on effectue un dimensionnement suivant l'Eurocode 8, ce dernier fournit une explication détaillée des simplifications admissibles, dans la modélisation et dans le calcul, selon la régularité de la structure. Cette notion de régularité est explicitée au §4.2.3 de l’EN1998-1. Pour les ponts, le guide « Ponts courants en zone sismique » fournit également des critères de régularité et les simplifications de calcul admissibles.

Selon la sophistication du modèle et les objectifs recherchés, plusieurs points de vigilance sont à envisager.

C.16.1 Définition des axes généraux X et Y

La définition des axes généraux X et Y demande une attention particulière, car les résultats sismiques peuvent être erronés si ces axes ne sont pas proches des axes principaux d’inerties de la structure.

Nous indiquons ci-après 2 exemples visualisant ce sujet.

Exemple: Bloc d’angle d’un stade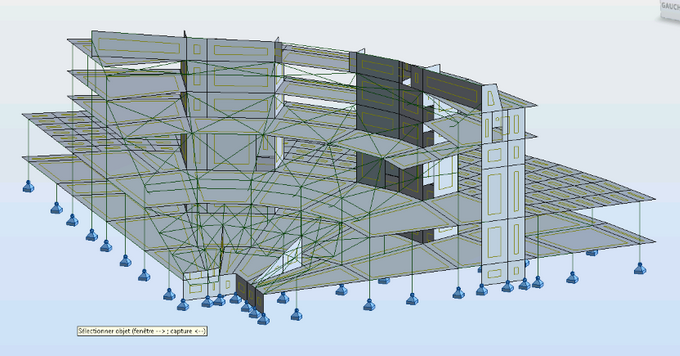

Vue d'ensemble du modèle du bloc d'angle

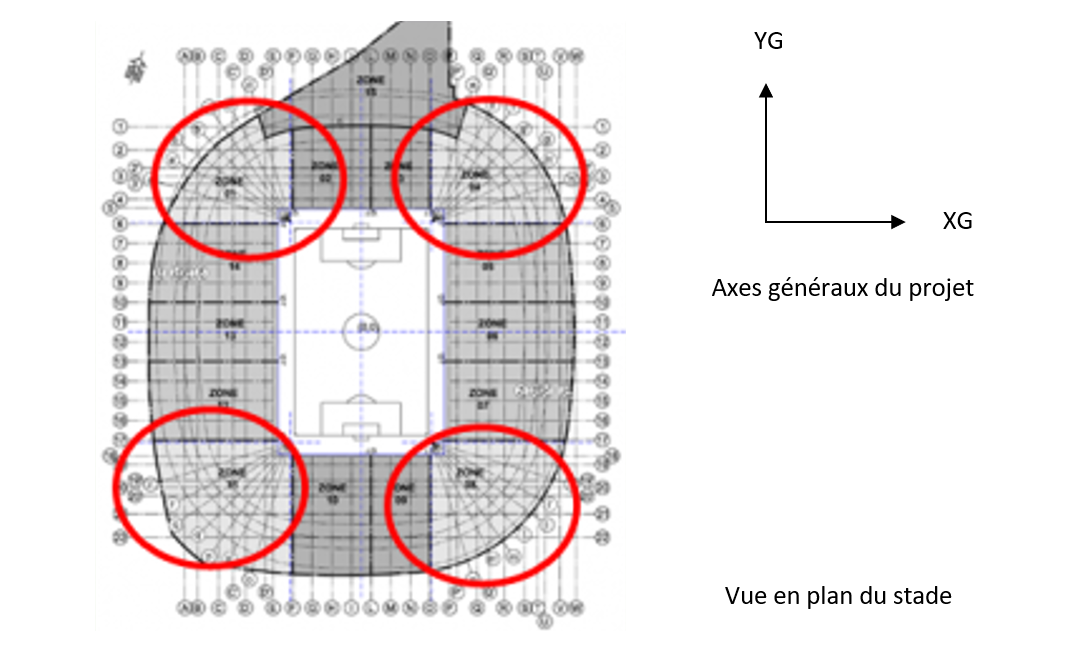
Il est nécessaire d’adopter pour les blocs d’angles des axes de description (X,Y) différents de ceux du projet général (XG,YG). L’axe X doit être radial dans le sens du 1er mode de vibration.

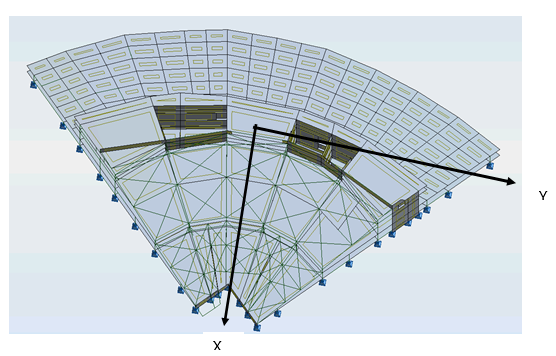
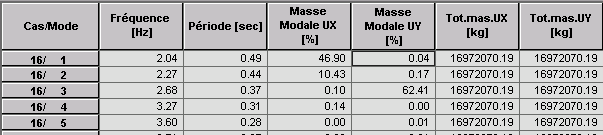
L'étude des modes propres montre alors que l'on retrouve les modes fondamentaux d'un bâtiment classique avec des modes bien différenciés selon les directions X et Y et un mode de torsion ce qui ne serait pas le cas en adoptant les axes généraux XG, YG, car chaque mode entraînerait des masses selon les 2 directions, ce qui perturberait les combinaisons CQC et celles de Newmark.

Exemple : Séisme sur un pont courbe

Dans l’exemple ci-après, deux calculs sismiques ont été réalisés pour ce viaduc TGV présentant une courbure en plan.

Le premier selon les axes généraux X et Y orientés selon la culée de gauche et le deuxième avec des axes orientés selon la culée de droite.

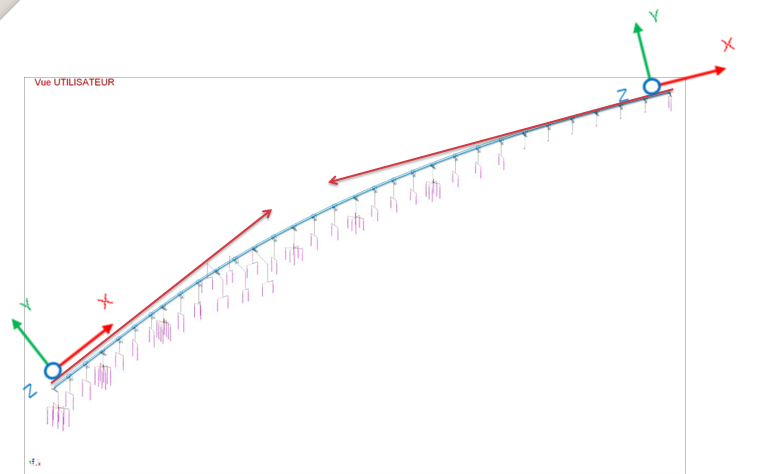
Le passage d’un modèle à un autre est réalisé en modifiant les coordonnées des nœuds du modèle. La comparaison des efforts à la base des appuis met en évidence des résultats très différents entre les 2 modèles.

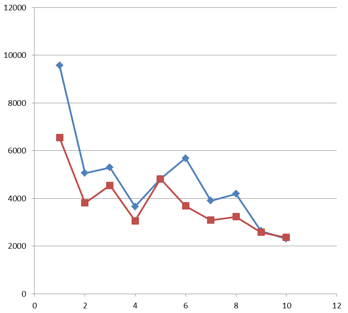
Graphique n° appui/effort en pied (kN)

Il est donc conseillé de réaliser les calculs sismiques des ponts sur des tracés droits en plan si la courbure le permet (se référer aux guides CEREMA), sinon, il faut réaliser plusieurs calculs en faisant varier les axes pour chaque appui étudié, solution complexe à éviter de préférence.

C.16.2 Modélisation des éléments non structuraux ou secondaires

Voir C.4 Modélisation des éléments non structuraux ou des équipements.

Les éléments non structuraux et les équipements n’ont pas à être modélisés si leur masse reste faible par rapport à celle du bâtiment. Cependant, il faut s’assurer que leur raideur n’influence pas le comportement de la structure. Dans le cas contraire, il faut les prendre en compte. Pour un complément d'information, on peut se référer au §2.4.5.2 du guide de l’ASN et au cahier technique 36 de l’AFPS concernant le dimensionnement des éléments non structuraux sous séisme.

La masse de ces éléments non structuraux devra être définie correctement dans l’espace, lorsqu’elle n’est pas négligeable. Par exemple, le décalage des masses des éléments latéraux des ponts par rapport au centre des sections devra être bien défini pour prise en compte dans les modes de torsion.

La répartition des masses sur les planchers peut engendrer de nombreux modes locaux lors d’une analyse modale et rendre difficile l’exploitation du modèle. Il est recommandé, dans ce cas, de privilégier des masses ponctuelles et de refaire une étude locale si besoin.

C.16.3 Transformation des charges en masse

La majorité des logiciels calculent directement le poids de la structure ou possèdent une option pour le faire sur la base de la densité ou du poids volumique des matériaux.

Pour les calculs sismiques et dynamiques, il faut veiller à ce que les poids, forces et pressions soient convertis en masses avec la pondération règlementaire (cas des équipements et superstructures ou d’une partie des charges d’exploitation).

Pour réduire le nombre de modes propres non utiles à un calcul global, on peut privilégier les options qui transforment les masses réparties en masses aux nœuds ou introduire soi-même les masses ajoutées à la main, aux nœuds.

C.16.4 Attention à la cohérence des unités

La justesse des calculs sismiques ou dynamiques est particulièrement sensible à la cohérence des unités. Les forces d’inerties font intervenir l’accélération de la pesanteur g, dont l’unité (généralement définie par défaut) doit être cohérente avec toutes les autres.

Trivial, mais il est toujours utile de rappeler que l'unité de masse est … le kilogramme.

On sera particulièrement vigilant dans le cadre de l’utilisation d’anciennes normes ou règlements, pouvant employer des unités telles que le kgf (kilogramme force). De manière générale, il est conseillé de privilégier l’utilisation stricte des unités système international, a minima pour le contrôle des résultats.

Prenons l’exemple simple du calcul du poids propre. Pour la plupart des logiciels, l’action de la pesanteur est définie par l'application d’une accélération verticale appliquée à l’ensemble de la structure. En interne, le logiciel va calculer la masse de la structure en calculant au préalable pour chaque élément son volume multiplié par la densité de son matériau. Si on désire obtenir le poids propre en N et que les dimensions géométriques et la densité ont été définies respectivement en mm et en kg/mm³, l’accélération devra être définie en… m/s²:

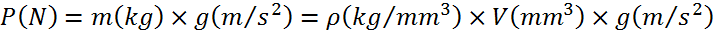
Par exemple la masse équivalente à une surcharge d'exploitation de 20 KN est égale à 20 000 (N)/ 9.81 (m/s²) = 2038 Kg soit 2.038 tonnes.

C.16.5 Matériaux

Les lois des matériaux ainsi que les coefficients partiels dépendent du type d’analyse effectué.

En béton, par exemple, le module d’Young instantané sera privilégié.

Pour tenir compte de l’état de fissuration des éléments, le module EI peut être modifié :

soit par un coefficient minorateur appliqué sur le module d’Young E;
soit par modification de la section résistante ou de l’inerte directement.

Le référentiel appliqué peut préciser le coefficient de Poisson à appliquer en fonction du type de calcul. Celui-ci pourra être modifié pour tenir compte de l’état de fissuration, par exemple, égal à zéro dans le cas d’un élément fissuré ou sous séisme ELA.

C.16.6 Modélisation des éléments de contreventements des structures métalliques

Les éléments de contreventement assurent la stabilité latérale de la structure. Il est important de traduire leur fonctionnement réel. Par exemple, pour des Croix de Saint-André, les barres ne travaillent qu’en traction, leur mise en compression entraînant leur flambement, instantanément. Les croix ne doivent donc pas être modélisées en totalité si un calcul linéaire est prévu. Dans le cas contraire, on surestimerait la capacité des contreventements avec un facteur de l'ordre de 2. Voir C.2 Modélisation des éléments principaux

C.16.7 Conditions aux limites

Selon les modèles, la prise en compte de l’interaction sol-structure dynamique peut être nécessaire. Il est nécessaire de s’assurer que la structure ne se soulève pas de manière exagérée pour rester dans le domaine de validité d’une étude linéaire si les ressorts sont modélisés de la sorte.

Pour les études sous séisme, l’ingénieur peut calculer les raideurs en se référant aux documents suivants :

« Ponts en zone sismique » édité par le CEREMA qui propose au chapitre 4.3.3.2 des formules de calculs assez simples;
Conception-construction parasismique - V. Davidovici §4.3.4.4 Modélisation du sol par un système de ressorts amortis - Collection Eurocode - Afnor Editions;
Formules de Gazetas : que l’on peut consulter dans l’annexe D de « Fondations et procédés d’amélioration du sol de Davidovici » (ou autres références).

Tous ces documents déterminent les raideurs à partir des modules de cisaillement et des coefficients de Poisson des sols, mais également des dimensions caractéristiques de la fondation. Ces raideurs dépendent des fréquences de vibration de la structure étudiée.

Cas des radiers :

La modélisation d’un radier sous chargement dynamique est plus complexe, car les ressorts devront représenter à la fois les raideurs verticales, horizontales et en rotation, déterminées par l’étude d’interaction sol-structure.

On se référera aux documents spécifiques à ce type d’études.

Plusieurs formes de modélisation sont possibles :

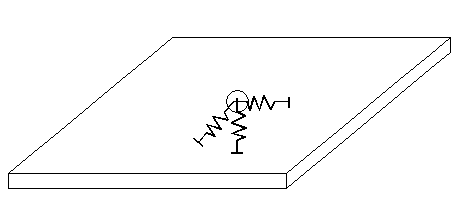
par un ressort ponctuel au centre du radier affecté des 6 raideurs (et 6 amortissements), avec des liaisons rigides sur tous les nœuds du radier;

Avantage : une représentation fidèle de l’ISS dans les calculs dynamiques.

Inconvénient : il n’est pas possible de déterminer les efforts dans le radier du fait de la présence des liaisons rigides qui rigidifient artificiellement le radier. Il faut alors procéder à un calcul local du radier soumis aux pressions de sols déduites des efforts dans le ressort central. En particulier, dans le cas d’un radier de grandes dimensions par rapport à son épaisseur, cette méthode n’est pas adaptée.

par des ressorts placés uniformément sous le radier (comme pour l’étude statique);

Dans ce cas chaque nœud du radier est relié à 3 ressorts, un dans chaque direction X, Y, Z.

Les ressorts horizontaux selon X ou Y seront déduits directement des raideurs globales en translation, par contre les raideurs des ressorts verticaux devront représenter soit la raideur verticale globale, soit la raideur en rotation globale dans une direction donnée. Cette approche implique 3 modèles de calcul pour analyser les 3 directions de séisme.

Avantage : une modélisation plus simple, permettant de calculer les efforts dans le radier.

Inconvénient : une des 2 raideurs verticales ou en rotation n’est pas représentée dans chacun des modèles de calcul. La raideur en torsion n’est de fait pas intégrée.

par la mise en place d’un matelas de ressorts;

Ce type de modélisation est surtout utilisé dans les structures complexes, un matelas de ressorts affectés à chaque nœud du radier permet de représenter toutes les raideurs globales.

Avantage : l’ISS est modélisée finement.

Inconvénient : la modélisation est complexe et ne peut être appliquée qu’en utilisant des logiciels spécifiques en connaissance de cause.

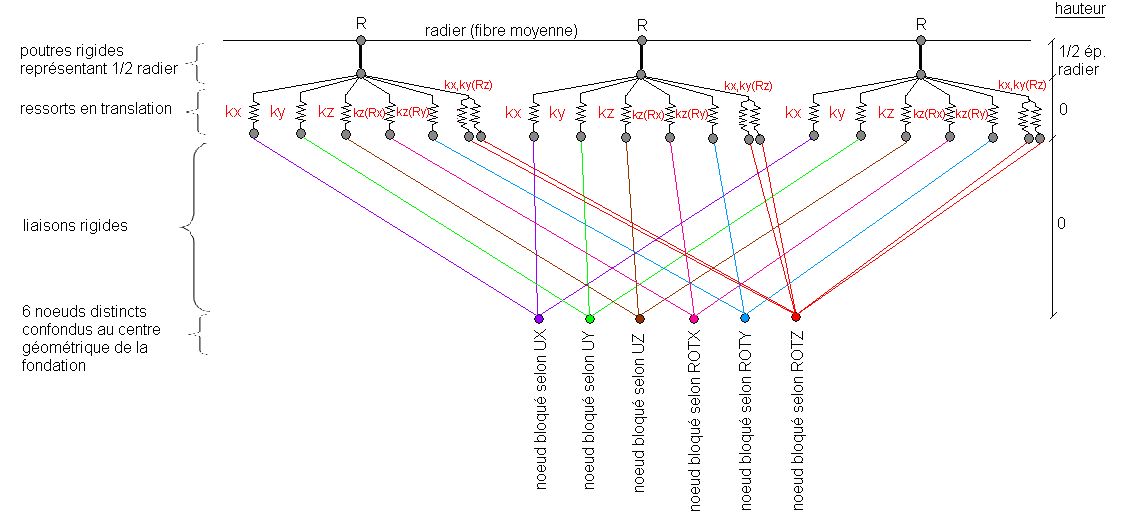
Figure : Schématisation du matelas de ressorts, image Tractebel

Troncature – nombre de modes

La notion théorique de troncature est définie dans la partie 1 de ce guide. En pratique, concernant le nombre de modes à retenir pour le calcul, on conseillera :

de ne pas dépasser 100 modes pour les ouvrages classiques;
d'aller jusqu’à la fréquence de coupure (généralement 33 Hz);
de faire appel à un pseudo mode pour la masse participante non prise en compte (EN 1998-2/§4.2.1.2);
de ne pas se limiter aux modes ayant le plus de masses participantes, car les modes antisymétriques ont classiquement une masse participante très basse mais induisent des efforts non nuls;
de réfléchir à la pertinence de retenir ou non dans l’analyse, les modes locaux.

Coefficients de comportement

Le coefficient ou plutôt les coefficients de comportement, puisqu'ils peuvent être différents dans chaque direction, sont intégrés dans la définition des spectres de calcul. Attention à vérifier que les déplacements calculés sont bien remultipliés par ce même coefficient.

Signature des modes

A l’issue de la combinaison des réponses spectrales, le signe des efforts est perdu (toutes les valeurs sont positives). Ceci peut générer des difficultés d’exploitation lorsque l’on souhaite calculer un torseur ou que l’on souhaite étudier des efforts concomitants (cf. D 7.4.5).

Pour réattribuer un signe aux différentes quantités calculées, il existe plusieurs approches possibles dont celles décrites ci-dessous :

Attribution du signe d’un des modes. Pour les structures ayant un mode prépondérant dans chaque direction, il est possible d’assigner le signe du mode prépondérant aux quantités calculées. Ceci est intéressant pour le comportement global de la structure et s’avère très efficace tant que la participation de ce mode est supérieur à 60% de la masse modale de la structure. Par contre, pour les éléments répondant sur des modes locaux plus élevés, ceci peut ne pas être approprié (cf. exemple de planchers épais dans des sites industriels);
Attribution du signe suite à une analyse d’accélération uniforme. Pour chaque direction, on applique une accélération unitaire et on retient le signe obtenu;
Analyse par la méthode des ellipses. Lorsque la justification d’un élément structurel doit prendre en compte plusieurs composantes de sollicitations, il est loisible d’établir le domaine de concomitance de ces grandeurs, pour ne pas introduire de conservatisme dans le calcul.

C.16.9 Amortissement

Dans le cadre d'une étude de structure avec un spectre de calcul comportant un coefficient de comportement, ce dernier tient déjà compte de l’amortissement. Il ne faut pas vouloir chercher à en rajouter un autre.

Si on est dans le cadre d'un dimensionnement à l'aide d'un spectre de réponse élastique, il faut retenir les amortissements des matériaux.

On veillera dans la mise en données à ce que l’amortissement des matériaux compris ou pris par défaut par le logiciel soient cohérents avec le règlement et l’analyse menée. Par exemple, il est nécessaire de distinguer le béton armé du béton précontraint, ou encore les charpentes soudées des charpentes boulonnées dans la définition des amortissements des matériaux.

C.16.10 Schéma d’intégration en temps et discrétisation

La résolution d’une sollicitation dynamique nécessite la mise en œuvre d’une méthode d’intégration spécifique. Le chapitre 2 de la partie 1 fournit des détails sur ces méthodes et des indications pour choisir le pas de temps et le maillage en fonction du problème à résoudre. Il convient de faire appel à des ingénieurs spécialistes de ce type d’étude.