MODÉLISATIONS ET CALCULS AUX ÉLÉMENTS FINIS DANS LE DOMAINE DU GÉNIE CIVIL
Le site connaît actuellement quelques perturbations. En attendant son rétablissement, une version pdf est disponible ici, scindée en plusieurs parties à recombiner . Copiez les liens ci-dessous dans un navigateur. - https://www.afgc.asso.fr/partie0/ - https://www.afgc.asso.fr/partie1/ - https://www.afgc.asso.fr/partie2_1/ - https://www.afgc.asso.fr/partie2_2a/ - https://www.afgc.asso.fr/partie2_2b/ - https://www.afgc.asso.fr/partie3a/ - https://www.afgc.asso.fr/partie3b/
- Table des matières
- L'édito AFGC
- Le calcul aux éléments finis – un changement de paradigme
- Préface - Le mot du Conseil Scientifique et Technique
- Préambule
- Contenu des Recommandations et Conseils - Les auteurs
- Laissez nous vos commentaires pour nous permettre d'améliorer le site
- Introduction
- PARTIE 1 - ÉLÉMENTS THÉORIQUES
- Chapitre A. Généralités
- A1. Formulation générale pour les calculs élastiques linéaires
- A2. Dimensionalité de la modélisation
- A3. Choix des éléments finis
- A.4. Interaction entre la structure et son environnement
- A.5. Estimation de la qualité de la solution numérique approchée
- Chapitre B. Dynamique
- B.1 Analyses reposant sur une recherche modale
- B.2 Analyses reposant sur une intégration temporelle directe
- B.3 Prise en compte de l'amortissement
- B.4 Spécificités de l'analyse sismique
- Chapitre C - Calculs statiques non-linéaires
- C.1 Les problèmes de mécanique non-linéaires
- C.2 Pourquoi exécuter des calculs non-linéaires ?
- C.3 Mise en œuvre
- C.4 Problèmes de convergence ? Symptômes et solutions
- Chapitre D - Génie civil
- D.1 Les matériaux du génie civil
- D.2 Les catégories d'éléments d'ouvrage
- D.3 Les phases de construction
- Chapitre E - Post-traitements typiques du génie civil
- E.1 Généralités
- E.2 Grandeurs en dynamique
- E.3 Cas spécifique du béton armé
- Chapitre F - Calculs géotechniques
- F.1 Aspects géométriques
- F.2 Non-linéarités matérielles
- F.3 Interactions sol-structure
- F.4 Effets hydrauliques
- F.5 Incertitudes et recommandations
- F.6 Aspects normatifs : Principes de l'Eurocode 7
- F.7 Modélisation en dynamique
- F.8 Échelles caractéristiques
- PARTIE 2 - ÉLÉMENTS PRATIQUES
- Chapitre A. Comprendre les éléments finis
- A.1 Que fait le logiciel dans un calcul aux éléments finis? Exemple des structures à poutres.
- A.2 Qu’est-ce qu’un élément fini ?
- Chapitre B. Objectifs de calcul et caractéristiques nécessaires de l’outil
- B. Objectifs du calcul et caractéristiques nécessaires de l’outil
- B.7 Organisation du calcul
- Chapter C. Good practices to create a model
- C.1 Données d’entrée et unités
- C.2 Modélisation des éléments principaux
- C.3 EF et maillage
- C.4 Modélisation des éléments non structuraux ou des équipements
- C.5 Conditions aux limites
- C.6 Connexions – liaisons – assemblage
- C.7 Excentrements
- C.8 Sections composées (poutres/dalles)
- C.9 Matériaux
- C.10 Comportement spécifique au cisaillement et à la torsion
- C.11 Modélisation des charges
- C.12 Compléments liés aux éléments volumiques
- C.13 Compléments liés aux calculs non linéaires
- C.14 Compléments liés au béton précontraint
- C.15 Compléments liés au calcul phasé
- C.16 Compléments liés aux calculs dynamiques et sismiques
- Chapitre D. Analyse et exploitation des résultats
- D.1 Généralités sur les calculs numériques
- D.2 Combinaisons d’actions
- D.3 Exploitation des résultats
- D.4 Validations réglementaires : comportement en béton armé des éléments
- D.5 Comprendre et analyser les pics (cas du béton)
- D.6 Comprendre et analyser les pics (cas d’un assemblage métallique)
- D.7 Compléments spécifiques pour les calculs dynamiques
- Chapitre E. Comment assurer la qualité ?
- E.1 Prise en main d’un nouveau logiciel
- E.2 Validation d’un modèle par autocontrôle
- E.3 Traçabilité et travail à plusieurs
- Chapitre F. Comment bien présenter la note de calcul aux éléments finis ?
- F. Comment bien présenter la note de calcul aux éléments finis ?
- PARTIE 3 - EXEMPLES DE CAS D'ÉTUDE COMPLETS
- EXEMPLES DE CAS D'ÉTUDE COMPLETS
- Exemple A - Immeuble de Grande Hauteur
- Exemple B. Bipoutres mixtes et métalliques
- Exemple C - Modélisation de grillages de poutres
- Exemple D - Cas simple : modélisation d'une roue Br
- Exemple E - Flexion transversale d'un caisson en béton précontraint
- Exemple F - Calculs dynamiques de réservoirs
- Exemple G - Pont à haubans
- BIBLIOGRAPHIE
- SUIVI DES AJOUTS ET MODIFICATIONS
- A3. Choix des éléments finis
Table des matières
EDITORIAL
Le calcul aux éléments finis - un changement de paradigme
Le mot du Conseil Scientifique et Technique
PREAMBULE
Contenu des Recommandations et Conseils - Les auteurs
Laissez-nous vos commentaires et vos contributions pour améliorer le site !
INTRODUCTION
Une petite introduction générale - Analyse structurale et éléments finis
PART 1 – THEORETICAL ELEMENTS
Chapitre A. Généralités
Chapitre B. Dynamique
Chapitre C. Calculs statiques non-linéaires
Chapitre C - Calculs statiques non-linéaires
Chapitre D. Génie civil
Chapitre E. Post-traitements typiques du génie civil
Chapitre E - Post-traitements typiques du génie civil
Chapitre F. Calculs géotechniques
Chapitre F - Calculs géotechniques
PARTIE 2 - ÉLÉMENTS PRATIQUES
Chapitre A. Comprendre les éléments finis
A.1 Que fait le logiciel dans un calcul aux éléments finis ? Exemple des structures à poutres.
A.2 Concrètement qu'est-ce qu'un élément fini ?
Annex 1 – File of the matrix calculation example
Chapitre B. Objectifs de calcul et caractéristiques nécessaires de l’outil
La réalisation d’un modèle de calcul par éléments finis comprend plusieurs étapes. Le choix de l’outil est prépondérant et dépend de plusieurs critères. Une modélisation réussie demande une bonne organisation initiale.
B.1 à B.6 Critères à prendre en compte
Chapitre C. Bonnes pratiques pour monter un modèle
Les différents niveaux d’études et la complexité associée du modèle ont déjà été définis avant l’étape de modélisation dans le contenu du chapitre B. Ce chapitre C présente les simplifications pouvant être adoptées pour créer un modèle structurellement représentatif de la conception de l’ouvrage réel et aux sollicitations qu’il voit.
C.1 Données d'entrée et unités
C.2 Modélisation des éléments principaux
C.3 Éléments finis et maillage
C.4 Modélisation des éléments non structuraux ou équipements
C.6 Connexions - liaisons - assemblages
C.8 Sections composées (poutre/dalle)
C.10 Comportement spécifique au cisaillement et à la torsion
C.12 Compléments liés aux éléments volumiques
C.13 Compléments liés aux calculs non linéaires
C.14 Compléments liés à la précontrainte
C.15 Compléments liés au calcul phasé
C.16 Compléments aux calculs dynamiques et sismiques
Chapitre D. Analyse et exploitation des résultats
D.1 Généralités sur les calculs numériques
D.3 Exploitation des résultats
D.4 Validations réglementaires : comportement en béton armé des éléments
D.5 Comprendre et analyser les pics (cas du béton)
D.6 Comprendre et analyser les pics (cas d’un assemblage métallique)
D.7 Compléments spécifiques pour les calculs dynamiques
Chapitre E. Comment assurer la qualité ?
Nous proposons ci-dessous quelques conseils simples pour déployer une démarche qualité dans les calculs aux éléments finis. Les enjeux principaux sont :
-
La bonne utilisation du logiciel
-
La modélisation appropriée du comportement des structures
-
La traçabilité des hypothèses de modélisation et des résultats.
Les conseils ci-dessous traitent de la bonne prise en main d’un logiciel par un ingénieur ou une équipe, des tests d’autocontrôle que doit impérativement effectuer chaque ingénieur à la fin de sa modélisation, et enfin des éléments minimaux à tracer pour permettre le travail à plusieurs ou la reprise ultérieure d’un modèle.
E.1 Prise en main d’un nouveau logiciel
E.2 Validation d’un modèle par autocontrôle
E.3 Traçabilité et travail à plusieurs
Chapitre F. Comment bien présenter la note de calcul aux éléments finis ?
Le présent paragraphe fournit les éléments minimaux qui doivent figurer dans une note, si l’on veut fournir une description claire d’un modèle de calcul aux éléments finis.
F. Comment bien présenter la note de calcul aux éléments finis ?
PARTIE 3 - EXEMPLES DE CAS D'ÉTUDE COMPLETS
Cette partie contient des exemples de modélisations, pour des objets simples ou plus complexes, sous forme d'études complètes ou partielles, ou encore de comparatifs de modélisations pour une même structure.
Si vous possédez un exemple en stock que vous souhaitez partager (cela peut être une note d'un projet réel rendu anonyme), ou une complexité ou un paradoxe relevé sur un bout de modèle, proposez-nous votre contribution à l'adresse suivante: elements.finis@afgc.asso.fr.
Exemple A - Modélisation d'un immeuble complexe de grande hauteur
Exemple A - Exemple de modélisation d'un immeuble complexe de grande hauteur
Exemple B - Modélisation des ponts mixtes
Exemple B - Modélisation des ponts mixtes et métalliques
Exemple C - Modélisation de grillages de poutres
Exemple C - Modélisation de grillages de poutres
Exemple D - Exemple simple : modélisation d'une roue Br
Exemple D - Modélisation d'une roue Br
Exemple E - Flexion transversale d'un caisson en béton précontraint
Exemple E - Flexion transversale d'un caisson en béton précontraint
Exemple F - Calculs dynamiques de réservoirs
Exemple F - Calculs dynamiques de réservoirs
Exemple G - Pont à haubans
BIBLIOGRAPHIE
SUIVI DES AJOUTS ET MODIFICATIONS
Listes des ajouts et modifications
L'édito AFGC
Thierry Kretz était président du Conseil Scientifique et Technique de l'AFGC au moment du lancement du groupe de travail sur les éléments finis. Il nous livre sa vision de ce travail.
$translationBooksLe calcul aux éléments finis – un changement de paradigme
Le calcul aux éléments finis – un changement de paradigme
Il n’est pas exagéré d’affirmer que le calcul aux éléments finis des structures de génie civil relève d’un changement de paradigme dans le calcul des structures. Il est en effet possible de transposer à l’ingénierie des structures le concept de paradigme défini par Thomas Kuhn dans La structure des révolutions scientifiques : les paradigmes sont des « découvertes scientifiques universellement reconnues, qui pour un temps, fournissent à une communauté de chercheurs des problèmes types et des solutions ».
Malgré son caractère apparemment classique, l’émergence du calcul aux éléments finis est bien une révolution de cette nature. L’ancien monde est celui de la résistance des matériaux classique, basée sur l’hypothèse de Saint Venant et l’hypothèse de Navier-Bernoulli, qui se traduisent dans la théorie des poutres et la théorie des plaques minces. L’ancien monde s’appuie donc sur un ensemble cohérent d’hypothèses et de méthodes de résolution, puis de traduction des résultats en principe de dimensionnement des structures et de leurs renforcements.
Le nouveau monde, celui des éléments finis dans toute leur généralité, se construit sur d’autres bases. Le comportement des matériaux eux-mêmes n’est pas remis en cause, mais les hypothèses de calcul des structures changent. Elles concernent d’une part le maillage, c’est-à-dire le principe et la finesse de discrétisation des structures, d’autre part le choix des types d’éléments, c’est-à-dire les champs de déplacements considérés. Les résultats demandent de nouvelles méthodes d’analyse, pour permettre le dimensionnement sûr des structures et de leur renforcement.
Les règlements de calcul, et en particulier les Eurocodes, sont très largement établis dans la logique des théories classiques d’application de la RDM. Ils proposent des règles simples, largement basées sur l’expérience, et dont le domaine de validité est bien connu. Il s’agit par exemple de l’inclinaison des bielles d’effort tranchant, du dimensionnement des consoles courtes, du contrôle du poinçonnement, etc… Ces règlements autorisent le calcul des structures aux éléments finis, mais restent discrets sur les méthodes de calcul (maillage, choix des éléments) et d’interprétation des résultats. Différentes techniques existent pour traduire les résultats dans des termes compatibles avec les règlements, mais il est certain que « la doctrine du calcul aux éléments finis » est encore en cours d’élaboration.
Le guide de l’AFGC que vous avez entre les mains vise à contribuer à l’établissement de cette nouvelle doctrine. Il reflète la volonté de l’AFGC d’accompagner le développement et l’innovation dans le domaine du Génie Civil, en étant le lieu de partage et de transmission des savoirs et des avancées techniques.
Je remercie le groupe de rédaction et en particulier les deux animateurs, Didier Guth et Claude le Quéré, pour leur travail remarquable et je suis persuadé que ce guide, complété par le site web, restera longtemps un ouvrage de référence pour les ingénieurs des bureaux d’études.
Thierry Kretz - mai 2020
$translationBooks
Préface - Le mot du Conseil Scientifique et Technique
Emmanuel Ferrier est le président du Conseil Scientifique et Technique de l'AFGC. Il nous livre sa préface.
Préface
De nombreux étudiants, ingénieurs, scientifiques et chercheurs utilisent des méthodes numériques, afin de développer ou d’utiliser des programmes informatiques pour résoudre des problèmes d'ingénierie dans le domaine de la construction. Ces méthodes numériques s’appuient sur les calculs aux éléments finis. L’AFGC a souhaité apporter une contribution dans ce domaine et a proposé en 2016 l’ouverture d’un groupe de travail sur les méthodes de calculs aux éléments finis appliquées au secteur de la construction. L’objectif principal de ce groupe de travail est de répondre à un besoin récurrent, fréquemment exprimé : avoir un document pédagogique, à destination, notamment, des jeunes ingénieurs en bureau d’études TP/GC, sur l’exemple des anciens guides du SETRA, traitant de la modélisation aux éléments finis (barres, plaques, coques, …) de structures de génie civil.
L’analyse des éléments finis est un sujet fondamental que tous les ingénieurs des grandes entreprises et bureaux d’ingénierie doivent comprendre pour en faire des outils de conception indispensables.
Ce document fournit un traitement introductif de l’analyse des éléments finis avec un aperçu des différents concepts et applications. Il introduit les concepts de base de la méthode des éléments finis et des exemples d’analyse à l’aide de méthodologies systématiques. Les concepts d’éléments finis impliquant des problèmes unidimensionnels sont discutés en détail afin que le lecteur puisse bien comprendre les concepts et progressivement s’appuyer sur ces problèmes pour l’aider à analyser les problèmes bidimensionnels et tridimensionnels.
Parce que ce domaine est en évolution perpétuelle l’AFGC n’a pas souhaité figer le document sous forme de recommandations comme à son habitude mais a proposé pour la première fois un format numérique qui se veut évolutif dans le temps. Il ne s’agit donc pas de recommandations prénormatives comme pour de nombreux guides de l’AFGC mais d’un document d’aide à la compréhension et de la bonne pratique des éléments finis dans le secteur de la construction.
Le CST de l’AFGC tient à remercier les animateurs du groupe de travail, Claude Le Quéré et Didier Guth, et tous les participants qui par leur travail ont rendus possible la publication de ce document.
Emmanuel Ferrier - mai 2020
Préambule
$translationBooksContenu des Recommandations et Conseils - Les auteurs
Recommendations and Advice Content – The authors
Ce travail collaboratif élaboré par des praticiens confrontés dans leur quotidien à l'utilisation des éléments finis se destine avant tout à un public sortant juste des écoles d'ingénieurs, où souvent seules les bases du calcul EF ont été enseignées, ou en début de carrière. Il vise à répondre à certains questionnements récurrents (par exemple la taille des mailles, comment lisser les pics, …), à éviter certains pièges et à préciser ce que ne font pas les éléments finis. Le Groupe de Travail a préféré adopter la dénomination de Recommandations et Conseils plutôt que Guide pour ce document qui est plus un partage de pratique et une discussion autour des éléments finis qu'un guide exhaustif.
Le contenu de ce site se veut évolutif. Le Groupe de Travail est preneur de toute proposition de correction et de contenu complémentaire, notamment des exemples pour compléter la Partie 3. Pour cela, le lecteur pourra se rendre sur la page des commentaires ou nous écrire à elements.finis@afgc.asso.fr
Les trois parties peuvent être consultées indépendamment.
On trouvera tout d’abord dans la partie 1 les éléments théoriques.
Seront abordés successivement :
-
Le chapitre 1 concerne les généralités sur la méthode ;
-
Le chapitre 2 développe les concepts des calculs aux EF en dynamique ;
-
Le chapitre 3 décrit les calculs statiques non linéaires ;
-
Le chapitre 4 traite de la modélisation des matériaux de génie civil et des questions de prise en compte du phasage ;
-
Le chapitre 5 explicite pourquoi des post-traitements sont nécessaires pour traduire la spécificité du « matériau composé » que constitue le béton armé ;
-
Enfin, le chapitre 6 montrera l’utilisation possible de la méthode des éléments finis dans les problèmes géotechniques La suite du document ne traite plus de ce sujet spécifique.
La partie 2 donne ensuite les éléments à mettre en place dans une étude de structure avec la méthode des éléments finis.
Deux raisons amènent l’ingénieur à procéder par étapes itératives, et en menant différentes étapes de contrôle, et des traitements spécifiques :
-
Tout d’abord, le fait que les méthodes de calcul des éléments finis, découlant des hypothèses de la RDM, et ne sont pas systématiquement compatibles avec les [méthodes de ]calcul règlementaires C’est le cas du béton armé, où le diagramme règlementaire de déformations des sections n’est pas celui représenté par les éléments finis, et où le règlement prévoit des opérations que tous les logiciels ne prennent pas en compte (largeurs participantes, décalage de la courbe des moments lié au fonctionnement en bielles, prise en compte de la fissuration, …), ou encore du métal, où il y a également des écarts entre le calcul réglementaire des assemblages ou des instabilités et les résultats que peuvent donner des calculs éléments finis trop précis ;
-
Ensuite, le fait que le calcul théorique se base sur des éléments homogènes et ne traite pas directement tels que le béton armé. Dans ce cas, des post-traitements sont nécessaires pour traduire le comportement spécifique du béton et de l’armature. Une attention toute particulière doit être apportée aux cartographies de ferraillage (surtout pour les voiles) qui peuvent donner l’illusion que le logiciel fait un calcul règlementaire alors que ce n’est pas toujours le cas ;
La partie 2 donne en préalable des conseils pour entreprendre l’étude d’une structure avec les EF. Ensuite, il présente dans son premier chapitre les objectifs des calculs à mener et dans le second chapitre la modélisation de la structure, en s’attachant à détailler les différents matériaux, le traitement des interfaces, (compléter), dans les différents types de calcul, du plus simple au plus complexe. Le troisième chapitre traite de l’exploitation des résultats. Enfin, les deux derniers chapitres reviennent dans le détail sur les vérifications à mener pour valider les résultats et la présentation finale de la note de calcul qui rendra compte du travail effectué, de la bonne prise en compte des objectifs de service de la construction et des phases intermédiaires de construction, et enfin de sa conformité aux règlements en vigueur.
A toutes les étapes, et en se basant sur des exemples, les auteurs se sont employés à montrer les précautions à prendre dans les simplifications, les contrôles à mener pour s’assurer de la validité des hypothèses et obtenir, comme recherché, une modélisation et des résultats qui traduisent au plus près de la réalité le comportement de la structure étudiée.
Les Auteurs
Ces Recommandations et Conseils ont été rédigées entre 2016 et 2019 dans le cadre du Groupe de Travail sur les Éléments Finis de l'Association Française de Génie Civil (AFGC). Un grand remerciement à tous les contributeurs de ce groupe, rédacteurs et relecteurs. Elles sont publiées en ligne de manière à pouvoir recueillir les remarques, observations, questions des utilisateurs.
Pilotes généraux du guide : C. Le Quéré (Egis) et D. Guth (Setec diadès)
Pilotes de la partie 1 : G. Hervé-Secourgeon (EDF R&D) et P. Bressolette (UCA)
Auteurs principaux des différents chapitres :
-
Chapitre 1 : P. Bressolette (UCA), L. Adelaide (IFSTTAR), L. Jouval (ARTELIA)
-
Chapitre 2 : G. Hervé-Secourgeon (EDF R&D)
-
Chapitre 3 : S. Michel-Ponnelle (EDF R&D)
-
Chapitre 4 : J.-J. Brioist (CEREMA), H. Somja (INSA de Rennes), M. Scalliet (CERIB)
-
Chapitre 5 : G. Hervé-Secourgeon (EDF R&D)
-
Chapitre 6 : Leopoldo Tesser (GDS), S. Burlon (IFSTTAR)
Contributeurs et relecteurs des différents chapitres :
-
Chapitre 1 : G. Hervé-Secourgeon, S. Michel-Ponnelle,J.-J. Brioist, L. Adelaide, J. Waeytens (IFSTTAR)
-
Chapitre 2 : P. Bressolette (UCA), S. Michel-Ponnelle (EDF R&D)
-
Chapitre 3 : J.-J. Brioist (CEREMA), H. Somja (INSA de Rennes)
-
Chapitre 4 : G. Hervé-Secourgeon (EDF R&D), S. Michel-Ponnelle (EDF R&D)
-
Chapitre 5 : P. Bressolette (UCA), Yury Shaparevich (EGIS)
-
Chapitre 6 : E. Bourgeois (IFSTTAR)
Pilotes de la partie 2 : S. Juster (CPA Experts), D. Guth (Setec diadès) et C. Le Quéré (Egis)
Auteurs principaux de cette partie 2 :
-
Arnaud Bouard (SCE)
-
Franck Dubois (VINCI Construction France)
-
Christian Gallois (Areva)
-
Didier Guth (Setec diadès)
-
Landry Jouval (Artelia)
-
Sandrine Juster-Lermitte (CPA Experts)
-
Claude Le Quéré (Egis)
-
Emilie Leroux (Tractebel Engineering)
-
Pascal Mangin (CTICM)
-
Pierre Mazurelle (Arcadis)
-
Jean Michalewicz (ETPO)
-
Gildas Potin (Tractebel Engineering)
-
Vincent Rousseau (Bouygues TPRF)
Relecture de la partie 2 :
-
Valentina Bruno (Setec tpi)
-
Olivier Cheray (A.Aegerter & Dr.O.Bosshardt AG - Ingenieure und Planer)
-
Yavuz Demir (CTE Strasbourg)
-
Franck Dubois (VINCI Construction France)
-
Sylvie Ezran (Setec tpi)
-
Didier Guth (Arcadis)
-
Sébastien Miossec (VINCI Construction France)
* Vous? Nous cherchons des volontaires !
Relecteurs des parties 1 et 2 :
-
Fabien Coulon (VINCI Construction Grands Projets)
-
Thierry Kretz (Ifsttar)
-
Michel Marchetti (Formule Informatique)
-
Stéphane Velin (VINCI Construction Grands Projets)
Pilote de la partie 3 : Christian Gallois (ex-Areva)
Auteurs principaux de la partie 3 :
-
Valentina Bruno (Setec tpi)
-
Jacques Combescure (Artès)
-
Jean-Paul Deveaud (Cerema Centre-Est)
-
Franck Dubois (VINCI Construction France)
-
Sylvie Ezran (Setec tpi)
-
Samy Guezouli (INSA de Rennes)
-
Didier Guth (Setec diadès)
-
Pierre Perrin (Dir Est)
-
Albert Lepeltier (Setec tpi)
-
Aymeric Perret du Cray (Setec tpi)
-
Thierry Richard (VINCI Construction France)
-
Hughes Somja (INSA de Rennes)
-
Benjamin Tritschler (Arcadis)
Laissez nous vos commentaires pour nous permettre d'améliorer le site
Laissez nous vos commentaires pour nous permettre d'améliorer le site
Ce peut être :
-
un point de désaccord ;
-
une proposition d'une meilleure formulation ;
-
une proposition de références bibliographiques ;
-
une proposition de lien vers une page Internet pertinente ;
-
un exemple concret, illustré ou non ;
-
une question.
Merci de laisser vos commentaires sous la forme suivante :
| Date | Nom | Moyen de vous contacter (facultatif) |
| Partie 1 | Chapitre A3.3 | Mon commentaire |
| Partie 2 | Chapitre Ex | Mon commentaire |
| Partie 3 | Exemple y | Mon commentaire |
A vous de jouer
| Date | Nom | Moyen de vous contacter (facultatif) |
| Partie 1 | Chapitre A3.3 | Mon commentaire |
| Partie 2 | Chapitre Ex | Mon commentaire |
| Partie 3 | Exemple y | Mon commentaire |
| Date | Nom | Moyen de vous contacter (facultatif) |
| Partie 1 | Chapitre A3.3 | Mon commentaire |
| Partie 2 | Chapitre Ex | Mon commentaire |
| Partie 3 | Exemple y | Mon commentaire |
ou de nous envoyer un mail à elements.finis@afgc.asso.fr
Introduction
$translationBooksUne petite introduction générale - Analyse structurale et éléments finis
Une petite introduction générale - Analyse structurale et éléments finis
Les projets de construction de génie civil nécessitent de justifier les ouvrages vis-à-vis d’un ensemble de risques identifiés sur la base d’un référentiel technique, s’appuyant en principe sur une règlementation en vigueur ou bien choisie par le maître d’ouvrage. Pour cela les ingénieries procèdent à des études de conception et d’exécution avec des niveaux plus ou moins affinés en fonction de la complexité de l’ouvrage et du stade d’avancement du projet. De plus, en matière de génie civil, il s’agit d’en étudier les aspects structurels, en tenant compte des diverses interactions possibles en fonction de leur prédominance.
Performance structurale
La modélisation et les éléments finis sont des outils au service de l’évaluation de la performance structurale pour la conception et la vérification des projets d’ouvrages de génie civil qui peuvent concerner la construction d’ouvrages neufs, ou encore la réutilisation ou la réhabilitation d’ouvrages existants. Ainsi, la modélisation et les éléments finis répondent avant tout à un besoin, et ne sont pas une fin en soi.
L’appellation « performance structurale » désigne la capacité de la structure à remplir les exigences pour lesquelles elle est conçue, qui se répartissent en trois catégories :
-
la sécurité structurale, qui assure la résistance de la structure aux actions prévues en situation normale ainsi que sa robustesse en situation exceptionnelle ;
-
l’aptitude au service, qui assure le maintien de l’exploitation de la structure ;
-
la durabilité, qui décrit l’aptitude de la structure à demeurer en état d’accomplir ses performances de sécurité structurale et d’aptitude au service dans des conditions données d’utilisation et de maintenance sur une durée de service définie.
L’évaluation de la performance structurale des ouvrages neufs ou existants s’appuie sur la théorie de la fiabilité, et peut se traiter par différentes approches d’évaluation :
-
déterministe (toutes les données sont supposées complétement connues),
-
probabiliste (les données sont entachées d’incertitudes et sont représentées par des variables ou fonctions aléatoires)
-
ou encore semi-probabiliste (reposant sur les notions d’état limite et de coefficients partiels de sécurité).
Analyse structurale
En génie civil, l’évaluation de la performance structurale se traite par une approche semi-probabiliste selon la méthode dite des états limites, comme par exemple proposée par les Eurocodes qui permettent de traiter la plupart des cas d’ouvrages. On parle alors d’analyse structurale, qui est une notion fondamentale des Eurocodes.
L’analyse structurale se fait sur la base d’une modélisation qui résulte d’une réflexion de l’ingénieur et de choix d’hypothèses, en tenant compte des données disponibles (à défaut poser des hypothèses les plus pertinentes possibles, et les vérifier par la suite) : il s’agit en d’autres termes de « bien poser le problème » à résoudre et de définir le système à étudier.
L’analyse structurale est un processus par lequel l’ingénieur établit une représentation simplifiée de la structure mais reproduisant le mieux possible le comportement mécanique de celle-ci.
Modélisation
Selon l’Eurocode, la modélisation structurale doit impliquer des calculs qui doivent être effectués à l'aide de modèles appropriés incluant les variables concernées. Il convient que les modèles structuraux permettent de prédire le comportement structural avec un niveau de précision acceptable. Il convient également que les modèles structuraux soient appropriés aux états-limites considérés, et ce pour chaque étape du projet. Les modèles structuraux utilisés doivent être fondés sur une théorie et une pratique établie, et être vérifiés expérimentalement si besoin est.
La modélisation est donc une démarche, ou encore un processus, qui consiste à concevoir et établir un modèle. Selon ses objectifs et les moyens utilisés, la modélisation peut être menée suivant des approches et des méthodologies distinctes. Il s’agit de représenter un objet ou un phénomène réel extrait de son environnement en le simplifiant par un système isolé suivant un concept ou bien une théorie. Il est construit à partir des phénomènes physiques mis en jeu, et intègre par conséquent les lois de la physique. Cela se traduit par le choix de lois de comportement formulées selon des équations mathématiques adaptées pour chaque matériau et chaque partie d’éléments structurels de l’ouvrage à analyser ; cela conduit donc à résoudre des systèmes d’équations complexes de la mécanique des milieux continus, formulées sous forme d’équations aux dérivées partielles.
La principale spécificité des calculs de génie civil, au regard d’autres domaines de l’ingénierie, tient à la nécessité de prendre en compte des phases de construction, telles que le déblaiement ou le remblaiement, la prise d’un massif de béton, la fixation d’une lierne, la mise en tension ou l’ancrage de câbles. La modélisation traduit ces événements dans le langage de la statique, de différentes façons : par une reprise de calcul avec des contraintes internes (« contraintes initiales »), le changement de raideur de certains éléments (passage d’une raideur nulle à une raideur positive), la disparition ou le changement de nature de certains appuis, des changements de point d’application des chargements, etc.
Les « structures modernes » du génie civil (celles d’après la première révolution industrielle) présentent des caractéristiques favorables à leur calcul : géométrie régulière, motifs répétés, qualité des matériaux de construction (par conformité aux « normes produit »). Elles sont néanmoins affectées par une multitude de facteurs peu ou pas contrôlables : facteurs d’ambiance, comme la nature des terrains sur lesquels elles sont fondées, qualité de leur réalisation, puisque la mise en œuvre des matériaux de construction s’opère parfois dans des conditions d’accès ou dans un contexte météorologique défavorables (sensibilité de certains matériaux comme le bois à l'humidité qui impacte les dimensions et les caractéristiques mécaniques en situations normale (créations de jeux, de frettages…) ou comme l'acier avec la température en situation d'incendie… ), enfin vieillissement hétérogène de leurs différentes parties.
Face au problème du dimensionnement ou de la vérification de l’équilibre des constructions réelles, le calcul des structures repose sur des modélisations, c’est-à-dire des simplifications de constructions réelles : modèles de matériaux, hypothèses cinématiques idéales (liaisons parfaite, bilatérales, indépendantes des réactions), et même sélection arbitraire de ce que l’on fait intervenir dans l’équilibre des constructions (en ne prenant pas en compte certaines parties des édifices, ou en négligeant la participation de certains composants matériels). Ces simplifications impliquent naturellement que les résultats des calculs n’ont qu’un rapport contingent avec les constructions réelles, dans leur environnement. Les résultats d’une modélisation doivent, par conséquent, toujours être examinés avec un regard critique, y compris en remontant aux hypothèses plus ou moins explicites sur lesquelles elle s’est appuyée : avant tout, une isolation du système de son environnement, puis la sélection d'un modèle mathématique et d'une méthode de résolution…
Les solutions exactes étant très rares (limitées à quelques cas d'école), on est amené dans la pratique à procéder à une résolution par utilisation de méthodes approchées :
-
soit de type analytique : par exemple par utilisation de la Résistance des Matériaux (RdM) pour laquelle des considérations géométriques amènent à simplifier la résolution du problème tridimensionnel à un problème bidimensionnel (feuillet moyen des plaques et coques) ou monodimensionnel (fibre moyenne des poutres) …
-
soit de type numérique : méthode des éléments finis (MEF), différences finies …
Afin de valider les résultats obtenus, une comparaison avec des mesures expérimentales peut être réalisée. Il est important de souligner que différentes sources d’erreur sont présentes dans cette comparaison. On peut notamment distinguer :
-
l’erreur de modèle, provenant de la simplification du problème réel par un modèle simplifié,
-
l’erreur de discrétisation, due à la résolution numérique du problème,
-
l'erreur de mesure, liée à l'instrumentation et à la prise de mesure,
les résultats obtenus étant, dans le cas idéal, à comparer aux mesures expérimentales, pouvant être elles-mêmes entachées d'erreurs… Il est de plus possible de combiner les deux familles de méthodes approchées : MEF en théorie des poutres, différences finies en théorie des plaques…
La simplification doit permettre de résoudre le problème afin d’évaluer numériquement les effets (efforts, contraintes, déplacements) des différentes sollicitations vues par la structure. Elle doit néanmoins coller le mieux possible avec la structure réelle.

Du problème à sa résolution approchée
Méthode aux éléments finis
La méthode aux éléments finis (MEF) est avant tout un outil de modélisation, qui permet la résolution numérique approchée des problèmes posés à base d’équations aux dérivées partielles. La méthode des éléments finis est applicable aux ouvrages de génie civil, dans la mesure où les matériaux des constructions modernes, comme l’acier ou le béton, permettent l’hypothèse de matière continue, hypothèse structurante pour la formulation des éléments finis. Cela suppose qu’avant son emploi, l’ingénieur a procédé à une première réflexion sur son utilisation dans ses études, et qu’il est conscient de la démarche de modélisation.
La MEF est une méthode numérique générale permettant de traiter des problèmes réels (« industriels ») de différents domaines (mécanique des solides, des fluides, thermique…) sur des milieux continus, en statique ou dynamique, linéaire ou non-linéaire, ainsi que des problèmes couplés : thermo-mécanique (structure en situation d'incendie), fluide-structure (vibrations d'un réservoir contenant un liquide), chimie-mécanique (prise en compte de la corrosion des armatures dans le béton armé) … Son essor est lié à celui de l'informatique depuis les années 1980 et a donné lieu à la création d'un grand nombre de logiciels. Ce guide ne traite que de l’utilisation des éléments finis, mais cette méthode n’est naturellement pas la seule technique en calcul de structure : outre certaines approches traditionnelles comme la statique graphique, l’emploi d’abaques ou les techniques analogiques sur maquettes (reconnues par les Eurocodes structuraux), on dispose aujourd’hui de bien d’autres outils (méthodes spectrales, éléments de frontière (BEM), éléments discrets, etc.), certains encore proches de la recherche, mais la MEF est la plus générale et la plus utilisée dans la pratique, ayant eu un grand essor lié à l’essor de l’informatique depuis les années 1980 et donné lieu à la création d’un grand nombre de logiciels.
D'une manière très globale, le principe général de la MEF peut être résumé de la façon suivante : le domaine d'étude, de forme a priori complexe, est découpé (discrétisé) en un grand nombre de sous-domaines de formes simples (les éléments finis) sur lesquels sont distingués des points (les nœuds) : on définit de la sorte un maillage. La solution approchée du problème n’est calculée qu’aux nœuds (solution discrète), la solution approchée continue sur le domaine étant obtenue en tout point par interpolation des valeurs aux nœuds.
Plus précisément, les différentes étapes de la MEF sont :
-
Discrétisation de la structure en un ensemble de nœuds reliés par des éléments de comportement connu. Établissement du vecteur colonne déplacement D, regroupant les N degrés de libertés de la structure. Les degrés de liberté sont les déplacements (translations et rotations, selon le type de modélisation) possibles de la structure. Ce sont les inconnus du problème, qui se traite donc dans l’espace RN
-
Établissement du comportement des éléments. Ce comportement comporte deux parties :
-
La détermination des forces de déplacement fed : ce sont les forces exercées par les nœuds reliés à l’élément sur cet élément, pour lui imposer leur déplacement de. La relation est établie dans un repère local propre à l’élément, puis transposée dans l’espace des degrés de liberté : FeD = Ke.De. On peut reprendre ici la relation donnée en 1 p 8, mais dans un but didactique, il peut être préférable de traiter séparément la question du comportement unitaire des éléments (qui relève d’une sorte de bibliothèque comportementale dans laquelle on vient piocher)
-
La détermination des forces de blocage feb : ce sont les forces exercées par les nœuds sur un élément directement chargé, pour l’empêcher de bouger ; les noeuds jouent ici un rôle virtuel d’appui pour l’élément, et on détermine les réactions d’appui, d’abord dans un repère local de l’élement, feb, puis dans l’espace des degrés de liberté : FeB
-
-
Assemblage. Établissement de la matrice de rigidité de la structure et des forces exercées par les noeuds sur les éléments en raison de leur chargement. Ceci se fait par addition, dans l’espace RN pour les vecteurs et RN x RN pour les matrices, des matrices de rigidité élémentaires et des forces de blocage : K = ∑ Ke et FB = ∑ FBe
-
Écriture et résolution de l’équation en déplacements, qui est en fait l’équation d’équilibre des nœuds. Les nœuds exercent sur les éléments des forces pour leur imposer un déplacement D (KD) et des forces de blocage en réaction des charges directement appliquées sur les éléments (FB). Les nœuds peuvent être soumis à des forces extérieures qui seraient directement appliquées aux nœuds (FN), comme les réactions d’appui par exemple. L’équation général s’écrit : KD = F (avec F = FN – FB)
-
Résolution : calcul des déplacements : D = K-1F. On pratique, on doit distinguer les degrés de liberté dont les valeurs sont connues (les appuis) des autres. On note D1 les degrés de liberté inconnus et D2 les degrés de liberté connus et on organise l’espace des degrés de liberté en mettant d’abord ceux qui sont inconnus. L’équation générique s’écrit alors
 . Dans cette équation, F1 et D2 sont connus. On détermine donc
. Dans cette équation, F1 et D2 sont connus. On détermine donc  puis F2.
puis F2. -
Connaissant les déplacements, on peut déterminer les efforts sur les éléments en revenant sur les équations de comportement élémentaire de chaque élément.

Géométrie et maillage (éléments finis triangulaires et nœuds)
Le présent guide s’attache à décrire les outils disponibles couramment dans les programmes de calcul de structures par éléments finis, en statique et en dynamique. Pour des raisons de place et de clarté, nous avons choisi de laisser de côté les problèmes d’écoulements interstitiels, malgré leur grand intérêt en géotechnique ; du point de vue des difficultés de modélisation, ce champ d’application, couvert lui aussi par la méthode des éléments finis, pose des problèmes tantôt analogues à ceux que l’on rencontre en dynamique des structures (choix du pas de temps), tantôt en élastoplasticité (contrastes de perméabilité, frontière entre zone saturée et non-saturée, etc.).
La méthode des éléments finis est un outil numérique de résolution numérique. La modélisation qui précède cette résolution peut s’appuyer sur l’ensemble des principes de l’analyse structurale qui préexistaient.
PARTIE 1 - ÉLÉMENTS THÉORIQUES
$translationBooksChapitre A. Généralités
Chapitre A. Généralités
Lors du calcul d’une structure par éléments finis, le cadre des hypothèses de modélisation doit être posé ainsi que les objectifs à atteindre, qui sont généralement la détermination de :
-
la configuration déformée provoquée par un chargement statique (permanent), quasi statique (sans effet d’inertie) ou dynamique (chargement rapide) ;
-
l’état interne tel que les contraintes, les dommages induits (fissuration, etc.).
Parmi les hypothèses de modélisation, il est préférable de traiter, par ordre chronologique :
-
le choix de la formulation générale ;
-
la dimensionnalité de la modélisation ;
-
le choix des éléments ;
-
la définition des interactions avec l’environnement.
A1. Formulation générale pour les calculs élastiques linéaires
A1. Formulation générale pour les calculs élastiques linéaires
A2. Dimensionnalité de la modélisation
A2. Dimensionnalité de la modélisation
A3. Choix des éléments finis
A4. Interaction entre la structure et son environnement
A4. Interaction entre la structure et son environnement
A5. Estimation de la qualité de la solution numérique approchée
A5. Estimation de la qualité de la solution numérique approchée
$translationBooksA1. Formulation générale pour les calculs élastiques linéaires
A1. Formulation générale pour les calculs élastiques linéaires
La formulation qui n’est plus réellement à faire car la majorité des logiciels proposés de nos jours s’appuie sur une formulation en déplacement car la prise en compte des conditions aux limites ne pose pas de difficulté notoire à l’inverse d’une formulation en contrainte. Il existe également la formulation mixte en déplacement et en contrainte. Ces trois formulations sont les principales, mais il existe d’autres formulations que nous n’évoquerons pas dans ce chapitre.
Dans ce document, nous ne présentons que la formulation en déplacement (la plus utilisée) : dans ce cadre, les inconnues de base sont les déplacements aux nœuds, notés classiquement q, dont sont déduits tous les autres résultats (déformations ε, contraintes σ …).
Les déplacements en tout point d'un élément, notés u(x,y,z), sont obtenus par interpolation des valeurs aux nœuds, à l'aide des fonctions d'interpolation (appelées fonction de forme), notées N(x,y,z), polynomiales de degré faible (1 à 3 en général) :

La relation déformations - déplacements s'obtient par dérivation à l'aide de l'opérateur (matrice) de dérivation D (différent selon le contexte), faisant apparaître la matrice B reliant déformations et déplacements aux nœuds :

Pour obtenir les contraintes, il est enfin indispensable d'introduire la loi de comportement du matériau constitutif. Ainsi, en élasticité linéaire, la relation contrainte – déformation s'écrit (avec H la matrice de Hooke) :

On constate donc que toutes les quantités d'intérêt (déplacements en tout point, déformations, contraintes) s'obtiennent à partir de la connaissance des déplacements aux nœuds du maillage
Remarque : comme les déformations (et donc les contraintes) sont obtenues par dérivation des déplacements aux nœuds, il y a dégradation de la précision lors du calcul de ces grandeurs.
Pour un calcul statique en mécanique des structures, la détermination de la solution numérique du problème par la Méthode des Éléments Finis (MEF) peut se résumer en 4 étapes principales :
Étape 1. Détermination des matrices et des vecteurs élémentaires sur chaque élément de volume V par les relations suivantes (la notation BT désignant la transposée de la matrice B) :
 matrice élémentaire de rigidité
matrice élémentaire de rigidité
 vecteur élémentaire des charges équivalentes
vecteur élémentaire des charges équivalentes
avec  le vecteur des charges volumiques et
le vecteur des charges volumiques et  celui des charges surfaciques. Le vecteur des charges équivalentes permet de « ramener aux nœuds » les charges appliquées aux éléments (dans le volume ou en surface), selon l'interpolation retenue
celui des charges surfaciques. Le vecteur des charges équivalentes permet de « ramener aux nœuds » les charges appliquées aux éléments (dans le volume ou en surface), selon l'interpolation retenue
Attention, cela ne correspond en général pas à l'équirépartition aux nœuds de la charge totale appliquée à un élément.
Étape 2. Calcul de la matrice de rigidité K et du vecteur des charges F à l’échelle de la structure par assemblage des quantités élémentaires et introduction des conditions aux limites.
Étape 3. Détermination du vecteur q des déplacements nodaux par la résolution du système linéaire (de grande taille) :

Le vecteur q donne la valeur du déplacement aux nœuds du maillage, comme c'est le cas du vecteur des charges équivalentes F.
Etape 4. Déduction des quantités d’intérêt telles que déformations et contraintes par un post-traitement du vecteur q des déplacements nodaux.
En revenant au niveau des éléments, les valeurs des déplacements en tout point, des déformations et des contraintes sont déduites des déplacements aux nœuds à l'aide des relations précédentes. Contrairement aux déplacements, les contraintes et les déformations sont des grandeurs calculées élément par élément (et il n'y a pas toujours continuité de ces quantités d'un élément à l'autre).
Remarque : il est possible de faire une analogie entre résolution par éléments finis d'un problème mécanique et d'un problème thermique en régime permanent linéaire : dans ce cas, les températures aux nœuds T sont obtenues en résolvant le système linéaire : Λ.T = Φ, Λ étant la matrice de conductivité et Φ le vecteur des flux aux nœuds.
Le degré des fonctions de forme N(x,y,z), qui se déduit pour les éléments massifs (ou de mécanique des milieux continus - MMC) du nombre de nœuds sur l'arête d'un élément fini (2 nœuds : éléments linéaires, 3 nœuds : éléments quadratiques) se répercute sur le degré des déformations et des contraintes évaluées par éléments finis. Par exemple, si l'opérateur de dérivation D correspond à des dérivées premières (cas de la MMC), les déformations et contraintes seront constantes par éléments pour des éléments linéaires, linéaires pour des éléments quadratiques… Pour mémoire, en RdM, les déformations font intervenir des dérivées d'ordre 2 (flexion des poutres, plaques…).

Fonctions de forme - Triangle à 3 noeuds (fonctions linéaires)

Fonctions de forme - Triangle à 6 noeuds (fonctions quadratiques)
Attention : il n'est pas possible de mélanger dans un même maillage des éléments finis dont les fonctions de forme sont de degrés différents (par exemple éléments linéaires et quadratiques). En effet, la continuité des déplacements ne peut être assurée à l'interface d'éléments de fonctions de forme de degrés différents.
Dans les logiciels, la plupart des éléments finis sont dits isoparamétriques, c'est-à-dire que les différents éléments finis d'un maillage sont construits par transformation géométrique d'un élément de référence (lui-même exprimé dans un repère de coordonnées unitaires ξ,η,χ).

Élément isoparamétrique (quadratique) : différentes transformations (2D)
Ces transformations géométriques, reposant en général sur les mêmes nœuds que l'interpolation sur les déplacements (d'où le qualificatif « isoparamétrique » : mêmes paramètres), sont en particulier caractérisées par leur matrice jacobienne J (matrice des dérivées partielles du premier ordre de la transformation géométrique).

Élément isoparamétrique (quadratique) : repère local et global (2D)
Un des avantages de cette transformation est la possibilité d'approcher les frontières du domaine d'étude par des géométries polynomiales. Cependant, l'inconvénient principal est de complexifier le calcul des matrices et vecteurs élémentaires. Leur évaluation se fait alors par intégration numérique à l'aide d'un schéma de type quadrature : somme pondérée de valeurs en certains points situés à l'intérieur des éléments (poids ω_i, points ξ_i) caractéristiques de la méthode (méthode de Gauss, de Hammer…). Dans ce cas, le calcul de la matrice de rigidité élémentaire et du vecteur élémentaire des charges équivalentes (aux charges volumiques) s'écrivent :




Quand les matrices (faisant intervenir la matrice B) sont évaluées de cette façon, il est naturel de calculer aux mêmes points les contraintes et les déformations (également fonction de B). Les logiciels fournissent alors ces grandeurs aux points d’intégration (aux points de Gauss ou de Hammer selon le schéma d'intégration) ; de plus, parler de valeurs aux nœuds d'un maillage pour les contraintes ou les déformations n'a pas de sens, car il y a autant de valeurs en un nœud qu'il y a d'éléments concourants en ce point et il n'y a pas forcément continuité d'un élément à l'autre ! Vouloir à tout prix obtenir une valeur (de contrainte ou de déformation) en un nœud du maillage suppose donc un traitement : extrapolation à partir des valeurs aux points d'intégration et moyenne des valeurs provenant des différents éléments concourants, qui conduit au minimum à un lissage des résultats obtenus (cependant, parler de valeur aux nœuds d'un élément particulier est justifié). Quand ces quantités sont obtenues par intégration analytique (cas des poutres par exemples), elles peuvent être exprimées aux nœuds, au centre de gravité… les remarques précédentes sur la continuité entre éléments restant valables.
Remarque : certains éléments finis présents dans les codes sont dits sous-intégrés (ou à intégration réduite) : il s'agit d'éléments pour lesquels l'intégration numérique lors du calcul des quantités élémentaires (matrice de rigidité et vecteur des charges équivalentes) est effectuée avec moins de points que celui mathématiquement nécessaire ; cela peut améliorer dans certains cas la précision des calculs (en évitant les phénomènes de bloquage mais également conduire à des problèmes numériques (matrice singulière par exemple ou apparition de modes d’hourglass).

Éléments quadratiques et points d'intégration (points de Gauss)
La façon de prendre en compte les conditions aux limites en déplacement (encastrement, appuis…) peut entraîner des différences de résultats selon la technique numérique retenue, qui peuvent être résumées à deux : la méthode de pénalisation, simple à mettre en œuvre mais qui présente l'inconvénient d'être sensible à l'ordre de grandeur des termes de la matrice de rigidité et la méthode des multiplicateurs de Lagrange, insensible aux problèmes de précision évoqués pour la première mais augmentant légèrement la taille du système à résoudre.

la matrice de masse étant obtenue par assemblage des matrices de masse élémentaires  (masse volumique) et C étant la matrice d'amortissement (visqueux). Ceci nécessite la résolution d'un système d'équations différentielles par des méthodes numériques adéquates (cf. chapitre dynamique).
(masse volumique) et C étant la matrice d'amortissement (visqueux). Ceci nécessite la résolution d'un système d'équations différentielles par des méthodes numériques adéquates (cf. chapitre dynamique).
A2. Dimensionalité de la modélisation
A2. Dimensionnalité de la modélisation
Il est indispensable de transformer le problème réel autrement dit de le simplifier pour modéliser l’interaction entre la structure et son environnement. Pour ce faire, il existe 2 techniques :
-
La première est de passer d’un problème spatial à un problème de dimension réduite tel que l’axisymétrie ou le 2D plan (en contraintes planes ou en déformations planes). Elle permet une réduction de l’espace (cf. §2.2).
-
La seconde permet de rester dans la dimension 3D mais en tenant compte d’une réduction du modèle grâce à des hypothèses cinématiques. Ceci est constaté lors du passage à la théorie des poutres, des plaques ou des coques (cf. §2.1).
Ces 2 techniques induisent des coûts de calcul réduits. En revanche, l’utilisateur doit faire très attention à la simplification employée car cette dernière fait appel à des hypothèses qui doivent rester dans le domaine de validité du problème réel afin d’obtenir des résultats pertinents.
1) Cas des éléments finis de RDM
Du point de vue des éléments finis, la différence essentielle entre MMC et RdM concerne la géométrie qui est simplifiée moyennant des hypothèses supplémentaires : le problème tridimensionnel initial est alors ramené à un problème bidimensionnel (surface moyenne pour les plaques et coques) ou unidimensionnel (fibre moyenne pour les barres et poutres), mais représenté dans un espace tridimensionnel (à la différence des problèmes plan, cf. ci-dessous). Lorsque la MEF est utilisée pour résoudre un problème de RdM, les éléments finis sont donc des éléments spécifiques, pour lesquels il faudra fournir des caractéristiques géométriques (section, inerties pour les poutres, épaisseur pour les plaques et coques). De plus, ils combinent les effets de traction/compression (pour les poutres), ou de membrane (pour les plaques et coques), qui sont traités de manière similaire à la MMC, aux effets de flexion, qui sont traités spécifiquement.
Pour la partie flexion, la simplification géométrique induit une définition particulière des déformations, ce qui entraîne pratiquement des expressions différentes de l'opérateur de dérivation D selon les cas. Une autre conséquence porte sur la définition des inconnues aux nœuds : en effet, alors qu'en MMC, les inconnues sont les composantes du déplacement, en RdM, on est amené à rajouter des inconnues correspondant aux rotations, puisqu'il n'est plus possible de les évaluer directement à partir des déplacements aux nœuds en raison de la simplification géométrique. Le choix initial de traiter le problème posé en MMC ou RdM implique donc le choix d'éléments finis dans des familles différentes ; il est de plus a priori interdit de les mélanger car, à l'interface entre éléments de natures différentes, on se retrouve avec des rotations non transmises, sauf disposition spécifique. De plus, les contraintes calculées sur ces éléments sont en général des contraintes généralisées (ou efforts de la RdM : effort normal, tranchant, moment de torsion, fléchissant). Pour obtenir les contraintes (de la MMC) en un point, il est nécessaire de fournir des informations supplémentaires (position dans la section de la poutre par exemple).
Dans ce cadre, le choix d'un élément fini présente une difficulté supplémentaire liée à la prise en compte ou pas de l'énergie de cisaillement (éléments de poutre de Euler-Bernoulli ou de Timoschenko, éléments de plaque de Love-Kirchoff ou de Reissner-Mindlin), ce choix étant lié à des considérations géométriques (élancement de la section de la poutre ou épaisseur de la plaque). De plus, dans le cas où on choisit de prendre en compte l'énergie de cisaillement, des problèmes numériques peuvent intervenir (blocage en cisaillement), qui rendent certains éléments finis d'utilisation délicate
L'élément fini de poutre d'Euler-Bernoulli permet de représenter exactement un moment fléchissant variant linéairement le long de la fibre moyenne d'un élément (les fonctions de forme étant de degré 3 pour les déplacements de flexion et le moment obtenu par dérivée seconde des déplacements) : il n'est donc pas utile de mettre plusieurs éléments entre nœuds chargés par des forces ponctuelles (alors qu'il faut mailler finement lorsque le chargement est réparti entre 2 points).
Enfin, pour les éléments de plaque et coque, la convergence monotone n'est pas toujours assurée selon la forme du maillage, ce comportement étant lié à la formulation même des éléments. Ce type de comportement est illustré sur la figure ci-dessous, montrant l'évolution de l'erreur relative sur la flèche ω et le moment Mx en fonction du logarithme du nombre de degrés de liberté (dans le cas d'une plaque rectangulaire appuyée sur ses quatre côtés soumise à une charge uniforme) : en vert, un élément non-conforme (COQ3) dont les résultats sont bien moins précis qu'un élément conforme (DKT), et de plus dont la convergence n'est pas monotone (pour les moments Mx sur la figure) : plus d'éléments conduit paradoxalement à un résultat qui peut être moins précis !


Plaque en flexion : convergence (flèche ω et moment Mx) en fonction du log du nombre de degrés de liberté
Ce domaine, particulièrement important en génie civil, présente donc des difficultés spécifiques qui seront développées dans les prochains chapitres.
2) Calculs bidimensionnels
Les problèmes étudiés sont par nature tridimensionnels ; cependant, il est plus rapide d'effectuer des calculs bidimensionnels. Dans certains cas, il est possible de ramener l'étude d'un problème tridimensionnel à celui d'un problème bidimensionnel :
-
si le problème admet un axe de révolution (pour la géométrie, le chargement et les conditions aux limites) : il est possible de faire un calcul axisymétrique pour lequel aucune hypothèse supplémentaire n'est faite ; dans le cas où le chargement n'est pas axisymétrique, il est possible de le décomposer en séries de Fourier et de traiter le problème initial par superposition de calculs axisymétrique ;

Cylindre sous pression ➡ axisymétrie
-
si on fait l'hypothèse de négliger les contraintes ou les déformations hors plan selon que la structure a une épaisseur très faibles ou très importante : on se place donc en hypothèse de contraintes planes ou de déformations planes respectivement ; la solution obtenue est alors une approximation du problème tridimensionnel. Il faut garder en tête qu'en contraintes planes, les déformations hors plan sont non nulles (idem en déformations planes pour les contraintes hors plan).
 Barrage : épaisseur importante ➡ déformations planes
Barrage : épaisseur importante ➡ déformations planes
 Assemblage : faible épaisseur ➡ contraintes planes
Assemblage : faible épaisseur ➡ contraintes planes
3) Prise en compte de symétries
Certains problèmes présentent des symétries (axe de symétrie, plan de symétrie…) et il peut être intéressant d'en profiter pour rendre les calculs par éléments finis plus rapides. Il faut cependant se souvenir que la résolution ne fournira que des solutions elles-mêmes symétriques (notamment lors de calculs de modes propres).
Pour cela, il est important d'avoir en tête que, comme mentionné ci-dessus, la symétrie doit concerner aussi bien la géométrie, que le chargement et les conditions aux limites pour pouvoir être prise en compte dans le calcul. La solution de la partie de la structure modélisée ne représentera cependant la solution du problème complet que si les conditions de symétrie sont intégrées au modèle. En mécanique des solides (MMC), celles-ci consistent à imposer que les composantes du déplacement perpendiculaires à l'axe/au plan de symétrie sont nulles. En RdM, il convient de penser à ajouter la condition de nullité des rotations autour de l'axe perpendiculaire à l'axe/au plan de symétrie. Enfin, la prise en compte de la symétrie peut avoir des conséquences sur le chargement : par exemple, il faut penser à n'appliquer que la moitié de l'intensité d'une charge ponctuelle appliquée sur un axe de symétrie.
$translationBooksA3. Choix des éléments finis
A3. Choix des éléments finis
Le choix de l’élément est une étape importante. L’objectif est de sélectionner le type d’élément (à savoir sa forme et l’ordre des fonctions de forme associées) et la taille de l’élément. Le type et la taille des éléments définissent l’allure et la précision des champs de déplacement, donc, de déformation et de contraintes.
En plus, de la forme de l’élément, vient s’ajouter son aspect. Il faut éviter de produire des éléments dégénérés ou trop dénaturés (aplatis ou allongés) car cela dégrade la précision de la résolution du problème.
De manière plus globale, le maillage généré peut être structuré (répartition régulière des éléments) ou non structuré. Il est possible de combiner sur un même domaine des parties structurées et non structurées suivant la complexité géométrique.
Dans le même esprit, la taille de l’élément choisi est dépendante de la géométrie de la structure à mailler et des chargements qui lui sont appliqués. Les zones à fortes variations (gradients) de contrainte ou à contraintes élevées (contact-frottant ou fissuration par exemple) déterminent les parties nécessitant une finesse de maillage supérieure aux autres parties pour bien percevoir les contraintes ainsi que les déformations.
Une des premières règles à respecter est de lancer une première simulation avec un premier maillage afin de déterminer les zones sensibles énumérées précédemment et ensuite raffiner le maillage où cela s’avère nécessaire.
Le modélisateur doit avoir un regard critique sur son maillage vis-à-vis de la géométrie de la structure et des zones importantes à observer.
Pour bien choisir les éléments finis à utiliser lors du maillage, il est nécessaire de réfléchir au type de calcul souhaité :
-
l'ensemble de la géométrie va-t-elle être représentée, auquel cas le problème relève de la MMC et les éléments sont donc de type « massif » ; dans ce cas, il faut savoir si le problème est tridimensionnel ou bidimensionnel (contraintes planes, déformations planes, axisymétrie… cf. 3.) et si on souhaite utiliser des éléments finis à fonctions de forme linéaires ou quadratiques : la précision des calculs est meilleure avec un maillage d'éléments quadratiques mais a un coût de calcul plus important : il faut donc faire un compromis ; dans tous les cas, les degrés de liberté sont les composantes du déplacement (u, v en 2D, u, v, w en 3D) ; les principaux éléments sont listés dans le tableau ci-dessous ;

-
ou la géométrie est simplifiée, cas de la RdM (ou calcul des structures cf. 2.) : dans ce dernier cas, les éléments finis sont donc
-
des éléments de barre/poutre (une barre ne reprend que de la traction ou de la compression à la différence d'une poutre qui reprend en plus de la flexion ; attention, certains logiciels ne différencient pas les deux et parlent d'éléments de barre pour désigner également des éléments de poutre)
-
des éléments de plaque/coque (la différence entre plaque et coque est liée à la courbure du feuillet moyen et la plupart des logiciels ne font pas la distinction).
-
Pour ces éléments, en plus des degrés de liberté de déplacement, les éléments de RdM comportent des degrés de liberté de rotation (θx, θy, θz), permettant de prendre en compte la géométrie non maillée (section pour les poutres, épaisseur pour les plaques et coques). De plus, se pose la question de savoir si l'énergie de cisaillement doit être prise en compte ou pas (éléments de poutre de Navier-Bernoulli ou de Timoshenko, éléments de coque de Love-Kirchhoff ou de Mindlin-Reissner). Dans le cas des éléments de coque, comme mentionné auparavant, se pose enfin la question de la qualité des éléments (éléments conformes ou pas). Il est donc particulièrement difficile de faire le choix d'un élément fini de plaque/coque, en particulier lorsque la documentation est succincte ; il peut être judicieux dans ce cas, de réaliser un calcul sur un cas dont la solution est connue afin de tester la qualité des éléments disponibles.
En RdM, les différents éléments généralement rencontrés sont décrits dans le tableau II ci-dessous.

A.4. Interaction entre la structure et son environnement
A.4. Interaction entre la structure et son environnement
La prise en compte de l’interaction entre la structure et son environnement : cette considération permet de diminuer au mieux les écarts entre la modélisation par éléments finis et la réalité. L’effet de l’environnement sur la structure est déterminé à partir de grandeurs nodales telles que les déplacements nodaux et les efforts nodaux. Les premiers sont liés aux conditions aux limites et les seconds aux chargements extérieurs [1].
-
Les conditions aux limites en déplacement (nodaux) permettent d’imposer aux nœuds une valeur de leur déplacement (nulle ou non nulle). Les déplacements imposés sont souvent appelés contraintes cinématiques. Elles permettent également de lier les déplacements de certains nœuds. Dans un premier temps, il est préférable de déterminer s’il faut prendre en compte la ou les symétries avant d’imposer les conditions aux limites. L’utilisation de symétrie impose de bloquer les déplacements nodaux perpendiculaires au plan de symétrie en 3D ou à l’axe de symétrie en 2D en imposant une valeur nulle (Figure 3) (cf. §4).

Conditions aux limites correspondant à une symétrie par rapport à deux axes dans le cas de la plaque trouée sollicitée en traction
Dans un 2ème temps, il est indispensable de neutraliser les mouvements de corps rigide. Une modélisation par éléments finis correctement définie doit interdire les translations et les rotations libres. En 3D, il faut donc éviter les 6 mouvements de corps rigide énoncés précédemment (en 2D, il s’agit de 3 mouvements, Figure 4).

Mouvements de corps possibles en 2D : a) Translation horizontale possible ; b) Translation verticale possible ; c) Rotation autour de la rotule ; d) Tout mouvement de corps rigide neutralisé
Une fois ces deux étapes réalisées, il est nécessaire de vérifier que tous les mouvements de corps rigide sont correctement annulés et qu’aucun mouvement de corps rigide n’a été bloqué alors que ce mode avait déjà été supprimé. Dans le premier cas, aucun calcul n’est possible et dans le second cas, des déformations non attendues risquent d’apparaître.
-
Le chargement correspond à des efforts extérieurs exercés sur certaines parties du maillage. Parmi les chargements, il existe les forces à distance telles que la pesanteur et les inerties. Elles sont généralement modélisées par des forces volumiques traduites par des forces nodales sur l’ensemble des nœuds du domaine. Ce type de force est souvent simple à mettre en place.
Il existe également les forces de contact telles que les pressions ou toute autre force nécessitant un contact avec la structure. Ces forces peuvent être surfaciques, linéiques ou ponctuelles. L’application de ces forces se traduit également par des forces nodales. Une attention particulière doit être portée à la traduction de ces forces de contact lors de la modélisation vis-à-vis de son domaine de validité. L’utilisation d’une force ponctuelle peut gérer des singularités telles qu’une concentration de contraintes dans le voisinage proche du nœud d’application de la force ponctuelle. Donc pour éviter ce type de singularité, il est nécessaire de répartir la charge par l’intermédiaire d’un patin sur lequel la force ponctuelle sera appliquée. Cela revient à appliquer une force surfacique sur la structure englobant un voisinage plus ou moins grand du point d’application de la force ponctuelle. Se pose alors la question du raffinement de maillage dans cette zone et son influence que les résultats obtenus.
Les conditions de raccords
Il existe différents types d’éléments finis tels que les éléments volumiques, plaques, coques, poutres et barres. Les plaques et coques minces sont des éléments dont l’épaisseur est plus petite que les 2 autres dimensions. Une plaque ne travaille que perpendiculairement à son plan (3 degrés de liberté (ddl) par nœud : une translation et 2 rotations) alors qu’une coque travaille dans son plan et perpendiculairement à celui-ci (6 ddl : 3 translations et 3 rotations). Les éléments volumiques ont 6 ddl par nœud. Les éléments poutres ont 6 ddl par nœud également en 3D. Le chapitre 2 présente des développements pratiques sur ce point.
$translationBooksA.5. Estimation de la qualité de la solution numérique approchée
A.5. Estimation de la qualité de la solution numérique approchée
L’écart entre la solution exacte du problème et la solution approchée obtenue par la méthode des éléments finis permet de connaître la qualité de la solution : c'est l'« erreur de discrétisation ». La solution exacte n’étant généralement pas connue, l’idée consiste à estimer cet écart en calculant un « estimateur d’erreur ». On distingue :
-
des estimateurs d’erreur globale afin d’évaluer la qualité de la solution sur l’ensemble du domaine (méthode de lissage des contraintes, des résidus d'équilibre, de l'erreur en relation de comportement…),
-
des estimateurs d’erreur locale afin d’évaluer la qualité d’une quantité d’intérêt telle que le déplacement en un point ou la contrainte dans une zone (méthode des résidus d'équilibre pondérés…).
Ces différents outils d’estimateur d’erreur, disponibles selon les logiciels utilisés, pour un coût numérique variable, peuvent être utilisés dans deux buts :
-
améliorer la qualité des résultats d’un calcul par éléments finis en raffinant de façon automatique le maillage et/ou la discrétisation temporelle,
-
obtenir un intervalle de confiance (bornes inférieure et supérieure) associée au calcul de l’erreur globale ou sur une quantité d’intérêt.
Il est important de souligner que certains estimateurs d’erreur, tels que les méthodes de lissage des contraintes, permettent uniquement d’avoir une indication de l’erreur commise alors que d'autres, tels que les méthodes des résidus d’équilibre, permettent de garantir les résultats numériques obtenus via le calcul d’un encadrement de l’erreur.
$translationBooksChapitre B. Dynamique
Chapitre B. Dynamique
Pour un certain nombre d’applications, tel que les calculs sismiques, les impacts, les études vibratoires, … il est nécessaire de considérer les phénomènes dynamiques.
Les chargements dynamiques appliqués à une structure de génie civil appartiennent basiquement à deux catégories :
-
les phénomènes assimilables à des phénomènes stationnaires : écoulement permanent de vent, houle, machine tournante,
-
les phénomènes transitoires : impact, explosion, séisme.
Concernant les mouvements sismiques, s’ils sont théoriquement considérés comme transitoire, il est néanmoins admis de les assimiler comme des phénomènes stationnaires pendant leur durée de phase forte. Pour les cas où l'on cherche à modéliser la structure en intégrant des non linéarités géométriques ou matérielles, on ne peut plus considérer de caractère stationnaire
On distingue ensuite les moyens de représenter les catégories de chargements :
-
Stationnaire :
-
Transformée de Fourier complexe (TF) ;
-
Densité spectrale de puissance (DSP) ;
-
Spectre de réponse d’oscillateur (SRO).
-
-
Transitoire :
-
Courbe de chargement de déplacement, vitesse ou accélération exprimée en fonction du temps ;
-
Effort ou pression exprimé en fonction du temps.
-
Deux grandes familles d’analyses peuvent être considérées :
-
L’analyse modale qui permet de connaître les fréquences propres et les modes propres d’une structure et servira pour caractériser :
-
la réponse au chargement stationnaire appliqué via une méthode de réponse spectrale ;
-
la réponse temporelle par intégration de Duhamel de chaque réponse modale à la courbe de chargement ;
-
une fonction de transfert convoluée au signal exprimé de manière fréquentielle pour délivrer une réponse en DSP ou TF.
-
-
La dynamique temporelle qui permet de calculer la réponse dynamique transitoire de la structure pour une excitation temporelle quelconque. Cette résolution est faite à l’aide de schémas d’intégration temporelle, qui peuvent être explicites ou implicites.
Les schémas explicites imposent de choisir des pas de temps très petits ; ils sont donc le plus souvent utilisés pour résoudre des problèmes sur des temps courts (type impact). Au contraire, les schémas implicites permettent d’utiliser des pas de temps plus grands et sont donc privilégiés pour étudier des plages temporelles plus grandes.
Exemples d’applications
| Applications | Représentation du chargement | Grandeurs accessibles | |
|---|---|---|---|
| Modal | Analyse vibratoire | TF | TF |
| DSP | DSP | ||
| Suivi de fréquence propre | SRO | Extrema spectraux de quantités d'intérêt variées | |
| Transitoire implicite | Etude sismique | Accélérations, vitesses, forces, pressions ou déplacements en fonction du temps | Quantités d’intérêts diverses exprimées au cours du temps |
| Ebranlement | |||
| Transitoire explicite | Chute d’un objet | Modélisation de projectiles en contact, chocs | Quantités d’intérêts diverses exprimées au cours du temps |
| Impact d’avion | Accélérations, vitesses, forces, pressions ou déplacements en fonction du temps |
Le problème dynamique une fois discrétisé par éléments finis se ramène à la résolution de l’équation d’équilibre suivante (cf. chapitre 1) :

-
M la matrice de masse exprimée aux nœuds,
-
C la matrice d’amortissement exprimée aux nœuds,
-
K la matrice de raideur exprimée aux nœuds,
-
q le vecteur des déplacements nodaux,
-
q' le vecteur des vitesses nodales,
-
q¨ le vecteur des accélérations nodales.
Dans le cas de l’analyse modale, on a recours au calcul des pulsations propres ω_i et des modes propres associés φ_i.
Dans le cas de l’analyse temporelle, on calcule à chaque instant t, par intégration directe des équations d’équilibre, les déplacements aux nœuds q(t) ainsi que les vitesses q'(t) et les accélérations q¨(t).
La seconde approche présente l’avantage de permettre de traiter des sollicitations non stationnaires.
B.1 Analyses reposant sur une recherche modale
B.1 Analyses reposant sur une recherche modale
B.2 Analyses reposant sur une intégration temporelle directe
B.2 Analyses reposant sur une intégration temporelle directe
B.3 Prise en compte de l'amortissement
B.3 Prise en compte de l'amortissement
B.4 Spécificités de l'analyse sismique
B.4 Spécificités de l'analyse sismique
$translationBooksB.1 Analyses reposant sur une recherche modale
B.1 Analyses reposant sur une recherche modale
Rappel sur la notion d’oscillateur simple – Notion de spectre de réponse élastique
Dans la suite de cette section, beaucoup de méthodes employées renvoient vers la réponse d’oscillateur amorti à un degré de liberté souvent dénommé oscillateur simple.
On rappelle très brièvement les grandes lignes de son comportement ici.
On se propose d’expliciter son comportement en reprenant l’équation de la dynamique appliquée à un oscillateur à un degré de liberté soumis à un chargement temporel harmonique et en bâtissant sa fonction de transfert paramétrée par le ratio entre sa pulsation propre et celle du chargement harmonique ainsi que son taux d’amortissement critique.
On rappelle l’expression de l’équilibre dynamique appliquée au système masse, ressort et amortisseur à un seul degré de liberté.

Qui s’écrit également sous forme canonique en divisant tous les termes par la masse m telle que :

Si on applique un chargement harmonique  , on peut trouver la fonction de transfert en réponse absolue en établissant le rapport entre ce chargement d’entrée et la réponse absolue de sortie ci-dessous :
, on peut trouver la fonction de transfert en réponse absolue en établissant le rapport entre ce chargement d’entrée et la réponse absolue de sortie ci-dessous :

La norme de cette fonction est l’amplitude de la fonction de transfert qui permet de mettre en évidence le phénomène d’amplification dynamique illustrée pour différentes valeurs de taux d’amortissement critique sur la figure 1. L’argument de cette fonction de transfert est la phase.
 Fonction de transfert
Fonction de transfert
Un spectre de réponse est différent d’une fonction de transfert. On appelle spectre de réponse élastique la courbe donnant l’accélération (dénommée spectrale) en fonction de la période (ou de la fréquence). Le spectre correspond à l’accélération absolue maximale vue par un oscillateur simple au cours du temps en fonction de sa période propre (ou de sa fréquence propre) et de son taux amortissement critique. Il dimensionne le mouvement sismique. Il est possible de construire une relation approchée entre le spectre de Fourier d’une accélération et le spectre en vitesse spectrale pour un taux d’amortissement nul.
A partir de l’équation de la dynamique de l’oscillateur simple soumis à une accélération quelconque :

On trouve les réponses maximales à partir de sa résolution en temps par une méthode de son choix (intégration de Duhamel, calcul direct …) puis par le calcul des valeurs dites spectrales de déplacement relatif, vitesse relative et accélération absolue :



La notion de pseudo-déplacement, vitesse ou accélération est souvent employée. Il s’agit d’une approximation de ces quantités à partir de l’une d’elle reposant sur le fait que le taux d’amortissement est assez faible (moins de 20%).


Un spectre peut se présenter sous la forme de la figure 2.
 Spectre
Spectre
Notion de base modale
On considère que la réponse de la structure s’appuie sur une combinaison de réponses harmoniques. A ce titre, les réponses harmoniques sont des champs solutions q(t) de l’équation :

Ils peuvent donc s’écrire sous la forme :

Si l’on fait l’hypothèse de Basile (on néglige C), on arrive à rechercher les solutions de l'équation algébrique :

Si l’on ne fait pas l’hypothèse de Basile, cela revient à rechercher les modes complexes ; on postule :

et on résout le problème aux valeurs propres :

Pour y parvenir, sans négliger C, il a fallu poser :


Avec les matrices A et B telles que :
 et
et 
On désigne aussi par γ le vecteur tel que :

On recherche les solutions sous la forme de paires d’harmoniques complexes conjuguées telles que :

avec :
-
ψi qui est un vecteur déformée modale complexe,
-
λi qui est une fréquence propre complexe.
Dans tous les cas, réel ou complexe, on a donc à résoudre une équation en λi2 de même degré N (2N pour les cas complexes) que l’ordre de la matrice N (2N pour les cas complexes). L’ordre de cette matrice est égal au nombre de degrés de libertés du système discrétisé (le double pour les cas complexes). L’équation évoquée n’est autre que les cas de nullité du déterminant de cette matrice et donc de son polynôme caractéristique.
A des fins de simplification, on considère par la suite le cas de modes réel avec l’hypothèse de Basile.
A chaque pulsation ωi est associé un vecteur propre. Celui-ci va être recherché en fixant une de ses composantes à 1, puis un système à n-1 paramètres est résolu.
Attention : les modes sont donc définis à une constante multiplicative près, d’autant qu’ils sont par la suite normés au moyen de procédés variables. Le plus courant pour les codes EF est de normer les modes au moyen de la matrice masse ; ce point est détaillé par la suite. Ils peuvent être également normés par leur plus grand déplacement modal.
Les modes propres ont la propriété d’être orthogonaux pour la matrice de masse, ce qui se formule comme suit :

En l’absence de chargement, les modes n’ont aucun sens physique. On peut donc choisir de les normer de différentes façons pour rendre leur visualisation compréhensible. A ce titre, il est le plus souvent rencontré dans les codes EF :
-
de normer les modes sur la matrice masse, on a alors :

-
de normer les modes à partir d’un mode en particulier.
Pour les cas où le code ne norme pas cette valeur, on désigne cette grandeur par le terme de masse généralisée et on écrit pour le mode i :
L’objet de ce document étant de traiter des études conduites par les codes EF, on retiendra que les modes sont normés sur la matrice masse et donc la masse généralisée est toujours égale à l’unité.
On construit également la grandeur appelée masse modale qui permet d’identifier la quantité de masse de la structure entraînée par un mode dans une direction donnée Δk:

Attention : la masse modale est une grandeur bien différente de la masse généralisée comme l’équation ci-dessus permet de le mettre en évidence.
Utilisation de la base modale
Réponse temporelle par projection sur base modale
Une solution à l’équation globale :

peut être décomposée sur la base de vecteurs propres orthogonaux en N problèmes indépendants qui sont ceux décrivant la réponse d’un oscillateur simple ri(t) :
Pour les cas de séisme, le chargement f(t) est un chargement inertiel appliqué à l’ensemble de la structure :
 .
.
Analyse harmonique
On s’intéresse dans ce type d’analyse à construire une fonction de réponse en fréquence de la structure aux différents nœuds du modèle. Cette réponse peut être une quantité d’intérêt quelconque (déplacement, vitesse, accélération – absolus ou relatifs –, efforts …) en fonction d’une gamme de chargements harmoniques d’entrée qui peuvent également être décrits de différentes façons semblables à la quantité d’intérêt extraite.
Le chargement imposé sur un ensemble quelconque de nœuds de la structure est dans ce cas précis une harmonique du type :
 .
.
Le résultat de l’analyse en tout nœud de la structure est une fonction de transfert complexe dont la norme (l’amplitude) et l’argument (la phase) sont le plus généralement utilisés. Ils permettent d’identifier les résonnances de la structure ou de l’équipement et de connaître l’amplitude de sa réponse à différents chargements harmoniques.
Troncature de base modale – Cas général
En règle générale, comme on ne peut pas extraire par calcul tous les modes (trop coûteux et long, voire numériquement inatteignable dans certains cas), il faut se contenter de ceux susceptibles de répondre au chargement de la structure.
Si la fréquence représentative retenue pour le chargement est fc (Hz) on cherchera à extraire les modes jusqu’à 2 fc.
Il est important également de veiller à bien représenter les modes susceptibles de contribuer localement.
Une recherche de mode ne doit pas s’accompagner d’une lecture de valeurs de fréquences mais d’une visualisation de leurs déformées.
$translationBooksB.2 Analyses reposant sur une intégration temporelle directe
B.2 Analyses reposant sur une intégration temporelle directe
Les schémas d'intégration
Grands principes
Le principe des différentes méthodes d’intégration directe est de découper l’intervalle d’étude en n intervalles de longueur ∆t = T/n et de vérifier l’équilibre aux instants discrets Ti = i ∆t = i T/n. La différence entre les différentes méthodes (différences centrées, Wilson, Newmark…) repose sur l’hypothèse qui est faite sur la variation des grandeurs cinématiques sur l’intervalle ∆t.
Schéma explicite :
Si la valeur de déplacement peut être calculée directement à partir de la ou des valeurs au pas de temps précédents, la résolution est dite explicite. Dans ce cas, l’équilibre est considéré en début d’incrément.
Schéma implicite :
Les méthodes implicites sont celles pour lesquelles l’équilibre doit être considéré à la fin de l’intervalle, ce qui nécessite la résolution d’un système linéaire.
Comme indiqué plus haut, il existe un grand nombre de schémas d’intégration et l’objectif n’est pas ici d’en faire une description exhaustive (voir pour cela des ouvrages spécialisés). Nous nous contentons d’en présenter deux, la méthode des différences centrées, méthode explicite conditionnellement stable et la méthode de Newmark, schéma inconditionnellement stable (pour les problèmes linéaires).
Un schéma est dit inconditionnellement stable si, pour n’importe quelles conditions initiales, la solution reste bornée quel que soit le pas ∆t choisi , en particulier lorsque ∆t/T est grand. Par opposition, une schéma est conditionnellement stable si la solution obtenue reste bornée seulement si ∆t reste inférieur à une valeur limite ∆tcrit.
La précision est un concept différent de la stabilité, qui prend toute son importance pour les schémas inconditionnellement stables. Au-delà des inévitables erreurs d’arrondi, la précision agit sur deux sources d’approximations : un allongement (artificiel) de la période et une diminution de l’amplitude. L’influence de ces deux phénomènes augmente avec l’augmentation de ∆t mais de manière indépendante.
Méthode des différences centrées
Il s’agit d’un schéma de type différences finies reposant sur l’approximation de l’accélération (développement de Taylor au second ordre) :

Pour obtenir le même ordre d’erreur sur la vitesse, on utilise :

Les déplacements à l’instant t+∆t sont obtenus en considérant l’équilibre à l’instant t :

Soit, en introduisant les approximations de l’accélération et de la vitesse :

De la forme :

Cette méthode nécessite une procédure de démarrage afin de calculer q(-∆t) (à partir de l’équilibre à t=0). L’amortissement introduit par ce schéma est nul (pas de décroissance d’amplitude).
Méthode de Newmark
Ce schéma repose sur les approximations suivantes de la vitesse et du déplacement en fin d’intervalle :

![]()
De la valeur des 2 paramètres α et δ (compris entre 0 et 1) dépendent la précision et la stabilité de la méthode : le couple (δ = 1/2 et α = 1/4) conduit au schéma inconditionnellement stable appelé méthode de Newmark : il correspond à considérer l’accélération moyenne constante. En considérant l’équilibre à la fin de l’intervalle d’étude (à l’instant t+Δt), on obtient :

avec

et
![]()
les coefficients étant définis ci-dessous :
![]()
Ce schéma nécessite également une procédure de démarrage : la valeur de q ̈(0) est obtenue en considérant l’équilibre à t=0. Comme la méthode des différences centrées, le schéma de Newmark de base (δ = 1/2 et α = 1/4) n’introduit pas d’amortissement numérique. Le couple (α = 0, δ = ½) permet de retrouver la méthode des différences centrées.
Choix de la discrétisation spatiale et temporelle
Critère sur les tailles d’éléments satisfaisant les longueurs d’ondes
Différents critères peuvent intervenir qui sont directement liés à la précision des résultats attendus et au type de calcul qui est entrepris.
Pour les analyses transitoires, la recommandation généralement retenu est d’avoir de l’ordre de 8 à 10 éléments par longueur d’onde. Les ondes stationnaires étant constitués de la somme d’ondes propagatives, les analyses en dynamique stationnaire (cas des séismes typiquement) verront s’appliquer le même type de critère.
On rappelle l’expression générale reliant longueur d’onde λ, fréquence f et célérité c de l’onde ou encore la pulsation ω est :

En fonction des types d’éléments utilisés et du type d’onde qui retient notre intérêt, on retiendra les différentes formulations suivantes :
Éléments volumiques dans un milieu isotrope (cas type d’une modélisation d’un sol élastique de module E, de coefficient de Poisson ν et de masse volumique ρ) :
-
Onde de cisaillement :

-
Onde de compression :

Éléments coques isotropes :
-
Onde de flexion :
 où h est l’épaisseur de la coque, D le coefficient de raideur flexionnel.
où h est l’épaisseur de la coque, D le coefficient de raideur flexionnel. -
Onde de cisaillement :

-
Onde de compression :

Ces formulations s’écrivent plus généralement de la façon suivante pour un milieu anisotrope avec 2 directions principales 1 et 2 :
-
Onde de flexion :

-
Onde de cisaillement :
 (expression valable en coque et plaque et en volume),
(expression valable en coque et plaque et en volume), -
Onde de compression :
 (expression valable en coque et plaque et en volume).
(expression valable en coque et plaque et en volume).
On peut trouver la taille requise pour cibler une fréquence de coupure de 40 Hz dans des éléments coques et plaques ou dans des éléments volumiques. La taille requise est donnée par le nombre ci-dessous / λ pour 10 éléments.
| Types de modélisations | Fréquence cible [Hz] | Epaisseur [m] | Type d'onde | Coeff de taille d'élément |
|---|---|---|---|---|
| Coques et briques - GC Béton | 40 | 0,2 | Flexion | 0,59 |
| 40 | 0,25 | Flexion | 0,66 | |
| 40 | 0,5 | Flexion | 0,93 | |
| 40 | 1 | Flexion | 1,32 | |
| 40 | 1,5 | Flexion | 1,61 | |
| 40 | - | Cisaillement | 6,04 | |
| 40 | - | Compression | 6,75 | |
| Coques et briques - Méca Acier | 40 | 0,01 | Flexion | 0,16 |
| 40 | 0,02 | Flexion | 0,22 | |
| 40 | 0,1 | Flexion | 0,50 | |
| 40 | - | Cisaillement | 8,02 | |
| 40 | - | Compression | 9,58 |
Ce critère n’est pas nécessairement suffisant et, pour les cas où une analyse temporelle par projection sur base modale ou une réponse spectrale est recherchée, une analyse de sensibilité doit être mené afin d’observer si un raffinement de maille conduit à faire varier significativement les facteurs de participation modaux (ou alors la masse modale si ce critère est scruté). Ces éléments sont décrits plus loin dans ce chapitre et leur lien sont exposés.
Critère sur les pas de temps
Les schémas temporels conditionnellement stables comme le schéma des différences centrées doivent satisfaire une condition sur le pas de temps choisi. On appelle souvent cette condition la condition CFL (Courant-Friedrichs-Levy).
| Cas non amorti | Cas amorti |
| Satisfait pour |
Satisfait pour |
Exemple d’application pour un modèle de treillis métallique dont le plus petit élément est de longueur L :
On considère un élément barre à 2 nœuds notés 1 et 2.
Les barres sont de longueur L, de section A et de masse volumique ρ et de module d’Young E.
On considère la matrice masse telle que la masse totale est répartie également aux deux extrémités.
Les matrices K et M s’expriment respectivement sous la forme :
![]() et
et 
Le polynôme caractéristique s’exprime tel que :
![]()
Ce qui conduit à :

Comme la vitesse de propagation des ondes de compressions dans un milieu continu s’exprime par :

On trouve que :
 et
et  soit
soit 
Dans un modèle dont le maillage n’est pas régulier, c’est le plus petit pas de temps qui pilote le pas temps global.
B.3 Prise en compte de l'amortissement
B.3 Prise en compte de l'amortissement
L’amortissement des amplitudes des phénomènes vibratoires d’une structure est lié à des phénomènes dissipatifs d’origines très variées qui peuvent se produire au sein de la structure. Il peut s’agir de phénomènes visqueux propres à des amortisseurs fluides que l’on peut trouver dans des boîtes à ressort ou des amortisseurs (isolateurs à câble, amortisseur de type JarretTM, amortisseur à fluide visqueux). Il peut s‘agir également de phénomènes de dissipation structurelle liés à des états de fissurations et aux frottements aux interfaces des matériaux. L’énergie est consommée dans les hystérésis de comportement des matériaux.
Dans l’essentiel des cas, la prise en compte de l’amortissement s’opère dans les calculs dynamiques au travers d’une matrice d’amortissement visqueux C. Les termes de cette matrice peuvent être localement définis exactement pour les cas où l’amortissement est totalement maîtrisé parce qu’il s’agit d’équipements amortissants dont on connaît les caractéristiques. Mais la plupart du temps, pour les structures de GC, il est rare de connaître le terme d’amortissement compte tenu de l’hétérogénéité des structures et du caractère non visqueux des matériaux eux-mêmes.
On préfère construire cette matrice à partir des taux d’amortissement critique, définis réglementairement pour les différents matériaux. Ces taux sont définis avec une hypothèse de comportement visqueux proportionnel à la vitesse de sollicitations ; il s’agit d’une fraction de la valeur d’amortissement critique qui conduit pour un oscillateur simple à un retour à l’équilibre sans passer par un régime d’oscillations.
Pour les cas où les termes d’amortissement sont connus, la matrice C est construite explicitement et il est nécessaire d’avoir recours à une méthode de calcul temporel dédiée, afin de bien respecter les caractéristiques de celle-ci :
-
soit avec un calcul par intégration directe : il s’agit de résoudre l’équilibre dynamique à chaque instant en ayant discrétisé le temps,
-
soit avec un calcul par projection sur base modale, faisant appel à des modes complexes.
Les analyses de phénomènes de dynamique rapide (explosion, impact) doivent faire l’objet de considérations spécifiques.
En effet, il n’est pas nécessaire de considérer d’amortissement pour les études de vérifications locales de résistance ou de vibrations sur des temps trop courts pour « activer » des réponses harmoniques de la structure. On peut donc se passer pour ces cas de prendre en compte l’amortissement.
Il convient par ailleurs de noter que ce genre de calculs, effectués par des codes de dynamique faisant appel à des schémas d’intégration temporelle dit explicite (LS-Dyna, Radioss, PAM-Crash, Europlexus, …) n’ont pas recours à une résolution classique faisant intervenir une « inversion » de la matrice de rigidité. Pour les analyses de vibrations induites sur une fenêtre de temps succédant la durée du choc, il est par contre nécessaire de caractériser l’amortissement.
Nota : dans des calculs de dynamiques rapides (quelques millisecondes), le terme d’amortissement est généralement négligé car son ordre de grandeur est très inférieur à celui des termes inertiels et de rigidité locale sur le temps très court où le phénomène est analysé.
Pour les cas plus « classiques », on a généralement recours à une construction de la matrice d’amortissement à partir des taux d’amortissement critique définis pour les matériaux et par combinaison linéaire des matrices M et K qui ont déjà été élaborées par le code de calcul aux éléments finis. Cette démarche permet de simplifier considérablement les étapes de calcul. Cette approche est liée à l’hypothèse dite « de Basile » pour les analyses modales. Cette hypothèse a été formulée dans le cadre de l’identification de l’amortissement structurel (principalement en aéronautique), et est restitué comme suit :
« Même en présence de couplage modal d’amortissement, les équations modales du mouvement sont dynamiquement découplées, pour les structures faiblement amorties, si la séparation des modes en fréquences est satisfaisante ».
Attention : prendre en compte l’hypothèse de Basile conduit à sous-évaluer la réponse dynamique ailleurs qu’à proximité des matériaux ou points d’appuis qui présentent un amortissement élevé par rapport à un calcul temporel par intégration directe ou à l’utilisation de méthodes plus sophistiquées comme celles des modes complexes. Ceci justifie le fait d’avoir recours à un calcul par intégration directe des équations de mouvement ou en faisant appel à des modes complexes.
Le plus souvent, l’hypothèse de Basile est considérée et la matrice est construite à partir de la méthode de Rayleigh.

Les termes α et β sont à caler. De manière pragmatique, la démarche qui suit doit être prise en compte. On considère :
 , soit exprimé en fréquence :
, soit exprimé en fréquence : ![]() ,
,
 , soit exprimé en fréquence :
, soit exprimé en fréquence : ![]() ,
,
f1 étant une valeur inférieure au premier mode significatif de la structure, et fn le premier mode rencontré après la coupure du spectre de réponse élastique caractérisant le signal temporel appliqué. On reconstitue pour toute valeur de ω la valeur de l’amortissement réduit, en faisant appel à la formule ci-dessous :
 , soit exprimé en fréquence :
, soit exprimé en fréquence : 
Attention : l’amortissement étant très largement surévalué au-delà des 2 fréquences d’intérêt, il est nécessaire de maîtriser ces deux valeurs. Si fn a bien été choisie, la surévaluation de l’amortissement est sans conséquence car on trouve sur ces plages de fréquences des modes de corps rigides qui seront sollicités dans la réponse et les modes au-delà de la fréquence de coupure sont insensibles à l’amortissement. Mais il faut être sûr pour cela que l’on ne prête pas attention à d’éventuels modes locaux à haute fréquence.
L’impact d’une erreur dans le choix de la première fréquence peut être plus lourd de conséquences si un mode significatif a été oublié car sa réponse sera dès lors négligée.
Il importe de noter qu’entre les deux fréquences, l’amortissement est sous-évalué. On a en ce cas une évaluation conservative de la réponse de la structure.
B.4 Spécificités de l'analyse sismique
B.4 Spécificités de l'analyse sismique
Réponse spectrale - Cas spécifique du séisme
Le principe de la méthode est, pour une direction de séisme de donnée, de construire les réponses maximales à partir du spectre de chargement en tout point considéré mode par mode, puis de les cumuler entre elles par différentes méthodes.
Une fois obtenue la réponse sismique pour une direction donnée, les directions sismiques sont combinées entre elles pour avoir la réponse globale.
On se place dans un cas où les vecteurs modaux sont normés au moyen de la matrice de masse, i.e. dans le cas de la plupart des codes de calcul aux éléments finis.
On peut écrire l’expression pour un degré de liberté sous la forme canonique :
Le terme pik est appelé coefficient participatif. Il s’agit d’une notion importante dans le cas de l’analyse sismique car elle restitue la contribution physique d’une excitation dans une direction k donnée.
Elle est déterminée pour les cas où l’on norme les vecteurs propres sur la matrice masse par :
D’autre part, on connaît pour un mouvement sismique ![]() donné, dans une direction sismique
donné, dans une direction sismique ![]() , les solutions majorant en moyenne les valeurs maximales de
, les solutions majorant en moyenne les valeurs maximales de ![]() ,
, ![]() et
et ![]() en termes de pseudo-accélérations, pseudo-vitesses et déplacements via les spectres respectifs de ce mouvement :
en termes de pseudo-accélérations, pseudo-vitesses et déplacements via les spectres respectifs de ce mouvement :

Cette réponse est construite pour un amortissement modal ξi qui peut être évalué au prorata de l’énergie de déformation modale (voir §1.2.1 de Génie parasismique Tome 3, J. Betbeder-Matibet).

où :
-
EiT est l’énergie de déformation totale de la structure pour le mode i telle que :

-
Ei matériau j est l’énergie de déformation dans la structure dont l’amortissement matériau est ξj.
Ensuite à partir de la réponse de l’oscillateur simple, on reconstruit la réponse pour chaque mode, respectivement en accélération, vitesse et déplacement, dans la structure au moyen de :

Ces grandeurs modales doivent ensuite être combinées entre elles pour une direction de chargement donnée afin d’obtenir la réponse complète de la structure. Il existe diverses méthodes de recombinaison (par la suite la notation ak,p désigne à titre d’exemple la composante p du vecteur ai,k, il en va de même pour φi,p à partir de φi) :
-
Racine carrée de la somme des carrées, dit « cumul quadratique simple » ou également « SRSS : Square Root of the Sum of the Square » – En chaque nœud p :

-
Cumul quadratique complet (dit CQC) – En chaque nœud p :

où le terme Pij désigne le coefficient de couplage quadratique des modes i et j. Il s’écrit :

Il importe de noter que, dans cette combinaison, il s’agit d’un cumul de termes algébriques mais dont le signe est toujours positif et ne pose donc pas de difficulté à être placé sous la racine.
En considérant des amortissements modaux ξi et ξj égaux à une valeur variable telle que x = {0.2, 4, 7, 20 et 30%}, on peut tracer pour des ratios de pulsations ωi/ωj le graphique de la figure 3 qui permet de faire apparaître que les modes voisins se cumulent très nettement tandis que le coefficient de cumul diminue assez rapidement lorsque ce ratio croît et ceci d’autant plus lorsque l’amortissement est faible.

Illustration du coefficient de couplage pour des taux d’amortissements variables en fonction des ratios de pulsation
Ce dernier constat milite pour l’utilisation d’un cumul CQC lorsque des modes sont assez proches car le cumul SRSS ne prendrait pas en compte le cumul des modes proches.
En revanche, il n’y a aucune plus-value à utiliser un cumul CQC par rapport à un SRSS lorsque les modes sont éloignés les uns des autres.
Attention : Les réponses modales cumulées ne doivent pas être utilisées pour calculer d’autres quantités d’intérêt. A titre d’exemple il ne faut pas surtout pas évaluer les efforts issus des réponses CQC en calculant  : cette évaluation est erronée par rapport à l’évaluation par cumul des efforts modaux.
: cette évaluation est erronée par rapport à l’évaluation par cumul des efforts modaux.
Il faut donc pour cet exemple précis dérouler le calcul comme suit :
-
 ,
, -
Pour chaque terme p du vecteur fk, on écrit :
 ,
,
Il est aussi important de garder à l’esprit que de la même manière des critères permettant d’évaluer des états de fissurations sur la base des invariants du tenseur des contraintes, et donc des contraintes principales, (cf. par exemple le critère proposé dans l’annexe LL de l’EN1992-2) ne peuvent être considérés au terme d’un calcul avec un cumul quadratique de quelque nature que ce soit.
Les réponses spectrales de chaque mode une fois cumulées pour une direction de chargement sismique doivent être combinées afin d’obtenir la réponse totale. On parle dans ce cas de cumul spatial.
Les cumuls spatiaux peuvent s’opérer selon diverses méthodes :
-
Par racine carré de la somme des carrés des réponses obtenue dans chaque direction. Cette méthode fait perdre le signe et toute concomittance logique des sollicitations. Elle fournit une seule quantité scalaire pour chaque quantité d’intérêt :

-
Par cumul algébrique de type « Newmark ». Cette approche repose sur une hypothèse d’indépendance les unes aux autres de chaque réponse spatiale et pondère d’un coefficient μ, dont la valeur varie suivant les standards, les 2 autres réponses défavorablement par rapport à celle d’une direction privilégiée. Elle prend en compte la variabilité de signe de chaque quantité d’intérêt. Elle conduit donc non pas à une seule réponse cumulée mais à 24 au total comme cela est compréhensible dans l’équation suivante :

Troncature de base modale – Cas du séisme
Pour le cas spécifique du séisme et en retenant une norme des modes par la matrice masse, il vient :

Il s’agit de la masse entraînée pour un mode i dans une direction k. Cette masse est donc liée à une direction spécifique, pour un mode i il y aura donc 3 masses modales en fonction des différentes directions de sollicitation (si on est dans l’espace, 2 dans le plan et une seule pour un problème unidimensionnel), la figure 4 apporte une illustration en 2D pour un portique.
Les déformées modales multipliées par les coefficients participatifs représentent la déformée de la structure dont le produit en tout point avec la réponse d’un oscillateur simple fournit la réponse au cours du temps pour un mode déterminé. Ceci est détaillé dans le chapitre suivant.

Illustration schématique des entraînements de masse pour un même mode suivant 2 directions différentes
Comme on l’a évoqué plus haut si le modèle possède N degrés de libertés, il y aura au plus N modes propres.
Toutefois, dans la mesure où la recherche des fréquences et modes propres fait l’objet d’une démarche numérique, tous les modes ne sont pas extraits. En théorie, on doit avoir :
 , ou
, ou  ou
ou 
En pratique, le code va s’arrêter à une limite fixée par l’utilisateur au travers d’une fréquence maximale d’extraction. Puis l’utilisateur doit vérifier qu’il en dispose d’un nombre suffisant pour restituer un pourcentage de masse fixé par la règle d’ingénierie qu’il applique. Le plus généralement ce critère est de 90 % de la masse.
Attention : Si, à la fréquence de coupure, le pourcentage de masse ciblée n’est pas atteint, il peut être nécessaire de faire appel à un pseudo-mode.
Inversement si un pourcentage de masse important est atteint à une fréquence très basse, très en-dessous de la fréquence de coupure, il est nécessaire de faire appel à un pseudo-mode ou de compléter la base modale. En effet, la masse participante d’un plancher pour un mode de flexion local sur un très grand ouvrage représente une très faible fraction de la masse totale.
Attention également aux modes antisymétriques dont la masse modale peut être nulle car les masses entraînées autour d’un axe de la structure se compensent.
Pseudo-mode ou correction statique
Comme on l’a formulé précédemment, le critère de sélection des modes propres porte sur le cumul de la masse modale fixé à 90 % pour une fréquence de l’ordre de la fréquence de coupure du spectre sismique i.e. 40 Hz max.
Lorsque cette valeur n’est pas atteignable, le pourcentage plus faible retenu va être complété d’une masse additionnelle associé à un « pseudo-mode » de vibration.
On rappelle que l’on a pour une direction de séisme k une réponse cumulée sur n modes :

En toute rigueur, s’il y a N degrés de libertés, cette formulation serait :

Comme l’on a vu précédemment, les modes au-delà de la fréquence de coupure sont des modes rigides. La structure réagit en phase avec le chargement sismique qui lui est appliqué avec un déplacement relatif nul.
Pour compléter la base modale, on construit les pseudo-modes en considérant que la réponse totale est la somme de la réponse « dynamique » prenant en compte la base modale sur les n premiers modes retenus et d’un terme proportionnel à l’accélération sismique du support q̈s(t). On retient les expressions suivantes :

où Pk est la déformée dans la direction k de la structure soumise au chargement statique équivalent à la masse de la structure accélérée à l’accélération correspondante au dernier mode extrait de pulsation n :

Comme la réponse en accélération relative pour la structure est nulle au-delà de la fréquence de coupure, on peut simplement écrire :

En reprenant la formule précédente en fonction de  , on pourra plus facilement faire le lien dans le cadre des analyses spectrales avec le spectre de pseudo-accélérations :
, on pourra plus facilement faire le lien dans le cadre des analyses spectrales avec le spectre de pseudo-accélérations :

On considère donc également la formule :

Une fois ces grandeurs vectorielles évaluées, se pose la question de leur cumul.
En effet, la solution temporelle pour une direction de séisme est donnée via la recombinaison des composantes sur la base modale :
En revanche, cette combinaison n’est pas applicable sur les grandeurs maximales que nous venons d’évaluer.
$translationBooksChapitre C - Calculs statiques non-linéaires
Chapitre C - Calculs statiques non-linéaires
Les calculs non-linéaires sont généralement longs : un programme d’éléments finis les résout comme une succession de problèmes linéaires enchaînés (processus incrémental). La préparation de tels calculs demande à l’utilisateur de faire des choix, comme la définition des incréments, le choix d’un algorithme, etc. Le traitement exige donc une certaine expérience d’utilisation du logiciel.
Avant de se lancer dans un calcul non-linéaire, il importe au préalable de préciser ce que l’on en attend : cela permet en effet de savoir quand arrêter le calcul ; car la plupart des calculs non-linéaires peuvent être a priori poursuivis jusqu’à l’apparition d’un ou plusieurs mécanismes ou, dans le cas de problèmes de contact, jusqu’à la disparition du nombre minimum de liaisons (ou d’appuis).
C.1 Les problèmes de mécanique non-linéaire
C.1 Les problèmes de mécanique non-linéaire
C.2 Pourquoi exécuter des calculs non-linéaires ?
C.2 Pourquoi exécuter des calculs non-linéaires ?
C.3 Mise en œuvre
C.4 Problèmes de convergence ? Symptômes et solutions
C.4 Problèmes de convergence ? Symptômes et solutions
$translationBooksC.1 Les problèmes de mécanique non-linéaires
C.1 Les problèmes de mécanique non-linéaires
1) Description des non-linéarités potentielles
La non-linéarité d’un problème de mécanique vient de ce que les coefficients apparaissant dans l’équation d’équilibre dépendent de la déformation du solide à l’équilibre. Autrement dit, l’équation d’équilibre est généralement une équation de type implicite.
Il existe plusieurs catégories de non-linéarités pour les problèmes de mécanique statique :
-
Les non-linéarités matérielles : c’est le cas dès lors que la loi de comportement n’est pas linéaire ou que la réponse dépend de l’histoire du chargement. Autrement dit, la contrainte n’est pas une fonction linéaire de la déformation. L’exemple le plus fréquent en génie civil est celui des matériaux sollicités au-delà de leur limite élastique, et qui développent un comportement élasto-plastique. Ce comportement se caractérise par une dépendance de la raideur du matériau vis-à-vis de son état de contrainte.
-
Les non-linéarités géométriques : c’est le cas dès lors qu’on travaille en grands déplacements ou en grandes déformations. Dans le premier cas, on ne peut plus écrire le problème en négligeant les changements de configurations. Dans le second cas, on ne peut plus approcher la déformation par un simple gradient du déplacement.
-
Les non-linéarités des conditions aux limites : cela peut être le cas, lorsque chargement est progressif, lorsqu’il y a contact potentiel entre 2 corps, dans le cas de force suiveuse, mais aussi lorsqu’on simule le phasage de construction, ou le lançage d’un tablier, le creusement d’une galerie, la mise en remblai, etc.
Ces types de non-linéarités peuvent être couplés, si le code de calcul le permet, mais cela complexifie d’autant la résolution du problème.
2) Principe de résolution d'un problème non-linéaire : Méthode de Newton
Lorsqu’on résout le problème élément fini, on cherche le champ de déplacement u, tel que les efforts intérieurs Lint soient égaux aux efforts extérieurs Lext :
 , qui est un problème non-linéaire en fonction de u.
, qui est un problème non-linéaire en fonction de u.
Pour résoudre un problème de statique non-linéaire, on utilise généralement un algorithme incrémental. Pour cela le problème est paramétré en fonction d’un paramètre t (qui est un pseudo-temps, contrairement aux calculs dynamiques). Ce paramètre sert à indexer les chargements successifs imposés à la structure. Plus précisément, on va chercher l’état d’équilibre correspondant aux chargements successifs F1, F2, …
Ce découpage conduit à résoudre une succession de problèmes quasi-linéaires comme illustrée sur la figure ci-dessous, et à déterminer l’état de la structure à l’instant t (déplacements, déformations, contraintes) en connaissant la solution à l’état t-1. Plus le nombre de découpage est important, meilleure est la précision.


Principe du paramétrage de problème en fonction de t
A chaque incrément ti, le problème discrétisé à résoudre est : Ki x qi =Fi où qi est le vecteur déplacement inconnu sous le chargement imposé Fi. Alors que dans le cas linéaire vu au chapitre 1, la matrice K était explicite, lorsque le problème est non-linéaire, Ki est une matrice dont les termes dépendent implicitement de la valeur de qi. Déterminer qi ne peut donc pas se faire directement en inversant la matrice K.
La méthode la plus courante pour résoudre cette équation non-linéaire est d’utiliser un algorithme de type Newton. Le principe est de construire une bonne approximation de la solution de l’équation  en considérant son développement de Taylor au premier ordre
en considérant son développement de Taylor au premier ordre  . On part donc d’un point initial (suffisamment proche de la solution) et on construit par récurrence la suite
. On part donc d’un point initial (suffisamment proche de la solution) et on construit par récurrence la suite  .
.
A chaque itération, on évalue le vecteur résidu F(qk) et on poursuit tant que celui-ci n’est pas inférieur (en norme) à une valeur arbitrairement proche de 0. Ce critère de convergence doit être choisi avec soin en fonction de la norme utilisée par le code de calcul (voir §3.3 pour plus de détails).
Remarque : Avec la méthode de Newton, à chaque itération, on doit calculer la matrice tangente au point considéré  .
.
Le coût de calcul de cette matrice peut être coûteux en temps. Si l’utilisation de cette matrice permet d’avoir une convergence quadratique (donc en peu d’itérations), il n’est pas indispensable d’utiliser cette matrice. D’autres stratégies peuvent être appliquées pour estimer cette matrice. On parle alors de méthode de quasi-Newton. Ainsi il est ainsi envisageable d’utiliser la matrice tangente sans la réactualiser à chaque itération mais aussi d’utiliser la matrice élastique (figure b) ou la matrice sécante dans les cas de modèle endommagement. Une illustration des itérations successives selon la matrice utilisée est proposée sur la figure ci-dessous.

Illustration de la méthode de Newton ou quasi-Newton (matrice élastique)
En règle générale, l’utilisation de la matrice tangente permet une convergence plus rapide (en moins d’itérations), mais les variantes peuvent être plus efficaces ou plus robustes selon les situations.
La méthode de résolution étant itérative, le processus doit être interrompu lorsque le critère d’arrêt est atteint, c’est-à-dire que l’on a vérifié qu’une grandeur (plusieurs définitions sont possibles) devient négligeable. L’algorithme global est le suivant :

en désignant les incréments, i indexant les itérations de Newton et ε étant une valeur positive, proche de 0.
Remarque : l’algorithme de Newton est utilisé pour résoudre l’équilibre à chaque pas de temps. Il peut être également utilisé pour trouver la contrainte en chaque point de Gauss (à toutes les itérations du problème de Newton à l’échelle globale) lorsque la loi de comportement le nécessite.
$translationBooksC.2 Pourquoi exécuter des calculs non-linéaires ?
C.2 Pourquoi exécuter des calculs non-linéaires ?
Comme dans bien des domaines de la physique, il n’est raisonnable d’entreprendre un calcul non-linéaire qu’une fois que l’on a au moins une petite idée de la « fin de l’histoire », c’est-à-dire de la façon dont la structure va évoluer au point de devenir instable. Nous présentons ci-dessous les raisons pouvant justifier un calcul non-linéaire, en distinguant les bonnes de certaines plus discutables…
1) Bonnes raisons
-
Étudier la redistribution des efforts. Une fois que certaines parties d’une structure sont entrées en plasticité, le niveau de contrainte y est, en un certain sens, à peu près « gelé » à une valeur déterminée, et le travail des actions extérieures ne peut plus être dissipé qu’en augmentant le niveau de contrainte ailleurs, ou en faisant s’écouler la matière des zones déjà plastiques. Le but est ici de vérifier dans quel ordre les éléments d’une structure « lâchent », et d’appréhender le mécanisme de ruine final.
-
Déterminer l’évolution des conditions d’appui d’une structure, soit par un calcul de contact, soit par formation de rotules plastiques internes.
-
Sans aller jusqu’à s’intéresser à la redistribution des efforts, obtenir un état d’équilibre où, dans les zones plastiques, les contraintes sont, en moyenne, proches de la contrainte d’écoulement du matériau, et où les contraintes sont bien dans le domaine élastique ailleurs. Pour les géomatériaux, obtenir un état d’équilibre où les contraintes sont, sauf en quelques zones très ponctuelles, des contraintes de compression (éliminer les tractions).
Ces démarches sont raisonnables, car :
-
elles peuvent être menées généralement dans le cadre fondamental des petites déformations,
-
elles permettent une simplification de la modélisation, et donc une lecture simple de la mécanique de la structure : les zones plastifiées, en effet, n’ayant plus de rôle porteur, on peut proposer une analyse de l’affaiblissement de la structure par une succession de calculs élastiques phasés, en « désactivant » à certains niveaux de chargement, les zones plastifiées ; l’analyse des zones plastiques peut aussi suggérer une approche statique de la plastification (modèle bielles et tirants).
2) Raisons discutables
-
connaître l’aspect de la structure très déformée (et même en train « d’exploser »), éventuellement en utilisant l’algorithme de remaillage automatique fourni avec le logiciel,
-
faire un calcul avec un comportement a priori très riche du point de vue descriptif, pour voir si ça sert à quelque chose, ou si on comprend mieux le résultat qu’avec le calcul élastique fait précédemment.
Ces motivations sont de celles qui aboutissent le plus souvent à des problèmes de non-convergence ou de « pivot nul » (cf. ci-après). Lorsque l’on interrompt le calcul, faute de mieux, à une étape du processus itératif, la déformée de la structure (donnée par la déformée du maillage, ou le champ des déformations) est illusoire :
-
les déformations sont généralement supérieures à 1 %, donc à ce stade le problème mécanique n’est plus écrit dans les bonnes variables ;
-
la déformation calculée dépend du maillage de façon critique, c’est-à-dire que pour deux maillages initialement voisins, on peut obtenir des valeurs de déformation locale très différentes ;
-
le programme de calcul ne « suit » par définition qu’une instabilité à la fois ; or les problèmes de grands déplacements sont par nature multi-branches, c’est-à-dire qu’à un certain stade, il existe plusieurs configurations d’équilibre possibles pour un chargement donné…
C.3 Mise en œuvre
C.3 Mise en œuvre
La bonne méthode consiste toujours à procéder par étape et à ne pas introduire toutes les non-linéarités simultanément :
-
faire un premier calcul avec une loi élastique avant d’utiliser une loi non-linéaire ;
-
faire un calcul sans contact avant de le mettre en œuvre, faire un calcul avec frottement nul avant d’inclure le frottement, …
Toutes les étapes doivent être vérifiées proprement et il est nécessaire de vérifier que la solution converge lorsqu’on raffine le maillage et le pas de temps.
Enfin, il faut avoir à l’esprit que, dans les cas non-linéaires, il est possible que le problème à résoudre ne possède pas une solution unique (instabilité, bifurcation, etc.).
1) Choix de la discrétisation
La discrétisation doit être choisie avec soin de manière à être cohérente avec les chargements que l’on souhaite appliquer, notamment si ceux-ci ne sont pas monotones.
Plus les non-linéarités sont importantes, plus il faut utiliser des incréments de chargement petits. De même, si le modèle de comportement est complexe, il arrive que l’intégration de la loi de comportement ne soit pas totalement implicite : dans ce cas, il faut vraiment vérifier que les incréments sont suffisamment petits pour que le modèle ait convergé.
Selon les codes de calcul, une gestion plus ou moins automatique de ces pas de temps peut être proposée qui peut permettre de diminuer le pas de temps en cas de problème de convergence voire de l’augmenter si les non-linéarités sont faibles et que la convergence est très rapide. En toute rigueur, il convient de vérifier que la convergence en temps est bien atteinte en effectuant un deuxième calcul en diminuant les incréments de chargement.
2) Choix des conditions aux limites
Il faut avoir conscience que, dans le cas d’une loi de comportement de type adoucissante ou s’il existe une charge limite, le chargement à force imposée peut devenir illicite, comme illustré sur la figure ci-dessous.
Dans le premier cas, plus la force imposée s’approche de la charge limite, plus la convergence sera difficile, jusqu’à être impossible, si l’on cherche à la dépasser. Et dans le deuxième cas, il sera impossible de dépasser l’effort au pic et d’obtenir la solution post-pic.


Exemples de réponse avec charge limite ou perte de rigidité
Il existe également d’autres cas, où il n’existe pas une solution unique à effort donné ou déplacement donné. C’est le cas, par exemple dans le cas de flambement de coque mince ou lorsque le problème est tel qu’il existe des bifurcations, par exemple une branche dissipative et une branche élastique (cf. figure ci-dessous).


Réponse (a) avec branches multiples (b) non-monotone en déplacement et chargement
Si la modélisation correcte nécessite d’appliquer une force imposée, le problème peut être résolu via des méthodes de continuation ou de longueur d’arc (cf. documentation Code_Aster [R5.03.80] par exemple).
Pour qu’un code de calcul puisse travailler efficacement, il est donc nécessaire de concevoir son modèle, et de préparer les données, de telle façon qu’on travaille à la recherche d’une solution unique, en introduisant diverses restrictions, comme :
-
l’exigence d’un équilibre stable (en un sens à préciser !),
-
équilibre avec une condition de « moindre énergie de déformation plastique »,
-
équilibre avec une condition de « moindre courbure moyenne »,
-
équilibre avec une condition de « moindre contraste entre les réactions d’appui » …
3) Évaluation de la convergence de l'algorithme global non-linéaire
Les critères d’arrêt pour l’algorithme de Newton sont à considérer avec attention. Il convient de vérifier avec soin quel critère d’arrêt est programmé par défaut ou proposé par le logiciel utilisé. Par exemple, certains algorithmes vont tester la convergence sur la norme du résidu (dans ce cas, le critère dépend de l’unité de force utilisée dans le calcul, la précision n’est pas la même si le résidu requis est 1N ou 1MN), d’autres proposeront un critère d’arrêt où la norme du résidu est rapporté à la norme du chargement (dans ce cas, on s’affranchit de l’unité physique choisie). Des précautions toutes particulières doivent être prises dans les cas où on mélange différentes modélisations (massifs, éléments de structures) ou lorsqu’on utilise des éléments mixtes.
De manière générale, il faut faire très attention lorsqu’on dégrade le critère de convergence par rapport à la valeur recommandée pour aboutir à un résultat.
$translationBooksC.4 Problèmes de convergence ? Symptômes et solutions
C.4 Problèmes de convergence ? Symptômes et solutions
À la différence des calculs d’élasticité linéaire, les calculs non-linéaires peuvent effectuer des itérations apparemment indéfiniment, sans jamais vérifier le critère d’arrêt ; mais ils peuvent aussi s’interrompre brutalement à un incrément de chargement donné (au-delà du premier), avec signalement d’un « pivot nul ».
Examinons les causes de ces types d’échec.
1) Non-convergence des itérations
Ce phénomène est presque toujours une conséquence directe de l’inadéquation de la méthode itérative utilisée : le problème à résoudre ne vérifie certainement pas les conditions mathématiques qui assurent sa convergence (opérateur non-contractant, opérateur non-positif, opérateur non convexe, restrictions insuffisantes de l’intervalle dans lequel on recherche la solution, etc.).
Il peut arriver, il est vrai, que ce phénomène résulte d’une accumulation d’erreurs d’arrondis numériques, imputables à la programmation elle-même du code de calcul ; ce n’est toutefois pas souvent le cas.
L’examen des résidus au fil des itérations peut renseigner sur la nature du problème :
-
les résidus tendent bien vers 0, mais de plus en plus lentement. Ce comportement traduit un maillage inadapté au calcul de l’équilibre : c’est le cas dans les phénomènes de localisation, où les non-linéarités se concentrent dans certaines parties de la structure. Dans ce cas, il vaut mieux reprendre le calcul en réfléchissant à un maillage mieux adapté au mécanisme de la structure.
-
les résidus deviennent de plus en plus grands. C’est l’instabilité caractéristique : il n’existe plus, pour cette structure, d’état d’équilibre à ce niveau de chargement.
Les résidus, à partir d’un certain stade, remontent brutalement à une certaine valeur, puis reprennent leur décroissance, etc. Ce comportement survient lorsque l’algorithme tombe sur plusieurs solutions également viables sans autre précision : il converge vers l’une de ces solutions, puis « rebondit » vers une autre. Autrement dit, sans que l’on en ait conscience, il existe plusieurs équilibres possibles !
2) Arrêt brutal
L’arrêt brutal du programme dans un calcul non-linéaire se signale souvent par un « pivot nul » lors de la résolution d’un système linéaire. Cette expression renvoie au « pivot de Gauss », qui est l’algorithme utilisé (aux variantes près) pour résoudre les systèmes linéaires. On a vu plus haut, en effet, que la plupart des algorithmes itératifs remplacent le problème à résoudre par un système linéaire.
Cette situation correspond à une structure devenue instable : en élastoplasticité ou en endommagement, cela signifie que la structure a perdu toute cohésion, aux arrondis de calcul près ; dans les problèmes de grands déplacements ou de contact, cela traduit l’apparition d’un mécanisme, c’est-à-dire la possibilité d’un mouvement de corps rigide : tous les nœuds d’interface sont glissants, et les appuis fixes sont en nombre insuffisant pour obtenir un équilibre.
Il arrive aussi que le programme s’interrompe pour des raisons n’ayant aucun rapport avec l’état de la structure : débordement d’espace-disque, voire bug de programmation. Le premier cas est simple à écarter.
3) Quand rien ne marche
Si un calcul non-linéaire ne converge pas, et que l’on n’a pas trouvé dans les explications ci-dessus d’indications utiles, il y a lieu de passer attentivement en revue les questions suivantes :
-
l’état initial de votre calcul est-il bien un état d’équilibre élastique ?
-
le maillage est-il adapté à la question posée ? Le pas de maillage est-il suffisamment fin dans les zones où les déformations plastiques se localisent ? Les mailles ne sont-elles pas trop déformées ?
-
votre modèle mélange-t-il des éléments massifs et des éléments de structure (poutres, plaques, voire coques) ? Les zones plastifiées / endommagées de la structure affectent-t-elle des nœuds communs à ces éléments de type RdM ?
-
les éléments finis sont-ils adaptés au problème ? N’y a-t-il pas d’oscillations des contraintes ?
Chapitre D - Génie civil
Chapitre D - Génie civil
D.1 Les matériaux du génie civil
D.1 Les matériaux du génie civil
D.2 Les catégories d'éléments d'ouvrage
D.2 Les catégories d'éléments d'ouvrage
D.3 Les phases de construction
D.3 Les phases de construction
$translationBooksD.1 Les matériaux du génie civil
D.1 Les matériaux du génie civil
Ce chapitre a pour objectif de présenter les particularités de ces matériaux dans la perspective d'une modélisation aux éléments finis. Parmi celles-ci, nous trouvons les principaux matériaux utilisés en génie civil (béton, bois, métal) en eux-mêmes mais aussi leur utilisation dans des structures.
1) Béton
Le béton est un matériau composite composé de granulats de diverses tailles et d’une pâte. Cette pâte constituée de ciment, d’eau et le plus souvent d'adjuvants, joue le rôle d’une colle (liant) entre les granulats. Le béton bien qu’hétérogène a su révolutionner le monde de la construction grâce à ses propriétés telles que sa souplesse d’emploi, sa moulabilité offrant une variété d’aspects (forme, teinte, texture), sa résistance mécanique, sa résistance au feu, son isolation acoustique et sa diversité (béton armé, béton précontraint, etc.).
Cependant, le béton est soumis à des processus de dégradation. Ces derniers peuvent être issus de sollicitations environnementales telles que l’humidité, la pluie, le froid, le gel-dégel, la chaleur, le vent, la sécheresse, d’agressions provenant de sels de déverglaçage, d’alcali-réaction, de réactions sulfatiques interne et externe ou/et de corrosion et de sollicitations mécaniques comme des chocs, l’augmentation de la charge. Selon le phénomène de dégradation, la détérioration de l’élément structurel est progressive, une fois la contrainte de traction du béton atteinte. Cette dégradation conduit à la coalescence de microfissures vers la formation de macrofissures et la localisation des déformations. L’augmentation de la déformation entraîne la chute de la capacité résistante du matériau ce qui montre un comportement adoucissant ou de softening qui se termine par la ruine de la structure.
Loi de comportement - Dans les calculs par éléments finis, on ne considère généralement que certains aspects du comportement du béton car, c’est un matériau complexe. Pour que la loi de comportement du béton soit la plus pertinente, il est nécessaire de bien comprendre le comportement et les propriétés du béton. De ce fait, non seulement il est essentiel de connaître non seulement le comportement de la pâte de ciment, mais aussi les granulats, qui donnent au béton ses propriétés de rigidité et de raideur. Elle est responsable des propriétés de résistance mécanique du béton. Grâce à l’eau contenue dans la pâte, elle est également la cause de ses principales défaillances telles que l’augmentation de la porosité, la diminution de la résistance mécanique, les effets différés (retrait, fluage) et le transfert d’agents agressifs.
Le béton est considéré comme un matériau quasi-fragile de par son comportement complexe. Les principales caractéristiques de comportement sont mises en évidence dans la littérature. La caractéristique la plus significative propre au béton est son caractère fragile en traction et plus ductile en compression et sujet aux phénomènes unilatéraux lors de cycles traction/compression. D’autres aspects sont à prendre en compte tels que les déformations permanentes et les effets hystérétiques liés aux frottements entre les lèvres des fissures lors de chargements cycliques. Certaines propriétés sont à considérer également comme le retrait et le fluage selon l’environnement et le chargement appliqué au matériau béton.
Dans la littérature, les deux principales approches pour modéliser le comportement du béton sont :
-
Les modèles basés sur une approche continue. Cela veut dire que le béton est considéré comme un milieu continu (Bazant, 1979). Et pour tenir compte de la fissuration du béton, cette dernière est déduite de relations entre les déformations et les contraintes. Il existe les modèles élasto-plastiques (Ottosen, Drucker-Prager), endommageables (Mazars, Laborderie), à fissuration diffuse (smeared crack model), de type gradient et de type énergétique (fictitious crack model (Hillerborg, 1984), crack band model). Dans certains cas, des modèles élasto-plastiques sont utilisés mais l’utilisateur de ce type de loi doit être très prudent une fois la phase élastique dépassée car il est possible d’obtenir des déformations qui ne reflètent pas du tout le comportement du béton.
-
Les modèles basés sur une approche discrète. En effet, la fissuration du béton engendre des discontinuités géométriques, et ces discontinuités sont intégrées entre les frontières des éléments connectés. Il existe les modèles discrets de Ngo, (Ngo, 1967), Bazant (Bazant, 1979), Blaauwendraad (Blaauwendraad, 1981), les modèles à éléments finis enrichis (E-FEM, X-FEM), (Belytschko, 1999) et également les modèles de type lattice.
Mais dans la littérature, les deux catégories de modèles les plus utilisées sont les modèles basés sur la mécanique de l'endommagement et les modèles considérant la présence de discontinuité explicitement.
Bien que la composante élastique ne soit pas exactement linéaire ([Baron] p.276 ; [Sargin 1971]), on effectue le plus souvent les calculs en adoptant l’élasticité linéaire isotrope (loi de Hooke) pour représenter la phase élastique du comportement du matériau béton. On adopte pour le module d’Young et le coefficient de Poisson des valeurs obtenues après caractérisation du béton. Dans le cas où il n’est pas possible de faire d’autres caractérisations mécaniques sur le matériau béton pour déterminer ses propriétés mécaniques actuelles, certaines de ses propriétés comme la résistance en compression peuvent être déduite à partir de lois-modèles que l’on trouve dans des codes-modèles comme l’Eurocode 2, par exemple.
Note - Les bureaux d’étude ne s’écartent de ce modèle que pour des études de détail, sur une partie de la structure, où des phénomènes mécaniques particuliers se sont manifestés : fissuration, réaction de gonflement, hétérogénéité locale. Il existe en effet des éléments finis de type « élément fissuré », des modèles d’endommagement, des lois viscoplastiques ou enfin des lois couplées poro-mécaniques ; mais il faut disposer, pour de telles études, de données issues de l’auscultation de l’ouvrage ou de prélèvements de béton pour s’orienter vers ces lois de comportement particulières, pour lesquelles il faudra de toute façon fixer plusieurs coefficients ou modules dans la préparation du calcul.
Modèle élastoplastique – De manière simplifiée, le béton est souvent modélisé comme un matériau élastoplastique homogène et isotrope, ce qui est, bien sûr acceptable tant que le béton ne fissure pas.
Vis-à-vis d’une loi élastoplastique, la fissuration du béton n’est pas directement modélisée : les zones de fissuration sont caractérisées par des déformations anélastiques importantes (>1-2‰) et un état de contrainte figé entre la résistance en traction ft et la résistance en compression fc du béton.
Comme on l’a vu au chapitre 3, une loi de comportement élastoplastique est composée d’une loi élastique et d’une loi d’écoulement plastique, associée à un « critère de plasticité ».
Le comportement post-fissuration peut néanmoins être représenté de façon approchée par une courbe σ-ε descendante au-delà de la résistance en traction. Celle-ci peut couvrir les effets de tension softening (représentant le travail nécessaire pour ouvrir la fissure) et les effets de tension stiffening (contribution du béton entre les fissures, contraint par l’adhérence à l’armature).
Si le comportement décroissant matériel conduit à un comportement décroissant global, il faut prêter attention à d’éventuels effets de localisation : la taille des éléments finis va limiter la taille des zones anélastiques et la solution va dépendre du maillage utilisé. Différentes techniques numériques permettent de résoudre ou limiter ce problème.
Endommagement - Une loi d’endommagement est une loi qui rend compte d’un des principaux effets macroscopiques de la fissuration du béton : la perte de raideur du matériau. L’idée fondamentale est de renoncer à suivre individuellement les fissures (leur apparition et leur propagation), et de considérer que le béton d’une structure périt plutôt par multiplication de fissures dans les zones dégradées. Ce type de loi permet donc de décrire la diminution de la rigidité du matériau sous l’effet de la création de micro-fissures dans le béton. Cette perte de rigidité est mesurée par une variable interne appelée endommagement, notée D, qui évolue de 0 (matériau sain) à 1 (matériau totalement endommagé) ; cette variable est généralement scalaire.
Afin de représenter au mieux le comportement du béton, les lois d’endommagement tiennent compte du comportement post-pic adoucissant. Cela permet de déterminer la contrainte de la manière suivante :
 avec
avec 
Le mérite de cette approche est de considérer le béton comme un « milieu continu », cadre auquel la méthode des éléments finis est parfaitement adaptée.
Dans le cadre du comportement du béton, les deux principales familles de modèles d’endommagement sont les modèles anisotropes et isotropes. L'isotropie caractérise l’invariance des propriétés physiques du béton quelle que soit la direction. Alors que l’anisotropie est dépendante de la direction. Une loi anisotrope présente des réponses différences dues au chargement selon son orientation.
Un des modèles d’endommagement les plus utilisés dans le monde industriel et de la recherche est le modèle de Mazars [Mazars, 1984]. C’est certainement le premier modèle d’endommagement du béton fonctionnant de manière correcte.
Les principales difficultés posées par les modèles d’endommagement sont :
-
une dépendance a priori des résultats au maillage : il convient en principe de démontrer que le mécanisme de ruine obtenu par ce type de modèle est indépendant de la finesse de maillage, au moins à partir d’un certain seuil. C’est d’ailleurs cette dépendance qui a amené au développement de méthodes de régularisation.
-
l’absence de solution analytique dans des cas même simples.
Plusieurs classes de régularisation existent dont la régularisation non locale et la régularisation par l’énergie de fissuration [Hillerborg, 1976] (qui ne résout que partiellement le problème). Parmi les méthodes non locales, il est possible de citer les méthodes intégrales [Pijaudier et al., 1987], [Giry et al., 2011] ou les méthodes à gradient (gradient de déformations ou gradients de variables internes [De Borst et al., 1992], [Peerlings et al., 1996], [Nedjar, 2005], [Lorentz2017]. Ces méthodes nécessitent d’utiliser des maillages relativement fins ce qui les rend généralement très coûteuses en temps de calculs.
Effets différés et redistribution des contraintes - Dans l’étude du comportement d’un ouvrage en béton sur les semaines suivant le coulage du béton, mais surtout sur le long terme, il est nécessaire de tenir compte des effets différés tels que le retrait et le fluage.
Ces phénomènes propres au béton peuvent, en principe, être modélisés en adoptant une loi de comportement visco-élastoplastique (loi de Bingham), ou parfois même seulement viscoélastique (fluage « scientifique », [Eymard]) : cette approche est généralement mise en œuvre par les laboratoires de recherche, pour analyser les essais sur le matériau. Mais, dans le cas d’une modélisation plus fine tenant de ces effets différés, il est nécessaire d’intégrer des phénomènes tels que le séchage et la fissuration en plus du retrait et du fluage. Car tous ces phénomènes interagissent entre eux, d’où leur importance dans une modélisation numérique.
La déformation engendrée par le retrait est une déformation induite par le séchage du béton provenant des effets de l’environnement. Ce retrait induit une déformation différentielle du béton autrement dit des contraintes plus élevées aux zones à fort séchage. Ce phénomène engendre des contraintes de traction en surface entraînant la fissuration et des contraintes de compression en cœur.
Concernant le fluage, sa déformation est généralement décomposée en deux déformations, l’une due au fluage propre et l’autre au fluage de dessiccation. Cela vient du fait que le fluage dépend fondamentalement de l’humidité relative.
Dans l’Eurocode 2, il est possible de déterminer la déformation du béton due aux effets différés (sans chargement extérieur). Pour ce faire, il faut calculer la déformation du au retrait endogène (conséquence de l’humidité interne) et la déformation de dessiccation (conséquence du séchage et de la taille de l’élément structurel). Et la déformation de fluage sous contrainte de compression σc est égale, selon le §3.1.9 de l’EN1992-1-1 à :

où Ec est le module tangent (égal à 1,05 Ecm) et φ est le coefficient de fluage.
L’Eurocode 2 (EN1992-1-1) donne une méthode simplifiée de calcul de φ(∞,t0). L'annexe B donne une méthode plus complète permettant d'estimer φ(t,t0) ainsi que l'évolution du retrait (voir également l'annexe B de l'EN1922-2). De plus, il est important de retenir que le calcul des déformations différées fait intervenir le type de ciment.
2) Acier de charpente
Le comportement de l’acier est beaucoup plus simple que celui du béton, et cela pour plusieurs raisons : c’est un matériau isotrope, présentant des résistances et des modules identiques en traction et en compression. De plus, il fait l’objet de contrôles industriels qui assurent son homogénéité.
Modèles élastiques - Bien que l’acier se comporte essentiellement comme un matériau élastoplastique isotrope (Eurocode 3, partie 1.1, §5.4.3), les modélisations usuelles des structures acier, ou composites comportant de l’acier, adoptent pour ce dernier un comportement élastique linéaire. L’on vérifie a posteriori que la contrainte dans l’acier est inférieure à la limite élastique fy. Dans le cas d’éléments de type poutre ou poteau, les normes autorisent, si les sections présentent des dimensions assurant une ductilité locale suffisante, à dépasser dans l’analyse la résistance élastique et à considérer des moments résistants basés sur une distribution plastique des contraintes.
Élastoplasticité et écrouissage - La théorie de l’élastoplasticité s’est en fait développée à partir de l’étude des alliages acier, notamment en vue de prédire les efforts de laminage et de forgeage ([Hill], [Nadai]). Pour l’acier, le modèle usuel se compose de la loi de Hooke pour la déformation élastique, et du critère de plasticité dit « critère de von Mises », comme y invite d’ailleurs l’Eurocode 3 (partie 2, § 7.3 ; partie 1.5 §10 et partie 1.7 §5.2.3.2) : pour ce critère, il suffit de donner la contrainte de limite élastique fy de l’acier.
Du point de vue du calcul par éléments finis, il se pose encore la question de la prise en compte de l’écrouissage du matériau, c’est-à-dire de son durcissement dans la phase purement plastique. Cet aspect est notamment abordé à l’annexe C6, partie 1.5 de l’Eurocode 3. Dans un souci de vérification du modèle, il est sans doute préférable d’effectuer un premier calcul avec un modèle sans écrouissage : en effet, on peut alors vérifier la qualité des contraintes obtenues dans les zones plastiques en affichant les isovaleurs de la contrainte de von Mises (les zones plastifiées doivent être à peu près monochromes). Il est cependant à noter que l’usage d’une loi élastique parfaitement plastique, sans écrouissage, peut entraîner des problèmes de convergence de l’analyse non linéaire. En effet, les zones plastifiées présentent un module tangent nul et n’ont donc pas de raideur. La prise en compte de l’écrouissage permet de stabiliser la résolution numérique.
En cas d’écrouissage jusqu’à une contrainte de valeur fy+X, les décharges et recharges éventuelles se font élastiquement, avec un module égal au module initial. fy+X devient donc la limite d’élasticité apparente du matériau. Par ailleurs, le comportement de l’acier est proche du modèle d’écrouissage cinématique. En première approche, l’on peut considérer qu’un écrouissage en traction jusqu’à une contrainte (fy+X) entraîne une diminution de la limite d’élasticité en compression à la valeur fy-X, et vice versa.
Le modèle le plus courant pour l’acier est cependant l’écrouissage isotrope, dépendant de la déformation plastique cumulée :

Dans ce cas, il n’y a plus de distinction entre traction et compression et un écrouissage dans un sens de sollicitation entraîne une augmentation de la limite d’élasticité en compression. Cette hypothèse n’est donc valable que si le chargement considéré est monotone, et non cyclique.
Dans presque tous les codes de calcul, on peut afficher les isovaleurs de la déformation plastique cumulée : ainsi, il est possible de vérifier, dans les zones plastiques, que la contrainte de von Mises se répartit conformément à cette déformation.
Dans le cas particulier de l’acier inoxydable, l’hypothèse d’un comportement linéaire jusqu’à la limite d’élasticité conventionnelle fy, correspondant à une déformation plastique de 0,2 %, n’est pas respectée, et, comme le précise l’Eurocode 3-1-4, §4.2., il convient de prendre en compte les effets du comportement non linéaire en contrainte-déformation dans le calcul des flèches. La loi matérielle est de type Ramberg-Osgood, et des indications pour sa modélisation sont données par l’annexe C de cette partie de l’Eurocode.
3) Acier de précontrainte
Du point de vue du comportement, les aciers de câbles (haubans, suspentes) et les aciers de précontrainte ne diffèrent des aciers de charpente que par une limite élastique environ trois fois plus élevée (de 1680 à 2140 MPa en France), justifiée d’ailleurs par des sollicitations en service généralement supérieures à 1000 MPa. On peut donc, en première intention, modéliser les armatures de précontrainte comme des éléments à comportement élastique linéaire, ou à comportement élasto-plastique de type von Mises.
Les aciers de précontrainte sont tous laminés à chaud, et il y a donc lieu, en phase plastique, de prendre en considération une loi d’écrouissage linéaire isotrope. Le coefficient d’écrouissage h peut être calculé à partir des caractéristiques garanties par l’armaturier :

où Rm est la contrainte à rupture, fp0,1 la limite conventionnelle d’élasticité, E le module d’Young et Agt l’allongement à rupture.
Une conséquence directe de ce niveau de contrainte élevé est l’amorçage de mécanismes de relaxation. La relaxation des aciers est un effet différé (dépendant essentiellement du temps écoulé depuis le chargement), donc non-élastique. Elle se traduit, pour une barre ou un câble soumis à un allongement constant, par une baisse progressive de la contrainte. Ce mécanisme ne s’amorce, à la température ambiante, que pour un allongement dépassant environ 60 % de la limite élastique (soit environ 1000 MPa). La relaxation augmente sensiblement avec la température.
Comme pour le fluage des bétons, on peut modéliser la relaxation avec une loi de comportement visco-élastique linéaire ; toutefois, cette approche est plutôt réservée aux travaux de recherche. En règle générale, il n’est pas courant de modéliser les aciers de précontrainte : on se borne souvent à introduire l’action de la précontrainte par une distribution de forces réparties à travers les éléments en béton. Cependant, pour des analyses de détail, où l’on s’intéresse à l’interaction entre les câbles et le coulis d’enrobage, on peut prendre en compte la relaxation par un calcul incrémental en temps, où les pertes de relaxation sont introduites comme des contraintes initiales.
4) Acier passif
Action mécanique normale des aciers passifs - Dans les calculs par éléments finis, les aciers passifs sont fréquemment modélisés par des éléments linéaires, c’est-à-dire unidimensionnels, de type « barre ». Suivant les principes des règlements de béton armé historiques, on considère en effet que les armatures agissent principalement en reprenant les tensions et compressions du béton suivant leur axe propre, et c’est précisément ce que permet le modèle d’élément fini de barre. L’accrochage aux nœuds des éléments massifs représentant le béton permet, au demeurant, d’éviter les mécanismes propres aux assemblages de barres seules.
Dans la plupart des codes de calcul, les éléments de barre sont considérés, par défaut, comme des éléments à comportement élastique linéaire. Étant donné le caractère unidimensionnel de ces éléments, on a donc une loi du type N = E A u/L, où u est le déplacement axial, et N l’effort normal aux nœuds. Il faut vérifier a posteriori que la contrainte axiale N/A reste comprise entre ±fy.
Adhérence - Ce qui précède ne vaut, bien sûr, qu’à la condition qu’il y ait adhérence continue entre les armatures passives et le béton.
5) Bois
Le bois est un matériau qui présente quelques singularités : il n'est pas homogène et ceci à différentes échelles, il n'est pas isotrope, il ne présente pas de comportement symétrique, il peut présenter des ruptures ductiles ou fragiles selon la sollicitation et son orientation. Le bois est sensible à l'humidité, ce qui a un impact sur ses caractéristiques dimensionnelles et sur sa raideur et sa résistance. La durée de chargement a un impact important sur la résistance et la déformée des éléments en bois ; les variations d'humidité peuvent accélérer ces déformées (mécanosorption). Sur la base de ce constat, on peut asseoir un raisonnement pour aborder une modélisation par la méthode des éléments finis.
Homogénéisation - L'hypothèse doit être validée sur le volume élémentaire représentatif, a minima, le volume du plus petit élément fini. En sachant que, selon les essences, les cernes de croissance peuvent dépasser 1 cm, il deviendra problématique d'assumer cette hypothèse d'homogénéisation à proximité des organes d'assemblages (pointes, broches, boulons…) qui présentent un diamètre de cet ordre de grandeur, voire plus faible.
La présence de nœuds est rarement prise en compte dans les modélisations de structure ou d'éléments de structure.
Orthotropie - Le bois présente une structure et des caractéristiques fonction de trois directions, la direction longitudinale – l'axe du tronc – le fil du bois, les directions radiales et tangentielles, perpendiculaires à la direction longitudinale. Ces dernières s'inscrivent dans un plan, souvent celui des sections droites de poutres, sur lequel apparaît plus ou moins nettement les cernes de croissance. Le repère d'orthotropie est donc un repère quasi cylindrique, alors que le repère des éléments s'inscrit plutôt dans un référentiel cartésien. La représentation de cette orthotropie, quand elle est prise en compte, se limite dans la grande majorité des cas à une hypothèse d'isotropie transverse (axes radial et tangentiel à caractéristiques identiques) dans un référentiel cartésien. La pente de fil associée à la présence de nœuds n'est en général pas prise en compte dans le calcul des éléments. Par contre, elle est modélisée dans le calcul des assemblages, notamment pour les assemblages par contact.
La matrice de souplesse (inverse de la matrice de rigidité) peut être définie comme suit pour un cas plan orthotrope :

Remarque : L’hypothèse d’orthotropie et de symétrie de Sij réduit le nombre de termes indépendants de 36 (cas 3D le plus général) à 9 termes.

Bois – hypothèse orthotrope
Modélisation élastique - Il suffit de disposer de la matrice de comportement isotrope transverse pour une modélisation 2D ou 3D. Les modules entre les directions longitudinale et radiale ou tangentielles peuvent présenter des rapports de l'ordre de 20. Ils évoluent en fonctions de la durée de chargement (fluage), de l'humidité du bois à la mise en œuvre et de son évolution dans le temps (environnement). La représentativité du résultat MEF dépendra de la pertinence des paramètres pris en compte.
Modélisation plastique, critères de rupture - Pour une matériau isotrope transverse non symétrique, on peut s'orienter vers des critères de Hill, de Tsai… en sachant qu'il sera nécessaire de décrire la rupture fragile, en traction perpendiculaire et en cisaillement. La grande variabilité des résistances rend le calage des paramètres des critères délicat. La succession de cernes de croissance, ou celle des lamelles assemblées, avec des caractéristiques mécaniques différentes, peut rendre un modèle homogène difficile à caler en termes de résistance. En effet, la résistance et la rigidité sont fortement corrélées pour le bois et des effets « système » apparaissent rapidement en termes de résistance d'élément. Ainsi, on dispose de limites de résistance en traction longitudinale, en compression longitudinale, en flexion…
Enfin, les structures en bois sont particulièrement sensibles au comportement de leurs assemblages. Ceci peut présenter l'avantage de ne pas avoir à modéliser finement les éléments, mais à s'intéresser plus précisément aux zones d'assemblages. Par contre, apparaissent les problématiques de contacts, de matériaux multiples, de la plastification de certains, de rupture fragile d'autres, des limites d'homogénéisation rappelées précédemment.
Il apparaît clairement que l'effort de modélisation est lié à l'échelle d'investigation, ou au stade du projet. Sous réserve de prise en compte des singularités listées ici, la modélisation du bois au sein d'une structure peut être menée comme pour un autre matériau.
Modélisation des effets différés et de l’interaction avec les phénomènes hydriques - Le bois est un matériau hygroscopique sensible au changement d’humidité relative de l’air. Il est par ailleurs sujet à des effets de fluage sous contrainte. Si l’on désire modéliser ces phénomènes, l’on peut adopter un modèle de type viscoélastique vieillissant en environnement variable, en accord avec les principes de la thermodynamique. Le modèle de comportement viscoélastique de type Kelvin-Voigt généralisé, caractérisé par des paramètres rhéologiques vieillissants et dépendant du niveau et de l’histoire de l’humidité peut être associé au modèle de comportement non-viscoélastique de Ranta-Maunus pour caractériser le retrait-gonflement et la mécano-sorption.
$translationBooksD.2 Les catégories d'éléments d'ouvrage
D.2 Les catégories d'éléments d'ouvrage
On présente ici les particularités de ces éléments eu égard à un calcul aux éléments finis.
1) Éléments de Béton Armé
Prise en compte des phénomènes différés - Le plus souvent, l’ingénieur de projet s’intéresse aux effets de redistribution des contraintes et aux déformations différées qui accompagnent le vieillissement des matériaux.
Pour y parvenir, le calcul statique par incréments de temps est particulièrement bien adapté et largement suffisant. Le retrait et le fluage du béton, par exemple, ne dépendent que du temps écoulé depuis le remplissage du coffrage. Dans un calcul incrémental, ils seront introduits comme des déformations imposées en chaque nœud du maillage. Il est possible de calculer a priori, pour chaque pas de temps ou incrément, la carte des déformations de retrait et de fluage : le solveur éléments finis intègre cet état initial dans la recherche de l’équilibre d’un matériau élastoplastique.
Il convient néanmoins de prêter attention à l’interaction entre les effets différés et les phases de construction, comme cela sera expliqué par la suite.
Prise en compte de la fissuration - Lorsque le béton se fissure en traction, il se développe des fissures débouchant vers le parement le plus proche, ainsi que des fissures le long de l’interface acier béton ([Goto], figure ci-dessous).

Fissuration interne du béton armé
Lorsque l’on considère une bielle tendue de béton armé fissuré comme un milieu continu homogénéisé, la loi de comportement N(ε) (où N est l’effort normal de traction) suit l’allure de la figure ci-dessous.

Modèle schématique de l'effet de tension stiffening
Le Model Code 1990 de la CEB-FIP en donne une expression analytique. Cette relation peut être utilisée en modélisant la section de béton fissurée comme un élément de barre dont on actualiserait le module de rigidité par incréments (suivant la valeur de l’effort normal ou de l’allongement, puisque la relation est inversible). On peut aussi l’utiliser comme loi de comportement d’une fibre d’un élément multifibre.
Béton confiné - Pour les zones de béton confinées (par des cadres d’armature passives, par exemple), il est possible de prendre en compte la résistance résiduelle post-écrasement, comme l’indique l’EN1992-1, en utilisant la loi de Sargin :

 avec εc1 la valeur au pic telle que
avec εc1 la valeur au pic telle que 
 avec
avec 
Pour 
L’EN1992-1 au §3.1.9 propose également un incrément de résistance et de déformation du béton quand il est soumis à un contrainte de confinement de valeur σ2=σ3 tel que :



Cette loi n’est toutefois qu’unidimensionnelle, et ne vaut que sous chargement monotone. On ne peut donc s’en servir avec la méthode des éléments finis qu’en modélisant le béton confiné par un élément de barre (donc on modifierait incrémentalement le module), ou comme loi de comportement d’une fibre d’un élément de poutre multi fibres.
2) Éléments en Béton Précontraint en Pré-tension
La précontrainte par pré-tension, caractéristique notamment des produits en béton préfabriqués industriellement (poutres, prédalles, dalles alvéolées, poutrelles…), consiste à venir tendre des câbles (fils, torons ou barres) dans des bancs de fabrication puis de venir couler le béton avant de détendre les câbles lorsqu’une résistance minimale du béton est atteinte (appelée résistance du béton au relâchement). L’intensité de la tension des câbles (qui ne doit pas dépasser la force de précontrainte maximale autorisée par les codes de calculs), le nombre de câbles et la résistance du béton sont ajustés en fonction des charges que doit reprendre le plancher ou l’élément précontraint.
Lors de cette détention, des pertes instantanées, de l’ordre de 8% pour une prédalle précontrainte par exemple, doivent être prises en compte (pertes dues à la rentrée d’ancrage, à la relaxation des armatures de précontrainte pendant la période entre la mise en tension des armatures et le transfert de la précontrainte, au raccourcissement élastique du béton sous l’effort de compression imposé par la précontrainte) lors d’un dimensionnement en phase provisoire de chantier avec une longueur de transmission de la précontrainte à considérer en partant de l’about de l’élément préfabriqué en béton.
A plus long terme, des pertes différées dues au retrait du béton, à la relaxation de l’acier ou au fluage du béton pour atteindre au final une perte totale de 20 % par exemple pour une prédalle précontrainte, doivent également être considérées.
Dans de nombreux codes de calculs aux éléments finis, la précontrainte peut être intégrée dans des éléments finis de type poutre représentant les câbles liaisonnés à des éléments finis volumiques représentant le béton. Suivant la zone d’étude, il peut être nécessaire par exemple dans les zones d’abouts de considérer la longueur de transmission de la précontrainte dans les câbles. La distribution de la force réelle de précontrainte (avec prise en compte des pertes instantanées ou différées en fonction du moment dans la durée de vie du produit où l’on souhaite faire le calcul/vérification) est alors variable le long de cette longueur de transfert. Une distribution linéaire de cette force de précontrainte est autorisée dans la plupart des codes de calculs et reste dans la plupart des cas sécuritaire pour le dimensionnement par rapport à la distribution parabolique plus réaliste.
Pour des raisons de complexité et de besoin (dimensionnement limité à des déformations élastiques), la modélisation de ces éléments est réalisée la plupart du temps avec des hypothèses linéaires (lois de comportement du béton et de l’acier élastique linéaire, contact parfait entre le béton et l’acier…). Pour des études fines, des hypothèses non linéaires peuvent toutefois être mises en place selon le besoin comme par exemple des lois de comportement de type endommagement pour le béton, de type élasto-plastique pour l’acier et l’introduction d’éléments d’interface acier-béton.
3) Éléments en Béton Précontraint en Post-tension
Pertes élastiques - La mise en tension des câbles de précontrainte par post-tension s ’accompagne de pertes instantanées : frottement, recul d’ancrage et perte par allongement élastique.
Effets différés : fluage, retrait et relaxation - La prise en compte des effets différés s’effectue par un calcul incrémental. Le fluage et le retrait peuvent être introduits comme des déformations volumiques incrémentales, données en chaque nœud du maillage.
4) Éléments de charpente métallique
Choix du type d’analyse
De par leur fort élancement, les charpentes métalliques sont très déformables. Il en résulte que l’hypothèse traditionnelle de réaliser l’équilibre des efforts en configuration initiale n’est pas toujours valable ; il faut alors établir les distributions d’efforts internes en configuration déformée.
La sensibilité à ces effets non linéaires, dits parfois du second ordre, est jugée au travers du multiplicateur critique αcr, le multiplicateur des charges conduisant à l’instabilité eulérienne de la structure. Dans la version actuelle de l’Eurocode 3 :
-
si αcr > 10, les effets non linéaires peuvent être négligés. Si l’analyse structurelle globale intègre la plasticité des éléments, la valeur limite de αcr est augmentée jusqu’à 15 ;
-
si 4 < αcr < 10, ils doivent être pris en compte. Ceci peut cependant se faire par une analyse élastique linéaire classique, en amplifiant les efforts transversaux ;
-
si αcr < 4, l’analyse non linéaire est obligatoire.
Dans les deux derniers cas, les imperfections géométriques globales doivent être considérées, ainsi que les imperfections d’éléments si elles influent sur le comportement global.
Les imperfections d’éléments regroupent :
-
les imperfections géométriques : imperfections transversales et en torsion ;
-
les imperfections matérielles : les éléments laminés, ou reconstitués par soudage, présentent des distributions de contraintes résiduelles autoéquilibrées créées par leur processus de fabrication.
Ces dernières peuvent être représentées par une imperfection géométrique équivalente, dont la valeur peut être trouvée dans les normes en vigueur.
Ces imperfections doivent être intégrées pour toute analyse d’un élément de charpente intégrant les effets non linéaires.
Les modèles de type structure ou RdM (barres, poutres, plaques et coques) sont en principe idéalement adaptés aux calculs de charpente métallique.
Structures filaires
Analyse élastique
En vue de la modélisation, il y a lieu toutefois d’analyser précisément :
-
la nature des liaisons entre les différents éléments de charpente,
-
et le mode de transfert des charges de chaque pièce aux autres.
Analyse plastique
Lorsque la ductilité sectionnelle et/ou la ductilité des assemblages est assurée, il est possible de réaliser des analyses structurelles intégrant la plasticité. Différentes méthodes peuvent être utilisées (EC3, §5.4.3) :
-
analyse élastique-plastique, où les zones plastifiées sont modélisées comme des rotules plastiques ;
-
analyse plastique non linéaire, prenant en compte la plastification partielle des barres le long des zones plastiques ;
-
analyse rigide-plastique, dans laquelle le comportement élastique des barres entre les rotules est négligé.
Torsion
Les éléments en acier sont rarement massifs ; ils sont composés de parois minces pour constituer des profils, ouverts ou fermés. En particulier dans le premier cas, la réponse aux sollicitations en torsion se fait à la fois en torsion uniforme, dite de Saint Venant, et en torsion non uniforme, entraînant un gauchissement de la section. Ce dernier phénomène n’est habituellement pas pris en compte dans les logiciels commerciaux, alors qu’il peut avoir un effet déterminant dans la réponse des structures. Dans ce cas, deux solutions sont envisageables :
-
procéder à une modélisation surfacique de l’élément : cette solution est inapplicable si l’analyse porte sur une structure comportant plus de quelques éléments ;
-
si l’on est dans une situation similaire à celle de la poutre en I, où la torsion non uniforme peut se représenter par la flexion alternée des semelles (appelée biflexion, Figure), procéder à une modélisation bifilaire de l’élément : les deux semelles sont représentées par deux éléments distincts, reliés par des éléments transversaux représentant l’âme. De ce fait, la flexion spécifique de chaque semelle, et partant la torsion non uniforme, est représentée. Ce cas se présente notamment pour les ponts mixtes bipoutres. Une application est présentée au chapitre 3.

Décomposition de la torsion en torsion uniforme et non uniforme : hypothèse simplifiée de biflexion
Éléments bi ou tridimensionnels
L’analyse élastique linéaire des éléments aciers bi ou tridimensionnels ne présente pas de problèmes spécifiques, et les règles générales s’appliquent.
Par contre l’analyse non linéaire peut être requise pour étudier les phénomènes d’instabilité. En effet, les structures composées de plaques d’acier, qu’elles soient planes ou courbes, sont sujettes à des phénomènes de voilement.
Dans le cas des éléments plans, appelés plaques, le voilement est un phénomène relativement stable : l’initiation du voilement de la plaque n’entraine pas la ruine, la charge maximale est atteinte après voilement. On parle de comportement post-critique.
Dans le cas des éléments courbes (coques), l’instabilité entraine la ruine immédiate de la structure, souvent brutale. D’un point de vue numérique, dans une analyse statique non linéaire, cela se traduit par une rapide décroissance de la charge au-delà du maximum.
Dans les deux cas, la charge maximale est fortement dépendante de la déformée initiale appliquée, tant en amplitude qu’en forme. L’amplitude est fixée par les normes. La forme est choisie habituellement affine au premier mode d’instabilité. Cependant ce choix n’est pas nécessairement le plus pénalisant. Il est conseillé de le compléter par des modes locaux lorsque la structure présente des panneaux de dimensions fortement différentes.
Par exemple, dans le cas d’un platelage orthotrope, la déformée affine au mode de voilement global doit être complétée de déformées affines au voilement des sous panneaux.
Dans le cas des structures de type coque, le problème est encore plus critique. Il est conseillé, une fois un premier calcul effectué selon les hypothèses ci-dessus, d’adopter dans un deuxième calcul une forme de déformée initiale affine à la déformée obtenue à la ruine.
5) Structures mixtes : acier-béton
L’alternative d’une construction mixte acier-béton est parfois préférée pour certains types de bâtiments industriels et pour des ponts de petites à moyennes portées (travée centrale < 100 m). L’alliance de ces deux matériaux en les faisant « travailler » dans leurs domaines de résistance (béton en compression et acier en traction) permet d’obtenir une structure légère et résistante. Afin d’aboutir à ce résultat, la connexion entre ces deux matériaux se doit d’être correctement dimensionnée. On distingue :
-
les dalles mixtes : dalle pleine + bac collaborant,
-
les poutres mixtes : dalle pleine ou mixte + profilé métallique + connecteurs,
-
les poteaux mixtes : profilé métallique + (remplissage béton ou enrobage béton).
Les analyses structurelles globales sont usuellement menées par analyse élastique en homogénéisant la section, ou en représentant de façon séparée les deux matériaux. Cette deuxième façon de procéder peut conduire à des difficultés dans le traitement des résultats, puisqu’il faut recalculer les efforts sur la section globalisée pour pouvoir appliquer les règlements en vigueur.
Lorsque l’on désire effectuer des analyses plus fines, étant donné la diversité des matériaux mis en collaboration dans ce type d’alliance, autant sur le plan géométrique que sur le plan du comportement en général non-linéaire, des modèles aux éléments finis 3D s’avèrent nécessaires pour mener des études locales incluant un traitement des diverses interfaces (par des éléments finis de contact par exemple). Pour des études à l’échelle de la structure ou des éléments, des modèles 2D relativement performants ont été développés cette dernière décennie notamment, ceux basés sur un découpage de la section transversale en fibres (modèle à fibres) pour permettre d’estimer par intégration numérique la rigidité en section.
Le raboutage des poutres de ponts mixtes constitue aussi un détail relativement complexe. Quelle que soit la solution de raboutage retenue (par couvre-joints, par chevêtre ou par diaphragme), les modèles 3D utilisant des éléments finis de type massifs sont préférés aux modèles 2D simplifiés mais requièrent des temps de calculs relativement importants.
Fissuration - Les poutres mixtes sont usuellement constituées d’un profil métallique solidarisé à un plancher ou un tablier en béton armé au moyen de connecteurs. Il en résulte que, dans les zones de moment positif, où la dalle est comprimée, la résistance et la raideur sont particulièrement importants, alors que dans les zones de moment négatif, la fissuration entraîne des caractéristiques mécaniques nettement moindres. Ceci ne peut être négligé dans l’analyse structurelle globale de la structure. Différents niveaux de modélisation sont admis dans les codes :
-
Approches forfaitaires : par exemple, l’Eurocode 4 préconise de prendre une longueur fissurée égale à 15 % de la portée, de part et d’autre des appuis. Il propose aussi une raideur forfaitaire pour les poteaux mixtes. L'eurocode 8 quant à lui préconise d’adopter une raideur moyenne sur toute la longueur de la poutre. Ces différences d’approche se justifient par la forme différente des diagrammes de moments sous sollicitation classique majoritairement gravitaire, et sous sollicitation sismique ;
-
Approches définissant une zone de fissuration par analyse des sollicitations enveloppes : l’Eurocode 4 préconise de considérer comme fissurée toute section où la contrainte dépasse de deux fois la résistance en traction moyenne sous l’enveloppe des sollicitations caractéristiques calculées en supposant la structure non fissurée, en adoptant un module de béton à long terme
-
Il est aussi loisible de recourir à des analyses non linéaires.
Connexion
Sauf en cas d’analyse non linéaire, il n’est pas utile de modéliser la connexion. Les normes actuelles permettent de prendre en compte l’effet d’une connexion partielle sur la résistance des éléments.
Dans le cadre de la modélisation, des éléments finis de type poutre (2D ou 3D) sont en général utilisés pour modéliser la connexion ponctuelle. Pour une hypothèse de connexion répartie, il existe des modèles appropriés dans la littérature.
Largeurs collaborantes
Les poutres acier sont connectées à des éléments particulièrement larges et le trainage de cisaillement peut entraîner une répartition non uniforme des contraintes sur la largeur de la dalle.
Dans les modélisations filaires, ce phénomène est habituellement pris en compte en adoptant une largeur réduite de dalle dans la modélisation, à contrainte constante puisque la modélisation poutre l’impose.
En toute rigueur, comme le trainage de cisaillement est lié à la transmission de l’effort rasant par la connexion à la dalle, et est donc dépendant de la forme du diagramme de moment, la largeur collaborante devrait varier de combinaison à combinaison. Cependant les normes autorisent d’adopter une largeur unique pour l’ensemble des calculs.
Cette variabilité des largeurs collaborantes sera prise en compte si une modélisation de la dalle est réalisée par des éléments de type surfacique.
Effets différés et retrait
Les effets différés du béton influent sur la répartition des raideurs dans la structure et donc sur la répartition des efforts et doivent être pris en compte. Il est à noter que l’Eurocode module la valeur du coefficient d‘équivalence acier-béton en fonction du type de chargement. La sollicitation de retrait induit une distribution de contrainte autoéquilibrée sur la section ; celle-ci aussi doit être prise en compte.
Analyses non linéaires
La modélisation non linéaire des structures mixtes adopte les hypothèses matérielles et d’imperfections géométriques utilisées pour les matériaux béton et acier seul.
Comme déjà dit, la connexion doit être modélisée avec sa propre raideur. Il est à noter que son traitement numérique reste délicat : habituellement, il est supposé que les parties béton et acier ne peuvent se désolidariser transversalement, et que seul un glissement longitudinal est possible. La formulation éléments finis d’une telle liaison peut entraîner des phénomènes de « locking » : le glissement est bloqué par un jeu de projection de la raideur transversale empêchant le soulèvement lorsque l’équilibre est établi en configuration déformée. Il convient donc, lorsque ce type d’élément est utilisé, de vérifier la cohérence des efforts apparaissant dans la connexion avec les efforts de traction/compression des éléments acier.
6) Haubans, suspentes et câbles porteurs
Introduction dans les calculs - Certains éléments de câbles peuvent être modélisés comme des barres de section équivalente : tel est le cas des suspentes verticales, ou des câbles de précontraintes, guidés dans leur gaine : la courbure de ces câbles à l'équilibre est pratiquement indépendante de leur masse linéique. Dans les autres cas, le poids propre des câbles tend à la courber : la direction verticale est une direction particulière qui intervient dans la raideur de ces éléments.
Lorsqu’à l’échelle de la portée du câble, sa courbure devient importante, celle-ci conditionne fortement les contraintes et les efforts qu’il peut transmettre au reste de l’ouvrage. Pour les haubans, par exemple, la raideur du câble dépend principalement de sa flèche, et de son allongement. La flèche dégrade la raideur du câble, et donc la relation tension/flèche du câble est par essence non-linéaire.
Les éléments de câble présents dans la plupart des codes s’inspirent du modèle de [Gimsing], qui suppose que le câble se déforme selon une courbe parabolique, hypothèse qui est valide dès lors que le rapport flèche/portée est inférieur à 1/12 environ. Ce modèle découple l'allongement élastique de la flexion du câble.
Effet de chaînette - Lorsque la flèche d'un câble est supérieure à 1/12 de sa portée, il n'est plus possible de découpler l'allongement élastique de la flexion, car le bras de levier de la tension devient prépondérant dans l'expression du moment fléchissant. Plusieurs codes de calcul proposent des éléments de caténaire pour rendre compte de cet effet géométrique. Ces éléments connectent deux nœuds du maillage, et un seul élément suffit pour modéliser le câble.

Déplacements nodaux d'un élément de chaînette
Pour ce type d'élément, les inconnues nodales sont le déplacement vertical (dans la direction de la gravité) et le déplacement horizontal (cf. figure 4) ; les réactions associées sont la variation de la composante horizontale de la tension du câble, et la réaction verticale aux ancrages. La relation entre les déplacements nodaux et ces réactions dépendant de la tension du câble, la recherche de l'équilibre est un problème non-linéaire, quoique la structure soit globalement élastique.
$translationBooksD.3 Les phases de construction
D.3 Les phases de construction
Les études des phases de construction ont deux objectifs :
-
s’assurer de la stabilité de la structure dans les différents états transitoires conduisant à l’état définitif ;
-
calculer les effets du montage sur la distribution des efforts et sur la déformée de la structure en service.
Les effets du montage sont multiples. Ils sont liés :
-
à l’évolution du schéma statique en cours de construction. Par exemple, une travée de pont construite par deux encorbellements à partir de ses deux extrémités et finalement clavée en son centre présentera juste après le clavage un diagramme de moment sous charges permanentes qui s’annule en milieu de travée, bien différent de celui qui aurait été obtenu sans prise en compte du mode de montage (Figure 5) ;
-
à l’interaction des effets différés avec l’évolution du schéma statique. Dans l’exemple cité précédemment, après clavage, le moment en milieu de travée va croître sous l’effet du fluage ;
-
à l’évolution des sections au cours du temps. Par exemple, dans le cas des ouvrages mixtes acier-béton, le poids de la dalle est supporté par la structure métallique seule si la structure ne repose pas sur des cintres lors du coulage du béton;
-
à des réglages volontaires de la structure : dénivellations d’appui, réglages des haubans, vérinages en clef d’arc, …
La prise en compte de ces effets peut s’avérer relativement complexe et, dans les cas les plus difficiles, il peut être indispensable de recourir à un logiciel capable de modéliser pas à pas l’évolution de la structure.
Il est cependant souvent possible de procéder par une superposition de différentes analyses linéaires.

Effet des phases de construction : principe dans le cas du clavage d'une travée de pont construite en console
Les principales difficultés sont liées aux effets des déformations différées du béton. En effet, comment évaluer le moment à terme en milieu de travée, dans l’exemple présenté plus haut ? Dans le cas d’un clavage unique, il est possible d’utiliser la méthode dite « des coefficients » (Figure 6). Cette approche repose sur les points suivants :
Etat à terme = (E(t0, t1)/E(t0, t∞)) x Etat à terme non clavé + (1-(E(t0, t1)/E(t0, t∞))) x Etat à terme sans phasage
t0 étant le temps d’application de la charge, t1 le temps du clavage, t∞ le temps considéré pour l’état à terme, et E(t0, t1) le module de béton pour l’obtention de la déformation du béton au temps t1 pour une contrainte appliquée en t0.
Cette méthode, dans le cas d’un clavage unique, restitue l’état à terme théorique exact. Elle est cependant difficilement extensible au cas de clavages multiples, et peut conduire alors à des résultats aberrants.

Cas unitaires utilisés pour la méthode des coefficients
Il est préférable d’extérioriser les effets des modifications du schéma statique de la façon suivante (Figure 7) :
-
cas 1 : calcul de l’état à terme, si le clavage n’était pas réalisé ;
-
cas 2 : calcul juste avant clavage, avec le module de béton adéquat ;
-
cas 3 : calcul de l’effet du clavage : appliquer à la structure un déplacement imposé au niveau du clavage, ramenant la valeur de la discontinuité (dans le cas de l’exemple, en rotation) à la valeur figée par le clavage ;
-
l’état à terme est la somme des cas 1 et 3.
Cette technique est plus facilement extensible aux cas où les modifications de la configuration statique des ouvrages sont nombreuses.

Cas unitaires utilisés pour la méthode de superposition
Il n’est pas inutile de rappeler que, sous les effets de déformation différée, le béton réagit avec un module de déformation apparent, appelé module de relaxation, plus faible que le module de fluage correspondant. Si le rapport classique entre le module de l’acier et du béton, intégrant les effets de fluage, est de l’ordre de 18, dans le cas d’un déplacement imposé, ce rapport passe à une valeur de 24. Ceci a tendance à rendre moins efficaces les réglages par dénivellation d’appui et par vérinage, lorsque ce dernier conduit à imposer une déformation à la structure.
Du point de vue des simulations éléments finis, le nombre important d’états intermédiaires à traiter multiplie le risque d’erreurs. Les vérifications doivent porter :
-
sur le respect des conditions limites dans les phases intermédiaires ;
-
sur le respect des déplacements gelés par les phases de construction dans la structure (par exemple, discontinuité de pente au niveau de clavages).
En études d’exécution, il faut aussi rappeler que le fluage réel du béton peut s’écarter fortement des formulations théoriques ; il faut donc construire le modèle de telle façon qu’il soit aisé de l’adapter pour restituer les déformations apparaissant dans les premières phases, et ainsi améliorer la prédiction des phases suivantes.
$translationBooksChapitre E - Post-traitements typiques du génie civil
Chapitre E - Post-traitements typiques du génie civil
Introduction
La variété des quantités d’intérêt analysées pour des ouvrages de génie civil est importante car elle découle de la grande diversité de ce qui peut être étudié compte tenu de :
-
la nature de l’ouvrage considéré et donc des exigences fonctionnelles qui lui sont associées (par exemple l’étanchéité pour un barrage, un réservoir, une enceinte de confinement de centrale nucléaire (ouverture de fissure, état de contrainte, déformations résiduelles, …),
-
les états limites considérés (ultimes ou de services, …),
-
la nature des cas de charge (dynamique, statique, différé, …),
-
les éléments structurels constitutifs (béton massif, armé, précontraint, construction métallique, bois, ouvrages en maçonnerie, …).
Par ailleurs, les quantités d’intérêt requises peuvent être directement ou non accessibles à l’issue d’un calcul EF. Elles peuvent être construites à partir de produits du calcul qui pourront permettre par post-traitement de fournir la quantité d’intérêt qui sera ensuite comparée à un critère ou qui sera ensuite une donnée pour la suite du projet (sections d’armatures, orientations de barres de ferraillages, …).
Les Eurocodes permettent de savoir quelles sont les grandeurs à analyser compte tenu des différents cas cités plus haut. En revanche, il n’est pas établi dans les codes et normes comment avoir accès à ces grandeurs. Ce chapitre permet de fournir les clés permettant de savoir comment y accéder et les pièges à éviter.
E.1 Généralités
E.2 Grandeurs en dynamique
E.3 Cas spécifique du béton armé
E.3 Cas spécifique du béton armé
$translationBooksE.1 Généralités
E.1 Généralités
Les différentes grandeurs post-traitées peuvent différer très significativement en fonction de la finalité de l’analyse faite par éléments finis.
Typiquement, les grandeurs étudiées au titre d’études de prédimensionnement (esquisse ou Avant Projet Sommaire) sont très différentes de ce que l’on va chercher à obtenir en Avant Projet Détaillé et a fortiori en études d’exécution. Lorsqu’il s’agit d’analyser le comportement d’un ouvrage existant pour quantifier un éventuel risque structurel les quantités d’intérêt sont encore différentes.
On serait tenté de considérer :
-
Phases de prédimensionnement (esquisse, APS, …) : grandeurs de type déplacements, flèches rapportées à des portées, etc …,
-
Phases de dimensionnement : densités de ferraillage pour des plaques, sections de ferraillage pour des poutres et poteaux, ouverture de fissure, …
-
Analyse structurelle : états de contraintes (contraintes principales dans le béton: directions, signes, tri-axialité et valeurs, comparaison à des critères, par exemple Ottosen, Rankine, Drucker-Prager si l’analyse est élastique), déformations principales directions, valeurs et signes, cartes d’endommagement, contraintes dans les aciers, déformations plastiques, …
Enfin, il importe de garder à l’esprit que toutes les quantités d’intérêt ne sont pas accessibles pour tous les différents types d’éléments et modèle de comportement. En effet, le type d’élément conditionne la nature des degrés de liberté : on n’a pas accès à des rotations aux nœuds et pas de moments vec des éléments volumiques de base. De la même façon, un modèle de plasticité ne peut fournir de valeurs d’endommagement. Ces éléments peuvent paraître triviaux mais ils sont suffisamment souvent oubliés par les utilisateurs des codes de calcul qu’il nous paraissait utile de le rappeler ici.
1. Contraintes et déformations
Comme cela est exposé dans le chapitre « Généralités », les champs de contraintes et déformations ne sont pas des produits de calcul directs d’une résolution d’un problème de mécanique par un solveur aux éléments finis. Ils sont déduits des déplacements par dérivations des champs interpolés de déplacements. On note en conservant les notations du chapitre généralités :
![]()
En élasticité linéaire, la relation contrainte – déformation s'écrit (avec H la matrice de Hooke) :
![]()
Dans ce genre de démarche, les champs de contrainte et de déformation évoluent selon des fonctions d’interpolation de degré inférieur à celle des déplacements.
En analyse non linéaire les contraintes et déformations ne peuvent pas être ainsi évaluées par un produit de la matrice de Hooke et de la dérivée des déplacements nodaux et s’appuient sur les valeurs aux points de Gauss pour un élément en faisant appel aux fonctions de forme pour les extrapoler sur le reste de l’élément et aux nœuds. Cette démarche permet en outre de faire en sorte que les contraintes évoluent selon le même degré que les fonctions d’interpolation et non leurs dérivées.
A titre d’exemple, sur un élément qui a n nœuds, npg points de Gauss situés aux coordonnées ξnpg, munis de fonctions de forme Ni, on retient la minimisation au sens des moindres carrés entre le champ interpolé évalué à partir des valeurs nodales recherchées et les valeurs gaussiennes connues.

Construction des valeurs nodales élémentaires à partir des valeurs aux points de Gauss en 1D
Soit donc il s’agit de minimiser la fonctionnelle :


Soit pour chaque nœud i parmi les n nœuds de l’élément :

Qui peut se mettre sous une forme matricielle dont les matrices sont connues une fois pour toute pour les éléments isoparamétriques de référence :

Et donc, on obtient directement les valeurs nodales de contrainte :

Il peut donc exister plusieurs valeurs nodales de déformation ou de contrainte pour un nœud commun à plusieurs éléments. Les valeurs nodales doivent être déduites à partir de ces valeurs.

Discontinuité des valeurs nodales élémentaires en 1D
Il existe diverses méthodes permettant de reconstituer la continuité des déformations ou des contraintes (si les matériaux sont les mêmes entre deux éléments contigus) en ayant une seule valeur nodale de déformation (ou de contrainte). Il s’agit de lissage des champs de contrainte et de déformation par certains codes de calculs sur la globalité de la géométrie (par minimisation au sens des moindres carrés) ou par des moyennes des valeurs provenant pour un nœud des éléments auxquels il appartient tel que cela figure dans la figure 3 pour un cas 1D.

Exemple de construction d’une valeur nodale moyenne des valeurs nodales élémentaires en 1D
Pour des raisons de visualisations on peut préférer de faire apparaître des grandeurs élémentaires lissées. Cependant, lorsqu’il s’agit de rechercher de la précision les grandeurs calculées et déduites au point de Gauss seront à privilégier.
2. Passage des contraintes de la mécanique des milieux continus aux efforts de la mécanique des structures
Les méthodes automatisées de calcul de ferraillage s’appuient sur des algorithmes en flexion composée sur base de torseurs de type plaque et coque à 8 composantes ou en flexion composée déviée sur base torseurs de type poutre à 6 composantes.
Certains ouvrages peuvent nécessiter pour diverses raisons de prendre en compte une modélisation volumique de l’ouvrage (barrage, structures de types réservoirs précontraints : réservoir de Gaz Naturel Liquéfié, enceintes de confinement). Pour décliner une démarche calculatoire sur base de torseurs à 8 composantes, il est nécessaire de reconstruire des efforts internes de mécanique des structures à partir des champs de contraintes le long de segments comme cela est exposé figure ci-dessous.

Segment le long duquel les contraintes servent de référence pour la reconstruction d’un torseur coque
On considère le tenseur des contraintes exprimé le long du segment de la figure précédente :

En toute rigueur, pour une plaque mince satisfaisant les hypothèses de Kirschhof-Loeve, on considère le torseur coque à 10 composantes que l’on associe aux contraintes suivant le principe d’équivalence :

Cette intégration continue est en réalité discrète le long du segment et typiquement peut se réaliser à parti des valeurs des contraintes exprimées au point de Gauss ou aux nœuds.
Diverses techniques d’intégration peuvent être utilisées (Trapèze, Gauss, Lobatto, etc …).
On conservera par la suite et à des fins de simplicités une expression continue même si celle-ci n’est pas rigoureuse dans le contexte discrétisé des valeurs obtenues par éléments finis.
Compte tenu du théorème de Cauchy égalisant les contraintes de cisaillement de facettes adjacentes, ce torseur se réduit à 8 composantes :

Considérer que cette plaque est une dalle isotrope conduit à négliger les contributions des efforts de membrane.

Il ressort donc un torseur à 5 composantes (en considérant que la notation M_x désigne le moment sollicitant les aciers dans la direction e_x) qui sont les actions mécaniques internes d’un élément plaque :

(1) Effort tranchant hors plan (direction z) pour la facette de normale x,
(2) Effort tranchant hors plan (direction z) pour la facette de normale y,
(3) Moment de flexion faisant travailler les aciers dans la direction x,
(4) Moment de flexion faisant travailler les aciers dans la direction y,
(5) Moment de torsion de la section de la dalle de normal x ou y.
3. Méthode des coupures : éléments de réduction élémentaires (EF) à éléments de réduction structurels de type poutre
Dans certains les contraintes du projet peuvent amener à modéliser intégralement une structure par plaque y compris dans des zones où celles-ci ne sont pas appropriées tels que les trumeaux et les linteaux.
Dans ces zones, il incombe de reconstituer un torseur de type poutre pour apprécier plus proprement le comportement local, en particulier pour estimer le ferraillage requis.
Une pratique répandue répondant à ce besoin est la réalisation de coupures et l’estimation des efforts sur cette coupure.
La coupure doit est choisie judicieusement de façon à adhérer aux hypothèses d’Euler-Bernoulli concernant les sections de type qui doivent rester planes et droites. C’est généralement le cas des trumeaux et linteaux.

Exemple de coupures dans un linteau ou un trumeau passant ou ne pas passant pas par des nœuds
On construit dans le repère local de la coupure les éléments de réduction de poutre à part des éléments de réduction de coque. Ceux-ci peuvent être des efforts aux nœuds ou des efforts évalués en un point quelconque de l’élément coïncidant avec la ligne de coupure et évalués au moyen des fonctions de forme élémentaires.
On écrit dans le cas de l’exemple de la figure 5 pour la ligne de coupure du linteau où le repère global et le repère de la ligne coïncident :

(1) Effort normal à la section de la poutre assimilée i.e. la coupure,
(2) Effort tranchant dans le plan,
(3) Effort tranchant hors plan,
(4) Moment de flexion dans le plan,
(5) Moment de flexion hors plan,
(6) Moment de torsion.
$translationBooksE.2 Grandeurs en dynamique
E.2 Grandeurs en dynamique
1) Analyses temporelles
Le post-traitement des grandeurs temporelles ne présente pas de difficulté majeure tant que l’on ne s’intéresse pas à cibler un instant précis où à caractériser une valeur unique représentative de l’ensemble des instants couverts par l’analyse.
Pour les cas où le chargement est maîtrisé et ne présente pas de caractère aléatoire, une seule analyse peut suffire. S’il est privilégié d’extraire une grandeur scalaire représentative de l’ensemble des instants, le choix de la norme incombe à l’ingénieur qui analyse les résultats et qui devra être en mesure de le justifier. Une caractérisation statistique peut également être pertinente (percentile typiquement).
Pour le cas où l’ingénieur s’intéresse à extraire un ensemble de grandeurs constituants un vecteur, la problématique de la concomitance des grandeurs normées (valeurs absolue, maximale, minimale, …) se pose. L’instant où un moment est maximal en un point pour un torseur ne coïncide pas nécessairement avec l’extremum d’un effort de cisaillement.
Lorsque le chargement revêt un caractère aléatoire, il importe de multiplier le nombre de cas de calculs en intégrant le caractère aléatoire du chargement. A titre d’exemple, si on considère N cas de calculs et que l’on construit pour une quantité d’intérêt gi(t) la valeur de dimensionnement Gi correspondante pour un cas i (il peut s’agit de la valeur positive max et aussi de la valeur négative max pour les intégrer ensuite dans une démarche de concomitance d’actions).
On considère :
-
La valeur de dimensionnement retenue qui peut être (à titre d’exemple) :



-
Sa moyenne,

-
Son écart type :

-
L’estimation de la moyenne de la population de la valeur G pour les N résultats de calculs :

Où λ(N) est calculé à partir de la variable de Student pour N échantillons (cas de calculs) pour un niveau de confiance 95% (unilatéral) tel que :

Le tableau ci-dessous fournit des estimations de la moyenne pour des nombres de cas de calculs variables.
| N calculs | t0.05;N-1 | λ(N) | N calculs | t0.05;N-1 | λ(N) | N calculs | t0.05;N-1 | λ(N) | N calculs | t0.05;N-1 | λ(N) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 6.3137 | 4.46 | 15 | 1.7613 | 0.45 | 28 | 1.7033 | 0.32 | 41 | 1.6839 | 0.26 |
| 3 | 2.9200 | 1.69 | 16 | 1.7531 | 0.44 | 29 | 1.7011 | 0.32 | 42 | 1.6829 | 0.26 |
| 4 | 2.3534 | 1.18 | 17 | 1.7459 | 0.42 | 30 | 1.6991 | 0.31 | 43 | 1.6820 | 0.26 |
| 5 | 2.1318 | 0.95 | 18 | 1.7396 | 0.41 | 31 | 1.6973 | 0.30 | 44 | 1.6811 | 0.25 |
| 6 | 2.0150 | 0.82 | 19 | 1.7341 | 0.40 | 32 | 1.6955 | 0.30 | 45 | 1.6802 | 0.25 |
| 7 | 1.9432 | 0.73 | 20 | 1.7291 | 0.39 | 33 | 1.6939 | 0.29 | 46 | 1.6794 | 0.25 |
| 8 | 1.8946 | 0.67 | 21 | 1.7247 | 0.38 | 34 | 1.6924 | 0.29 | 47 | 1.6787 | 0.24 |
| 9 | 1.8595 | 0.62 | 22 | 1.7207 | 0.37 | 35 | 1.6909 | 0.29 | 48 | 1.6779 | 0.24 |
| 10 | 1.8331 | 0.58 | 23 | 1.7171 | 0.36 | 36 | 1.6896 | 0.28 | 49 | 1.6772 | 0.24 |
| 11 | 1.8125 | 0.55 | 24 | 1.7139 | 0.35 | 37 | 1.6883 | 0.28 | 50 | 1.6766 | 0.24 |
| 12 | 1.7959 | 0.52 | 25 | 1.7109 | 0.34 | 38 | 1.6871 | 0.27 | 51 | 1.6759 | 0.23 |
| 13 | 1.7823 | 0.49 | 26 | 1.7081 | 0.33 | 39 | 1.6860 | 0.27 | 55 | 1.6620 | 0.22 |
| 14 | 1.7709 | 0.47 | 27 | 1.7056 | 0.33 | 40 | 1.6849 | 0.27 | 60 | 1.6558 | 0.21 |
2) Analyses spectrales sismiques
Les analyses spectrales sismiques fournissent des grandeurs représentatives de la moyenne d’un extremum où cours du temps.
L’objet de ce paragraphe est d’attirer l’attention du lecteur sur des précautions importantes à prendre pour éviter de commettre des erreurs importantes dans le calcul de résultats issus d’un cumul quadratique.
Comme cela est évoqué dans le chapitre dynamique, il est possible de cumuler quadratiquement simplement ou de manière complète les réponses spectrales de chaque mode. Le résultat de ces cumuls est une valeur positive.
Il importe de considérer que toute opération que l’on souhaite réaliser sur une quantité d’intérêt qui fait l’objet d’un cumul quadratique (simple ou complet) des réponses spectrales de chaque mode doit être réalisée avant le cumul.
Prenons une illustration simple avec la différence entre le déplacement de deux nœuds A et B cumulés simplement sur 2 modes 1 et 2 (une illustration avec une combinaison CQC serait juste plus lourde en écriture en faisant intervenir les termes croisés) :
En toute rigueur, la différence évoquée à titre d’exemple s’écrit :

Il est donc assez évident de voir qu’estimer a posteriori du cumul la différence est largement erroné :

La première valeur est toujours positive mais elle intègre des écarts algébriques de quantités sur un même mode. La seconde expression peut en outre conduire à sous-estimer drastiquement une réponse extremum. On peut par ailleurs démontrer en ayant recours à l’inégalité de Cauchy-Schwartz que la première estimation est la borne supérieure de la valeur absolue du calcul erroné présenté dans la seconde formule.
On peut également prendre une illustration plus complexe avec l’estimation d’une contrainte de von Misès sur la base des contraintes principales pour 2 modes :

Une estimation a posteriori du cumul des contraintes de von Misès est largement erronée :

Exemple d’application spécifique : estimation de l’ouverture d’un joint entre deux bâtiments
En ingénierie sismique, il est nécessaire d’estimer l’ouverture d’un joint entre deux bâtiments sous séisme pour garantir que l’on se prémunira de tout risque d’entrechoquement. La pratique admise consiste à calculer indépendamment les valeurs extrêmes de déplacement de l’enveloppe de chaque bâtiment sur la base d’un cumul quadratique puis d’évaluer l’ouverture maximale du joint en calculant la différence entre ces deux valeurs positives. On prend ainsi en compte une opposition de phase défavorable des réponses maximales.
$translationBooksE.3 Cas spécifique du béton armé
E.3 Cas spécifique du béton armé
1) Aperçu des méthodes usuelles de détermination du ferraillage pour des éléments de plaque
Il existe principalement 3 méthodologies applicables aux plaques pour lesquels le lecteur pourra consulter les références associées :
-
Méthode des lignes de rupture de Johansen :
-
Save M.A., Massonet C.E., De Saxcé G. – Plastic limit analysis of plates, shells and disks, Applied Mathematics and Mechanics Vol. 43.
-
Cette méthode est applicable pour des plaques faiblement armée (taux d’armature inférieur à 0.7%) permettant de valoriser l’apparition de lignes de rupture et de mettre en place un ferraillage qui s’y oppose.
-
-
Méthode sandwich :
-
Marti, P., Design of concrete slabs for transverse shear, ACI Structural Journal, Vol. 87, pages 180 à 190.
-
Cette méthode prend intrinsèquement le comportement de plaque dans son fonctionnement, elle est codifiée dans les annexes LL et MM de l’Eurocode 2 partie 2,
-
-
Méthode de Capra et Maury :
-
Capra A. at Maury J.-F., Calcul automatique du ferraillage optimal des plaques et coques en béton armé, Annales de l’Institut Technique du Bâtiment et des travaux publics, n°367, Décembre 1978,
-
Cette méthode s’appuie sur l’équilibre de section unitaire en flexion composée, elle est détaillée dans la suite de la section.
-
2) Exemple de la méthode de Capra-Maury
On définit un ensemble de facettes, centrées au point de calcul du code aux éléments finis. Il peut s’agir d’un nœud, d’un point de Gauss ou d’un point quelconque où les efforts sont interpolés.
Sa normale tourne de ce point dans le plan tangent au feuillet moyen. La facette est repérée par l’angle θ que fait sa normale avec l’axe OX du repère de l’élément (voir figure 2.1-a). L’angle θ est discrétisé régulièrement de -90°à +90° (ici avec un pas de 5°). Les axes Ox et Oy sont les axes des nappes d'armatures.

Facette de référence parallèle à la section de poutre équilibrée en flexion composée
Pour chacune de ces facettes, on évalue le moment de flexion (M), l’effort de membrane (N) et l'effort tranchant (V) qui s’y appliquent en fonction des tenseurs des efforts à l’aide des équations :



Par un calcul en flexion composée, on détermine les sections d'acier en nappes supérieure et inférieure AS(θ) et AI(θ) d'acier requise dans la direction θ pour équilibrer la section dans le contexte réglementaire de béton armé retenu.
Les efforts résistants dans la direction θ des deux nappes peuvent être évalués à l’aide des expressions

où fyd représente la contrainte maximale admissible de l’acier (identique dans les deux directions).
La résistance est assurée si l’effort résistant est supérieur à l’effort appliqué, ce qui s’écrit :


Ainsi, en considérant un repère orthonormé comportant AXS en abscisse et AYS en ordonnée, on a à résoudre finalement pour les ferraillages supérieur et inférieur :
 pour tous les angles θ
pour tous les angles θ
 pour tous les angles θ
pour tous les angles θ
et
 et
et  minimum.
minimum.
Les inégalités sur la résistance définissent pour chaque valeur de θ un demi-espace limité par une droite de pente négative qui traduit un domaine de validité tel que cela est représenté figure suivante.

Domaine de résistance pour une facette θ
En parcourant toutes les valeurs de θ, on obtient le domaine de validité indiqué sur la figure suivante, délimité par la ligne brisée ABCD …

Domaine de résistance pour l’ensemble des facettes
Pour chaque point P du domaine de validité, la section totale des armatures peut être obtenue en projetant le point P en Q sur la première bissectrice. La distance OQ représente alors la valeur  avec AS = AXS + AYS.
avec AS = AXS + AYS.
On constate donc que l’optimum de ferraillage correspond à l'un des 36 points (compte tenu du pas de rotation des facettes retenu si on prend une facette tous les 10 degrés par exemple) de la frontière (illustration par les 4 points de la ligne brisée ABCD …) dont la projection sur la première bissectrice est la plus proche de l’origine des axes. La recherche de ce point peut être effectuée par une méthode de type « dichotomie ».
3) Méthodes des bielles et tirants à partir d’un résultat de calcul aux éléments finis
En présence d'éléments structurels soumis à des charges ponctuelles importantes ou présentant des modifications brusques de leur section et de leur géométrie, les méthodes classiques d'analyse des sections planes ne sont pas satisfaisantes. Ces lieux sont généralement ferraillés à l'aide de règles de bonnes pratiques basées sur l'expérience ou sur des directives empiriques. La méthode bielles-tirants (MBT) est une procédure de conception rationnelle pour les éléments structurels complexes ; la procédure a une base en mécanique, mais elle est assez simple pour être facilement appliquée dans la conception.
De manière générale, la MBT implique l’idéalisation d’un élément structurel complexe en une simple structure capable de représenter le cheminement des contraintes au sein de l’élément.
Le treillis est composé de bielles modélisant les champs de compression du béton, de tirants représentant une armature en acier élastique et de nœuds représentant les zones localisées où les éléments s’interconnectent ou les zones où l’acier élastique est ancré dans le béton. Les bielles et les tirants ne portent que des forces uniaxiales. Ce mécanisme doit être stable et équilibrer correctement les charges appliquées.
La ruine de la structure est dictée par la rupture d'un ou plusieurs tirants ou également définie par des contraintes de compression excessives à l'intérieur des bielles ou des nœuds. Idéalement, seul le premier mode de défaillance devrait se produire.

Exemple de région D et de modélisation du système pour obtention des champs de contraintes puis des efforts aux appuis du treillis BT
On applique cette méthode pour des régions dites D. Pour caractériser ces régions, on considère que la répartition des déformations sur la profondeur de l’élément présente un profil non linéaire.
Par conséquent, les hypothèses sous-jacentes à la procédure de conception de coupe sont invalidées. On ne peut y décliner le principe d’équivalence
Selon le principe de Saint Venant, une analyse des contraintes élastiques indique que les contraintes dues aux forces axiales et à la flexion se rapprochent d’une distribution linéaire à une distance approximativement égale à la profondeur de l’élément, h, à l’écart de la discontinuité.
En d'autres termes, une distribution de contrainte non linéaire existe dans la profondeur d'un membre à partir de l'emplacement où la discontinuité est introduite. Ensuite, on peut affirmer que les régions D sont supposées s’étendre jusqu’à une distance h de la charge appliquée et des réactions de support. En général, une région d'un élément structurel est supposée être dominée par un profil non linéaire, ou une région D, lorsque le rapport étendue / profondeur, a / h, est inférieur à 2 ou à 2,5. L'étendue de cisaillement, a, est définie comme la distance entre la charge appliquée et le support le plus proche dans les éléments simples.
L’approche à suivre pour définir un treillis bielle-tirant peut être résumé dans la figure 10.

Principe général de conception par MBT
Les méthodes de vérifications sont codifiées dans l’Eurocode 2 partie 1-1.
La démarche présentée dans la figure 10 est complexe à mettre en œuvre et dépend fortement de l’ingénieur qui la met en œuvre.
Des approches se développent de plus en plus dans ce registre pour chercher à automatiser la démarche. En France, le code aux éléments code_aster intègre un opérateur CALC_BT qui permet de rendre semi-automatique la démarche sur la base :
-
d’une analyse des champs pics locaux des champs de contraintes principales majeures et mineures,
-
d’un découpage de la région D modélisée par un pavage de Voronoï,
-
par projection des directions moyennes des contraintes principales dans les pavés de Voronoï
-
un ensemble de procédés d’optimisation.

Exemple de référence à gauche – Solution obtenue automatiquement par l’opérateur CALC_BT de code_aster
Cette méthode nécessite un niveau d’expérience important et un contrôle par un expert.
$translationBooksChapitre F - Calculs géotechniques
Chapitre F - Calculs géotechniques
Introduction
Les méthodes classiques de conception et de dimensionnement des ouvrages géotechniques concernent, en majorité, l’analyse de la résistance vis-à-vis de la rupture d’un ouvrage isolé. Ces méthodes analytiques ou semi-analytiques ne prennent en compte que des géométries très simples, et fournissent peu ou pas d’informations sur les déformations du terrain qui entoure les ouvrages.
L'utilisation de plus en plus intensive de l’espace et du sous-sol urbains, occupés par des ouvrages variés proches les uns des autres, impose de maîtriser les interactions entre ouvrages. Le concepteur d’un ouvrage doit justifier que les déplacements induits par sa construction demeurent en-deçà de seuils fixés par le maître d’ouvrage. Les méthodes traditionnelles ne répondent pas à ce besoin, et cela explique le recours de plus en plus fréquent à la modélisation numérique, à l’aide de logiciels dédiés à la géotechnique et adaptés au travail en bureau d’études. De manière plus précise, la modélisation numérique est utilisée dans deux situations différentes :
-
au stade du projet, pour justifier un dimensionnement, lorsque les méthodes traditionnelles sont difficiles ou impossibles à mettre en œuvre ;
-
comme outil d'expertise, pour étudier le comportement d'un ouvrage endommagé, identifier les phénomènes responsables d’une pathologie, et justifier l’utilisation d’une méthode de confortement.
Selon le cas, on utilise des modèles plus ou moins complexes, en tenant compte de l'incertitude sur le comportement des sols naturels et de leur variabilité spatiale. Cette incertitude se traduit par la difficulté de choisir un modèle de comportement et d’en déterminer les paramètres. L'utilisateur doit souvent faire un choix entre un modèle robuste, dont il comprend bien le fonctionnement, mais qui ne rend pas compte de toute la complexité du comportement du sol, et un modèle potentiellement plus fidèle au comportement réel des sols, mais comportant de nombreux paramètres dont le rôle est parfois difficile à cerner et qui sont difficiles à mesurer.
La philosophie des règles de dimensionnement encourage à la première approche, et à utiliser des modèles simples et robustes, et à assurer la sécurité du dimensionnement en affectant les résultats de facteurs appropriés et en effectuant des études paramétriques pour estimer la sensibilité des résultats vis-à-vis des paramètres, mais cette approche fait courir le risque de trop simplifier le problème rencontré, ou de conduire à des dimensionnements excessivement conservatifs, et inutilement coûteux.
L'autre approche consiste à utiliser des modèles de comportement qui tentent de mieux représenter les différents aspects du comportement des sols. Un très grand nombre de modèles ont été proposés, mais leur utilisation pratique reste difficile. D’autre part, il faut aussi lutter contre l’illusion d’avoir le modèle « universel » qui décrit tous les phénomènes. Il est nécessaire de cerner les limites du modèle retenu : un modèle élastique parfaitement plastique ou avec un écrouissage isotrope, même avec une surface de charge et une loi d'écrouissage complexes, ne permet pas de prédire une accumulation progressive de déformation dans un massif de sol.
L'utilisation des éléments finis demande donc de la part de l'utilisateur un recul critique sur le modèle de comportement du sol. Mais ce n'est pas le seul aspect important : le résultat des calculs peut dépendre de manière essentielle de la géométrie tridimensionnelle de l’ouvrage et de celle des couches de sol. Il est parfois (pas toujours) justifié de simplifier la représentation du comportement des sols et de privilégier celle du processus de construction. En tout état de cause, il conviendra de contrôler soigneusement les résultats des simulations numériques.
Enfin, il est clair que les ouvrages géotechniques sont constitués de terre, au contact de la terre, ou enterrés totalement ou partiellement, et que la modélisation numérique doit donc représenter l’interaction mécanique entre le sol et la structure.
Ce chapitre est organisé comme suit : il récapitule les principales spécificités des calculs numériques en géotechnique, avant de présenter succinctement les principes de vérification adoptés dans l’Eurocode 7. Une fois ces éléments présentés, on propose des recommandations visant à une bonne pratique des calculs par éléments finis en géotechnique. Il aborde également les spécificités des calculs en dynamique.
F.1 Aspects géométriques
F.2 Non-linéarités matérielles
F.2 Non-linéarités matérielles
F.3 Interactions sol-structure
F.3 Interactions sol-structure
F.4 Effets hydrauliques
F.5 Incertitudes et recommandations
F.5 Incertitudes et recommandations
F.6 Aspects normatifs : Principes de l'Eurocode 7
F.6 Aspects normatifs : Principes de l'Eurocode 7
F.7 Modélisation en dynamique
F.8 Échelles caractéristiques
Conclusions et références
Ce chapitre présente un panorama des difficultés posées spécifiquement par les calculs par éléments finis en géotechnique, en statique ou en dynamique. Des précautions particulières doivent être prises pour la mise en œuvre des calculs, concernant le maillage, les conditions aux limites, le phasage, le choix des modèles de comportement et le calage des paramètres.
Moyennant une certaine habitude, et la préoccupation constante de contrôler les résultats obtenus, on est en mesure de traiter une large gamme de problèmes et d’ouvrages. Il reste cependant des situations qu’il est difficile et/ou coûteux de traiter numériquement.
En premier lieu, des difficultés peuvent provenir du fait que la structure mathématique des problèmes étudiés pose problème : en dynamique, le choix de pas de temps cohérents avec toutes les données du calcul reste délicat ; en statique, la gestion de plusieurs non-linéarités de natures différentes (contact unilatéral, endommagement) peut conduire à des difficultés numériques difficiles à surmonter.
Il faut aussi rappeler que la physique de certains phénomènes reste mal maîtrisée ou mal décrite, et le traitement numérique reflète cette situation : c’est le cas pour l’initiation et l’évolution des glissements de terrain, les conditions d’exécution des travaux comme le compactage des matériaux de remblai, l’état initial des contraintes, de la teneur en eau et d’autres paramètres liés à l’histoire des matériaux en place, etc.
Pour les références spécifiques, se reporter à la bibliographie :
F.1 Aspects géométriques
F.1 Aspects géométriques
L’un des atouts de la méthode des éléments finis réside dans la possibilité de décrire la géométrie exacte des ouvrages, y compris au cours des différentes phases de construction. Des outils de pré-traitement proches de la CAO permettent de générer facilement des géométries très complexes. Une des spécificités des ouvrages géotechniques réside dans le fait qu’il faut en général prendre en compte dans le maillage le massif de terre qui constitue ou qui entoure l’ouvrage lui-même.
1) Limites du domaine d'étude
Une première difficulté consiste à cerner les limites du domaine pris en compte dans l’étude. Pour un ouvrage géotechnique, les limites horizontales et la limite inférieure du domaine d’étude sont rarement précisément déterminées : on limite l’étendue du domaine d’étude par des plans verticaux, dont la position est fixée généralement suivant des règles empiriques.
En déformation plane par exemple, la position à laquelle on fixe la limite inférieure du maillage a une influence directe sur le tassement calculé pour une semelle filante ou au-dessus d’un tunnel. Cette influence est nette dans le cas d’un massif de sol élastique linéaire homogène. On peut la réduire en prenant en compte des modules élastiques qui augmentent avec la profondeur, mais elle reste néanmoins susceptible d’induire une erreur significative dans les déplacements calculés. Le cas idéal est celui où l’on a reconnu un substratum rigide à une profondeur donnée, ce qui suppose que les reconnaissances aient été conduites jusqu’à une profondeur suffisante. Pour un tunnel, par exemple, il serait souhaitable, pour les besoins de la modélisation, de mener des reconnaissances bien au-delà de la profondeur de l’axe : ce n’est généralement pas le cas dans les projets réels.
Dans les directions latérales, la prise en compte d’un domaine trop peu étendu peut également modifier significativement la réponse du modèle numérique. Des déplacements bloqués conduisent à surestimer la raideur du massif, des conditions de type « contact lisse » conduisent à l’inverse à surestimer les déplacements. Le choix des dimensions du maillage adaptées à un ouvrage reste un problème largement ouvert, même si certains auteurs ont proposé des règles pratiques, qui ne doivent cependant pas être prises comme des prescriptions absolues (voir Mestat et Prat, 1999).
Le choix de l’étendue du domaine pris en compte dans le maillage est donc un point important de la modélisation des ouvrages géotechniques, même pour des analyses relativement simples en statique. Dans le cas des calculs dynamiques, la question de l’étendue du domaine maillé soulève des difficultés spécifiques et fait partie intégrante de la stratégie de modélisation. On détaillera ce point dans la section 8 ci-dessous.
2) Hétérogénéités du sol
Dans certaines régions, comme celles de Londres ou de Francfort, la géologie permet de considérer le sol au voisinage de l’ouvrage comme homogène (au sens où son comportement mécanique et hydraulique peut être représenté par un modèle unique). Cependant, il est fréquent, dans d’autres contextes, en particulier dans la région parisienne, que le domaine étudié comporte plusieurs couches de terrains présentant des natures et des caractéristiques (en particulier mécaniques) bien différentes. L’élaboration d’un modèle commence donc, comme pour les méthodes traditionnelles, par une étude détaillée des couches de sol dans la zone intéressée par l’ouvrage. Il ne s’agit pas de reproduire la géométrie exacte des couches géologiques (qui peuvent être de faible épaisseur localement), mais de définir des ensembles géotechniquement homogènes.
3) Discontinuités
Une particularité importante des calculs géotechniques réside dans la présence, au sein des massifs, de surfaces de fracture préexistantes à la mise en place de l’ouvrage ou du chargement étudié. Elles produisent une discontinuité du déplacement entre les blocs situés de part et d’autre de la surface de fracture. La méthode des éléments finis est plutôt adaptée à la recherche de champs de déplacement continus, et la prise en compte de ce type de discontinuité demande la mise en œuvre de techniques spécifiques (on utilise généralement des éléments particuliers), voire d’utiliser une autre méthode de calcul comme la méthode des éléments distincts.
L’analyse a posteriori de glissements de terrain, par exemple, est un exercice délicat. Il est à l’heure actuelle extrêmement difficile de prévoir l’apparition et le développement d’une surface de rupture. On en est réduit le plus souvent à prendre en compte une surface existante, dont on a pu reconnaître la position de manière plus ou moins précise à l’aide de dispositifs ad hoc (par exemple des inclinomètres qui suivent la déformation d’un versant).
Les massifs rocheux sont souvent traversés par un grand nombre de fractures présentant des orientations pratiquement parallèles à une ou deux directions privilégiées (diaclases régionales). La distribution des fractures est aléatoire, ou en tout cas impossible à caractériser complètement à l’échelle du massif, et diffuse. Si l’on s’intéresse au comportement global du massif, on peut proposer de le modéliser comme un milieu continu, en lui affectant un modèle de comportement intégrant, à l’échelle du calcul, l’effet des discontinuités : on recourt en général à des méthodes d’homogénéisation.
On peut aussi avoir à prendre en compte une discontinuité de grande ampleur dans un massif rocheux (faille), que l’on peut traiter comme les surfaces de rupture des glissements de terrain.
4) Un système matériel "ouvert" et des techniques de construction à modéliser
Comme on l’a dit dans le chapitre introductif, une spécificité des calculs de génie civil tient à la nécessité de prendre en compte des phases de construction, telle que le déblaiement ou le remblaiement, la prise d’un massif de béton, la mise en tension de câbles, etc. La prise en compte de ces phases de construction dans le cadre de la méthode des éléments finis n’est pas forcément simple et immédiate : la méthode consiste à se ramener au calcul d’une matrice de rigidité, d’un vecteur de forces nodales, et à résoudre le système obtenu en tenant compte des conditions aux limites. Pour modéliser les phases de construction, on est amené à enchaîner des calculs, en prenant en compte le changement de raideur de certains éléments, la disparition ou le changement de nature de certains appuis, des changements de point d’application des chargements, etc.
La difficulté consiste donc à proposer des techniques de simulation permettant de prendre en compte un grand nombre de dispositions constructives dans le cadre relativement étroit de la méthode des éléments finis. Il revient à l’utilisateur de discerner si les outils de modélisation proposés par les logiciels reflètent correctement les phénomènes mis en jeu.
Dans le cas des tunnels creusés au tunnelier, les sollicitations appliquées au terrain au cours des différentes phases d’avancement sont complexes, le terrain se refermant sur l’anneau constitué par les voussoirs lorsque le tunnelier avance. La mise en place de pieux par battage est un autre exemple de problème qu’il est difficile de ramener au cadre de la méthode des éléments finis.
$translationBooksF.2 Non-linéarités matérielles
F.2 Non-linéarités matérielles
En géotechnique, il est très rare de pouvoir se limiter à un comportement linéaire pour l’étude d’un ouvrage (à l’exception de certaines analyses dynamiques). Pour autant, il peut être utile de réaliser dans un premier temps un calcul linéaire, pour vérifier que la géométrie et les conditions aux limites sont correctes et se faire une première idée de la déformation que le chargement peut provoquer. Cette première idée peut cependant être complètement fausse : dans le cas d’une excavation devant une paroi moulée par exemple, la cinématique calculée avec un comportement linéaire est nettement différente de celle que l’on observe.
1) Lois de comportement
Même en se limitant aux cas parfaitement saturé ou parfaitement sec, le comportement des sols est complexe. Dans la pratique, on utilise le plus souvent des modèles élastoplastiques, qui donnent une relation entre contraintes et déformations qui est non linéaire, mais indépendante du temps. Les effets de fluage et de viscosité peuvent être pris en compte pour des applications particulières qui le nécessitent – et si on peut accéder expérimentalement aux paramètres correspondants – mais l’utilisation des modèles de ce type reste limitée.
Parmi les modèles élastoplastiques, on recourt encore le plus souvent aux modèles élastiques linéaires parfaitement plastiques (voir l’enquête citée par Gilleron, 2016). L’utilisation de modèles élastiques non linéaires associés à un ou plusieurs mécanismes plastiques écrouissables se généralise progressivement, en particulier sous l’impulsion des éditeurs de logiciels : ils donnent des résultats nettement plus représentatifs de la réalité dans certains cas (par exemple pour l’excavation devant une paroi moulée) mais l’on ne maîtrise pas forcément très bien l’influence de chacun des paramètres de ces modèles. De manière générale, le choix d’un modèle de comportement pour les sols doit tenir compte des objectifs fixés pour le calcul, du type d’ouvrage (et du type de sollicitation auquel le sol sera soumis), du niveau de précision des reconnaissances et des essais en laboratoire disponibles.
2) Etat initial
Pour les modèles non linéaires, la raideur du matériau dépend de l’état initial des contraintes dans le massif de sol étudié (et éventuellement d’autres paramètres, d’écrouissage ou d’endommagement par exemple). La détermination des contraintes initiales a donc une influence déterminante sur les résultats. Malheureusement, les contraintes initiales sont généralement évaluées de manière très simple : elles sont soit assimilées à un champ de contrainte « géostatique » (pour un massif dont la surface est horizontale), soit obtenues en appliquant la gravité à l’ensemble du maillage à partir d’un état de contraintes nul. Ces procédés sont relativement pauvres comparés à la complexité des modèles rhéologiques utilisés pour les sols. Ils restent cependant incontournables en pratique, faute d’un meilleur moyen d’estimer les contraintes initiales dans le sol.
$translationBooksF.3 Interactions sol-structure
F.3 Interactions sol-structure
Les ouvrages géotechniques associent souvent des couches de sol et des structures métalliques ou en béton, qui sont généralement beaucoup plus raides que le sol. L’interaction peut être limitée à quelques points d’appui de la structure sur le sol, ou être continue sur une surface significative, à l’extrados d’un tunnel, ou sur une paroi de soutènement.
L’interaction sera traitée de manière plus ou moins précise selon le cas.
Dans le cas des tunnels par exemple, on considère très couramment une adhérence parfaite entre le sol et la voûte d’un tunnel, en raison du mode de construction : avec les méthodes traditionnelles (séquentielles), le soutènement est constitué de béton projeté directement sur la surface de terrain découverte par l’excavation, ce qui assure en principe une bonne continuité du déplacement ; lors du creusement au tunnelier, on s’efforce d’assurer une bonne transmission des efforts entre le terrain et les voussoirs en procédant à des injections de bourrage pour remplir l’espace entre l’anneau et le terrain. Dans les tunnels anciens, les pathologies observées (ou des essais effectués dans le tunnel) peuvent cependant laisser penser que le contact est localement perdu entre la voûte et le terrain, par exemple à cause de circulations d’eau qui ont pu lessiver le terrain : la modélisation doit alors décrire de manière plus précise les conditions de contact entre le terrain et la voûte.
Les tunnels construits en tranchée couverte constituent un problème différent, dans la mesure où l’on remblaie le terrain autour de la structure. La modélisation de cette opération peut demander de prendre en compte explicitement, à l’aide d’éléments spécifiques, l’interface entre la voute et le sol.
Il est courant également d’introduire une modélisation explicite de l’interface entre le sol et la structure pour les soutènements, lorsqu’on remblaie derrière un mur (le phénomène de glissement du sol à l’interface avec la structure étant analogue à celui mis en jeu pour les tranchées couvertes), ou lorsqu’on excave devant une paroi moulée par exemple, le massif de sol soutenu pouvant glisser et présenter un déplacement vertical plus important que la tête de la paroi.
La question de la modélisation d’une interface entre les sols et les structures doit être examinée au cas par cas. On peut introduire des éléments de contact ou d’interface spécifiquement destinés à représenter l’interaction mécanique entre les deux, mais ces éléments introduisent de nouveaux paramètres, qui ne sont pas forcément simples à identifier (les raideurs normale et tangentielle de l’interface). Cette approche de modélisation présente un risque : les éléments d’interface tendent à contrôler le comportement de l’ouvrage et à estomper le rôle du comportement du sol, donnant l’impression que la réponse de l’ouvrage ne dépend pratiquement plus du sol.
Ouvrages renforcés
Dans de nombreux cas, le sol est renforcé par des inclusions présentant des caractéristiques de raideur et de résistance très élevées. Ces inclusions sont réparties de manière discrète dans le sol et très élancées : pieux, micropieux, tirants d’ancrage, armatures de murs en sol renforcé. Cette particularité géométrique pose différentes difficultés. En premier lieu, en toute rigueur, une file de pieux n’est pas équivalente à un mur continu, et l’utilisation de calculs en déformation plane n’est pas justifiée. En pratique, on est conduit à adopter, pour le mur du calcul plan, des caractéristiques mécaniques « équivalentes » à celles de la file de pieux, moyennant des hypothèses plus ou moins difficiles à justifier. Il en va de même pour les paramètres de l’interface mécanique entre le sol et les pieux / le mur. La difficulté est la même si l’on représente le mur par des éléments surfaciques ou par des éléments linéiques de type poutre.
Pour lever cette difficulté, on peut recourir à une modélisation tridimensionnelle. Mais, à cause des dimensions de la section des inclusions, il n’est pas possible de représenter dans le maillage la géométrie réelle des inclusions dès que leur nombre dépasse quelques unités : pour un mur en terre armée, avec des armatures de section 5 mm x 45 mm, à raison de 4 à 6 armatures par écaille de 0,75 m x 0,75 m, et pour un volume dont les dimensions sont de l’ordre de la dizaine de mètres, le nombre de nœuds d’un maillage qui respecterait la géométrie réelle des inclusions et qui donnerait une discrétisation acceptable dépasse les capacités de calcul actuelles. On peut donc proposer de représenter les inclusions par des éléments unidimensionnels (avec ou sans prise en compte des effets de flexion). Cette approche est critiquable au plan théorique, parce que l’introduction d’une densité linéique de force exercée par l’inclusion dans un milieu tridimensionnel n’est pas compatible avec la représentation classique des efforts intérieurs par un tenseur de contraintes. Elle est cependant utilisée, mais il faut être prudent dans l’interprétation des résultats, au moins pour ce qui concerne les contraintes au voisinage des inclusions.
Une solution alternative consiste à adopter des approches de type homogénéisation pour prendre en compte l’influence des inclusions sur le comportement global de l’ouvrage. Des modèles plus ou moins complexes ont été développés et implantés dans certains logiciels.
Quels que soient les choix effectués (calcul en déformation plane ou en condition tridimensionnelle, discrétisation des inclusions – par des éléments linéiques ou non – ou approche homogénéisée), il faut représenter l’interaction mécanique entre le pieu et le sol qui se produit au niveau du contact entre le sol et la paroi latérale du pieu, et aussi entre le sol et le pied du pieu. La modélisation de l’interaction mécanique au pied du pieu est particulièrement difficile à maîtriser. La modélisation d’un pieu unique par des éléments de volume, avec éventuellement des éléments d’interface avec le sol qui l’environne, donne des résultats qui dépendent du maillage et du modèle de comportement utilisé pour le sol. Il est, au minimum, nécessaire d’utiliser un modèle qui reproduit la rupture du sol en compression si l’on s’intéresse à la rupture du pieu. Les modèles de type Mohr Coulomb ou Drucker Prager, par exemple, ne sont pas adaptés dans ce contexte.
Dans certaines modélisations 2D ou 3D où les inclusions sont représentées par des éléments de barre ou de poutre, on associe à l’inclusion une extrémité fictive (par exemple un élément de poutre horizontal perpendiculaire au pieu), pour tenter de mieux représenter l’interaction en pied : il semble pour le moins indiqué de réaliser des études de sensibilité sur la dimension des éléments ajoutés pour vérifier la pertinence de cette approche.
Enfin, d’autres techniques de modélisation sont disponibles, qui proposent d’intégrer explicitement un modèle d’interaction pour le frottement latéral et un autre pour l’interaction de pointe via des éléments ad hoc.
Sans vouloir entrer davantage dans les détails, on attire donc l’attention de l’utilisateur sur le fait qu’il est amené à choisir entre des techniques de simulation numériques, et des modèles, qui ont une influence directe sur les résultats qu’il obtiendra.
$translationBooksF.4 Effets hydrauliques
F.4 Effets hydrauliques
1) Couplage hydromécanique
Une autre particularité des calculs géotechniques concerne le rôle de l’eau présente dans les sols. Lorsqu’on applique rapidement un chargement mécanique sur une couche de sol saturée, il se produit une déformation instantanée et une mise en pression du fluide au voisinage de la charge appliquée. En fonction des conditions aux limites hydrauliques, le gradient de la charge hydraulique provoque une mise en mouvement du fluide, qui conduit à une redistribution de la pression et à déformation différée du sol.
On a donc à traiter un problème de couplage hydromécanique. Un cadre théorique solide a été établi par Biot (1941) et développé par Coussy (1991). Sur le plan de la résolution numérique, le problème couplé est nettement plus délicat à traiter qu’un problème classique, pour plusieurs raisons :
-
le problème comporte, en plus des déplacements, un nouveau champ inconnu, le champ de pression de l’eau,
-
il faut préciser des conditions aux limites spécifiques au problème hydraulique (définir les parties du contour qui sont imperméables et celles où la pression est imposée),
-
la solution (en déplacement et en pression) dépend du temps,
-
la nature mathématique du problème à résoudre est différente,
-
il faut décrire de manière quantitative la perméabilité des différentes couches de sol.
Le traitement complet du couplage hydromécanique est rarement effectué. On tente généralement de se limiter à une approche découplée du problème, dans laquelle on calcule l’évolution du champ de pression en négligeant les déformations du solide, mais ce découplage a pour conséquence de sous-estimer fortement la durée sur laquelle la redistribution de pression se produit.
2) Sols non saturés
Le traitement des sols non saturés complique encore le problème, la transition entre les zones quasi-saturées et les zones non saturées introduisant des inconnues, des non linéarités et des paramètres supplémentaires. A nouveau, le traitement complet des sols non saturés reste rare. On préfère proposer des solutions simplifiées, en négligeant les zones partiellement saturées par exemple.
La question de l’état initial dans le cas des sols non saturés est extrêmement délicate, faute de moyens expérimentaux permettant de le caractériser in situ.
$translationBooksF.5 Incertitudes et recommandations
F.5 Incertitudes et recommandations
1) Incertitudes
Les sources d’incertitude sont nombreuses en géotechnique. La première réside dans la relative méconnaissance de la géométrie des couches de sol constituant le massif étudié. Outre la connaissance de la géologie de la région où est implanté l’ouvrage étudié, les principales sources d’information sont les sondages effectués sur le site du projet. L’extrapolation entre les sondages, surtout s’ils sont éloignés les uns des autres et pas localisés précisément à l’emplacement de l’implantation définitive de l’ouvrage (qui peut être modifiée après les reconnaissances, par exemple dans le cas des tunnels), ne donne pas nécessairement une représentation exacte des variations locales d’épaisseurs des couches.
En zone urbaine, la présence d’hétérogénéités (caves, puits, fondations d’ouvrages antérieurs) est souvent difficile à détecter.
L’autre source d’incertitude, déjà évoquée, concerne l’état initial des contraintes (et des pressions interstitielles éventuellement) dans le massif de sol. Elle peut avoir une influence majeure sur les résultats du calcul : c’est particulièrement clair dans le cas des tunnels, où les chargements pris en compte dépendent des contraintes initiales.
Enfin, le choix des modèles de comportement et la détermination des paramètres de ces modèles introduisent une incertitude importante sur la représentativité des calculs : si le modèle de comportement ne capte pas un phénomène qui contrôle le comportement de l’ouvrage, le résultat peut être qualitativement et quantitativement très éloigné de la réalité.
2) Recommandations
De manière générale, l’utilisateur doit être conscient des objectifs du calcul qu’il entreprend : la démarche est différente selon qu’on cherche à justifier un dimensionnement ou à évaluer l’influence de certaines dispositions constructives (le nombre et la position des butons par exemple).
Il faut également être conscient des choix de modélisation sur lesquels le calcul repose (même si ces choix sont parfois en partie imposés par le logiciel qu’on utilise). Il faut en particulier être en mesure d’identifier les phénomènes à prendre en compte, ce qui conduit à choisir une analyse quasi-statique ou dynamique, avec ou sans prise en compte du couplage hydromécanique, etc.
Il convient de choisir entre un calcul 2D et un calcul 3D. Les calculs tridimensionnels restent pour le moment rares, à cause du temps de préparation des calculs. Pour certains problèmes, cependant, il ne fait pas de doute que des calculs bidimensionnels ne peuvent donner qu’une indication très pauvre du comportement de l’ouvrage étudié, quel que soit le soin apporté à la détermination des paramètres de sol. Ainsi par exemple, l’étude de la stabilité du front de taille d’un tunnel ne peut pas vraiment être envisagée en dehors d’un contexte tridimensionnel. Il en va de même pour l’étude du renforcement du front de taille d’un tunnel par des boulons. Le développement de pré-processeurs dédiés à des applications particulières devrait permettre de recourir plus facilement à des calculs tridimensionnels et améliorer la représentativité de nombreuses analyses par éléments finis.
En géotechnique, le choix des paramètres de sol doit faire l’objet d’une attention particulière : il pourrait faire l’objet d’un livre entier. La plupart des modèles de comportement évolués ne s’accompagnent pas d’une procédure d’identification des paramètres détaillée et robuste, principalement parce qu’on ne sait pas résoudre les équations du modèle même pour un problème simple comme celui de la compression à l’appareil triaxial. On est donc amené à caler les paramètres en faisant en sorte que la modélisation d’essais triaxiaux par exemple donne des résultats en accord satisfaisant avec les résultats d’essais qu’on peut avoir. On procède par tâtonnements, et l’accord obtenu étant évalué de manière subjective (parce qu’on peut choisir de mieux reproduire une partie ou une autre des courbes expérimentales), il n’est pas garanti que deux utilisateurs retiennent les mêmes valeurs des paramètres à partir des mêmes essais. De ce point de vue, tous les modèles de comportement n’ont pas les mêmes qualités : certains disposent d’un grand nombre de paramètres qui ont chacun une influence sur un aspect particulier de la réponse du sol (mais qui n’apparait pas forcément dans les résultats d’essais dont on dispose) ; d’autres modèles ont au contraire un nombre relativement réduit de paramètres, mais chacun d’eux peut modifier simultanément plusieurs aspects de la déformabilité du sol : cela ne facilite pas le calage.
La dernière recommandation que l’on doit absolument garder à l’esprit est que l’utilisateur doit vérifier autant que possible son calcul. Il n’existe pas encore d’outils généraux pour mesurer la qualité d’un calcul : des travaux de recherche visent à fournir des estimateurs d’erreur a posteriori mais leur utilisation en géotechnique reste rare. Il est donc nécessaire de regarder en détail les résultats du calcul : certaines incohérences sont parfois faciles à détecter. En cas de doute, il est utile de faire contrôler ses résultats par un œil extérieur. En tout état de cause, il est vivement indiqué de réaliser des études paramétriques pour se faire une idée de l’influence de certains facteurs, en particulier des paramètres de sol, si l’on n’est pas certain que leur influence sur les résultats est modérée et qu’on a pu déterminer leur valeur avec une précision acceptable.
$translationBooksF.6 Aspects normatifs : Principes de l'Eurocode 7
F.6 Aspects normatifs : Principes de l'Eurocode 7
La modélisation numérique a toujours eu un lien particulier avec les normes de calcul qui se focalisent essentiellement sur la vérification d’états limites ultimes avec le calcul d’un coefficient de sécurité ou d’un équilibre de forces intégrant des coefficients partiels. En effet, la modélisation numérique fournit avant toute chose des valeurs de déplacements et de déformations et est donc un outil très adapté à la vérification des états limites de service (ELS) pour lesquels les coefficients partiels sont égaux à 1,0. Son utilisation pour la vérification des états limites ultimes (ELU) a donc paru limitée dans un premier temps.
Désormais, notamment avec les procédures de réduction des propriétés de cisaillement des terrains (par exemple, la procédure de type « c-phi reduction »), il est aisé de calculer un coefficient de sécurité. Il est aussi possible, à travers les procédures suggérées par certaines normes de calcul, notamment l’Eurocode 7, de considérer les résultats d’une modélisation numérique tant pour la vérification des états limites ultimes que pour celle des états limites de service.
L’Eurocode 7 dans sa version actuelle n’est toutefois pas forcément très clair quant à l’analyse et l’exploitation des résultats issus d’une modélisation numérique. En effet, les trois approches de calcul proposées par l’Eurocode 7 qui permettent d’appliquer des coefficients partiels sur les actions, les effets des actions (moments fléchissants et efforts tranchants dans un écran de soutènement, effort axial dans un pieu, etc.), les propriétés des terrains (c et ou cU) et les résistances géotechniques ont été pensées pour être utilisées avec des méthodes d’équilibre limite.
Les vérifications liées à l’application des Eurocodes sont principalement transcrites sous la forme de comparaisons entre des actions ou des effets des actions et des résistances. Néanmoins, un certain nombre de publications (Potts et Zdravkovic, 2012, Tschuchnigg et al., 2015, etc.) et les compte rendus de différents groupes de travail réunis en vue de la mise au point de la seconde génération des Eurocodes permettent d’esquisser des procédures de vérifications. En premier lieu, il est important de souligner que la pondération « à la source » des propriétés des sols ou des roches, c'est-à-dire la possibilité de réduire la cohésion et l’angle de frottement avant de réaliser le calcul n’est pas admise car elle conduit à générer des résultats qui ne peuvent pas être interprétés. Différentes procédures sont toutefois utilisables et sont synthétisés dans le tableau ci-dessous.
Synthèse des différentes types de vérifications aux ELU
| Type de vérifications aux ELU | 1 – ELU structurels | 2 – ELU géotechniques (et structurels) | 3 – ELU géotechniques | 4 - ELU structurels (et géotechniques) |
|---|---|---|---|---|
| Type de procédures | Multiplication des effets des actions par 1,35 | Réduction des propriétés de cisaillement des terrains | Estimation de la résistance mobilisée autour d’un ouvrage géotechnique spécifique (pieu, tirant, etc.) | Augmentation des charges appliquées sur l’ouvrage géotechnique |
| Commentaires | A combiner avec la vérification des ELU géotechniques | A combiner avec la vérification des ELU structurels | A combiner avec la vérification des ELU structurels | A priori, cette approche se suffit à elle-même |
L’approche qui tend à s’imposer consiste à réaliser un calcul avec des valeurs caractéristiques tant pour les charges que pour les propriétés des terrains pour atteindre un premier état d’équilibre. Par rapport à cet état d’équilibre, deux types de vérifications sont à réaliser. La première de type 1 est relative aux ELU structurels et consiste à multiplier les effets des actions calculés par 1,35 (c'est-à-dire le coefficient habituellement considéré dans les Eurocodes pour les charges permanentes défavorables). La seconde de type 2 est relative aux ELU géotechniques et consiste à réduire de manière progressive les propriétés de résistance au cisaillement des terrains modélisés pour mettre en évidence un mécanisme de rupture. Le facteur de réduction appliqué peut être considéré comme un coefficient de sécurité mais son interprétation peut être sujette à discussion. En effet, lors de la réduction de propriétés de cisaillement, différents éléments peuvent interagir comme les fonctions d’écrouissage ou les règles d’écoulement. Dans le cas de calculs associant des éléments volumiques et des éléments de structure de type « barre » ou « poutre », cette vérification peut aussi être utilisée pour vérifier les ELU structurels. En effet, les déplacements accumulés au cours de la procédure de réduction des propriétés de résistance au cisaillement engendrent des efforts dans les éléments de structure dont l’interprétation n’est pas complètement partagée par l’ensemble des chercheurs ou ingénieurs. L’utilisateur doit donc être très prudent sur la manière donc ce type de procédures est implémenté. La figure 7.1 présente comment s’enchaînent les vérifications de type 1 et 3 dans le cas d’un calcul phasé.
Les ELU géotechniques peuvent être aussi appréhendés de manière spécifique en considérant la résistance mobilisée autour de l’ouvrage géotechnique à dimensionner, un pieu, un tirant d’ancrage, etc. et à la comparer à la résistance mobilisable fournie par l’application des normes, par exemple, les règles pressiométriques pour le calcul de la portance des pieux : c’est la procédure de type 3 et elle doit forcément être associée à la procédure de type 1 en ce qui concerne les ELU structurels.
Dans certaines configurations, notamment des pieux ou des semelles, il est aussi possible de faire croître les actions appliquées sur l’ouvrage géotechnique à dimensionner pour directement obtenir l’effort maximal applicable et en déduire un coefficient de sécurité : c’est l’objet de l’approche de type 4.
De manière plus générale, les méthodes permettant de justifier les ELU géotechniques doivent permettre, soit de déterminer un mécanisme de rupture et de vérifier que l’on dispose de suffisamment de marge vis-à-vis du déclenchement de ce mécanisme (c’est l’objet des vérifications de type 2 et 4), soit de comparer la résistance mobilisée à une résistance mobilisable que l’on peut calculer par ailleurs (c’est l’objet de la vérification de type 3).

Enchaînement des vérifications aux ELU dans un calcul phasé
Quand le mécanisme de rupture est associé à l’action de l’eau alors des précautions particulières sont à prendre. En effet, les procédures décrites précédemment ne permettent pas correctement de calculer un coefficient de sécurité si le mécanisme de rupture résulte exclusivement de l’action de l’eau. En premier lieu, il faut définir si le mécanisme de rupture est lié à un défaut d’équilibre mécanique (par exemple, un niveau trop haut en arrière d’un écran de soutènement) ou à un problème hydraulique (par exemple, un gradient hydraulique trop élevé).
Dans le cas d’un défaut d’équilibre mécanique, il est nécessaire de réaliser une étude paramétrique relative au niveau de la nappe de manière à pouvoir estimer son effet en mettant en œuvre les vérifications aux ELU présentées dans le tableau précédent. Dans le cas d’un problème hydraulique, il est possible de comparer le gradient calculé à un gradient critique calculé par ailleurs et aussi de vérifier que les contraintes effectives restent positives en tout point du massif (la condition sur le gradient critique étant plus conservatrice que la condition sur la contrainte effective).
F.7 Modélisation en dynamique
F.7 Modélisation en dynamique
A cause de la nature continue et non-confinée des géomatériaux, le traitement des problèmes dynamiques dans le milieu « sol » diffère essentiellement du traitement des problèmes dynamiques associés aux structures classiques du génie civil. Alors que pour la plupart de ces dernières une modélisation mécanique, par le biais d’un assemblage de masses et de sources de rigidité discrètes, suffit a priori pour appréhender leur comportement dynamique, les géomatériaux doivent être traités en tant que milieux continus et non-bornés et leur réponse dynamique doit être étudiée dans le contexte des problèmes mécaniques de la propagation d’ondes.
Concernant les méthodes numériques employées en dynamiques des sols, il convient d’abord de noter que la modélisation de la propagation d’ondes nécessite de faire appel à une palette de méthodes de modélisation et de calcul, qui diffèrent des calculs géotechniques conventionnels par la méthode des éléments finis. Bien que cette dernière occupe une place importante dans l’inventaire de méthodes à la disposition de l’ingénieur pour les problèmes de dynamique des sols, elle est souvent couplée ou remplacée par d’autres méthodes de calcul numérique, mieux adaptées pour modéliser la propagation d’ondes dans des milieux non-bornés.
En outre, les équations qui décrivent les problèmes dynamiques font intervenir une nouvelle variable (en dehors des variables spatiales) : celle du temps. Les schémas de résolution sont formulés dans le domaine temporel, et alternativement, dans le domaine fréquentiel. Les méthodes pour les problèmes en dynamique des sols sont implémentées dans des logiciels dédiés, nécessitant à la fois une très bonne maîtrise des notions théoriques de base et aussi un savoir-faire ciblé pour ce qui est de la définition des paramètres, du calage des modèles numériques et des lois constitutives, de l’optimisation des calculs etc.
Parmi les problèmes courants de la dynamique des sols, on peut citer :
-
l’étude des vibrations dans le sol à cause de la construction (par exemple lors du battage de pieux) ;
-
l’étude de la réponse des sols à cause du comportement vibratoire des structures (machines tournantes, vibrations à cause des effets du vent, isolation et réduction des effets vibratoires d’équipements etc.) ;
-
les vibrations engendrées par les chocs, les impacts, les explosions ;
-
les vibrations à cause des charges mobiles, en particulier les charges de trafic ;
-
la réponse sismique des géomatériaux et la propagation sismique des ondes dans le milieu sol, avec la caractérisation du mouvement sismique pour la conception parasismique des ouvrages ;
-
l’interaction sol-structure et la prise en compte de l’enfoncement (le cas échéant) dans la réponse dynamique des structures ;
-
le calcul des fonctions d’impédances de systèmes de fondations ;
-
la caractérisation du comportement cyclique des sols et le développement de lois constitutives adaptées ;
-
la vérification de la stabilité sismique des ouvrages géotechniques (fondations, ouvrages en terre, ouvrages de soutènement, ouvrages souterrains) ;
-
la modélisation du couplage avec la phase fluide dans le sol (liquéfaction) etc.
F.8 Échelles caractéristiques
F.8 Échelles caractéristiques
Pour cadrer la discussion concernant les problèmes de la dynamique de sols, il faut d’abord faire la distinction parmi les échelles caractéristiques relatives à la définition des phénomènes physiques étudiés dans ces problèmes. Ces échelles sont :
-
l’échelle géologique,
-
l’échelle de site,
-
l’échelle géotechnique,
-
l’échelle de la structure génie civil.
Chaque problème en dynamique de sols fait intervenir une ou plusieurs de ces échelles, ce qui constitue déjà une première difficulté, car il faut associer dans un même modèle, des domaines dont les dimensions sont très différentes.
Le passage d’une échelle à une autre correspond à un type de problème spécifique, nécessitant des approches de résolution qui lui sont propres. Ainsi, dans le contexte des problèmes sismiques par exemple, le passage de l’échelle géologique à l’échelle de site donne lieu au problème de la détermination des effets locaux de site. Le passage à l’échelle géotechnique donne lieu au problème de la caractérisation du mouvement sismique en un point de contrôle (qui peut être localisé en surface du sol ou à une profondeur caractéristique). Enfin, le passage à l’échelle de la structure donne lieu au problème de l’interaction sol-structure, c’est-à-dire au problème de déterminer comment la réponse dynamique du sol est modifiée par la présence de la structure et vice versa.
Selon le problème étudié, il est également possible que l’échelle de la structure interagisse directement avec l’échelle de site ou l’échelle géologique. Ceci est surtout vrai pour les structures de grandes dimensions, telles que les ponts (échelle de structure ~ échelle de site) ou les tunnels (échelle de structure ~ échelle géologique).
Dans la suite, il convient de limiter la discussion sur les échelles géotechnique et de la structure (échelles caractéristiques pour la majorité des structures du génie civil) et donc se concentrer aux problèmes d’Interaction Dynamique Sol-Structure (IDSS).
1) Classification des méthodes pour l’IDSS
Pour proposer une classification des méthodes pour l’IDSS, on notera d’abord que les systèmes dont le comportement dynamique est étudié, sont constitués des deux domaines distincts :
-
le domaine de la structure, comportant l’ouvrage étudié et éventuellement une zone de sol au voisinage de cet ouvrage : ce domaine met en évidence des dimensions bornées. Il est couramment appelé domaine de structure généralisée ou superstructure ou tout simplement structure ;
-
le domaine de sol, entourant cette structure, dont les dimensions sont non-bornées.
Les deux domaines sont séparés par une frontière qui est appelée horizon d’interaction. Cette frontière est bien évidemment fictive et sa définition est, dans un certain sens, arbitraire. Par exemple, l’horizon d’interaction peut être identifié avec la vraie interface entre la structure et le sol, ou être placée très loin de la structure.
Par ailleurs, puisque le problème d’IDSS résulte en un problème de propagation d’ondes, la formulation adoptée doit satisfaire une condition de radiation. Par exemple, dans le cas d’un chargement appliqué sur la structure (c’est-à-dire que la structure est identifiée comme la source des ondes), la condition de radiation exige qu’il ne puisse pas y avoir d’ondes convergeant vers la source.
Les méthodes pour l’IDSS sont divisées en trois grandes familles :
-
méthodes de sous-structures,
-
méthodes directes,
-
méthodes hybrides.
Les méthodes de sous-structures sont les plus courantes dans les études d’IDSS en Génie Civil. L’horizon d’interaction dans ce cas est placé au niveau de l’interface physique entre le sol et la structure. Cette séparation permet de modéliser le domaine « structure » par des éléments finis classiques et le domaine « sol » par d’autres approches, mieux adaptées pour le traitement de domaines non-bornés, en particulier par la méthode des éléments de frontière (BEM ou une de ses variantes). La condition de radiation est formulée de manière rigoureuse à l’infini. La méthode de sous-structures acquiert son intérêt pratique, si elle est combinée avec l’hypothèse de linéarité de comportement pour les domaines « structure » et « sol ». Dans ce cas, il peut être montré, via le théorème de superposition de Kausel, que le problème global d’interaction sol-structure peut être décomposé en trois sous-problèmes, comme présenté sur la figure ci-dessous.

Théorème de superposition de Kausel dans la méthode de sous-structures
L’interaction cinématique concerne la diffraction des ondes dans le sol par la présence de la fondation et le chargement conséquent de cette dernière. L’interaction inertielle concerne l’échange d’énergie entre le sol et la structure qui peut être caractérisé en termes d’impédance. Ces deux premiers problèmes fournissent respectivement, le mouvement d’entrainement et les conditions aux limites qui peuvent être utilisés, dans le troisième sous-problème, pour l’analyse dynamique du domaine borné. Par conséquent, dans la méthode des sous-structures, l’utilisation des éléments finis n’intervient essentiellement que dans la modélisation de la structure ; on peut donc se référer directement aux chapitres concernant l’utilisation des éléments finis dans les études conventionnelles en dynamique des structures.
Un des inconvénients, quant à l’utilisation du théorème de superposition de Kausel, est lié à la nature des géomatériaux, qui présentent d’emblée un comportement mécanique (fortement) non-linéaire. Ainsi, pour pouvoir faire appel à l’hypothèse de linéarité de comportement pour le domaine « sol », il est nécessaire de procéder à un calage des paramètres viscoélastiques des géomatériaux, en conformité avec les niveaux des déformations qui y sont anticipés. La définition des paramètres viscoélastiques effectifs des couches de sol constitue la première étape pour la mise en œuvre de la méthode de sous-structures et permet l’utilisation du théorème de superposition dans des systèmes où le comportement non-linéaire reste modéré.
Les méthodes directes constituent la deuxième grande famille d’approches pour l’IDSS et sont surtout applicables pour les systèmes qui présentent de fortes non-linéarités de comportement. L’horizon d’interaction dans ce cas est placé très loin de la structure, englobant une grosse zone du domaine « sol », comme présenté sur la figure ci-dessous.

Principe général des méthodes directes
L’équation d’équilibre dynamique est formulée pour l’ensemble « structure + sol » et fait intervenir un vecteur de chargement extérieur qf, défini le long de l’horizon d’interaction. L’ensemble « structure + sol » est modélisé par la méthode en éléments finis et les déplacements dans les domaines « sol » et « structure » sont calculés simultanément. La résolution est effectuée dans le domaine temporel. Il est alors possible d’incorporer dans le modèle toutes les caractéristiques géométriques du problème, les hétérogénéités matérielles du sol ou de la superstructure et d’introduire les lois de comportement nécessaires pour la description des non-linéarités du système. En dépit de ces importants avantages, les méthodes directes mettent en évidence plusieurs points délicats :
-
la définition de la position optimale pour l’horizon d’interaction et la détermination du chargement extérieur à y introduire (surtout pour les problèmes sismiques) sont des tâches non triviales, nécessitant souvent un travail préparatoire conséquent ;
-
à l’opposé des méthodes des sous-structures, où la condition de radiation est formulée de manière rigoureuse à l’infini, dans les méthodes directes, la condition de radiation est formulée de manière approchée au niveau de l’horizon d’interaction. Cette hypothèse permet de s’affranchir de la modélisation du domaine non-borné, mais crée le besoin d’utilisation d’éléments spéciaux le long de l’horizon d’interaction (qui est identifié avec la frontière du domaine modélisé) ; ces éléments sont censés préserver le caractère non-borné du domaine modélisé en garantissant qu’il n’y aura pas de réflexions d’ondes parasites le long de la frontière du domaine modélisé ;
-
les discrétisations spatiale et temporelle (taille de mailles, pas de temps) dépendent des paramètres mécaniques du système modélisé et souvent la taille de mailles ou le pas de temps qui sont nécessaire pour un problème, peuvent s’avérer prohibitifs vis-à-vis du coût de calcul ;
-
le schéma d’intégration temporelle doit satisfaire les exigences de précision et de stabilité de la solution, tout en restant optimisé par rapport au coût calculatoire ;
-
les lois de comportement adoptées pour décrire le comportement non-linéaire des sols nécessitent un calage pour pouvoir bien représenter le comportement cyclique des sols ;
-
enfin, les méthodes directes restent encore extrêmement coûteuses pour des problèmes 3D. Il est donc nécessaire souvent de pouvoir faire le passage du comportement 3D à une modélisation 2D tout en préservant les caractéristiques dynamiques (masse / rigidité / caractéristiques modales) du système étudié.
Enfin, les méthodes hybrides forment la troisième grande famille de méthodes pour le traitement de l’IDSS. Ces méthodes sont situées entre les méthodes directes et les méthodes de sous-structures ; l’idée principale consiste à séparer le sol dans deux domaines distincts : le premier est un champ proche de la structure où l’on suppose que toutes les non-linéarités pertinentes pour le problème de l’IDSS sont développées. Le deuxième est le champ lointain où le comportement du sol n’est pas affecté par l’interaction avec la structure. Ainsi, le champ lointain peut être traité par les techniques adaptées pour les problèmes linéaires dans des domaines non-bornés (typiquement BEM avec une résolution dans le domaine fréquentiel), alors que le champ proche est incorporé dans le modèle de la superstructure et peut être traité par une méthode directe (modélisation par éléments finis – modélisation des non-linéarités – résolution dans le domaine temporel). Le principe général des méthodes hybrides est présenté sur la figure ci-dessous.

Principe général des méthodes hybrides
Le point délicat des méthodes hybrides est la définition de la frontière entre le champ proche et le champ lointain (horizon d’interaction) ainsi que la formulation d’un schéma qui permet de restituer de manière rigoureuse mais efficace le couplage entre les deux champs. Au plan numérique, cette opération résulte typiquement en un schéma de couplage FEM-BEM, où la composante BEM alimente la composante FEM avec les historiques des forces d’interaction et les fonctions d’impédances à déployer le long de l’horizon d’interaction.
Un cas particulier de modélisation appartenant aux méthodes hybrides concerne le développement de macroéléments pour la modélisation du comportement dynamique non-linéaire de différents types de fondations. Les macroéléments sont des éléments de liaison, qui sont situés au niveau de la fondation et qui sont dotés d’une loi de comportement permettant de décrire les mécanismes non-linéaires développés le long des interfaces sol-structure, tels que le glissement, le décollement et la plastification du sol.
Les points précédents laissent entendre qu’au sein des approches pour l’IDSS, la méthode aux éléments finis est surtout utilisée dans la famille des méthodes directes et aussi dans la famille des méthodes hybrides pour la modélisation du champ proche.
Dans les paragraphes suivants, on donne quelques indications sur la méthode de sous-structuration et on discute quelques points délicats quant à l’implémentation des méthodes directes pour les problèmes d’IDSS.
2) Compléments sur la méthode de sous-structuration
La première étape de la méthode de sous-structuration est le calage des paramètres viscoélastiques des géomatériaux en fonction du niveau des déformations. Le comportement non-linéaire hystérétique d’un sol sous sollicitations cycliques peut être approximé par un module de cisaillement et un amortissement visqueux équivalents. D’abord il faut définir les courbes de la réduction du module de cisaillement et de l’augmentation du coefficient d’amortissement en fonction de la déformation sur la base de résultats d’essais de laboratoire dédiés au projet (partie des reconnaissances géotechniques) ou, en l’absence d’une campagne géotechnique dédiée, sur la base de références scientifiques.
Puis, une analyse unidimensionnelle linéaire de la réponse d’une colonne de sol est à conduire à l’aide des fonctions de transfert qui, à partir de l’accélération au rocher et d’un premier jeu des propriétés des couches de sol, donnent les déplacements, les vitesses, les accélérations, les contraintes et les déformations en cisaillement dans chaque couche. Enfin, une procédure itérative est nécessaire afin d’assurer que les propriétés utilisées dans l’analyse sont compatibles avec les déformations maximales calculées dans les couches.
L’analyse inverse, soit le calcul du mouvement au rocher à partir de l’accélération en surface, est possible à travers les mêmes fonctions de transfert et prend le nom de déconvolution. La procédure itérative ne garantit pas toujours l’unicité de la solution dans la recherche des propriétés équivalentes du sol en cas des larges déformations. Ces analyses peuvent être menées avec des logiciels dédiés comme SHAKE 91 par exemple.
Les problèmes de diffraction et d’impédance peuvent être résolus dans le domaine fréquentiel par des outils de calculs adaptés, tel que les codes SASSI2010 ou MISS3D. Des méthodes simplifiées valables sous certaines conditions peuvent être utilisées, en alternative.
L’étude de l’interaction cinématique n’est d’intérêt que dans le cas de fondations profondes et est négligée dans le cas de fondations superficielles. Pour une analyse sismique, la méthode simplifiée consiste en l’imposition des déformations de sol en champ libre aux pieux de fondation. Cette sollicitation, d’origine cinématique, doit être additionnée aux sollicitations provenant de l’interaction inertielle pour le dimensionnement des pieux.
En utilisant un logiciel dédié (eg. SASSI2010, MISS3D), l’étude de l’interaction inertielle conduit au calcul de la raideur et de l’amortissement au point de contrôle de la fondation en fonction de la fréquence. Pour le calcul des fonctions d’impédance, la fondation est par défaut considérée comme une sous-structure rigide. Pour une fondation superficielle, les termes d’impédance relatifs aux déplacements et aux rotations sont retenus, tandis que pour une fondation profonde il faut prendre en compte aussi les termes de couplage entre les raideurs en déplacements et en rotations. Les valeurs des impédances, retenues pour le problème structurel d’analyse dynamique, sont calées sur la base des modes propres d’interaction sol-structure avec une procédure itérative expliquée ci-après. Une première analyse modale est conduite avec un jeu des valeurs d’impédance d’essai. Le jeu des valeurs d’impédance suivant est calculé à partir des fréquences des modes propres, identifiés comme ceux d’interaction sol-structure pour chaque degré de liberté de la fondation (supposée rigide). La deuxième analyse modale permet de corriger les fréquences des modes propres retenus et ainsi de suite. La procédure s’arrête lorsqu’on atteint la convergence des fréquences propres.
Les méthodes simplifiées pour les fondations superficielles, en général, donnent des formules pour le calcul direct de l’impédance. Les méthodes les plus connues sont celles de Newmark-Rosenblueth, de Deleuze, de l’Eurocode 7, du guide SETRA, de Veletsos et de Gazetas.
La condition principale pour la validité des méthodes simplifiées est l’hypothèse de sol homogène, monocouche, à l’exception de la méthode de Gazetas permettant la prise en compte d’un sol double-couche pour les cas des fondations de forme approximable à la forme circulaire. La méthode de Deleuze tient compte de la fréquence du mode de vibration fondamental de l’ouvrage. Les méthodes de Veletsos et Gazeats considèrent l’encastrement de la fondation dans le sol.
Pour les fondations profondes, la méthode de Gazetas et celle de l’Eurocode 8-5 donnent des formules applicables dans les trois conditions de sol suivantes :
-
sol dont le module de Young varie linéairement avec la profondeur ;
-
sol dont le module de Young varie avec la racine carrée de la profondeur ;
-
sol dont le module de Young reste constant avec la profondeur.
Une autre méthode simplifiée pour les fondations profondes est celle de Winkler nécessitant la modélisation d’une poutre reposant sur un système de ressorts et d’amortisseurs, calés sur la base des propriétés de chaque couche et représentant les pressions frontales et les efforts de frottement.
Suite à la résolution du problème d’analyse dynamique, la méthode de Winkler est utilisée aussi pour le calcul des sollicitations le long des pieux pour leur dimensionnement. Cette méthode permet de modéliser un comportement élasto-plastique pour chaque couche de sol et l’intégration d’une analyse simplifiée de l’interaction cinématique par application des déplacements de sol imposés au pieu.
3) Définition de la taille des mailles et du pas de temps
Le choix de la taille de mailles constitue une étape très importante dans la modélisation en dynamique des sols, puisque la finesse de discrétisation conditionne les caractéristiques des ondes qui peuvent être modélisées avec un maillage donné. Le critère habituel pour pouvoir modéliser avec une précision adéquate une onde se propageant dans le milieu sol, est de posséder dans le maillage, 10 mailles par longueur d’onde. Si on désigne par h la taille de mailles et par λ, la longueur d’onde, le critère à imposer sur la finesse de discrétisation s’écrit comme suit :

Ce critère peut encore être formulé en fonction de la vitesse de propagation minimale Vmin à prendre en compte dans le modèle et de la fréquence caractéristique maximale fmax des ondes à représenter dans le maillage. Le critère pour la taille de mailles s’écrit alors :

Pour les problèmes sismiques, la quantité Vmin correspond habituellement à la valeur minimale des vitesses effectives (compatibles avec le niveau sismique) de propagation d’ondes S pour les couches de sol modélisées. La quantité fmax correspond à la fréquence de coupure du spectre de dimensionnement (~30 Hz) ou à une fréquence maximale d’intérêt pour l’interaction sol-structure (~15 Hz).
En dehors de la taille de mailles h, le choix d’un pas de temps Δt est également conditionné par les caractéristiques mécaniques du milieu modélisé. En particulier, par analogie avec la longueur d’onde, il est nécessaire de pouvoir décrire la plus faible période propre à prendre en compte dans les analyses par au moins 10 incréments de temps (le critère de précision est identique dans les discrétisations spatiale et temporelle). Le critère sur le pas de temps peut être formulé comme suit :

où Vmax est la vitesse correspondant à valeur maximale des vitesses (effectives) de propagation des ondes S et h correspond à la taille de mailles.
A titre indicatif, dans une application avec Vmin = 150 m/s, Vmax = 500 m/s et fmax = 15 Hz, on aurait obtenu h ≤ 1 m et Δt ≤ 0,002 s. Une attention particulière doit être portée aux problèmes dynamiques non-linéaires, car les caractéristiques d’intérêt pour la définition de la taille de maille (en particulier V_min) évoluent avec le temps (assouplissement du sol en passant en régime élastoplastique).
4) Comportement cyclique des sols - Amortissement
On a vu que le grand intérêt pour la mise en œuvre des méthodes directes pour l’IDSS concerne la possibilité de modéliser rigoureusement le comportement non-linéaire des géomatériaux, au moins à l’intérieur du domaine englobé par l’horizon d’interaction, qui est modélisé en éléments finis. Le concepteur peut modéliser avec précision la géométrie des couches de sol et affecter à chaque formation, la loi de comportement la plus adaptée pour pouvoir reproduire le comportement cyclique anticipé.
Calage des modèles non-linéaires - La première étape dans cette procédure de modélisation concerne le calage de paramètres numériques intervenant dans la définition des lois constitutives choisies, de manière à que ces lois reproduisent avec précision le comportement cyclique des sols ; le comportement cyclique est d’emblée caractérisé, dans la majorité d’applications en Génie Civil, via la courbe de dégradation du module de cisaillement G en fonction de la distorsion γ (courbe G~γ). Il est rappelé que la courbe G~γ varie selon le type de sol (sable/argile/silt/gravier), la contrainte verticale effective, l’indice de plasticité etc. La procédure du calage des modèles non-linéaires intègre les étapes suivantes :
-
organisation du maillage faisant apparaître des zones régies par la même courbe G~γ ;
-
définition des paramètres élastiques (paramètres à faibles distorsions) pour chaque zone ;
-
adoption d’une loi constitutive adaptée pour chaque zone (surface de rupture, loi d’écrouissage, loi d’écoulement, comportement dans le plan déviatorique et dans l’axe hydrostatique etc.) ;
-
définition de la courbe G~γ caractérisant chaque zone en fonction -entre autres- de la contrainte moyenne effective dans la zone ;
-
calage des paramètres numériques caractérisant la loi de comportement non-linéaire de manière à reproduire la courbe G~γ de chaque zone.
La procédure du calage résulte en un tableau fournissant pour chaque zone, le type de loi constitutive adoptée et l’ensemble des paramètres numériques, nécessaires pour sa définition.
Comportement drainé et non-drainé - Dans le cas de la présence d’une nappe phréatique dans le domaine de sol, il est important de pouvoir définir si la réponse des géomatériaux lors de la sollicitation dynamique sera régie par un comportement en conditions drainées ou non-drainées. Cette définition dépend de la nature des sols (matériaux cohésifs ; matériaux pulvérulents) mais également de la durée du phénomène étudié. Pour les phénomènes dont la durée est limitée (de l’ordre de quelques secondes, y compris les séismes) il est souvent difficile de prescrire si le sol répondra en conditions drainées ou non-drainées. Pour ces situations, il est conseillé de mener deux calculs séparés, à la fois sous l’hypothèse de comportement drainé et non-drainé, et de définir la réponse globale via l’enveloppe de ces deux calculs.
Amortissement - Quand il s’agit de modéliser le comportement des couches de sol via une loi élastoplastique, l’amortissement matériel anticipé est obtenu directement via la dissipation qui résulte de la loi de comportement. Or, cette définition de l’amortissement diffère de la caractérisation conventionnelle de l’amortissement (accompagnant habituellement les définitions des courbes G-γ) via une courbe β-γ, où β représente le taux d’amortissement visqueux équivalent. Cette différence vient du fait que le type d’amortissement n’est pas le même dans les deux cas : d’une côté il y a l’amortissement visqueux β, d’autre part il y a l’amortissement hystérétique de la loi élastoplastique. Il s’ensuit de cette différence de définition qu’il n’est pas commode de faire un calage du modèle non-linéaire sur la base de la courbe β~γ. Il est toutefois important de vérifier a posteriori que les taux d’amortissement engendrés par le calage du modèle élastoplastique ne sont pas très différents par rapport aux valeurs de β qui correspondent aux courbes β-γ théoriques. En dehors de l’amortissement hystérétique, issu directement de la loi élastoplastique, il est également nécessaire de définir un amortissement « élastique », c’est-à-dire un taux d’amortissement de base, à appliquer dès le début de la sollicitation. La définition de cette composante d’amortissement (qui est calée à 1% - 3%) sert pour le bon conditionnement de l’équation d’équilibre dynamique et peut être introduite via un amortissement de type Rayleigh. Enfin, il est possible d’introduire une troisième composante d’amortissement, celle de l’amortissement numérique, qui résulte du choix d’un schéma d’intégration dissipatif. Cette troisième composante doit être utilisée avec précaution ; pour des applications courantes, elle est à éviter.
Liquéfaction - Un calage tout particulier des modèles de sol est exigé dans le contexte des études du risque de liquéfaction. Dans ce cas, il est nécessaire de faire appel à un modèle bi-phasique pour les zones potentiellement liquéfiables. Ceci permet de modéliser la montée de pression interstitielle qui survient dans ces matériaux peu perméables, lors d’une secousse sismique, phénomène qui peut conduire à l’état de liquéfaction. Le calage effectué dans ce cas consiste à montrer qu’un état liquéfié est bien obtenu sur une éprouvette de sol, consolidée à l’état de contrainte de la zone potentiellement liquéfiable, lorsqu’elle est sollicitée par le séisme théorique conduisant à la liquéfaction. Les paramètres les plus pertinents pour le calage vis-à-vis de la liquéfaction sont ceux qui gouvernent la réponse du sol en chargement selon l’axe hydrostatique (paramètres volumétriques), comme par exemple, l’angle de dilatance ou la règle de définition des déformations volumétriques plastiques etc.
5) Conditions aux limites : Frontières absorbantes - Modèles flottants
Dimensions de la zone à mailler - Un autre point subtil concernant la mise en œuvre d’une approche directe, concerne le « dimensionnement » du maillage et la définition des conditions aux limites. Tout d’abord, les dimensions du maillage doivent être suffisantes pour la description des phénomènes en jeu. Dans la direction verticale, le maillage est habituellement étendu jusqu’au niveau du substratum, où il peut être supposé que le comportement reste linéaire. Dans la direction horizontale, le maillage est étendu à une distance caractéristique égale à 4 à 5B, de part et d’autre de la structure, où B est la dimension caractéristique de la structure. Il s’ensuit que la dimension minimale d’un maillage pour la mise en œuvre d’une méthode directe d’IDSS est 10 fois la dimension caractéristique de l’ouvrage. Il est compris que ce critère, combiné avec les critères pour la taille des mailles, présentés plus haut, peut rendre prohibitif le coût d’un calcul d’IDSS par la méthode directe.
Conditions aux limites - Pour les problèmes où la sollicitation extérieure vient de la structure, la définition des conditions aux limites consiste à introduire des éléments de frontière absorbante le long du contour du maillage, dont le rôle est d’annihiler les réflexions parasites des ondes qui arrivent jusqu’aux extrémités du maillage. Les éléments de frontière absorbante couramment utilisés dans la pratique sont des amortisseurs visqueux standards qui ne sont exacts (en tant que frontières absorbantes) que pour une direction de propagation et une fréquence d’onde données. Pour passer outre ces limitations, plusieurs formulations de frontières absorbantes améliorées sont disponibles. Néanmoins, leur mise en œuvre reste relativement lourde et ces formulations restent peu utilisées dans les études courantes.
Pour les problèmes sismiques, le rôle des frontières absorbantes est à la fois la réduction des réflexions parasites et aussi l’introduction du mouvement sismique incident le long du contour du domaine modélisé en éléments finis. Pour atteindre ce deuxième objectif, il est souvent nécessaire de déterminer le mouvement au niveau du substratum (car en règle générale, les normes parasismiques fournissent le séisme de dimensionnement en surface du sol) : ce mouvement est utilisé comme le mouvement incident à la base du modèle. De plus, il faut déterminer le mouvement (en conditions de champ libre) sur une colonne de sol (du substratum jusque la surface), ce qui servira pour établir les conditions aux limites le long des parois latérales du modèle. Par ailleurs, la nécessité d’avoir un maillage suffisamment étendu dans la direction horizontale est expliquée par le fait que nous souhaitons établir le mouvement du champ libre à ses extrémités latérales. Pour les maillages dissymétriques, le calcul de la colonne du sol en champ libre doit être répété séparément pour la colonne du côté gauche et du côté droit du maillage.
Un contrôle qui doit toujours être fait, consiste à vérifier que le mouvement calculé en un nœud proche des frontières latérales du modèle est identique ou très proche du mouvement en champ libre. Cette vérification permet de s’assurer que le maillage est bien dimensionné pour le problème d’interaction étudié.
Phasage - Comme pour l’ensemble de problèmes géotechniques, il est aussi nécessaire pour les problèmes dynamiques, d’établir le vrai état de contrainte dans les géomatériaux avant de pouvoir introduire le chargement dynamique. Habituellement, toute étude d’IDSS est initiée par une phase de mise en gravité. A la fin de cette phase, les déplacements du système sont mis à zéro et les états de contrainte sont retenus dans la totalité du maillage. Suite à la complétion de la mise en gravité, il est possible d’introduire le chargement dynamique dans le système.
Modèles flottants - Toujours pour les problèmes sismiques, il est aussi important que la modélisation adoptée permette d’injecter simultanément la composante horizontale et la composante verticale du mouvement sismique. Pour la prise en compte de la composante verticale, on est souvent obligé à recourir à la méthode, dite « de modèle flottant » qui consiste à effectuer les étapes suivantes :
-
blocage des nœuds à la base du modèle et initiation sous poids-propre ;
-
détermination des réactions des nœuds bloqués sous poids propre ;
-
reprise des calculs sous poids propre en relâchant verticalement les nœuds à la base et en appliquant simultanément les forces gravitaires et les réactions calculées dans l’étape précédente : le modèle n’est retenu en aucun point selon la direction verticale (d’où le nom de « modèle flottant »), l’équilibre est assuré par l’égalité des réactions avec les charges gravitaires ;
-
enfin, suite à la mise en gravité, on introduit le séisme ; le fait d’avoir relâché les nœuds verticaux permet d’introduire aussi la composante verticale du mouvement sismique.
6) Choix d’un schéma d’intégration
La mise en œuvre de la méthode directe pour l’IDSS est complétée avec la définition du schéma d’intégration temporelle de l’équation d’équilibre dynamique. Les principes qui s’appliquent aux problèmes dynamiques non-linéaires généraux sont également applicables dans le cas des problèmes d’IDSS. Comme, il s’agit de problèmes non-linéaires, le schéma d’intégration temporelle et couplé avec une méthode d’intégration des lois de comportement non-linéaires, typiquement la méthode de Newton-Raphson ou la méthode de Newton-Raphson modifiée etc.
En règle générale, les problèmes de très courte durée (chocs, explosions etc.) sont traités par des schémas explicites. Ces schémas sont très efficaces si la matrice de masse peut être triangulée mais ils sont conditionnellement stables (les critères de stabilité conduisent souvent à des pas de temps très faibles). Pour les problèmes sismiques, on fait appel à des schémas implicites, le plus couramment utilisé étant le schéma d’intégration de Newmark (qui est inconditionnellement stable en régime linéaire pour un jeu donné des paramètres d’intégration).
Le choix d’un schéma dissipatif (entraînant de l’amortissement numérique) peut également être proposé de manière à faciliter la convergence de la solution pour des problèmes fortement non-linéaires.
Dans tous les cas, le choix d’un schéma d’intégration, approprié à un problème donné, avec la définition de tous les paramètres associés (tolérances, nombre d’itérations, stratégie pour gérer la divergence etc.) nécessite une très bonne connaissance des notions théoriques et aussi une expérience importante quant à la typologie des problèmes traités (sismiques, chocs, dynamique rapide, problèmes vibratoires etc.). Comme principes généraux, il est conseillé de commencer les analyses avec des schémas non-dissipatifs et avec des tolérances relativement strictes (de l’ordre de 10-4). A la fin de chaque analyse, il faut examiner avec prudence le fichier des résultats détaillés afin de vérifier que les résidus de chaque incrément ne dépassent pas les tolérances et que la convergence est obtenue sur la totalité des mailles du modèle.
PARTIE 2 - ÉLÉMENTS PRATIQUES
$translationBooksChapitre A. Comprendre les éléments finis
Chapitre A. Comprendre les éléments finis
A.1 Que fait le logiciel dans un calcul aux éléments finis ? Exemple des structures à poutres.
A.2 Concrètement qu'est-ce qu'un élément fini ?
Annexe 1 - Fichier de l'exemple de calcul matriciel
$translationBooksA.1 Que fait le logiciel dans un calcul aux éléments finis? Exemple des structures à poutres.
A.1 Que fait le logiciel dans un calcul aux éléments finis? Exemple des structures à poutres.
Cette introduction a pour finalité de montrer, sur un exemple simple, ce qui se cache derrière un calcul statique conduit avec un logiciel EF à barres.
Dans le wiki, par abus de langage, le terme “barre” est souvent employé pour désigner des éléments de type “poutre” et non pas exclusivement des éléments de type “barre” au sens strict (i.e. travaillant uniquement en effort normal).
Quelques rappels :
Le calcul informatique est basé sur une représentation de la structure par un ensemble de barres dont les intersections sont des nœuds. Son but est de déterminer les déplacements des nœuds de la structure, c’est-à-dire les déplacements des abouts des barres, sous les charges appliquées.
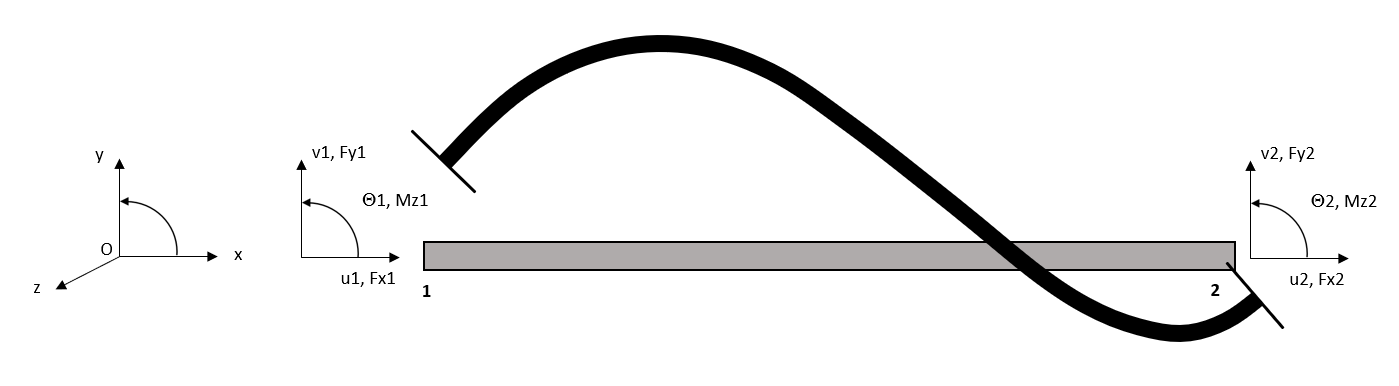 Figure 1 – Convention de signes – efforts et déplacements
Figure 1 – Convention de signes – efforts et déplacements
Les forces aux extrémités de la barre dépendent linéairement des déplacements en ces points. On montre qu’il existe une relation matricielle efforts-déplacements pour une barre reliant deux nœuds i et j, telle que, pour un repère donné, [Kij][qij]=[Fij] (figures 1 et 2), permettant d’exprimer les composantes des vecteurs [Fij] en fonction de celles des vecteurs [qij]. [Kij] est appelée la matrice de raideur de la barre, [Fij] le vecteur des efforts aux nœuds et [qij] le vecteur des déplacements des nœuds.
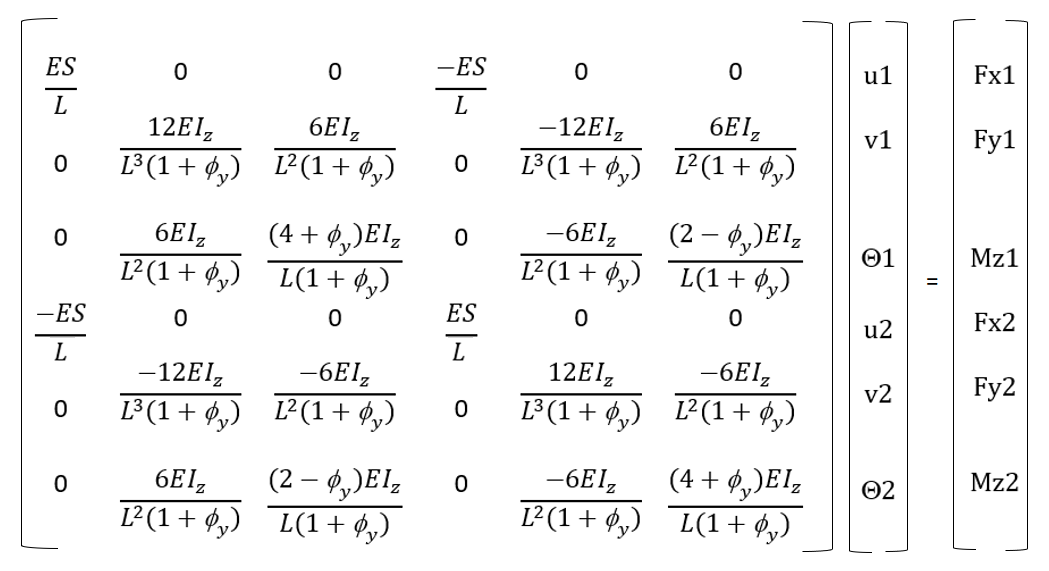 Figure 2 - Matrice de raideur d'une poutre bi-encastrée
Figure 2 - Matrice de raideur d'une poutre bi-encastrée
La matrice [Kij*], associée au repère général, se déduit de la matrice [Kij] exprimée dans le repère local de la barre en lui appliquant une transformée [Λ]T[Kij][Λ] (figure 3), permettant de rendre les déplacements compatibles avec ceux du repère général. [Kij*]=[Λ]T[Kij][Λ] est alors la matrice de raideur de la barre dans le repère général.
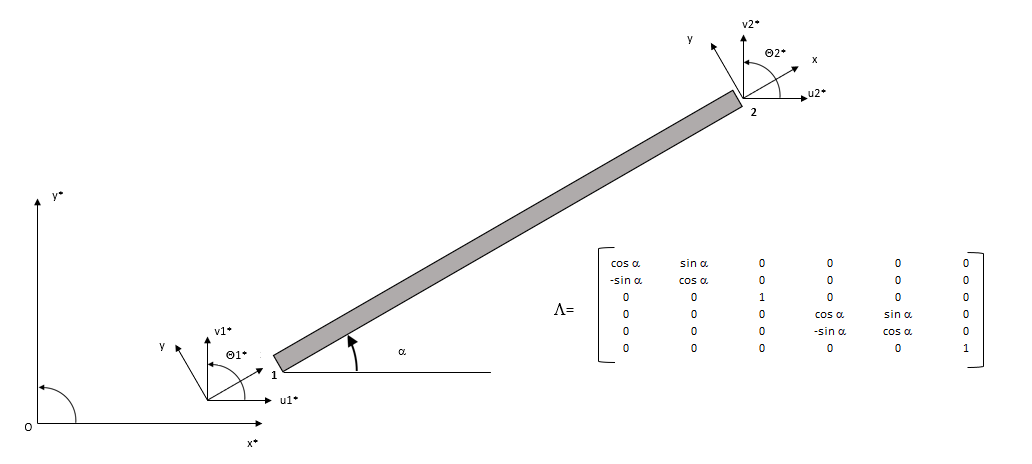 Figure 3 - Rotation des matrices
Figure 3 - Rotation des matrices
Pour calculer les déplacements de tous les nœuds, le logiciel :
-
« assemble » les matrices [Kij*] de chacune des barres pour former la matrice de raideur globale [K] de la structure (figure 4),
-
inverse [K] → [K]-1,
-
multiplie la matrice [K]-1 par celle [F] des efforts extérieurs, préalablement ramenés aux nœuds (s’ils sont appliqués sur une barre ailleurs qu’aux extrémités), dans le repère global, pour calculer le vecteur des déplacements [q].
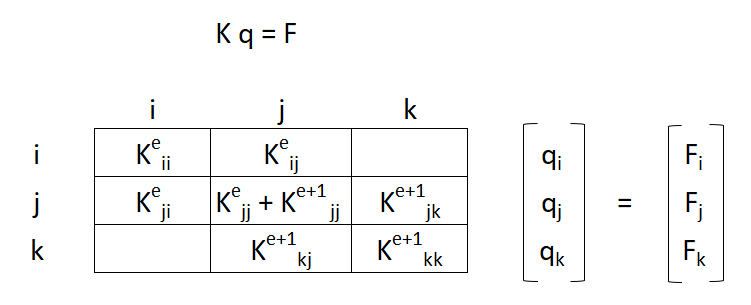 Figure 4 - Principe de l'assemblage
Figure 4 - Principe de l'assemblage
Enfin, pour calculer les efforts internes de la structure, le logiciel multiplie la matrice de raideur [Kij] de chaque barre par le vecteur des déplacements [qij], dans le repère local, aux nœuds i et j. Il obtient ainsi les efforts aux nœuds et les additionne, le cas échéant, aux réactions de la barre bi-encastrée (i.e. les efforts introduits dans le modèle global, mais ici projetés dans le repère local de la barre) - voir le second exemple ci-dessous. Les efforts et déplacements le long des barres se déduisent aisément de ceux des nœuds à l'aide des formules de la RDM.
Application à un exemple simple :
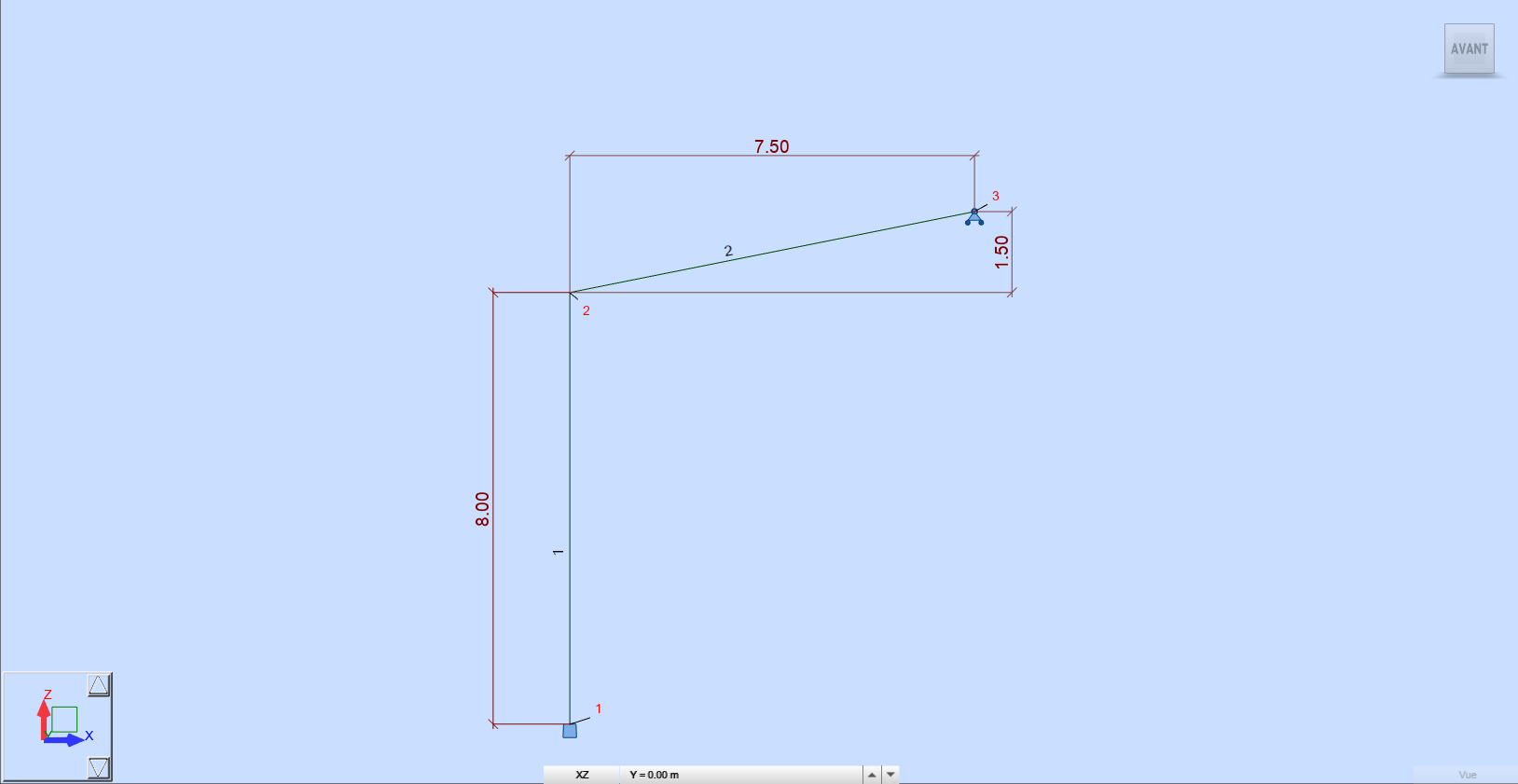
Figure 5 - Structure calculée
Cet exemple est traité à l’aide d’un tableur dont le fichier source est fourni dans la partie 3 du guide - il est téléchargeable en cliquant sur le lien ci-après. Fichier source au format Excel de l'exemple ci-dessous.
Ce tableur couvre deux exemples : l’exemple développé ci-après pour une structure à 2 barres (pour rester facilement lisible en format papier) et un second exemple avec 4 barres. Ces exemples permettent de visualiser et de comprendre l’enchaînement des tâches.
Les caractéristiques de barres nécessaires pour un problème plan sont : la section S, l’inertie I, le module d’Young E, la longueur L et l’orientation α, par exemple par rapport à l’horizontale.
| Barre | 1 | Barre | 2 |
| Section = | 1.000 m² | Section = | 1.500 m² |
| Inertie = | 0.083 m4 | Inertie = | 0.281 m4 |
| α = | 1.571 rad | α = | 0.197 rad |
| L = | 8.000 m | L = | 7.649 m |
E = 36 000 MPa pour toutes les barres.
On détermine aisément pour chaque barre les valeurs numériques de la matrice de raideur à partir des valeurs littérales de la figure 2.

Barre 1 : matrice de raideur

Barre 2 : matrice de raideur
On applique à ces deux matrices, la transformée permettant de les rendre compatibles avec le repère général.
Matrice de rotation pour α = 1.571 Rad :
Et sa transposée :
Matrice de rotation pour α = 0.197 Rad :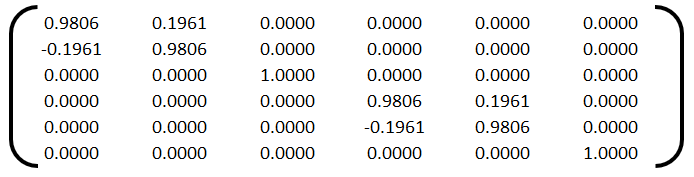
Et sa transposée :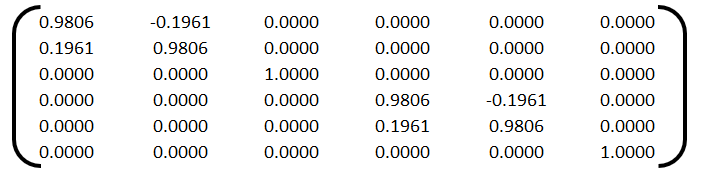
Barre 1 - Résultat de l’opération [K*]=[Λ]T[K][Λ] :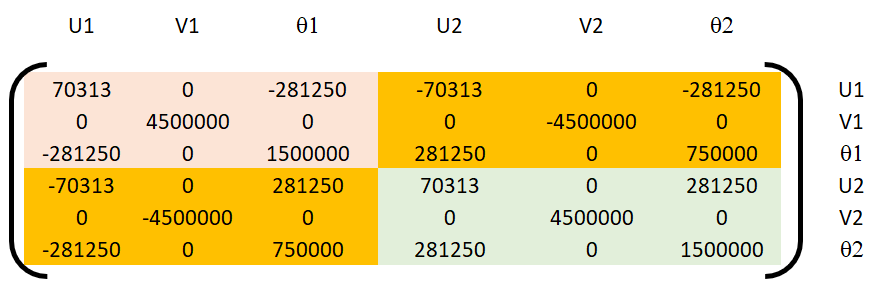 Barre 2 - Résultat de l’opération [K*]=[Λ]T[K][Λ] :
Barre 2 - Résultat de l’opération [K*]=[Λ]T[K][Λ] :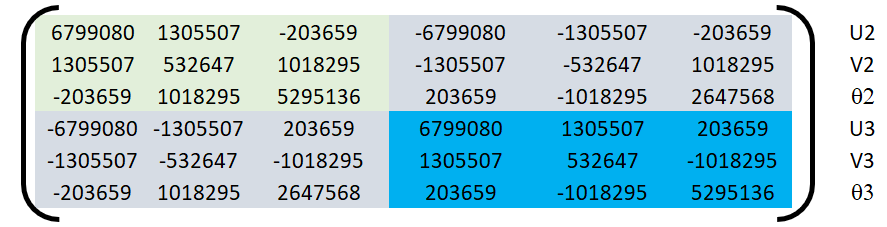
Toutes ces matrices unitaires sont ensuite assemblées, c’est-à-dire que l’ensemble des valeurs matricielles relatives à un même déplacement nodal sont cumulées.
Pour notre exemple, cela revient à sommer les valeurs des deux matrices correspondant aux nœuds communs (dans le cas général, les barres ne relient pas toujours deux nœuds dont la numération se suit comme ici) :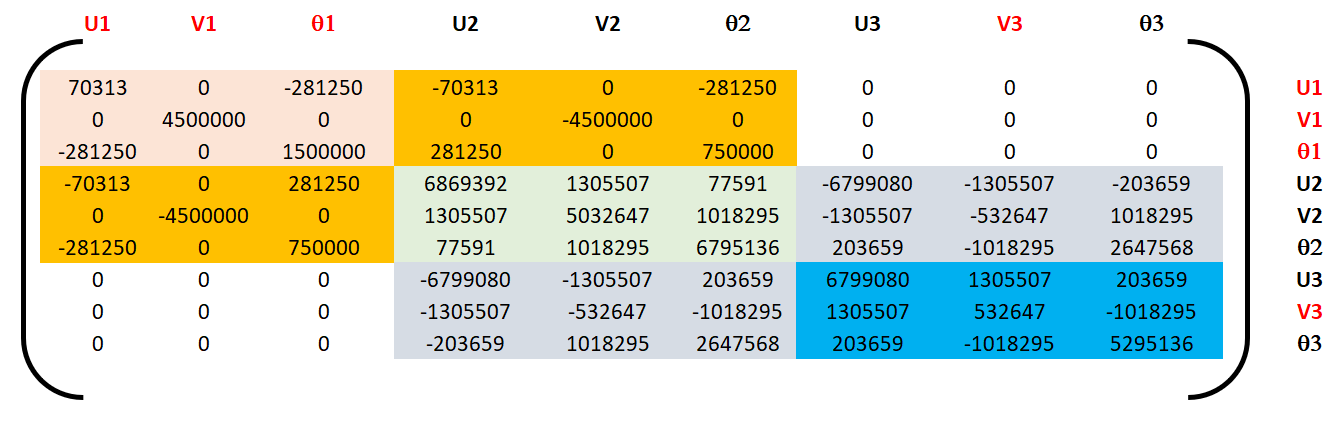
Les composantes des déplacements bloqués peuvent être supprimées de la matrice puisque nous connaissons déjà leur valeur, elle est nulle: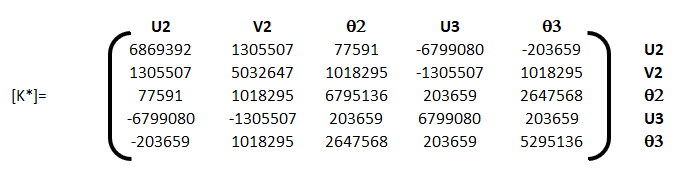
Cette matrice s’inverse facilement avec le tableur :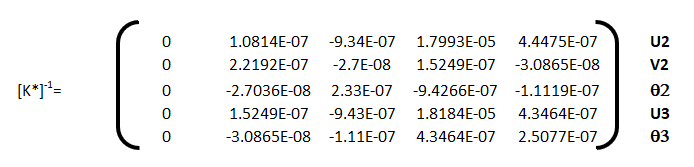
Chargement 1 : Forces extérieures appliquées sur un nœud
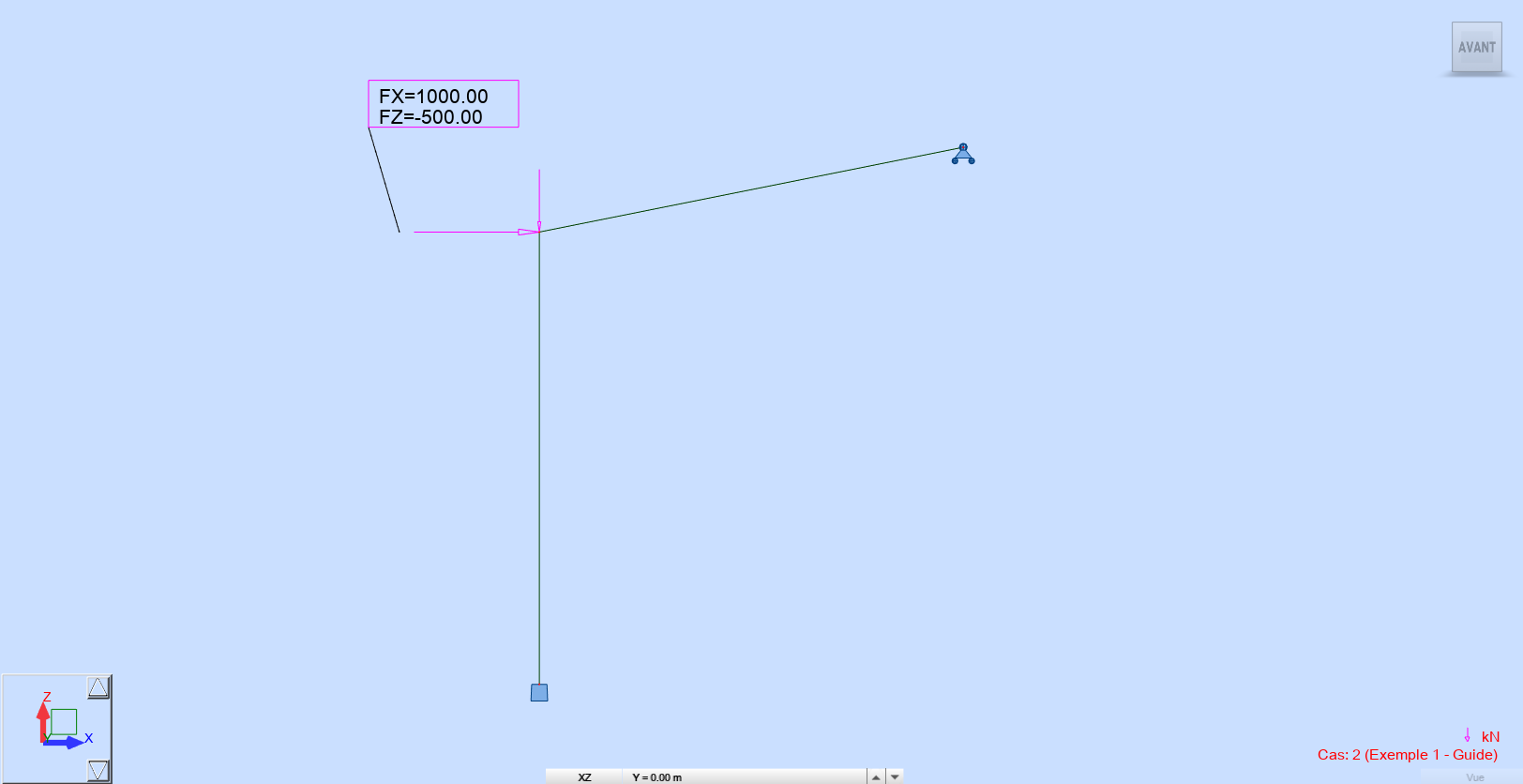
Figure 6 - Définition du chargement
On calcule les déplacements des noeuds (dans le repère général):
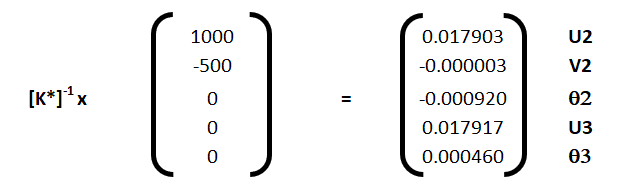
On peut déterminer les efforts dans le poteau (barre 1) après transformation préalable des déplacements dans le repère local de la barre :
On a une compression de 12,68 kN, un tranchant de 1000 kN et un moment qui change de signe sur la barre (on vérifie bien que 1000 kN * 8 m - 3654,89 = 4345,11 kN.m en pied - ok).
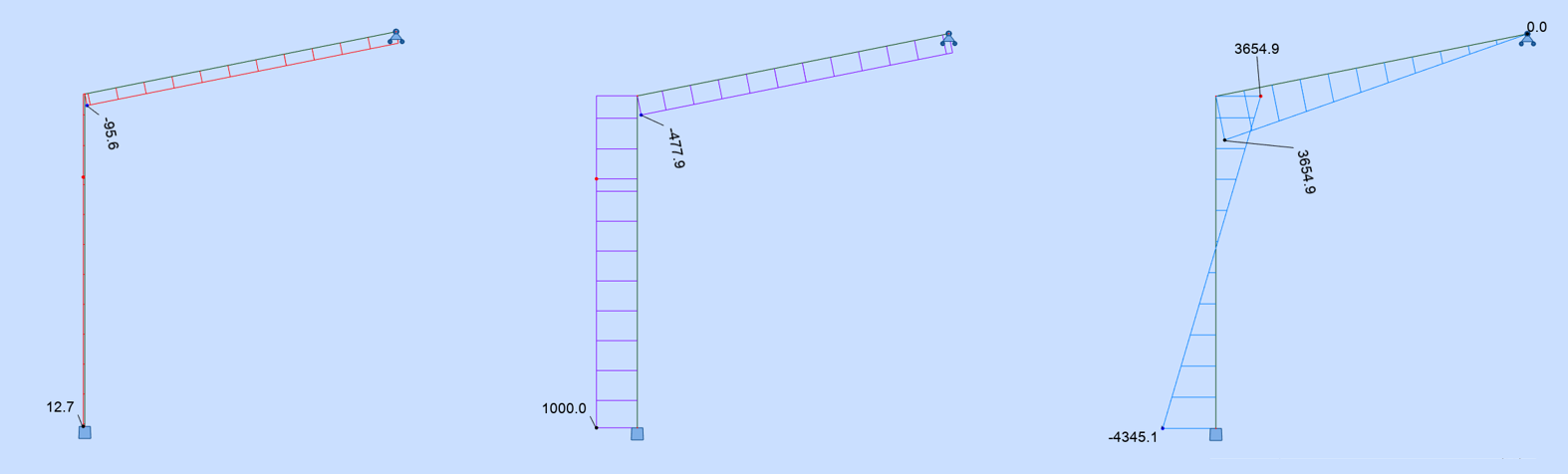
Figure 7 - Diagrammes N, V, M – exemple 1
Chargement 2 : Forces extérieures appliquées sur une barre (i.e. ailleurs qu’aux nœuds).
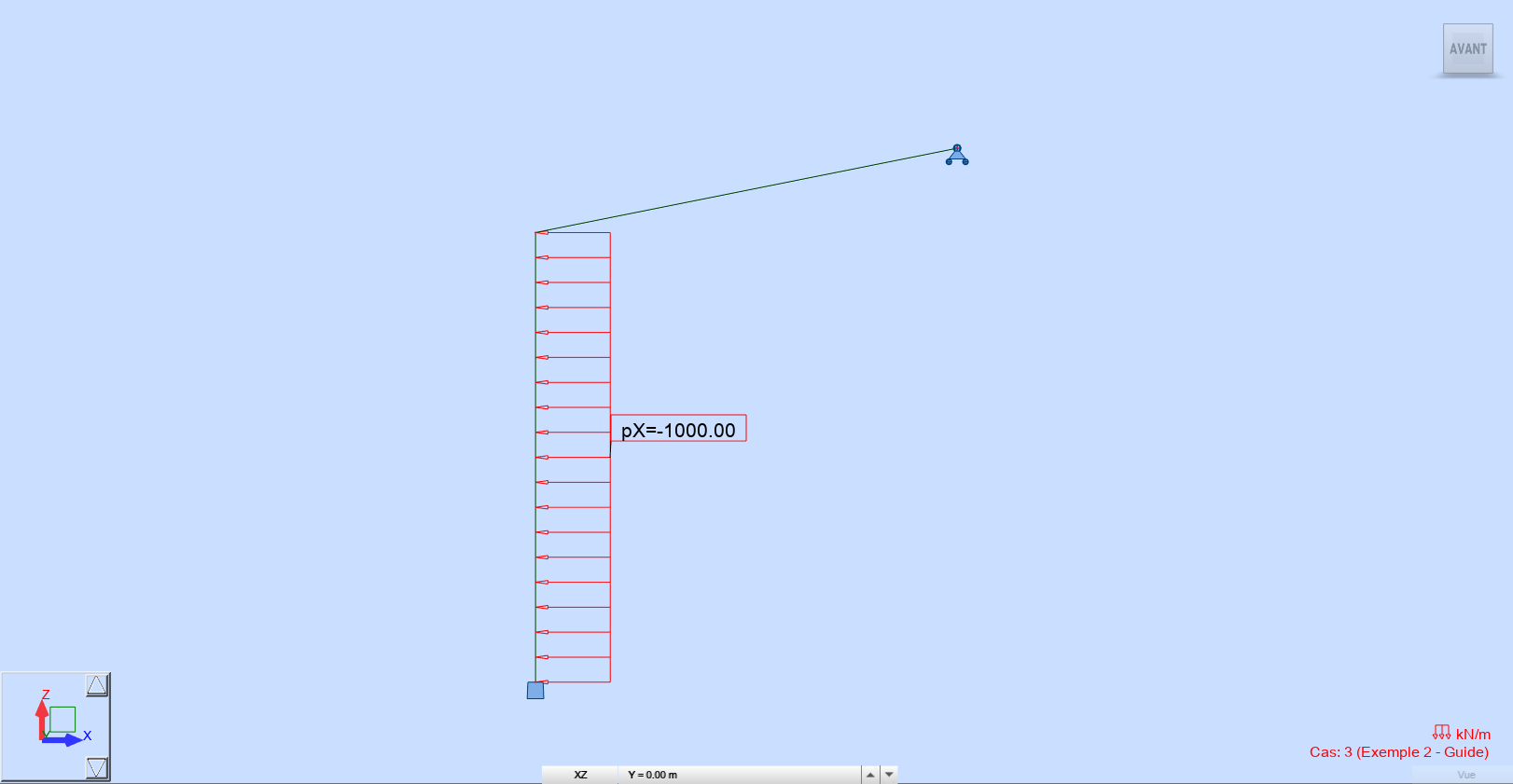
Figure 8 - Définition du chargement
Dans ce cas, il faut préalablement calculer les réactions d’appui de la barre bi-encastrée sous ces efforts, car ce sont elles qui doivent être injectées dans la matrice des charges extérieures (le logiciel ne connaît que les nœuds !). Un formulaire de poutre bi-encastrée suffit. Il faut veiller, bien entendu, au respect des conventions de signes.
Application à la charge répartie horizontale p=-1000 kN/m sur le poteau (figure 8). On sait dans ce cas que les moments d’encastrement valent -pL²/12 et les tranchants aux appuis +/-pL/2; donc, avec L=8 m et en tenant compte de la convention de signes:
En multipliant [K*]-1 par ces efforts, on obtient les valeurs des déplacements de tous les ddl. Il suffit ensuite de multiplier la matrice de raideur de la barre 1 par ces déplacements pour récupérer les efforts aux nœuds.
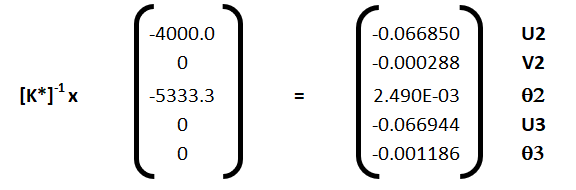
On peut calculer les efforts dans le poteau (barre 1) après conversion préalable des déplacements globaux dans le repère local de la barre…

… et les additionner avec les efforts d’encastrement parfait, avec la convention de signes adéquate: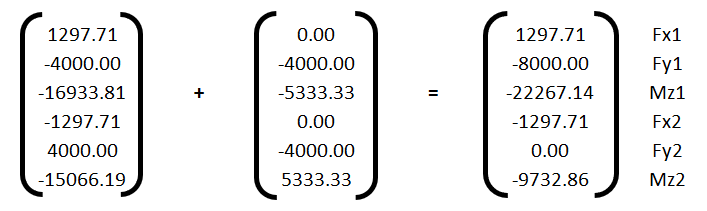
On a une de compression de 1298 kN , un tranchant qui passe de 0 à 8000 kN (pL=1000 kN/m * 8 m = 8000 kN) et un moment en pied très fortement majoré par rapport au moment d’encastrement parfait.
La même méthodologie s’applique à la barre 2 pour obtenir les efforts aux nœuds.
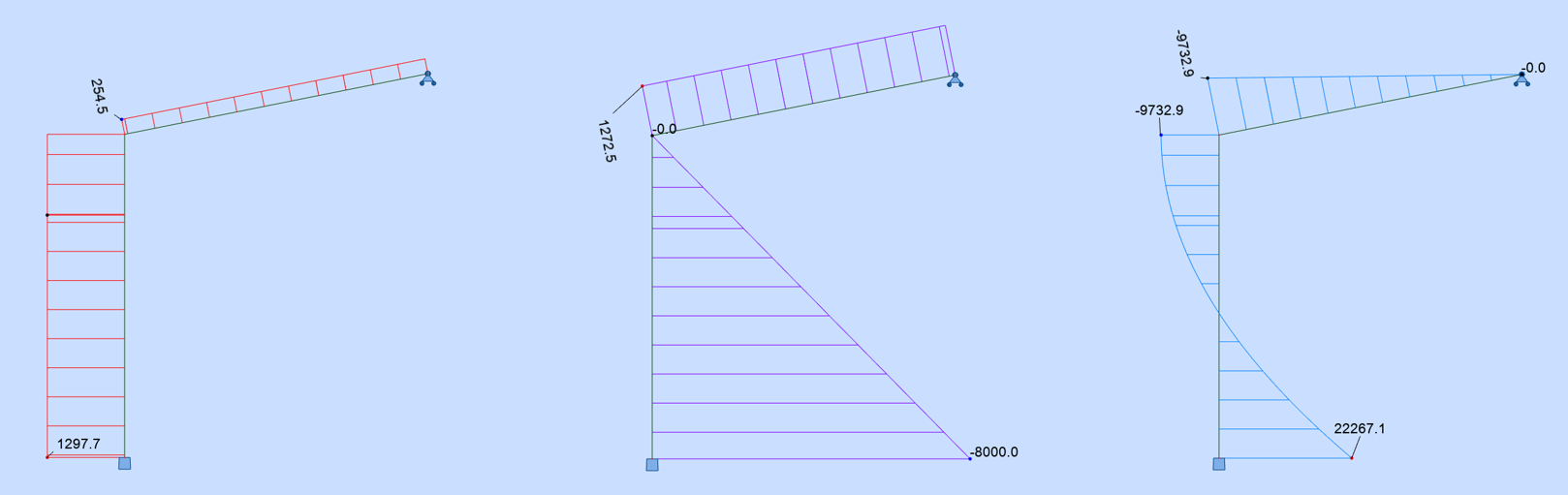
Figure 9 - Diagrammes N, V, M – exemple 2
Cas où les barres présentent des différences de raideur notable :
A titre d’exemple, on rigidifie très fortement la barre verticale. On décide, en gardant une longueur de 8 m, de passer sa section droite à 1 m * 1012 m (b*ht). On montre ci-après la matrice [K*] ; on ne peut que constater l’écart entre la valeur plus grande et la plus petite … ce qui peut aboutir dans certains cas à des instabilités numériques (la résolution conduit à diviser les termes de la matrice les uns par les autres).

Figure 10 - Matrice avec valeurs disparates
$translationBooksA.2 Qu’est-ce qu’un élément fini ?
A.2 Qu’est-ce qu’un élément fini ?
La détermination des efforts dans les éléments est réalisée à la suite du calcul des déplacements des nœuds. La méthode est spécifique pour chaque type d’éléments et dépend du logiciel utilisé.
Le principe est néanmoins commun à tous les logiciels, il consiste à « isoler » un élément pour calculer les efforts aux points de Gauss à partir des déplacements des nœuds.
La position des points de Gauss est normalement précisée dans la documentation du logiciel; dans le cas d’un élément de coque à 4 nœuds comme ci-dessous, ils pourraient être situés à une distance du bord de l’élément égale à 1/5 de sa largeur environ.

Exemple d’un élément à 4 nœuds
Les efforts au centre de l’élément sont calculés comme la moyenne des efforts aux points de Gauss, les efforts aux nœuds sont extrapolés à partir des points de Gauss.

Pour résumer, le logiciel calcule :
-
les efforts aux points de Gauss G1 à G4 à partir des déplacements des nœuds n1 à n4 ;
-
les efforts au centre C qui sont la moyenne des efforts aux points de Gauss G1 à G4 ;
-
les efforts aux nœuds n1 à n4 qui sont extrapolés à partir des efforts en G1 à G4.

Ces calculs étant réalisés pour tous les éléments, au final il y a autant d’efforts aux nœuds qu’il y a d’éléments connectés sur ce nœud (ici 4 éléments E1 à E4 pour le nœud n1).
Il peut alors en déduire :
-
soit l’effort maximal sur le nœud (maximum des efforts calculés à partir des éléments E1 à E4) ;
-
soit l’effort moyen (moyenne des efforts calculés à partir de E1 à E4).
Principales remarques dans les utilisations courantes.
-
En règle générale, les éléments quadrangulaires conduiront à une meilleure précision des résultats que des éléments triangulaires.
-
Ce sont les résultats aux points de Gauss qui sont le plus précis, mais ils ne sont généralement pas accessibles aux utilisateurs.
-
Les résultats aux centres des éléments sont plus fiables que les efforts aux nœuds, car ils ne sont pas extrapolés.
-
C’est à l’ingénieur de choisir en fonction du comportement de la structure le type de résultat (maximal, moyen, lissé, etc..) ; il n’y a pas de règle prédéfinie.
Exemple d'une charge sur une dalle de pont illustrant les écarts de résultats lors d'un calcul EF.
$translationBooksChapitre B. Objectifs de calcul et caractéristiques nécessaires de l’outil
Chapitre B. Objectifs de calcul et caractéristiques nécessaires de l’outil
La réalisation d’un modèle de calcul par éléments finis comprend plusieurs étapes. Le choix de l’outil est prépondérant et dépend de plusieurs critères. Une modélisation réussie demande une bonne organisation initiale.
B.1 à B.6 Critères à prendre en compte
$translationBooksB. Objectifs du calcul et caractéristiques nécessaires de l’outil
B. Objectifs du calcul et caractéristiques nécessaires de l’outil
La réalisation d’un modèle de calcul par éléments finis comprend plusieurs étapes. Le choix de l’outil est primordial et dépend de plusieurs critères.
B.1 En fonction de l’objet à modéliser
Tout d’abord, le logiciel de calcul doit être adapté à l’objet à modéliser.
a) Entre un pont (ouvrage courant à faible portée ou ouvrage complexe à plusieurs travées), un bâtiment ou un ouvrage géotechnique (soutènement, tunnel, barrages…), les problématiques sont différentes.
En fonction de la taille de l’objet, on peut définir une ou plusieurs échelles de modélisation, notamment:
-
une échelle géologique (qui vise à traiter une structure dans son environnement en fonction des données géologiques) ;
-
une échelle globale qui vise à traiter une structure dans son ensemble (calculs longitudinaux de flexion générale pour les ponts par exemple) ;
-
une échelle semi-locale avec un maillage plus serré pour certains éléments de la structure (calculs transversaux sous les actions des essieux pour les ponts, par exemple) ;
-
une échelle locale, avec une modélisation très raffinée et un post traitement des résultats (calculs de béton armé pour le poinçonnement ou des aciers de diffusion ou de frettage…).
b) Un objet peut donner lieu à plusieurs modélisations qui se complètent entre elles.
| Echelle | GLOBALE | SEMI-LOCALE | LOCALE |
| Ouvrage d’Art | Flexion longitudinale | Flexion transversale | Concentrations de contraintes (zone d’ancrage ou de déviations des câbles, appui concentré) |
| Bâtiment | Descente de charge / Contreventement (vent, séisme) / Calcul dynamique | Flexion locale des éléments horizontaux (planchers, radiers) | Charges concentrées, accidentelles (zone d’ancrage, supports de machines) |
| Géotechnique | Remblais, soutènement | Arrachement tirant dans massif de sol, écoulement,… |
c) Dans le cas d’une structure dont la cinématique de construction a un impact sur l’état final, le logiciel doit pouvoir autoriser la simulation complète du phasage, en permettant entre autres une activation sélective des éléments (comme la mise en tension des câbles de précontrainte et des haubans par exemple), ce qui permet de travailler sur la partie de structure en cours de construction.
d) Si un calcul dynamique est nécessaire (par exemple un calcul sismique avec prise en compte des effets du sol ou un calcul vibratoire ou encore un problème de dynamique rapide comme une explosion), il ne peut pas être traité avec tous les logiciels.
e) Les calculs non-linéaires ne sont pas systématiquement possibles (calcul avec non-linéarités matérielles, appuis élasto-plastiques, calcul des grands déplacements au second ordre pour la vérification au flambement, etc.)
f) Les modélisations de structure à câbles (dont la rigidité transversale à la flexion et à la torsion est peu importante par rapport à la rigidité longitudinale ) sont aussi particulières et assurées seulement par certains logiciels.
g) La détermination d’un champ thermique (chargement volumique déterminé à partir d’une variation de la température et du coefficient de dilatation thermique du matériau) peut nécessiter l’utilisation d’un module complémentaire au logiciel.
h) La modélisation des fondations, comme le cas d’un radier présentant un soulèvement, est généralement liée à des calculs non-linéaires et rejoint donc le point d).
B.2 En fonction de la phase d’étude
La phase d’étude d’un ouvrage a un impact sur le niveau de précision attendu des calculs.
-
En phase d’Etudes Préliminaires, la modélisation doit rester pragmatique, ne jamais être complexe et donner des résultats majorés.
-
En phase d’Avant-projet ou de Projet, il s’agit d’établir un prédimensionnement de l’ouvrage qui sert de base à la préparation d’un appel d’offres. Les calculs sont plus accomplis, voire complexes, mais rarement exhaustifs. Les modèles doivent être rapides, conserver une certaine souplesse et faciles à corriger, de telle sorte qu’ils ne brident pas le projet et permette de facilement tester des variantes.
-
En phase d'Exécution, le projet étant arrêté, les calculs doivent être complets, peuvent être complexes, doivent donner des résultats concrètement exploitables et doivent garantir un dimensionnement à la fois sûr et optimisé.
A titre indicatif, le tableau ci-dessous présente le niveau de détail généralement attendu par phase. Selon les spécificités du projet et les souhaits du client, le contenu des phases peut néanmoins être amené à varier :
| Objet \ Avancement | Etude préliminaire | AVP | PRO | EXE |
| Ouvrage d’Art, Bâtiment industriel, Ouvrage de GC | Ratios, Retour d'expérience, Modèle global simplifié (modèle 2D de préférence) | Modèle global | Modèle global + vérifications semi-locales, voire locales pour points critiques | Modèle global + semi-local + local généralisé |
B.3 En fonction des objectifs de vérification
Pour un même objet et une même phase d’étude, on peut être amené à monter plusieurs modèles qui traiteront chacun de vérifications différentes.
Dans la mesure du possible, on cherche à ce qu’un même modèle réponde à un maximum de vérifications mais on doit souvent découpler les problématiques.
B.4 En fonction des résultats attendus
Les résultats exploitables par les différents logiciels peuvent influencer les choix.
a) Des modules intégrés de post-traitement rendent certains logiciels intéressants, notamment ceux qui permettent d’obtenir un ferraillage des sections de béton armé à partir des sollicitations, ou ceux qui incorporent la vérification de profilés métalliques au flambement/déversement ou la vérification d’assemblages classiques. Il est indispensable au préalable de vérifier la conformité du post-traitement avec les règlements de référence du projet.
b) Les types de résultats en sortie peuvent aussi être variés et plus ou moins adaptés (listings, diagrammes des efforts, cartographies, enveloppes des combinaisons avec ou sans conservation des concomitances).
B.5 En fonction des délais et des ressources
En termes de délais, et donc de budget, il faut bien distinguer le temps de modélisation (géométrie, chargements, combinaisons, …), le temps de calcul, le temps de mise au point/réglage (débogage des erreurs, vérifications des conditions aux appuis, …) et enfin le temps d’analyse. Ces durées peuvent varier de manière significative suivant les logiciels, car leur interface utilisateur est plus moins intuitive (interface de conception qui peut être soit graphique, soit programmable dans une fenêtre de commande ou par l’intermédiaire de tableurs). L’extraction des résultats n’est pas nécessairement immédiate, il peut être utile de repérer les points critiques.
Les ressources disponibles au sein du bureau d’études guident également le choix du type de calcul : le matériel informatique, sur lequel le logiciel est installé, doit être libre, tout comme la licence d’utilisation qui peut être accaparée par un autre utilisateur. Le planning de disponibilité des outils peut jouer sur les délais et, éventuellement, conduire à changer de logiciel.
Si le bureau d’étude possède un type de matériel à capacité réduite, le degré de complexité des calculs est diminuée d’autant. Et si le modèle de calcul compliqué est maintenu, le bureau d’étude ne doit pas « bricoler » un modèle adapté à la capacité de ses matériels, car les simplifications adoptées peuvent alors entraîner des problèmes de justesse des résultats. Le bureau d’étude a alors tout intérêt à sous-traiter le calcul.
Pour des ouvrages importants, il peut être préférable de mettre en œuvre deux niveaux de modélisation, en utilisant des sous-modèles, car un modèle unique peut vite devenir démesuré en taille, et être, de ce fait, difficile à structurer et à manipuler. Il faut cependant être capable de relier les modèles entre eux. Par ailleurs, le besoin de capacités de calcul spécifiques peut également conduire à la scission de modèles et à l'emploi de logiciels différents.
Une autre raison de scinder les modèles comme décrit ci-avant, peut être liée au calendrier des études (conséquence de l’organisation des projets) : le calcul de la totalité de l’ouvrage précède parfois de plusieurs mois, pour les projets importants, le calcul de certaines parties de l’ouvrage. Rien n’empêche, par post traitement, de pallier certaines lacunes du logiciel, en extrayant les résultats d’un sous-modèle et de les traiter manuellement ou par l’intermédiaire d’un autre logiciel.
Une ressource également importante est le personnel, c’est-à-dire l’ingénieur chargé de la modélisation. Celui-ci doit être formé à l’utilisation du logiciel. Dans le cas où ce dernier est novice en la matière, le temps d’apprentissage ne doit pas être sous-estimé, la durée de conception et de mise au point du modèle pouvant être amplifiée grandement. La mise en place d’un tutorat avec un ingénieur senior est fortement recommandée, malgré l'investissement en temps que cela représente.
B.6 En fonction du confort d’utilisation
Enfin, le confort dans l’utilisation du logiciel est primordial.
a) Un logiciel avec une notice complète (d’installation, de prise en main et d’exploitation) est toujours plus appréciable. La présence d’un catalogue d’exemples d’applications, de tutoriaux et de manipulations est un plus.
b) La possibilité de programmation (création puis lecture d’un code en texte dans un langage de programmation propre) permettant une entrée des données intuitive et rapide est un atout. Elle peut offrir de nombreuses possibilités à l’utilisateur, par exemple, automatiser la modélisation de structures-types simples et répétitives ou encore ajuster la mise en page des résultats, en fournissant des sorties textes ou Excel adaptées à la sous-structure étudiée.
c) La confiance dans le logiciel assure un gain de temps non négligeable, en évitant certaines vérifications superflues. Pour cela, la présence de mises à jour régulières est un indicateur, tout comme l’existence d’une hotline technique disponible et réactive, capable de fournir une assistance ponctuelle sur une modélisation spécifique. La confiance ne dispense bien sûr pas des vérifications de modèle explicitées dans ce guide.
d) La version du logiciel peut également jouer dans le choix, dans le cas où certaines fonctionnalités ont été ajoutées/enlevées ou lorsque la stabilité et/ou la rapidité d’une version n’est pas satisfaisante.
e) Certains logiciels possèdent des bibliothèques complètes (matériaux, profilés, boulons, assemblages…) qui génèrent un gain de temps. Des fonctionnalités spécifiques aux ouvrages de génie civil sont aussi possibles, comme l’application de chargements automatiques réglementaires (types A(l), Bc, LM1, LM2…).
f) Selon le règlement qui s’applique au projet, le logiciel peut proposer des charges, des combinaisons et des vérifications pré-programmées. C’est un élément de confort, mais qui doit toujours être vérifié sur des cas simples.
g) Un affichage de la structure en pseudo-volumique est un avantage, car cela permet de vérifier visuellement le type et l’orientation des profilés ou barres. En outre certains logiciels permettent un export 3D qui constitue un support de communication très utile en réunion avec les parties prenantes (voir en complément le chapitre E.3 pour la partie BIM).
h) Un logiciel qui spécifie la ligne du fichier de données présentant une erreur ou la liste des objets mal modélisés (superpositions, …) dans le modèle spatial offre un réel avantage. Les messages d’erreur doivent être clairs et précis (si possible dans la langue de travail de l’ingénieur).
Retour d'expérience:
Le REX (Retour d’expérience) est important : les réunions ou fiches REX doivent permettre de tirer les enseignements positifs et négatifs de projets en cours ou terminés. Elles portent sur les méthodes employées, mais aussi les moyens informatiques utilisés ou encore la production réalisée.
$translationBooksB.7 Organisation du calcul
B.7 Organisation du calcul
C’est une étape indispensable à réaliser au démarrage de l’étude.
a) Réflexion préliminaire sur la modélisation
Une étape primordiale s’impose au modélisateur : celle de l’analyse du fonctionnement d’ensemble de la structure. Il serait effectivement insensé de démarrer la modélisation d’un ouvrage avant même d’en comprendre le comportement global. Un premier croquis manuel de la structure révèle dans un premier temps la bonne compréhension du fonctionnement et servira de trame à la construction du modèle.
Cette analyse de fonctionnement permet avant tout de distinguer les éléments principaux traduisant le comportement global de l’ouvrage. Parmi ces éléments principaux, on distinguera par exemple :
-
pour les ouvrages d’art : la structure porteuse du tablier, la structure des appuis, les contreventements ;
-
pour les bâtiments en béton armé et en béton précontraint : les poteaux, voiles et dalles ;
-
pour les charpentes de bâtiments : les poteaux, les poutres, les éléments de contreventement.
La modélisation s’appuie nécessairement sur des données d’entrée, a minima :
-
une note d’hypothèses générales, qui contient une description de l’objet, les règlements appliqués et les charges appliquées ;
-
des croquis ou des plans généraux de l’objet à modéliser ;
-
un principe général de construction ;
-
une ébauche de fonctionnement statique et éventuellement dynamique.
La modélisation ne se substitue pas à ces éléments de réflexion préliminaire.
BIM et modélisation : Le modélisateur peut être tenté d’employer les données d’entrée de façon automatisée pour construire son modèle. C’est un argument fréquent des éditeurs de logiciels. Dans ce cas, il devra être particulièrement vigilant à la qualité des entrants fournis (il n’est en effet pas rare de trouver des modèles 3D avec des non-sens géométriques) et au niveau de détail des données d’entrée (quantité de trémies par exemple). Dans le cas d’un traitement automatisé, il faudra être attentif à la procédure de construction de la géométrie, notamment au niveau des connexions. L’étape d’analyse du fonctionnement d’ensemble précédemment évoquée est ainsi le moyen de prévenir toute anomalie.
b) Validation des données d’entrée / Synthèse des entrants
Tous les documents définissant les hypothèses de la géométrie, des matériaux, des chargements doivent être référencés avec leur provenance, leur indice et la date d’émission.
Il convient de valider la cohérence de ces différents documents. Par exemple, les plans architecturaux et les plans du gros œuvre sont-ils cohérents entre eux ? Y a-t-il des décalages géométriques entre les différents fichiers de plans ? Les données sont-elles exhaustives ? Observe-t-on d’ores et déjà des infaisabilités (descente de charge au cheminement complexe, absence de contreventement…) ?
Ce travail de synthèse permet de mettre en évidence les données d’entrées manquantes et/ou susceptibles d’être modifiées et de définir les mesures conservatoires prises en compte pour pallier les données manquantes.
En fonction de cette analyse préliminaire, certaines décisions s’imposeront immédiatement au modélisateur : échanges avec le donneur d’ordre, révision de la géométrie de l’ouvrage (révision de la conception), entrée de données paramétrables…
Cette phase de synthèse prendra idéalement la forme d’une « Note de Modélisation » qui évoluera au cours de l’avancement du modèle. L’objet est de faire valider par tous les participants de l’étude les hypothèses très rapidement, afin d’éviter les modifications qui sont souvent longues et complexes.
c) Spécificités de l’étude
Toutes les spécificités de l’étude doivent être listées au démarrage :
-
les contraintes physiques du projet (soutènements importants, zone urbaine, phasage de construction, …) ;
-
les contraintes de l’étude (planning serré, nombreuses interfaces, données manquantes, …) ;
-
les particularités de la modélisation (taille du modèle, non linéaire, séisme, …) ;
-
les exigences et les points sensibles du projet (structure très élancée, très dissymétrique, vents importants, etc.).
Il est nécessaire de montrer que la modélisation va prendre en compte tous ces points.
d) Planning de l’étude
Il doit faire apparaître clairement :
-
les dates des principales étapes de la modélisation (géométrie, matériaux, chargements, interface ou interaction sol-structure, combinaisons, etc..) ;
-
les dates jalons pour la réception des données d’entrées manquantes ou susceptibles d’être modifiées ;
-
les dates de diffusion des livrables servant de données d’entrées aux autres intervenants de l’étude (interface), et des autres livrables ;
-
la cohérence de l’étude avec les dates des travaux.
e) Principes de modélisation
Le but est d'expliquer les méthodes de calcul. On veillera à :
-
clarifier les principes de modélisation de la structure, les modalités de prise en compte des chargements, des combinaisons, … ;
-
justifier toutes les hypothèses simplificatrices ;
-
présenter si nécessaire des petits modèles tests validant les hypothèses ;
-
présenter l’enchaînement des calculs.
Chapter C. Good practices to create a model
C. Bonnes pratiques pour monter un modèle
Les différents niveaux d’études et la complexité associée du modèle ont déjà été définis avant l’étape de modélisation dans le contenu du chapitre B.
Ce chapitre C présente, en outre, les simplifications pouvant être adoptées pour créer un modèle structurellement représentatif de la conception de l’ouvrage réel, de son fonctionnement et des sollicitations qu’il subit.
C.1 Données d'entrée et unités
C.2 Modélisation des éléments principaux
C.3 Éléments finis et maillage
C.4 Modélisation des éléments non structuraux ou équipements
C.6 Connexions - liaisons - assemblages
C.8 Sections composées (poutre/dalle)
C.10 Comportement spécifique au cisaillement et à la torsion
C.12 Compléments liés aux éléments volumiques
C.13 Compléments liés aux calculs non linéaires
C.14 Compléments liés à la précontrainte
C.15 Compléments liés au calcul phasé
C.16 Compléments aux calculs dynamiques et sismiques
$translationBooksC.1 Données d’entrée et unités
C.1 Données d’entrée et unités
Test pour voir si AFGC prévenue.
Les données d’entrée doivent être cohérentes les unes par rapport aux autres, que ces valeurs soient définies dans le modèle lui-même ou bien qu’elles proviennent d’autres fichiers telle qu’une bibliothèque de profilés ou de données sortant d’un autre logiciel (*). Des éléments de méthodologie sont fournis précédemment au paragraphe B.7 Organisation du calcul.
(*) En particulier, une attention forte est à apporter aux unités et signes lors de l'introduction de matrices de raideurs modélisant les fondations ou une autre partie de la structure, surtout si elle provient de bureaux tiers n'utilisant pas le même logiciel. En plus, pour le sol, on vérifiera si ce sont des caractéristiques à long ou court terme.
Les caractéristiques des matériaux, en particulier pour le béton, doivent être cohérentes avec l’analyse menée (voir détails au paragraphe C.9).
Le système d’unités dans lequel les données sont exprimées doit être connu car celui-ci va également conditionner les unités des résultats de calculs. Mieux vaut privilégier l’utilisation des unités SI.
Il convient de veiller à la cohérence d’unités en efforts, longueurs, modules et raideurs.
$translationBooksC.2 Modélisation des éléments principaux
C.2 Modélisation des éléments principaux
C.2.1 Construction de la géométrie
La première étape de modélisation consiste à construire la géométrie du modèle par la définition des points, lignes, contours, aires et volumes. Les notions de nœuds, d’éléments et de mailles sont associées, quant à elles, aux éléments finis.
Dans certains logiciels, on peut faire une construction géométrique avant de créer les nœuds, éléments et mailles. Dans d’autres, on établit la construction géométrique en dehors du logiciel, au moyen de schémas ou de tableurs Excel, et on définit ensuite directement les nœuds, éléments et mailles dans le logiciel.
Dans tous les cas, les conventions de signes utilisées par le logiciel doivent être connues dès le démarrage de la modélisation (direction de la pesanteur dans le repère général, convention sur le signe des moments, efforts et contraintes).
Quelques notions générales :
-
Nœuds : leur présence est indispensable au niveau des appuis, à l’emplacement des joints et aux lieux de rupture de géométrie. Selon le logiciel, leur présence peut être nécessaire également aux emplacements choisis pour l’extraction des données. On se référera au § D.3.2 sur ce sujet. Selon le logiciel, il faut également prévoir un nœud aux emplacements d’introduction des charges. Enfin, selon le phénomène que l’on veut quantifier, par exemple pour des calculs en grands déplacements ou dynamiques, on est amené à devoir définir des nœuds intermédiaires sur les poutres pour bien le représenter. La définition des points de la géométrie intègre tous ces besoins de nœuds. Le nombre de nœuds doit toutefois être limité autant que possible de façon à ne pas alourdir le modèle ;
-
Eléments structurels : dans la plupart des modélisations hors volumique (barres, plaques, coques …), les éléments seront modélisés au niveau de leur fibre moyenne. C’est la méthode la plus sûre pour la bonne transmission des efforts entre les éléments et la prise en compte d'effets secondaires. Dans le cas de poutres pour lesquelles les charges sont localisées sur une face en particulier (hourdis de pont par exemple), il est loisible de définir l’élément au niveau de cette face et de procéder à un excentrement, si le logiciel ne le fait pas automatiquement. Le positionnement de la fibre moyenne des éléments désaxés est abordé au § C.7 Excentrements. Dans le cas des poutres de hauteur variable, la fibre moyenne n’est plus rectiligne et conduit à des repères locaux d'inclinaisons différentes, ce qui peut compliquer l’exploitation des résultats. Si l'on ne cherche pas à prendre en compte l'effet de voûte, on peut simplifier le modèle en conservant une fibre neutre rectiligne.
-
Voir également les exemples de calcul de grillages de poutres pour lesquels des simplifications peuvent également être admises (Lien vers les exemples).
C.2.2 Degré de simplification : trémies et évidements
Suivant la phase d’étude et le type de calcul mené (par exemple une stabilité ou une descente de charge), on ne modélisera pas forcément toutes les ouvertures.
Cas du bâtiment.
Pour les bâtiments, dès lors qu'elles sont prises en compte, il est conseillé, autant que possible, d’intégrer à la géométrie les trémies de taille non négligeable et pouvant remettre en cause le comportement de la structure (a minima dans les éléments de contreventement). Cette dernière sera découpée en fonction des intersections voiles/voiles, voiles/planchers, trémies, de façon à avoir un maillage le plus régulier possible.
Dans le cas de la modélisation d’un bâtiment, la définition des trémies est effectuée en fonction :
-
de leur taille (toute trémie dans un voile ou une dalle dont la plus grande dimension est inférieure à 1 m est couramment négligée) ;
-
de leur groupement spatial - des ouvertures de petites dimensions mais très rapprochées peuvent être considérées comme une seule ouverture dont les dimensions correspondent au périmètre de l’enveloppe ;
-
de leur influence sur le transfert d’efforts.
Une attention particulière doit être portée sur les linteaux des portes des voiles porteurs (et de contreventement), en effet ces linteaux sont généralement percés par de nombreuses réservations, ils peuvent alors ne plus être capables d'assurer leur rôle structurel, ce qui nécessite une modélisation adaptée.
Lorsque les réservations ne sont pas connues, les modélisations des bâtiments soumis à des efforts horizontaux (vent, séisme) doivent prendre en considération des mesures conservatoires concernant les grosses trémies (de ventilation généralement). Il est souvent nécessaire de réduire fictivement l'épaisseur des linteaux, voire de les supprimer des modélisations.
Exemple de regroupement d'ouvertures :
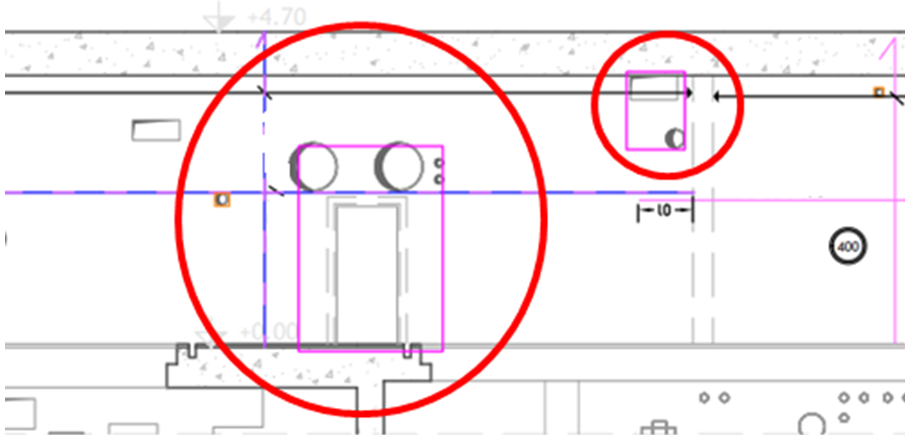
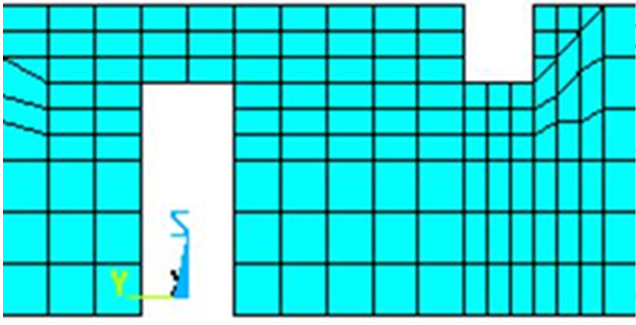
Exemple de structure avec des trémies conséquentes… qui ne peuvent clairement pas être négligées.

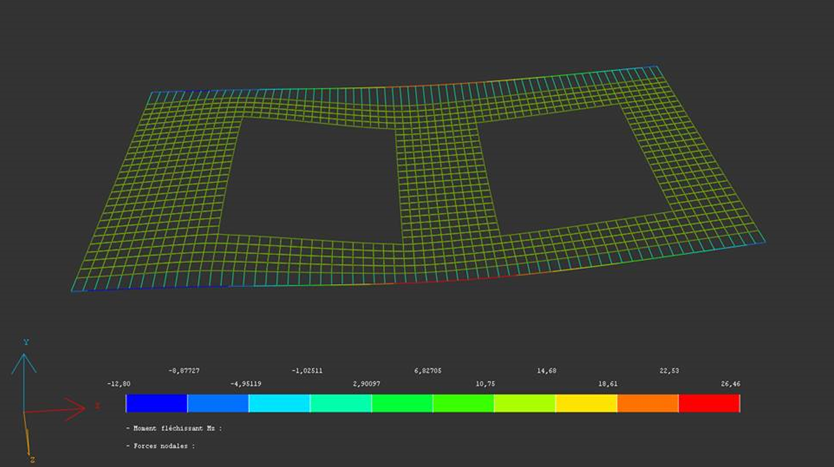
Cas de la construction métallique. Les recommandations de la CNC2M pour le dimensionnement des poutres en acier avec ouvertures dans l’âme selon la NF EN 1993 précise qu’une ouverture isolée présentant une dimension maximale inférieure à 10% de la hauteur de l'âme de la poutre n'est pas considérée comme significative. D’un point de vue modélisation de ces ouvertures, la même règle peut être appliquée. Néanmoins, cette ouverture doit être prise en compte lors de la vérification de la section selon les règles habituelles de la NF EN 1993.
Dans le cas d’un dimensionnement avec collaboration de paroi, avec des diaphragmes constitués de plaques nervurées, conformément à l’EN 1993-1-3 § 10.3.4, des ouvertures de petites dimensions, régulièrement réparties, dont la surface cumulée représente jusqu’à 3% de la surface totale peuvent être disposées sans calcul particulier du diaphragme sous réserve que le nombre total de fixations des panneaux constituants le diaphragme soit respecté. D’un point de vue modélisation, de telles ouvertures peuvent donc ne pas être prises en compte.
C.2.3 Degré de simplification : courbure, dévers, …
Au stade de la modélisation de la géométrie, à l'échelle d'un élément structurel, les éléments courbes devront être représentés de façon aussi précise que possible, sachant que l’étape du maillage discrétisera ces courbures par une succession de segments droits, en fonction de la taille de maille choisie et des nœuds déjà définis. La partie des Eurocodes NF EN 1993-1-6 traitant de la résistance et de la stabilité des structures en coque donne quelques indications sur la prise en compte de la courbure.
Pour les ouvrages d’art il convient de s’interroger sur les effets du dévers, de la courbure et du biais et leur non-prise en compte doit être dûment justifiée. Pour les ouvrages rectilignes courants, le dévers étant normalement limité lors de la conception, il est généralement possible de le négliger. En revanche pour les ouvrages d’art courbes :
-
en fonction du niveau des appuis et du degré hyperstatique de l’ouvrage, le dévers ne peut être négligé ;
-
que l’ouvrage soit courbe sur toute ou partie de sa longueur, la force centrifuge et le dévers doivent être pris en compte. Il est à noter que pour la force centrifuge, la norme NF EN 1991-2 indique que la force centrifuge, effets dynamique inclus, peut être négligé si le rayon de courbure en plan de la chaussée est supérieur à 1500 m ;
-
la courbure et le biais créent des moments de torsion non négligeable dans la structure même lorsque le chargement routier est centré transversalement sur l’ouvrage.
Pour fixer un ordre de grandeur, on peut considérer qu'un ouvrage est peu sensible:
-
au biais, lorsque celui-ci reste supérieur ou égal à 70 grades ;
-
à la courbure, quand l'angle entre deux appuis adjacents est inférieur à 0.3 rad.
Il est cependant difficile d'édicter des règles générales et le lecteur est invité à consulter les guides de conception propres à chaque typologie d'ouvrage (PRAD, PIPO, PICF, …).
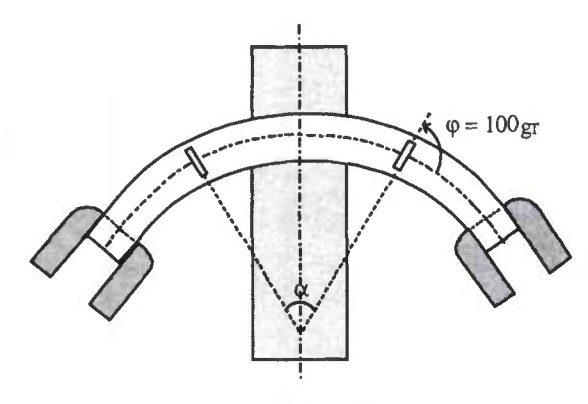
Illustration de l'ouverture angulaire entre deux appuis
L'exemple de grillage de poutres "Modélisation d'un même ouvrage suivant différentes approches" (en Partie 3) illustre les effets du biais et du dévers sur un exemple de ponts à poutres.
C.2.4 Degré de simplification : alignement des voiles d’épaisseur variable
Dans le cas d’un bâtiment, les règles de l'art préconisent un alignement des éléments verticaux de façon à assurer une descente de charges simple. Toutefois, des exigences diverses (équipements abrités, espace disponible…) peuvent amener à certains décalages d’un niveau à l’autre. Une simplification de la géométrie lors de la modélisation peut cependant être faite (notamment afin d’éviter un maillage trop hétérogène) par alignement des éléments verticaux et même des éléments horizontaux.
Cette simplification aboutit à une bonne représentation du fonctionnement global de la structure, sous réserve du respect des dispositions constructives recommandées. Il faut toutefois faire une vérification locale du bon fonctionnement du transfert des efforts et réintégrer les excentrements réels dans cette vérification locale.
De même, pour les structures métalliques, en présence de semelles ou de tubes d’épaisseur variable (viroles par exemple), il est d’usage d’utiliser un plan moyen unique.
Par exemple, un réservoir composé de viroles ayant des hauteurs et des épaisseurs différentes sera modélisé par des surfaces cylindriques présentant :
-
un rayon identique égal à un rayon moyen équivalent ;
-
les épaisseurs appropriées selon la hauteur (épaisseur des viroles).
La valeur du rayon moyen équivalent peut être définie d’après le Guide Séisme Réservoirs de stockage DT108 qui donne des exemples de détermination d’une épaisseur uniforme équivalente, ce qui permet de définir la valeur du rayon moyen équivalent = Rayon interne de la virole + Demi-épaisseur uniforme équivalente (voir exemple ci-après) :
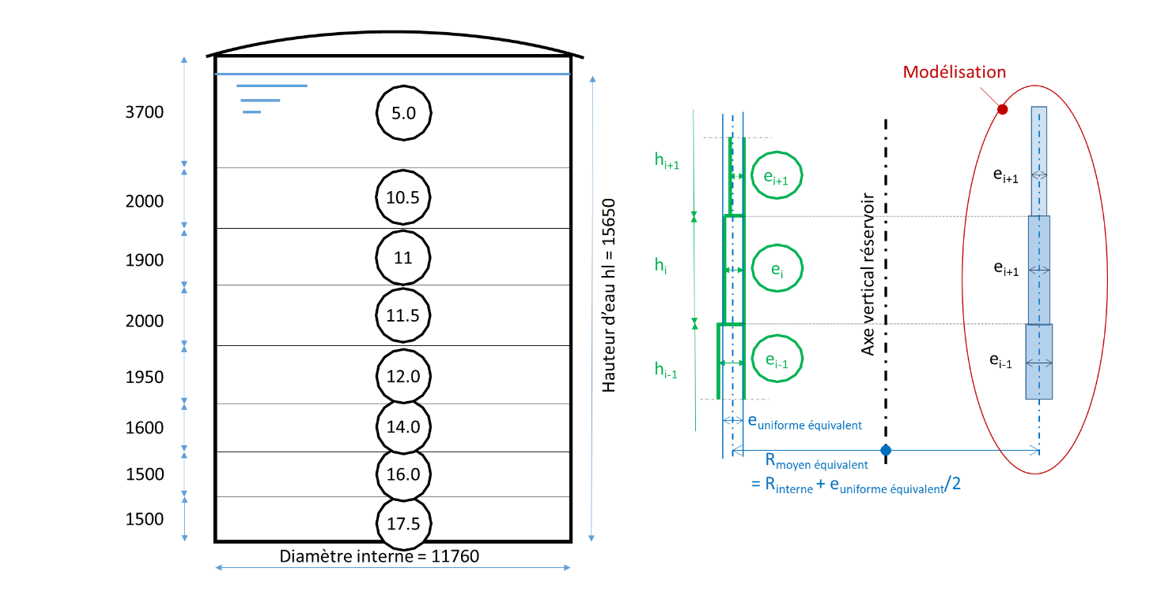
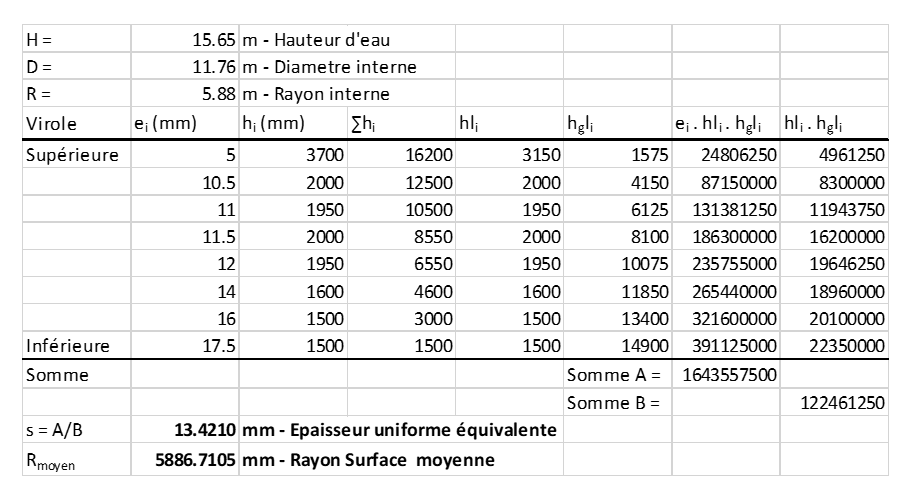
C.2.5 Utilisation de la symétrie
Comme évoqué dans la Partie 1 A2. Dimensionnalité de la modélisation, dans le cas où la structure présente, dans sa géométrie, un plan ou des plans de symétrie, il peut être très intéressant, pour limiter les temps de calcul et la taille des modèles, d’utiliser cette symétrie, en ne modélisant qu’une partie de la structure et en définissant des conditions appropriées aux limites sur le plan de symétrie.
On prêtera cependant une attention au fait que le chargement doit aussi être symétrique et que la solution obtenue sera symétrique (par exemple, les modes propres antisymétriques n’apparaîtront pas).
Exemple 1 : Pont à 4 travées, symétrique
Les travées font 60/100/100/60 m. Le pont est symétrique par rapport à son point médian.
On pourrait être tenté de modéliser la moitié du pont, en plaçant une condition d’appui de symétrie en ce point (à droite sur la figure, translation verticale bloquée, rotation bloquée) :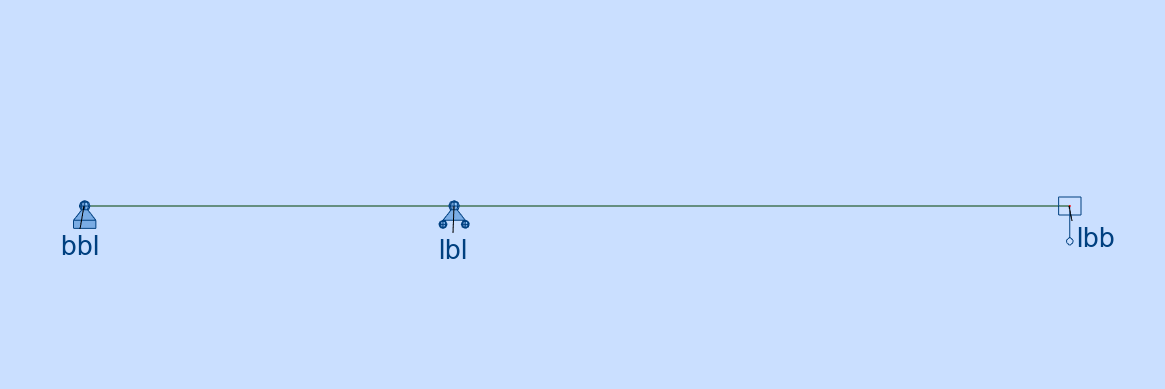
Cas de charge symétrique :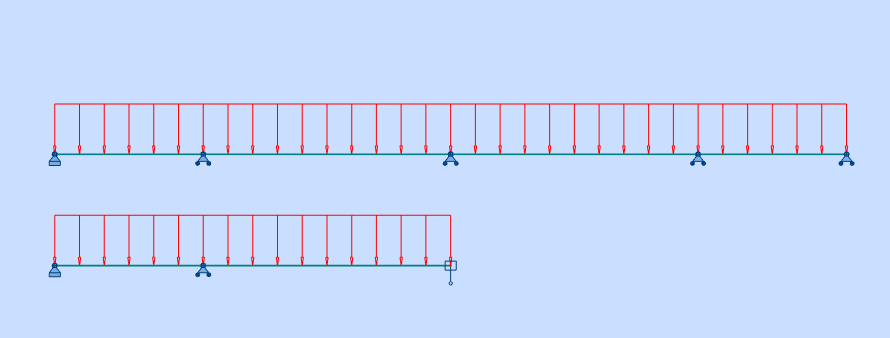
Dans ce cas, les résultats sont identiques pour les deux structures.
Cas de charge dissymétrique :
Dans ce cas, on note un écart notable dans les résultats :
L'examen des lignes d’influence du moment sur le second appui dans les deux configurations fournit une explication immédiate :
Exemple 2 : Radier
Radier de forme carrée, modélisé par des éléments coque.
Les nœuds possèdent 6 degrés de liberté (ux, uy, uz, rx, ry, rz).
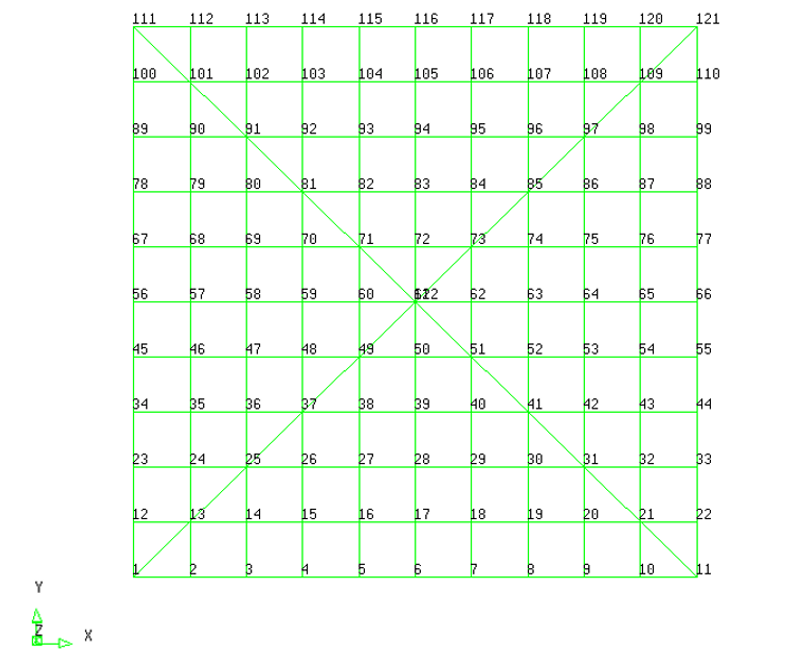
Par sa forme, il présente des plans de symétrie. Nous proposons de faire passer un plan de symétrie comme indiqué sur la figure ci-après :
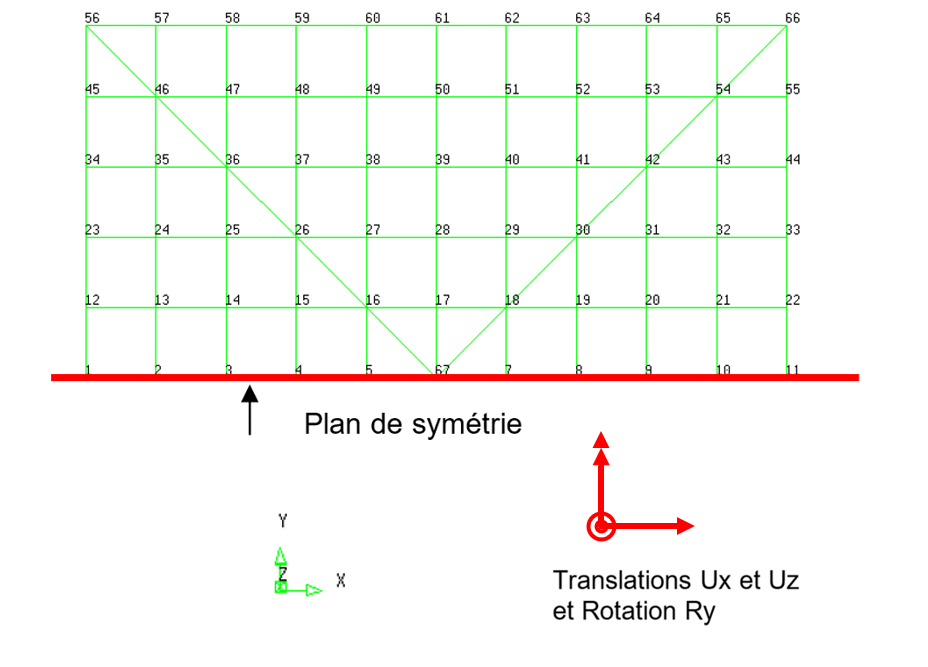
Le radier peut alors être soumis à un chargement qui est soit symétrique, soit antisymétrique.
Par exemple :
-
si l’on applique un moment autour de l’axe Y, le chargement est symétrique ;
-
par contre, si l’on applique un moment autour de X dans le sens direct, le radier bascule en montant du côté des nœuds Y>0 et en descendant du côté des nœuds Y<0. Le chargement est alors antisymétrique.
Les conditions à appliquer aux nœuds situés sur le plan diffèrent.
Dans le premier cas, les nœuds situés sur le plan de symétrie seront :
-
libres suivant les translations ux, uz et la rotation autour de y ;
-
bloqués suivant la translation uy et les rotations autour de x et de z.
Dans le deuxième cas (chargement anti-symétrique), les nœuds situés sur le plan de seront :
-
bloqués suivant les translations ux, uz et la rotation autour de y ;
-
libres suivant la translation uy et les rotations autour de x et de z.
Il est important de noter que la prise en compte des différents types de chargements conduit, dans le cas présent, à réaliser deux modèles se différenciant uniquement par les conditions aux limites associées aux chargement, ce qui n’est pas rédhibitoire.
Dans le cas de calculs dynamiques représentant un bloc de sol, on prêtera une attention particulière aux conditions aux frontières latérales du bloc pour traduire correctement les conditions de non-réflexions des ondes (voir Partie 1, chapitre F.8). La définition de ces éléments couplant un ressort et un amortisseur sortent du cadre de ce guide.
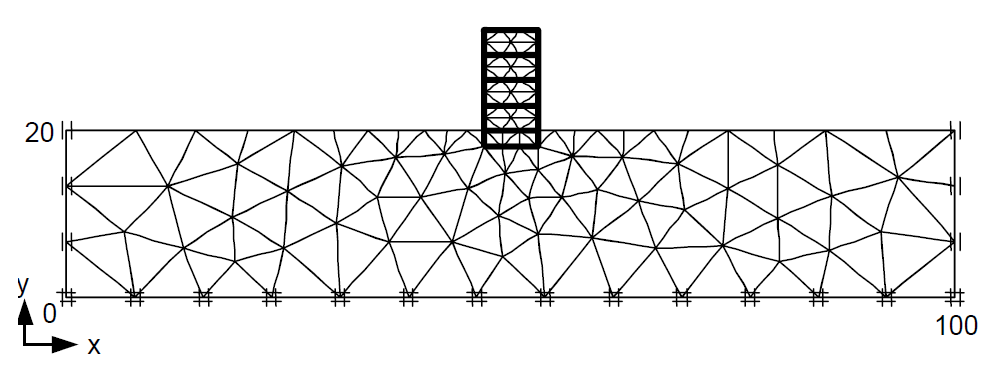
© doc Plaxis
C.2.6 Modélisation des fondations
La plupart du temps, le sol est représenté dans les modèles par des conditions d’appui (appuis simples ou encastrements).
Avant de modéliser les fondations et le sol en détail, il faut évaluer la sensibilité de la structure vis-à-vis de la souplesse de ses fondations.
Si la structure y est sensible, on doit prendre en compte le sol :
-
soit indirectement par des appuis élastiques ou des matrices de raideur, dont les paramètres auront été calibrés par ailleurs.
-
soit directement en modélisant un certain volume de sol (blocs de sol + éléments frontière). A noter que ce type de calcul nécessite des logiciels particuliers.
Dans le cas où la fiabilité des paramètres de sol est faible et/ou leur variabilité forte, il est recommandé d'effectuer un calcul en fourchette.
Dans certains cas, le fait de devoir modéliser la structure avec ses fondations relève d’une obligation règlementaire. Se référer à la norme NF-EN-1998-5 §6.
Pour plus de détail sur les conditions aux limites, on se référera au § C.5 Conditions aux limites.
C.2.7 Modélisation des contreventements par barres
Piège! Dans le cas des structures métalliques, certains éléments très élancés (contreventements ou câbles) ne peuvent travailler qu’en traction. Si la modélisation n’en tient pas compte, la résistance et la raideur du contreventement sont surestimées, aussi bien pour les calculs statiques que modaux.
Illustration par l'exemple sur une structure simple contreventée
Modélisation « tel que construit », avec des barres croisées, mais sans tenir compte du fait que les barres de contreventement vont flamber dès qu’elles vont être mises en compression :
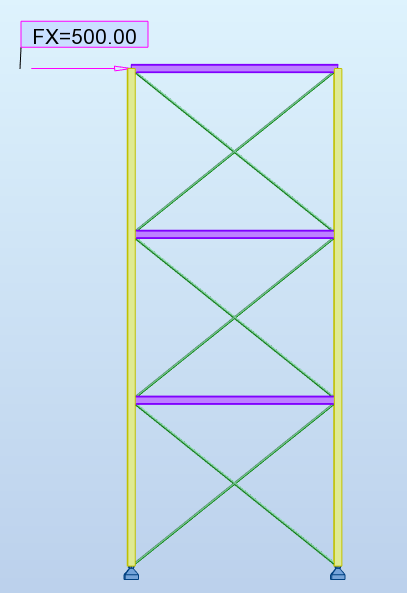
Dans ce cas :
-
la flèche horizontale vaut 4.4 cm ;
-
l’effort dans les diagonales maximal vaut 321 kN.
Du fait du flambement des diagonales comprimées, pour le comportement global, il faut supprimer une diagonale sur deux, idéalement celles qui sont comprimées mais ce n’est pas une obligation :
Dans ce cas le déplacement passe de 4.4 à 7.6 cm. La raideur de cette palée est donc divisée par 7.6/4.4=1.73, avec toutes les conséquences que cela peut avoir sur la vérification des déformations et les calculs de périodes propres pour le calcul sismique (Erreur de l’ordre de 1.730.5=1.31).
De manière corollaire, les efforts dans les diagonales passent de 321 à 641 kN, soit également de l’ordre du double, en toute logique.
C.2.8 Zoom structurel – Modèle local
Pour des problématiques de fonctionnement local d’un élément ou d’un assemblage d’une structure, il peut être intéressant de bâtir un modèle très local, en lui imposant des conditions aux limites qui reproduisent l’interaction avec le reste de la structure.
C’est par exemple le cas des entretoises de tabliers mixtes, des zones d’appuis des ouvrages complexes ou des encastrements arc/tablier dans un bow‐string.
Il arrive parfois que l’ouvrage soit modélisé dans sa globalité à l’aide d’éléments poutres sauf une partie modélisée à l’aide d’éléments plaques. Dans ce modèle intégrant des éléments de type poutre et plaque, il convient de vérifier attentivement que la transmission des efforts de l’un à l’autre s’effectue convenablement (par exemple en s’assurant de la rigidité suffisante d’éléments fictifs de liaison). Voir C.6.7.
Modélisation globale en éléments poutres (vue pseudo-volumique)
Modélisation locale en éléments plaques (vue des surfaces moyennes)
C.3 EF et maillage
C.3 EF et maillage
C.3.1 Types d’éléments finis
Avant toute chose, l'utilisateur d'un programme EF doit veiller à la bonne compréhension du vocabulaire utilisé par le logiciel : barre/poutre, plaque/coque, surface/panneau, etc…
Une partie théorique est consacrée aux éléments finis en Partie 1 § A.3. En particulier, les différents types d’éléments y sont décrits.
L’utilisateur est invité à consulter la notice de son logiciel concernant chacun des éléments finis pour vérifier ses degrés de liberté, et les efforts et déformations qu’il prend en compte, éventuellement avec des options à activer ou désactiver.
Les questions à se poser sont les suivantes. En fonction du problème à résoudre, veut-on :
-
que l’élément travaille en efforts normaux, en flexion ou les deux ?
-
qu’il prenne en compte le cisaillement et la déformation associée ?
-
qu’il se déforme hors de son plan ou dans son plan ?
C.3.2 Forme du maillage
La première partie du présent guide (Partie 1 § A.3) a détaillé les différentes formes possibles de maillage pour les éléments surfaciques (triangles, quadrilatères) et pour les éléments volumiques, ainsi que les conditions d’utilisation de ces différentes formes.
On ne décrit ici que les règles à suivre, une fois que le type de maillage a été choisi.
La plupart des logiciels ont des mailleurs automatiques, avec parfois de nombreuses options pour améliorer et personnaliser le maillage.
Le conseil principal est de rechercher le maillage le plus régulier possible, mais de raffiner néanmoins là où cela est nécessaire.
Dans certains cas et en fonction du logiciel utilisé, il est plus intéressant de mailler manuellement. On obtient ainsi des mailles régulières, dont on peut maîtriser la numérotation, ce qui facilite l’application des charges et l’exploitation des résultats.
Il y a des règles sur l’élancement des éléments (le rapport entre la plus petite et la plus grande dimension doit être supérieur à 1/3) et sur la distorsion (respect de la planéité des éléments). Les éléments distordus peuvent nuire à la pertinence des résultats. Pour un calcul non linéaire, par exemple, si un élément très distordu au départ se trouve dans une zone à forte déformation, la distorsion de cet élément peut s’accentuer entraînant une interruption du calcul, du fait d’un dépassement des critères limites. Certains logiciels le signalent. Il y a également des règles à respecter sur les angles ou ratio d'aspect des éléments. Certains logiciels peuvent tester l'ensemble des mailles vis à vis de ce critère, le cas échéant, en le pondérant par la surface relative de l'élément fini.

Exemple de détection d'EF ne répondant pas à un critère de ratio donné
Le ratio d'aspect d'un triangle est la valeur 2Ri/Ro, où Ri est le rayon du cercle inscrit au triangle et Ro le rayon du cercle circonscrit. Cette valeur est comprise entre 0 et 1. Plus la valeur est proche de 1, meilleure est la qualité du triangle ; c'est le cas pour les triangles équilatéraux. A contrario, lorsque l'aire du triangle est nulle, le ratio d'aspect vaut 0.
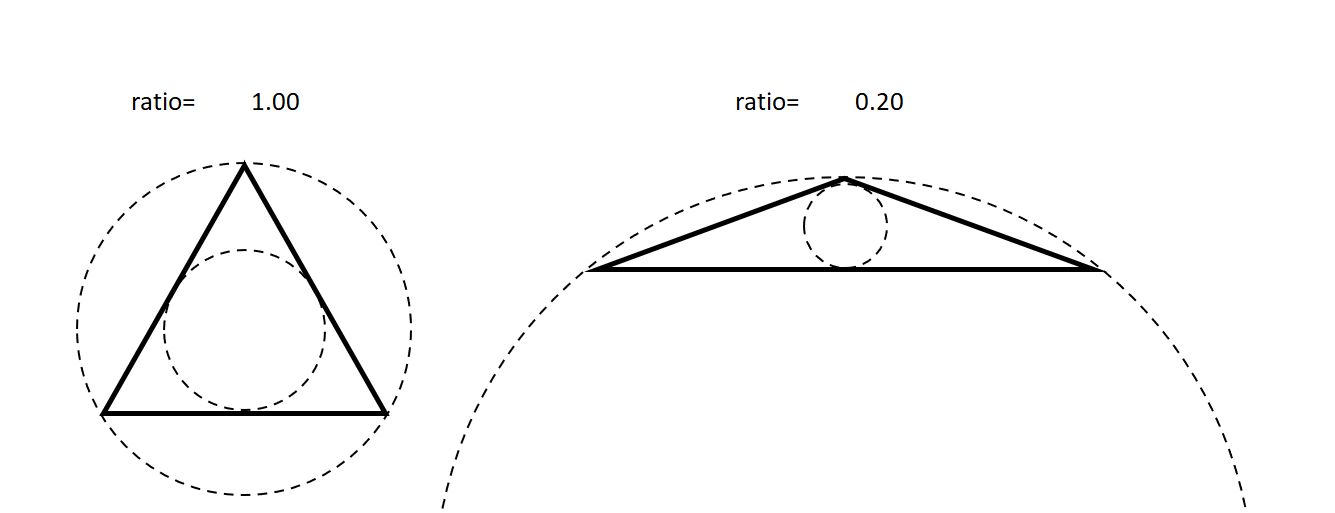
Illustration de la définition du ratio d'aspect
On peut retenir qu'un triangle est dégénéré quand son aire tend vers 0.
Dans tous les cas, il faut regarder la forme et l’allure du maillage.
Si l’allure n’est pas bonne, il est toujours possible de tester une autre option de maillage, de créer des nœuds ou de redécouper les plaques pour que le maillage s’améliore.
Le rapport entre la plus petite et la plus grande dimension d'un élément doit être supérieur à 1/3 et le ratio d'aspect doit tendre vers 1.
Exemple: soit un parallélépipède de 160x160x160 mm3 avec une face présentant un cercle. On souhaite avoir une taille moyenne de maille d’environ 40 mm sauf au centre du cercle où on désire avoir une taille moyenne de 2 mm. 1er maillage : la modélisation des surfaces est réalisée de manière élémentaire. Dans un premier, le maillage de la surface circulaire est effectué avec une taille de maillage de 2 mm. On procède ensuite au maillage des surfaces restantes avec une taille moyenne de maille de 40 mm (en général, le maillage des surfaces va s’effectuer en suivant l’ordre de création des surfaces). 2ème maillage : la modélisation des surfaces est améliorée. Le maillage est piloté en partant de la surface centrale.
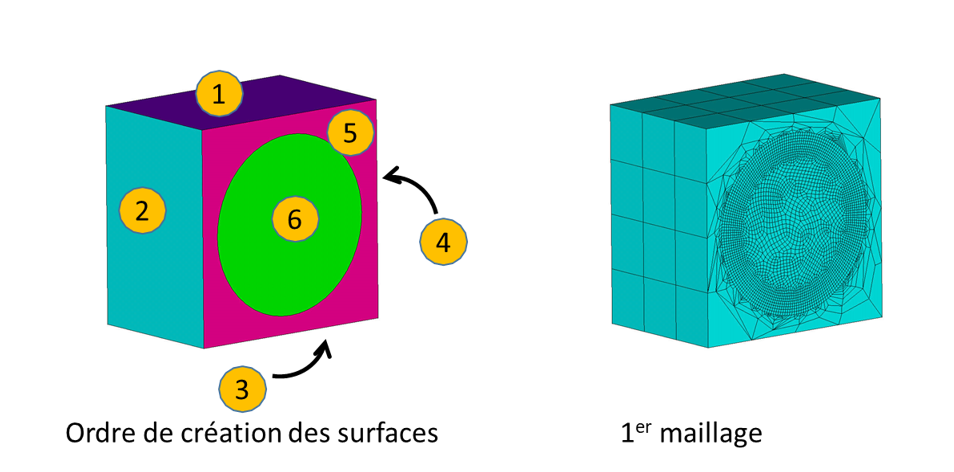
Modélisation surfacique élémentaire = Maillage non régulier + éléments dégénérés
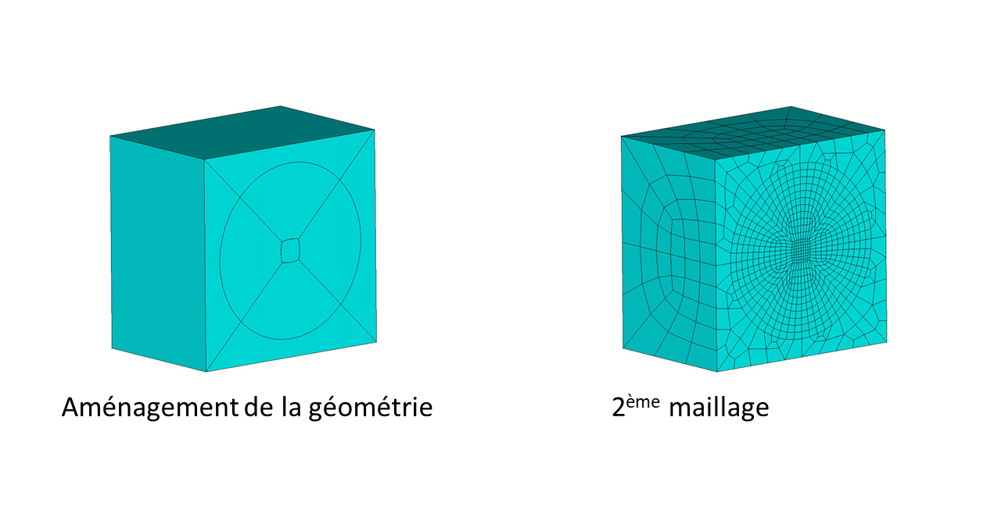
Modélisation surfacique améliorée + Maillage piloté = Maillage et éléments satisfaisants
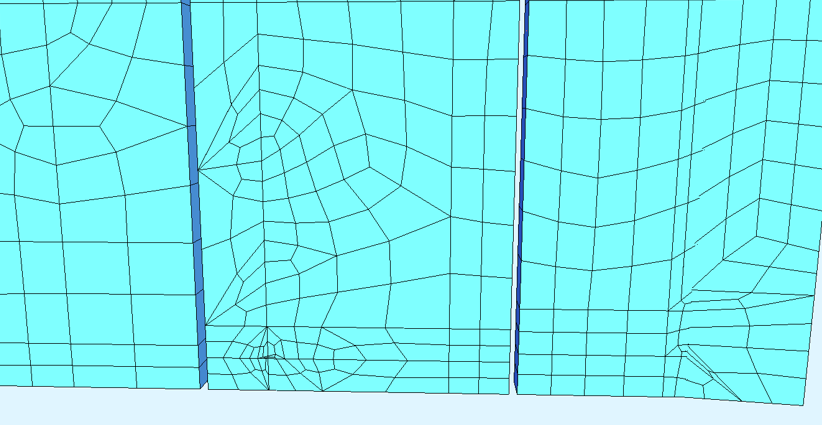
Exemple de maillage dégénéré
Un bon maillage est toujours « esthétique », il ne doit pas choquer visuellement.
C.3.3 Taille du maillage
Les objectifs des calculs doivent rester présents à l’esprit pour fixer la taille du maillage.
Tout d’abord, dans un modèle, il faut distinguer les éléments pour lesquels on veut des résultats des éléments qui sont là pour reproduire la rigidité et la masse de la structure.
Pour des éléments surfaciques et pour les éléments où l’on veut des résultats, il est d’usage de respecter une taille de maillage comprise entre 1 fois et 2,5 fois l’épaisseur de l’élément.
Pour les éléments pour lesquels on n’attend pas de résultats, on peut adopter des tailles plus grandes.
Les zones présentant un intérêt particulier dans l’analyse des résultats et susceptibles de présenter un fort gradient de contraintes et de déformations doivent donc présenter un raffinement de maillage suffisant et le moins possible d’éléments dégénérés.
Exemple d’un maillage raffiné dans les coins du bâtiment via un raffinage à partir d’un point émetteur (raffinage du maillage sur une approche concentrique) afin d’appréhender les problèmes de gradient thermique dans les planchers:
Il convient de veiller à ce que l’évolution du maillage d’un point à l’autre du modèle soit progressive. Lors du passage d’une zone à l’autre, le maillage ne doit pas présenter de variation trop brutale.
La taille du maillage doit aussi être adaptée aux capacités du logiciel et au temps de calcul disponible. Il peut s'avérer utile, avant de se lancer dans le modèle réel, de produire un modèle à la géométrie très simplifiée (voiles parallèles ou orthogonaux, absence des poutres et trémies…) et de lancer les calculs, pour vérifier que le logiciel arrive au bout - et si c'est le cas, dans un délai raisonnable - puis qu'il est capable de traiter les résultats de manière fluide, en particulier si l'on a des calculs multimodaux à produire.
Une analyse de sensibilité (en divisant ou multipliant par deux la taille de la maille et en comparant les résultats - voir paragraphe suivant sur les tests de finesse) permet de caler la taille optimale sans mobiliser des ressources superflues.
Pour les éléments filaires en calcul linéaire, le problème est moindre, car les résultats des éléments finis découlent de la théorie des poutres et ne dépendent pas du maillage. En revanche, l’affichage des résultats peut être trompeur et une règle classique est d’avoir une discrétisation de l'ordre du 1/10ème de la portée.
Pour les calculs non-linéaires, il est d’usage de raffiner le maillage à proximité des zones de plastification.
Pour la modélisation du sol, en calcul sismique, on respectera une taille de maille inférieure ou égale au 1/10ème de la longueur d’onde excitatrice (voir Partie 1 § F.8).
C.3.4 Test de finesse du maillage
Un test souvent réalisé consiste à procéder à deux calculs identiques sur le même modèle, à la différence près que pour l’un d’entre eux, la finesse du maillage est améliorée dans un rapport d'un à deux. Les résultats principaux donnés par ces deux calculs sont comparés sur les zones d’intérêts.
Cet exercice permet d’ajuster la finesse du maillage aux objectifs de l’analyse. Le temps de calcul variant exponentiellement avec le nombre de degrés de liberté du modèle, la réduction du nombre d’éléments, si elle n’induit pas de perte sur la qualité des résultats, peut être appréciable en termes de temps d’immobilisation de l’ordinateur et en termes d’espace disque nécessaire au stockage des résultats.
Inversement, il peut s’avérer nécessaire d’affiner le maillage afin que les résultats soient valides mais généralement ce raffinement ne sera réalisé que sur les zones d’intérêts.
Les indicateurs de qualité de maillage fournis par les logiciels portent sur la forme et la distorsion des éléments, et non pas sur la pertinence de la taille du maillage. Le test de finesse est donc toujours utile, notamment pour les gros modèles.
A noter l’existence de quelques rares logiciels qui disposent d’une capacité de maillage adaptatifs en fonction des chargements et des déformations (cette option est plutôt utilisée pour des calculs non-linéaires).
Illustration
Exemple de l’impact de la taille du maillage sur les résultats dans un plancher - de haut en bas, maillage de 20, 40 et 80 cm, respectivement. Le cisaillement maximal qui est égal à 0.92 MPa avec un maillage de 20 cm passe à 1.49 MPa avec un maillage de 40 cm et à 1.22 MPa pour un maillage de 80 cm.
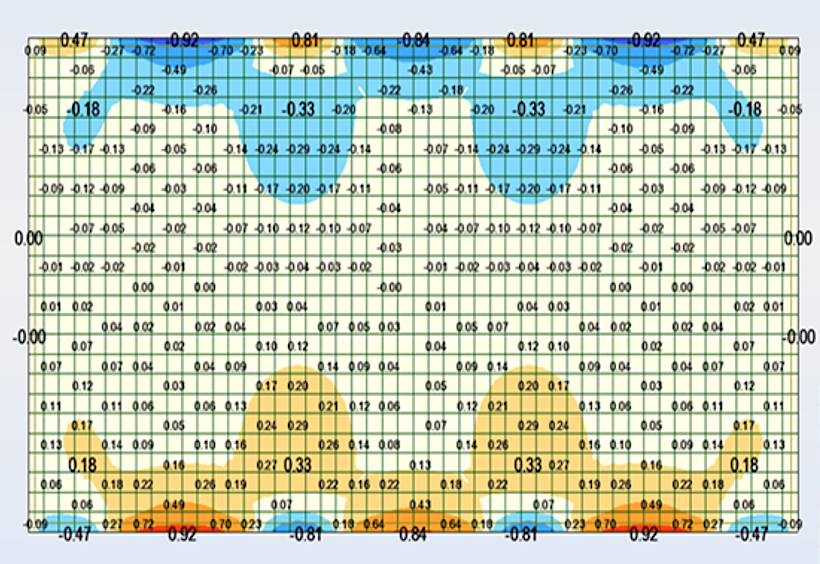
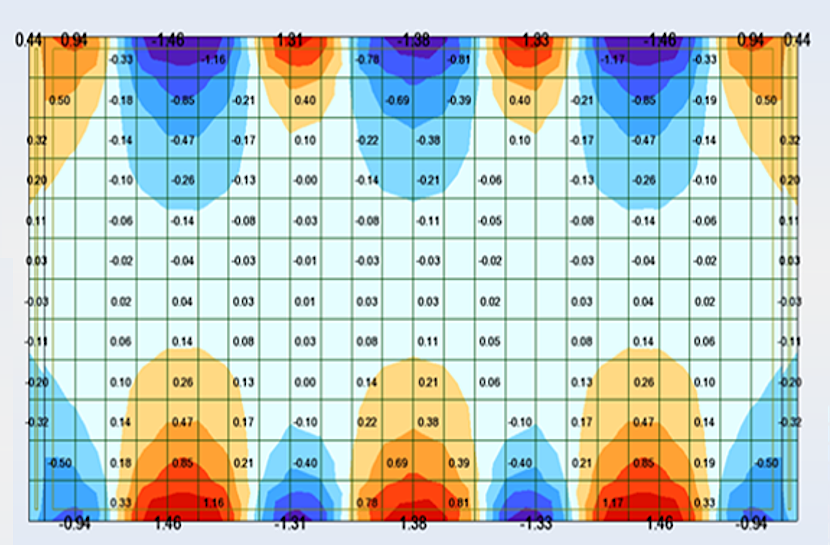
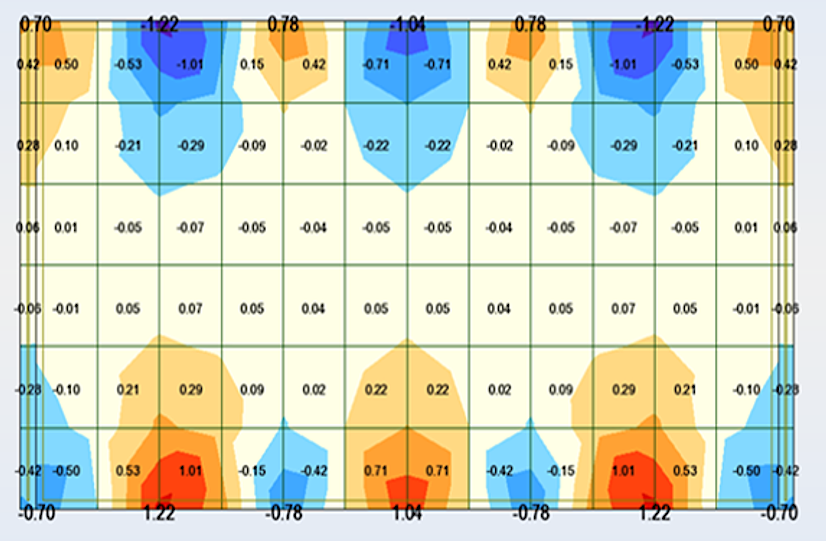
C.3.5 Orientation des repères locaux
L’orientation des éléments a une répercussion importante lors du post-traitement des résultats.
La vérification des repères locaux doit se faire de préférence avant l'introduction des chargements du modèle, ces derniers pouvant être subordonnés aux axes locaux des plaques.
Pour les éléments filaires, l’axe X des éléments de poutres est usuellement dirigé du point « origine » au point « extrémité », les axes Y et Z étant en théorie positionnés de manière quelconque par rapport à cet axe X. Or la position de ces axes Y et Z doit être homogène pour les éléments d’une même famille, d’une part pour faciliter l’application des charges transversales (par exemple une charge de vent) et d’autre part pour la lecture des contraintes en fibres extrêmes qui sont définies par translation selon Y et Z de la fibre neutre.
Dans la plupart des logiciels, les axes locaux des éléments sont orientés par défaut soit par rapport au repère global du modèle (alignement du Z local avec le Z global), soit par rapport à l’ordre de création des entités. On peut toujours forcer une orientation homogène sur un ensemble d'éléments.
Pour les éléments 2D, de la même manière :
-
la normale sortante doit être connue lors de la définition des cas de charge (pression des terres, fluides ou champs de température) ;
-
il peut être judicieux de suivre une logique de détermination de la normale sortante, à la fois pour l’entrée en donnée des enrobages dans le cas d’un calcul de ferraillage, mais aussi pour orienter au préalable l’élément en fonction de la direction supposée du ferraillage à mettre en place (ou à vérifier). On essaiera de suivre la même logique pour tout le modèle (par exemple normale ascendante pour tous les planchers) pour ne pas induire d’erreurs dans l’exploitation des résultats ;
-
une orientation uniforme permet en outre d’éviter des discontinuités dans l’affichage des contraintes pour une fibre donnée de deux tôles adjacentes par exemple.
Exemple: Plaque et repères locaux des éléments
Sujet : le sens de définition des plaques peut, pour certains logiciels, générer l’orientation des repères locaux des éléments.
Exemple : Plaque 6×6 m² (modélisée avec 2 plaques de 3×6 m²), appuyée sur 4 côtés, charge de 3 T/m²

Vue des repères locaux des éléments
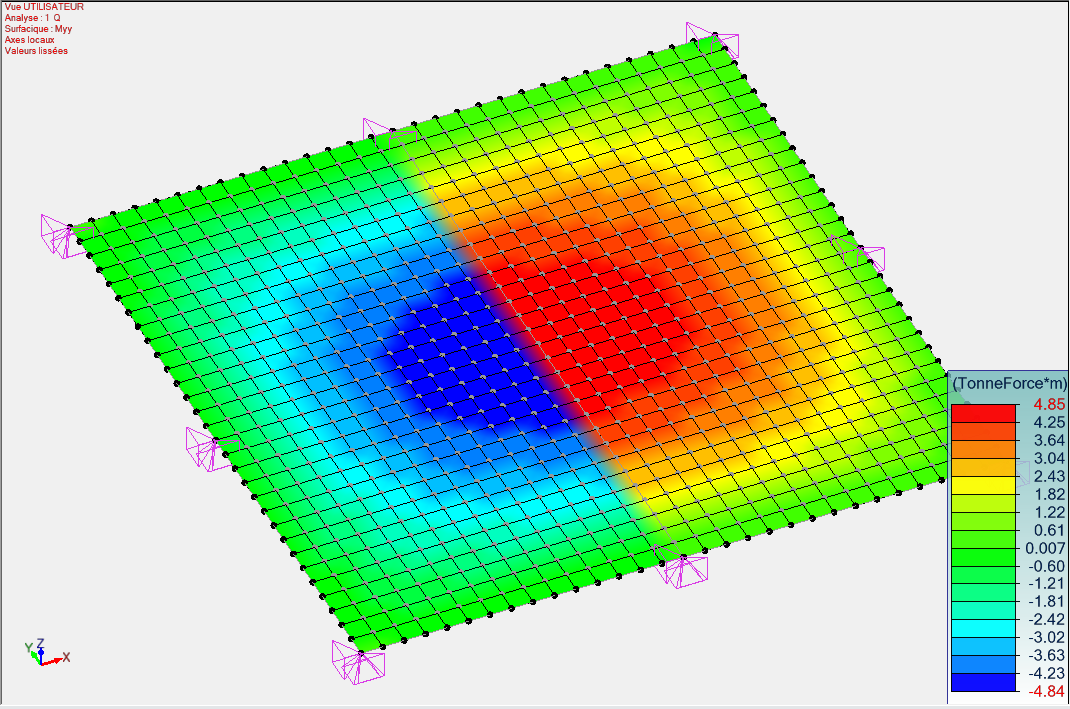
Vue des moments de flexion
On note alors une brusque discontinuité des moments sur la ligne de liaison entre les deux plaques. Cette discontinuité, qui n’a aucune origine réelle, est uniquement due à la modification d’orientation des repères locaux.
En particulier, le changement d'orientation de repères comme ci-dessus, posera problème si l'on demande au logiciel de calculer des efforts moyens dans une coupure donnée…
Vérifier que tous les repères locaux ont la même orientation.
C.3.6 Taille de modèle
Le temps de calcul est souvent déterminant dans l’économie du projet. Il est donc toujours intéressant de chercher à optimiser ce temps de calcul.
Le temps de calcul d’un modèle dépend de nombreux paramètres :
-
le nombre de degrés de liberté (nombre de nœuds x ddl) ;
-
la performance de la machine ;
-
la performance du logiciel (algorithme, parallélisation …) ;
-
la quantité de données sauvegardées (calcul temporaire non linéaire) ;
-
le type de calcul (linéaire – non linéaire).
En fonction du logiciel, on peut souvent optimiser la quantité de données à sauvegarder et le nombre de degrés de liberté.
Sur un projet courant, un modèle va tourner au moins une vingtaine de fois. Tout gain sur le temps de calcul est très vite appréciable.
Il est inutile de sauvegarder systématiquement les fichiers de résultats, en particulier si le modèle tourne en moins de deux à trois minutes. Ces fichiers ne font qu'encombrer des clouds gros générateurs de CO2.
C.3.7 Option « Merge » ou « Fusionner »
La plupart des logiciels ont des fonctions permettant de fusionner les nœuds ou les points de construction géométriques qui sont très proches en fonction d’une tolérance définie par défaut ou par l’utilisateur. Cela permet d’éviter les discontinuités de maillage.
Cette opération présente certains risques, notamment en présence de joints de dilatation ou d’absence de soudure que le modèle pourrait ignorer.
En cas de présence de joints, l’utilisateur a le choix entre :
-
représenter le joint avec sa largeur (distance modélisée entre les 2 lignes définissant les 2 bords des joints). Celui-ci est alors visible facilement lors de la manipulation du modèle et risque moins d’être « mergé » par erreur ensuite, mais cela pourra conduire à des éléments de taille hétérogène (associés à la taille du joint) si les extrémités des lignes ne se rejoignent pas ;
-
placer les points et lignes à la même position dans le modèle mais en les modélisant de façon disjointe; il est alors délicat de vérifier que le joint est bien représenté (sauf à afficher les numéros de nœuds ultérieurement) et les opérations de « merge » de nœuds doivent être effectuées avec précaution ;
-
utiliser les fonctionnalités de relâchements linéaires offertes par certains logiciels.
L’opération de fusion peut aussi impacter les asservissements entre les nœuds. C’est pourquoi les asservissements et les liens mécaniques entre nœuds doivent être définis après le « merging ».
C.3.8 Groupe d’éléments (pour la visualisation et l'exploitation ultérieure)
La plupart des logiciels offrent la possibilité de définir des groupes des nœuds ou des groupes d’éléments.
Cette fonctionnalité est très pratique et facilite l’affectation des matériaux et des masses, l’application des charges ou le post-traitement des résultats par éléments de la même famille.
C.3.9 Points de lecture des résultats et maillage
Les points de lecture des résultats découlent des vérifications à faire sur la structure. Les besoins de l’étude peuvent nécessiter plusieurs points de calcul des contraintes sur une même section (par exemple pour les contraintes normales et tangentielles).
Il ne faut pas confondre le maillage de calcul (c’est-à-dire l’ensemble des nœuds) et les points de lecture des résultats (parfois différents des nœuds).
Ce n’est pas parce qu’il y a beaucoup de points de lecture que le maillage est suffisamment précis.
Dans l'exemple ci-dessous, les multiples isolignes de moments transversaux, en particulier à proximité des appuis pourraient faire croire à une grande précision de calcul, alors que le maillage est trop large pour obtenir des résultats fiables.
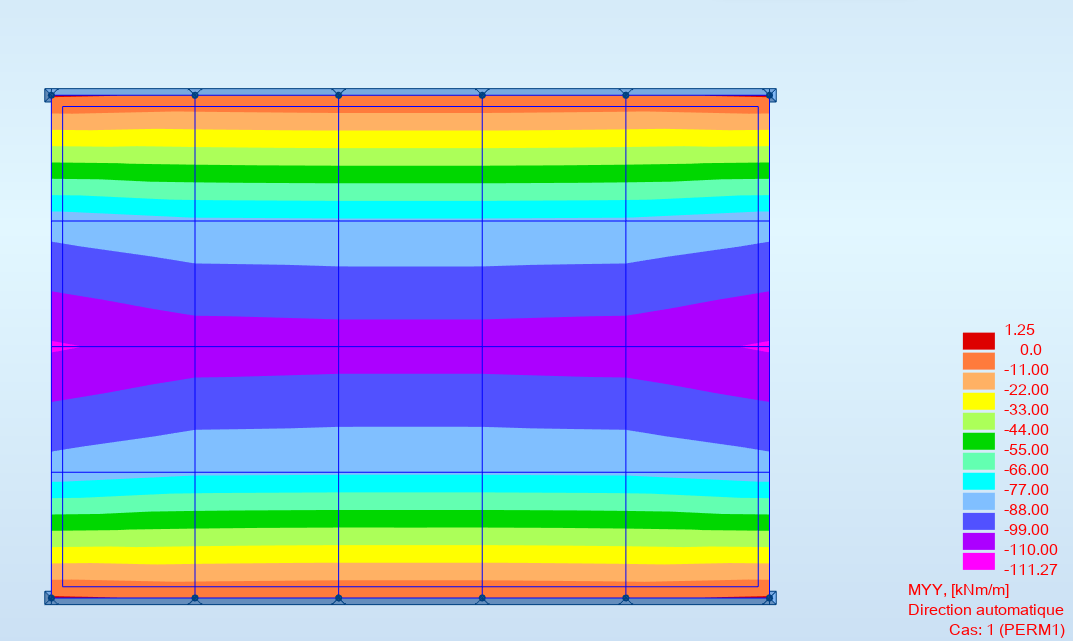
En effet, les points de lecture peuvent donner l’illusion d’un maillage raffiné alors que ce n’est pas le cas. Les résultats sur ces points de lecture étant interpolés des résultats aux nœuds.
En traçant les diagrammes de moment et de tranchant dans une coupe transversale, ceci apparaît clairement (la dalle est vue par le dessous):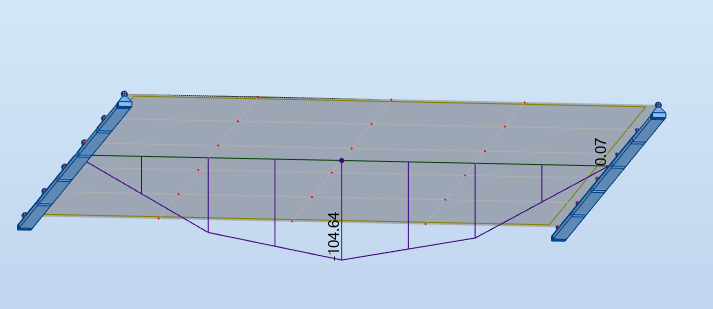
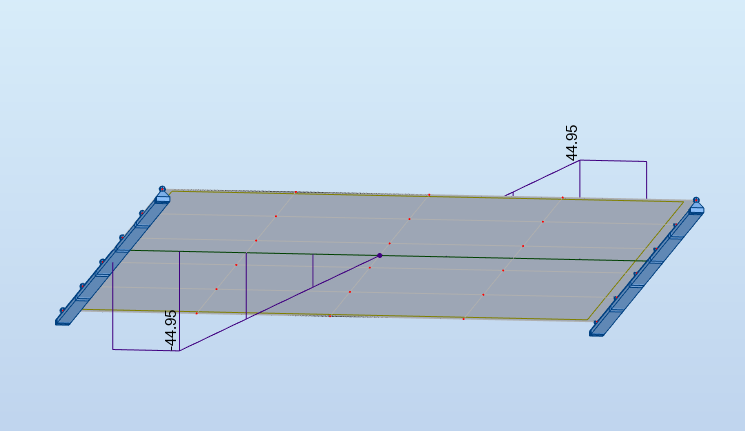
En raffinant le maillage, les graphes deviennent:

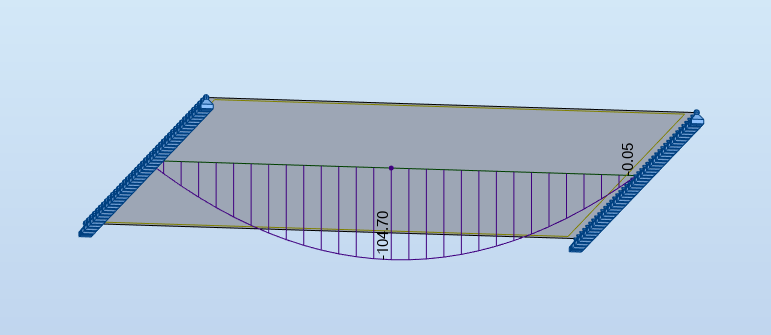
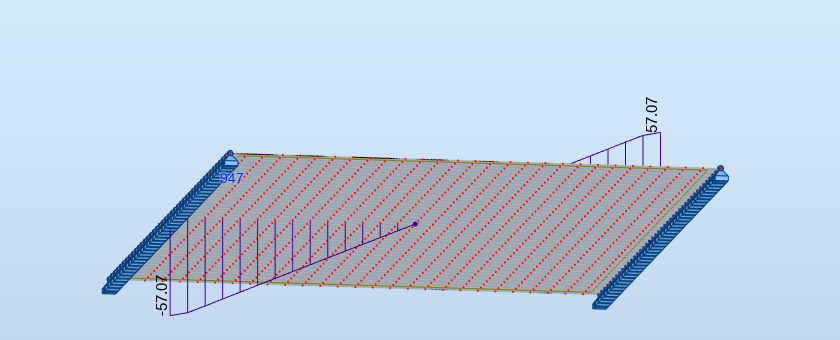
Dès lors qu'on a une singularité, ici la ligne d'appui, la taille du maillage intervient fortement dans la précision des résultats. Il suffit de raffiner le maillage pour s'en rendre compte:
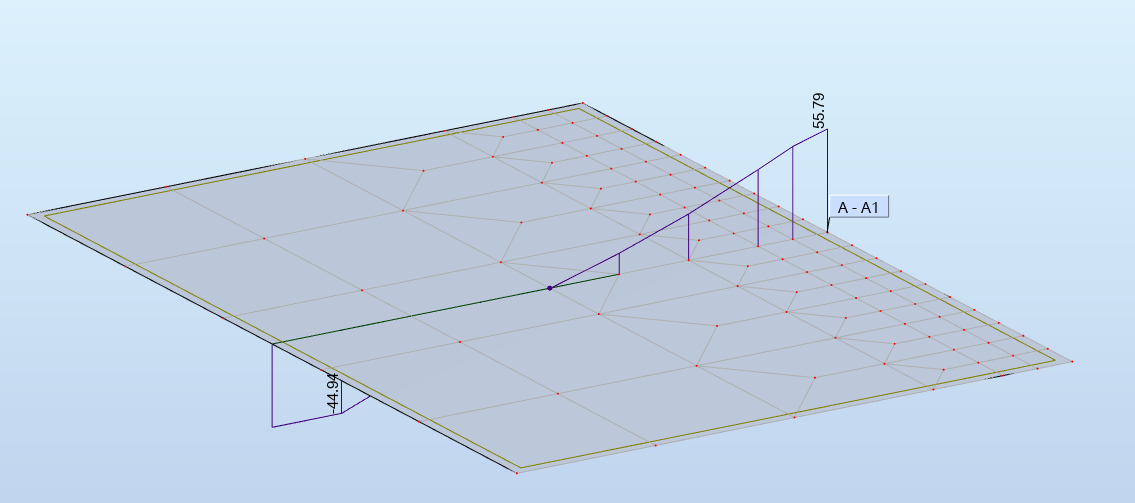
Le calcul de l'intégrale des efforts montre un impact (sur cet exemple) fort sur le tranchant (écart de 22%) et très faible sur le moment, entre la zone de maillage grossier et la zone de maillage raffiné.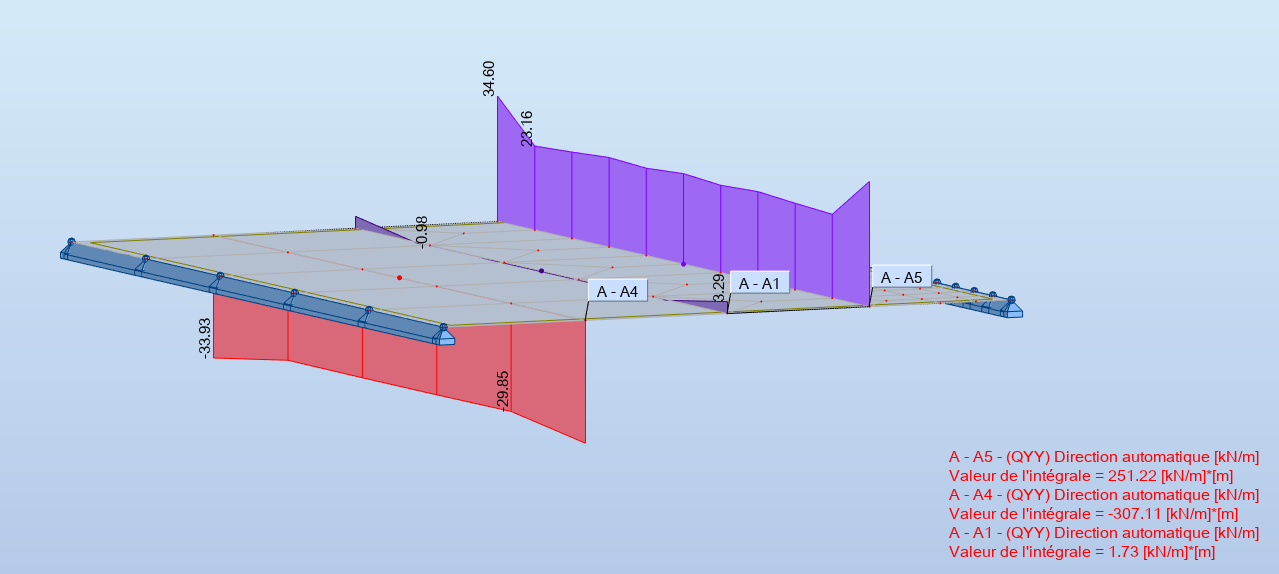
Intégrale de l'effort tranchant - plaque sur deux files d'appuis simples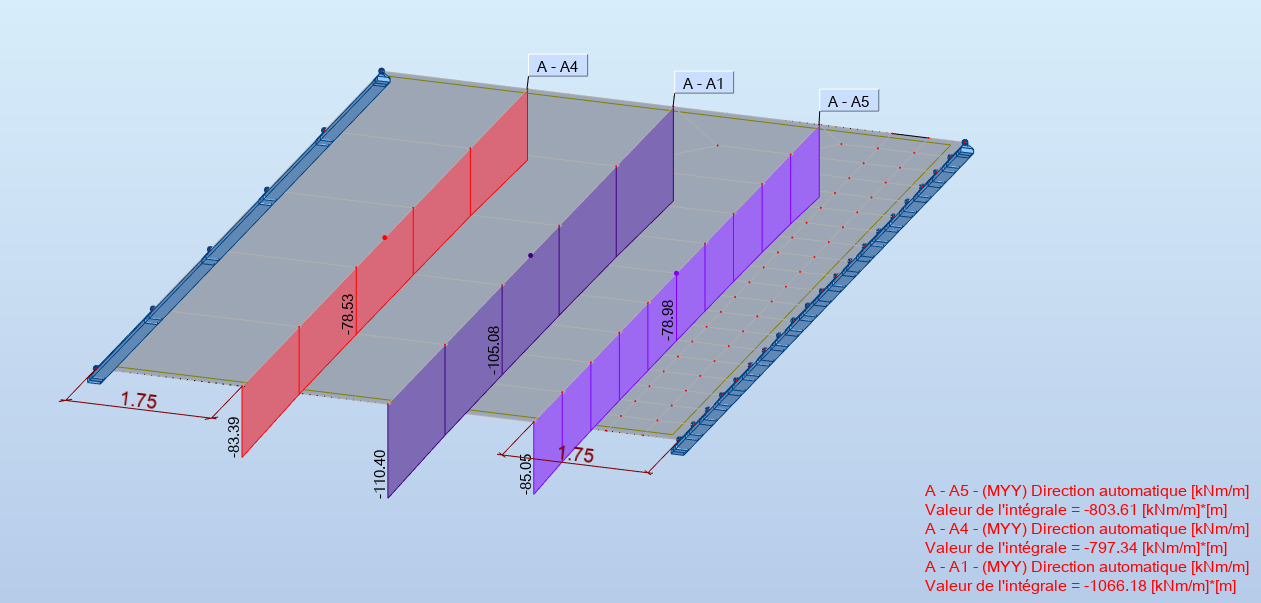
Intégrale du moment - plaque sur deux files d'appuis simples
Il suffit de créer une singularité pour le moment, en encastrant les rives, pour qu'un écart sur le moment se produise (de l'ordre de 17%)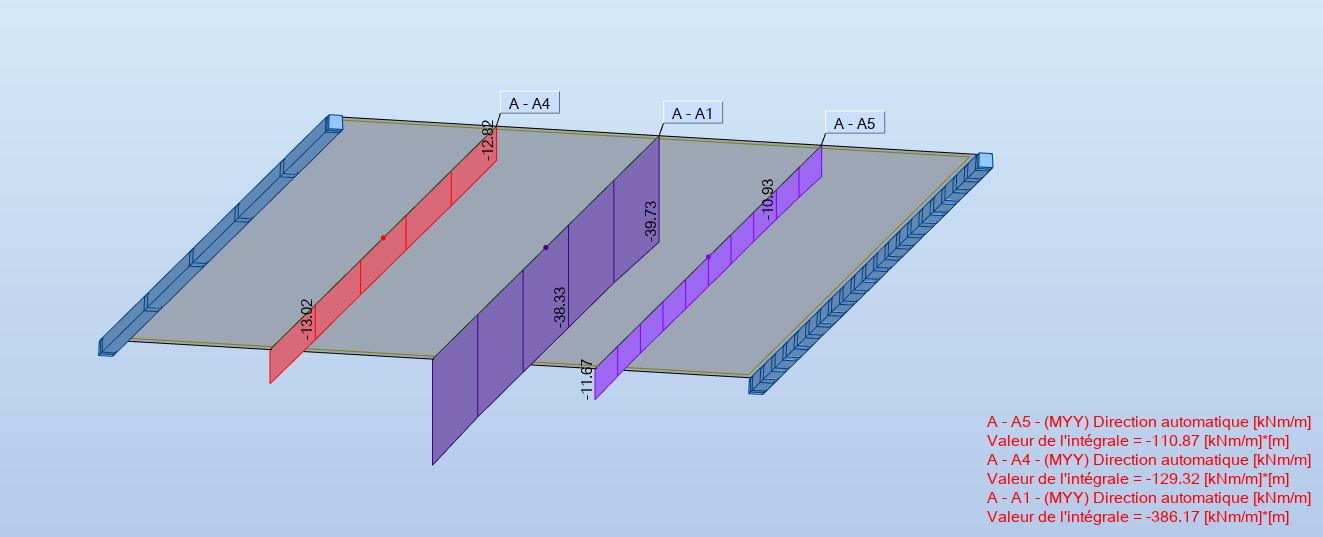
Intégrale du moment - plaque bi-encastrée
C.4 Modélisation des éléments non structuraux ou des équipements
C.4 Modélisation des éléments non structuraux ou des équipements
Les éléments non structuraux et les équipements sont des éléments qui n’assurent aucun fonctionnement structural dans le comportement de l’ouvrage. Trois cas sont à distinguer :
-
L’élément en question a une faible masse et une faible rigidité par rapport à la structure porteuse ; dans ce cas, il peut être négligé dans le cadre de la modélisation ;
-
L’élément en question a une faible masse mais sa raideur ne peut pas être considérée comme négligeable (par exemple certains panneaux de façade bridant les mouvements de la structure support). Dans ce cas, sa présence peut modifier le comportement de l’ouvrage et il est donc nécessaire de le modéliser (a minima par une rigidité fictive) ;
-
L’élément en question a une masse non négligeable mais sa raideur peut être considérée comme négligeable. Dans ce cas, une masse équivalente doit être intégrée dans le modèle.
| Équipement / Élément non structural | Masse négligeable | Masse non négligeable |
| Raideur faible | Non pris en compte | Masse à intégrer |
| Raideur non négligeable | Raideur à modéliser | Masse et raideur à modéliser |
Dans le cadre des analyses sismiques, il est important de s’assurer que l’élément ne rentrera pas en résonance avec la structure porteuse. On peut se référer aux publications suivantes pour identifier les cas pour lesquels il sera nécessaire de modéliser l’interaction élément / structure.
-
J. Betbeder-Matibet – Génie parasismique – volume 3 – Hermes Science Publications (2003).
-
FD P06-029 - Règles de construction parasismiques - Dimensionnement des ancrages en zone sismique (décembre 2017)
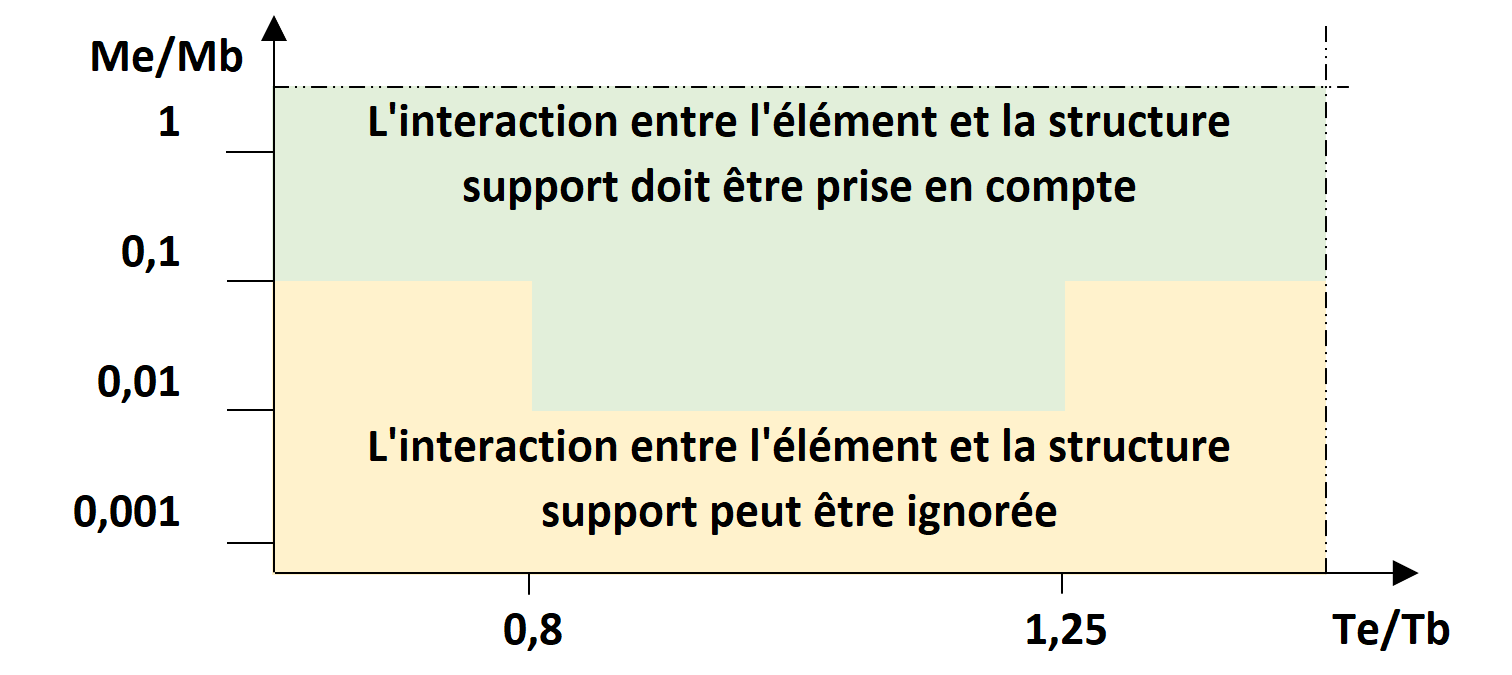
Proposition de l'AFPS sur la nécessité ou non de prise en compte de l'interaction dynamique entre élément non structural/équipement et la structure (Recommandations AFPS90, 1993).
Légende :
-
Me=masse des équipements ou éléments non structuraux
-
Mb=Masse de la structure support
-
Te= Période de l’élément non structurel
-
Tb=Période de la structure support
Nota : suivant la direction étudiée, la masse de la structure support peut se limiter au seul plancher support (pour plus de détails, se reporter aux références citées ci-avant).
Dans le calcul sismique des bâtiments, les éléments non structuraux (de type cloisons, par exemple) doivent être pris en compte dans la modélisation de la structure lorsqu’ils sont susceptibles de modifier sa raideur transversale. Ces éléments peuvent faire l’objet de justifications inspirées de celles de l’article 4.3.6 de l’EC8-1 applicable aux ossatures avec remplissage en maçonnerie.
On peut aussi être amené à supprimer des petits éléments dans un modèle destiné à une analyse modale.
$translationBooksC.5 Conditions aux limites
C.5 Conditions aux limites
C.5.1 Cas général
Les conditions aux limites sont déterminées par les degrés de liberté bloqués ou non des nœuds situés aux frontières de la structure (supports de la structure, coupures …).
Les notions de repères et de conditions aux limites sont étroitement liées ici. L’orientation d’une condition aux limites (forces, moments, déplacements imposés, accélération…) va dépendre de celle du repère actif au moment de sa mise en place et/ou de celle de l’entité (nœud, élément) sur laquelle elle vient s’appliquer.
Pour les repères, il a lieu de distinguer les repères liés aux éléments et les repères liés aux nœuds.
Généralement, par défaut, les repères liés aux nœuds sont identiques au repère global. On peut cependant attribuer à un ou plusieurs nœuds un repère d’orientation différent afin de pouvoir appliquer en ce(s) nœud(s) une condition aux limites suivant une orientation particulière. De simples contrôles graphiques de l’orientation de charges nodales (forces, moments, déplacements imposés) permettent de visualiser la bonne définition de ces repères nodaux.
Pour les éléments, les repères locaux sont liés généralement aux orientations principales définies lors de la création de l’élément. De simples contrôles graphiques de l’orientation des charges appliquées sur les éléments (pression par exemple) permettent de visualiser la bonne définition de ces repères éléments.
Les conditions aux limites doivent assurer la stabilité de la structure vis-à-vis des chargements qui lui sont appliqués et être représentatives de son fonctionnement global. Cette stabilité doit être effective systématiquement dans les 6 composantes globales X, Y, Z, RX, RY et RZ, même si les chargements ne concernent que quelques directions.
La stabilité suivant une translation s’effectue toujours par le blocage d’au moins un nœud suivant la direction de cette translation.
La stabilité autour d’un axe s’effectue soit par le blocage en rotation d’un nœud (suivant l’axe de rotation) soit par le blocage en translation de deux nœuds disposés dans un plan perpendiculaire à la rotation.
Il est important de vérifier que les réactions dans les directions bloquées uniquement pour des questions de stabilité numérique sont nulles.
Illustration :
Objectif : descente de charge d’une dalle appuyée sur 4 poteaux ;
-
La dalle est modélisée en éléments volumiques (éléments avec nœuds à 3 degrés de liberté UX, UY et UZ);
-
Conditions aux limites : blocage des nœuds aux appuis suivant la direction verticale UZ = 0.0 ;
-
Problème : certains logiciels n’effectueront pas le calcul pour des raisons d’instabilité ;
-
Conditions aux limites supplémentaires : 2 nœuds bloqués suivant la direction transversale OY + 1 nœud bloqué suivant la direction transversale OX.
Bilan :
-
4 nœuds bloqués suivant OZ - blocage vertical aux 4 appuis ce qui occasionne également la stabilisation en rotation/OX et en rotation/OY de la dalle ;
-
2 nœuds bloqués suivant OY - stabilité en translation/OY et en rotation/OZ de la dalle ;
-
1 nœud bloqué suivant OX - stabilité en translation/OX de la dalle.
On vérifiera qu’aux nœuds bloqués suivant UX et UY, les réactions RX et RY sont nulles.
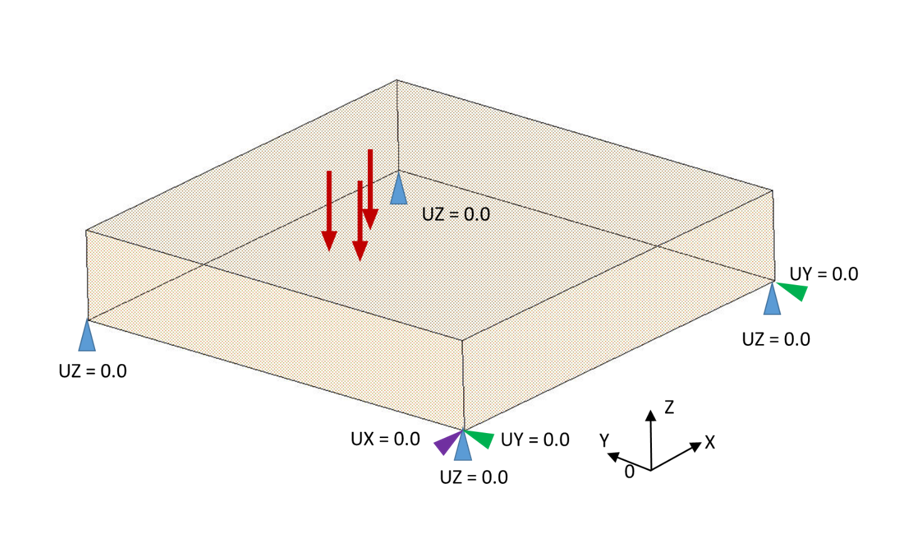
Exemple pour la stabilité minimale d’une dalle chargée en Z
Piège : la dalle n’est chargée qu’en Z, mais pour assurer la stabilité du calcul, il faut empêcher ses déplacements en translation en X et Y et en rotation autour de Z. Dans le cas présent, cela a été effectué en bloquant 2 points en Y et 1 point en X. (NB : la stabilité en Z nécessite un minimum de 3 points non alignés bloqués en Z).
Dans un modèle en 3 dimensions, un encastrement signifie que les 3 rotations et les 3 translations sont bloquées.
Dans la pratique, le logiciel peut procéder de deux façons pour le blocage des déplacements, sans laisser le choix à l’utilisateur :
-
Une méthode toujours stable numériquement, qui consiste à supprimer le ddl dans la résolution du problème, sa valeur étant nulle (voir Partie 2 – A.1 – on raisonne dans ce cas sur une matrice 5×5).
-
Une seconde méthode consistant à placer numériquement un ressort de très grande raideur dans la direction bloquée pour que le déplacement soit numériquement presque nul. (voir Partie 2 – A.1 – on raisonne dans ce cas sur une matrice 9×9 en rajoutant des termes de valeur relative très différente).
Il est important de comprendre comment le logiciel procède pour pouvoir détecter d’éventuelles instabilités numériques qui peuvent conduire à un arrêt des calculs ou des résultats non équilibrés.
C.5.2 Modélisation de différents types d’appuis
Les appuis peuvent souvent être considérés comme fixes sauf lorsque le sol intervient dans le comportement de la structure c’est-à-dire lorsqu’il existe une interaction, statique ou dynamique, entre le sol et la structure (ISS) : par exemple un sol mou générant des tassements différentiels d’appuis ou pour cerner le comportement sismique.
Les structures sont fondées sur trois types de fondations : superficielles (semelles isolées ou filantes), radiers ou fondations profondes (pieux, puits, barrettes, inclusions rigides, …).
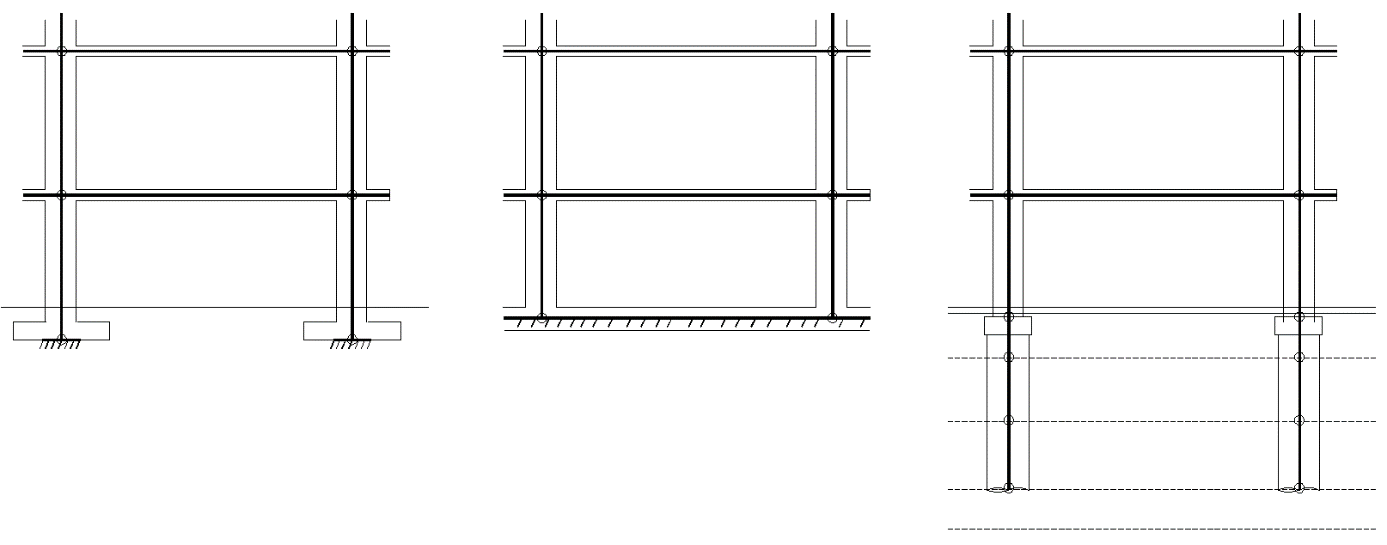
Illustration des fondations superficielles, fondations sur radier et fondations profondes.
C.5.2.1 Fondations superficielles – cas des appuis sous poteaux
Les semelles superficielles sont modélisées par des appuis ponctuels selon 3 possibilités :
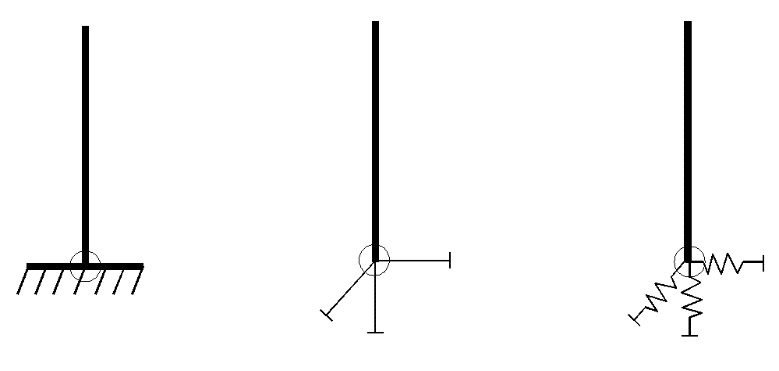
Illustration: appui encastré, appui articulé et appui élastique
Appui encastré : les 6 degrés de liberté sont bloqués.
Appui articulé : les déplacements sont bloqués et les rotations sont libres.
Appui élastique : l’appui est défini par 6 ressorts élastiques (un par degré de liberté) ou une matrice de raideur ou d’impédance.
Raideurs des appuis élastiques
Pour calibrer la raideur des appuis élastiques, il faut disposer de la raideur à l’interface entre la semelle et le sol. Cette raideur à l’interface (notée usuellement kv) est issue du rapport géotechnique.
Le terme Kz (raideur statique du ressort vis-à-vis d’un effort vertical) s’obtient par la formule Kz = kv x S où S est la surface de la semelle.
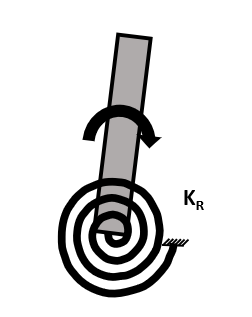
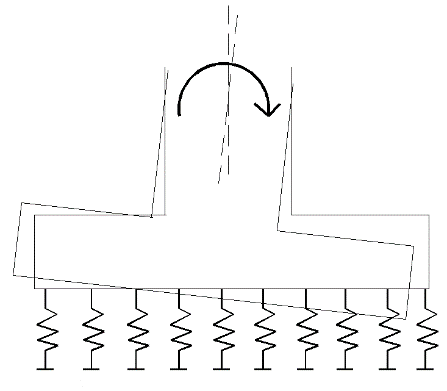
Les termes KR s’obtiennent par la formule KRi (en N.m/rad) = Ii x kv où Ii est l’inertie (en plan) autour de l’axe i de rotation de la semelle concernée.
Pour un rectangle, on va retrouver les termes Iy=b.a3/12 et Ix=a.b3/12, a et b étant les dimensions en plan.
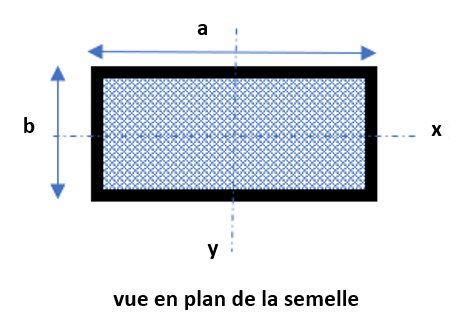
On sera vigilant à la notion de raideurs à long terme, à court terme et sismique fournies par le géotechnicien, qui diffèrent notablement.
C.5.2.2 Fondations superficielles – cas des appuis sous voiles
Les voiles sont généralement modélisés par des éléments de plaques ou coques. Deux modes de modélisation sont possibles pour l’appui.
Méthode 1 : En définissant des appuis linéiques répartis sous le voile. Ce cas se rapproche soit de celui des poteaux (voir ci-avant) en répartissant les raideurs ponctuelles linéairement sur le voile, soit de celui des radiers (voir §5.2.3 ci-après), mais en considérant une seule direction de calcul.
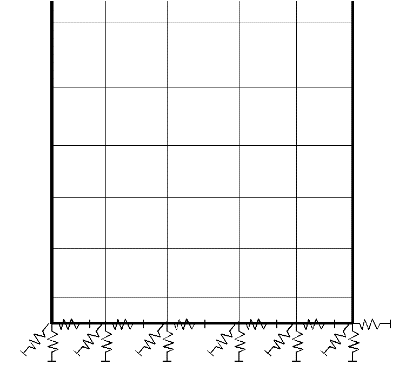
Méthode 2 : En modélisant un appui central unique pour récupérer un torseur global en pied de voile pour le dimensionnement des fondations. Une barre rigide à la base du voile est alors nécessaire pour répartir les efforts dans le voile. Les conditions d’appuis sont identiques à celles des poteaux (encastrés ou élastiques ou avec raideurs).
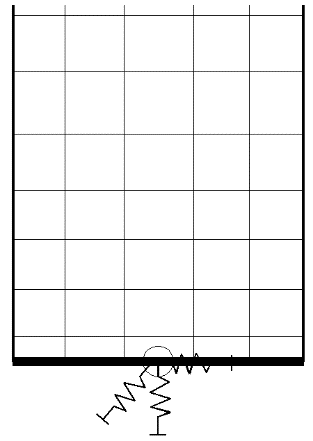
Dans les deux cas, il convient de vérifier les unités pour la raideur introduite, en cohérence avec les unités physiques fournies par le géotechnicien : s’agit-il de N/m, N/m2, N/m3 ? De même de N.m/rad ou N.m/deg ? (ou unités dérivées : kN, MN…)
C.5.2.3 Fondations sur radier
L’appui du radier sur le sol est modélisé par la mise en place de ressorts sous les différents nœuds du radier. Les raideurs des ressorts sont alors calculées selon le même principe que pour les semelles isolées. Elles peuvent être différenciées en fonction des zones de chargement. Attention à ce que la raideur soit bien proportionnelle à la surface afférente au nœud (difficulté possible en cas de maillage irrégulier, si cette affectation n'est pas automatisée dans le logiciel).
Certains logiciels proposent aussi des ressorts « surfaciques » sur plaque. Dans tous ces cas, vérifier sur un cas unitaire la bonne concordance entre effort et déplacement.
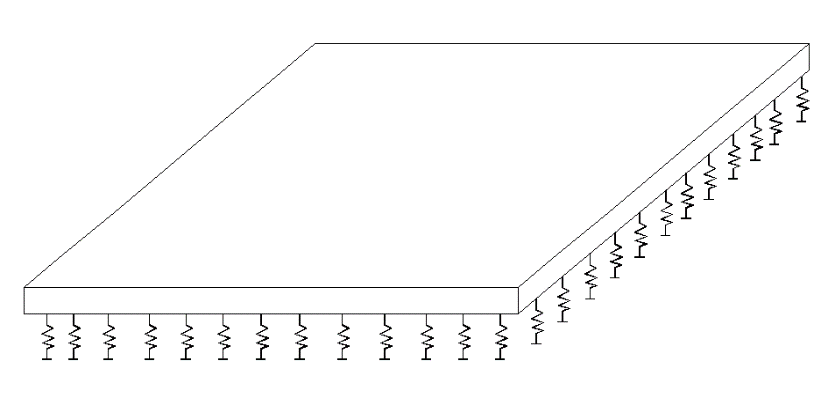
Modélisation du sol par un système de ressorts
Dans la réalité, la stabilité horizontale du radier est assurée par le frottement sous le radier et une éventuelle butée latérale. Dans la modélisation, on choisira soit des ressorts horizontaux surfaciques sous le radier, soit des ressorts sur le pourtour (ponctuels ou répartis), en fonction des vérifications internes à mener.
Attention: pour les modélisations avec ressorts surfaciques horizontaux, la raideur horizontale est en fait liée au frottement radier/sol avec des glissements éventuels. Dans le cas d’une étude de retrait, une surestimation sur cette raideur horizontale vient brider artificiellement le radier et peut générer des contraintes de traction importantes et non réalistes.
C.5.2.4 Fondations sur pieux
Les fondations sur pieux peuvent être modélisées selon 3 méthodes.
Méthode 1 : chaque pieu est modélisé au moyen d’une poutre sur sol élastique (ou appuis linéiques élastiques). les raideurs horizontales du sol dépendant des caractéristiques des couches de sol (Kx et Ky) sont généralement déterminées par le géotechnicien (attention au maillage et à la concordance des unités). Un appui vertical est positionné à la base du pieu pour représenter la raideur en pointe.
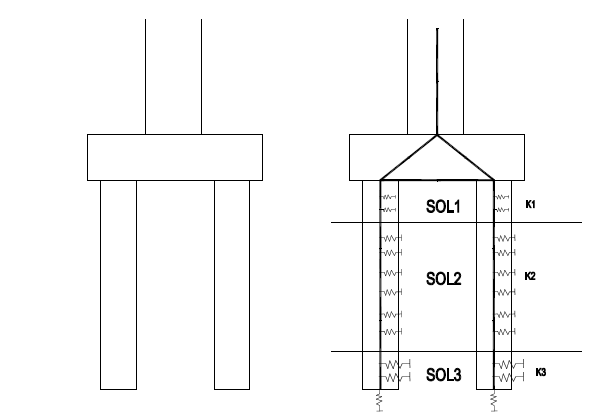
Méthode 2 (intermédiaire mais peu usitée) : chaque pieu est modélisé par un appui (ou matrice) élastique caractérisé par 6 raideurs qui sont généralement calculées par le géotechnicien.
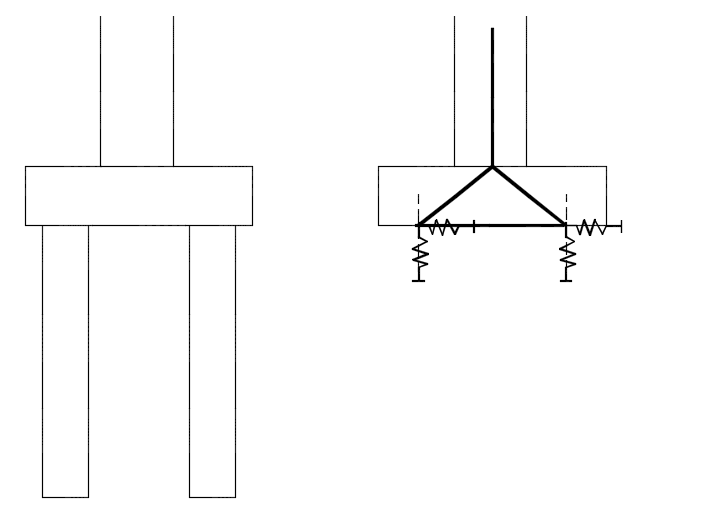
Méthode 3 : Il est possible de remplacer une fondation complexe par sa matrice de raideur ou de souplesse, qui intègre la configuration globale de la semelle avec l’ensemble des pieux.
La fondation sera modélisée dans le modèle général par un appui élastique au nœud A, dont les 6 raideurs auront été calculées au préalable à partir d’un modèle local des fondations. Voir l'exemple de calcul ci-dessous.
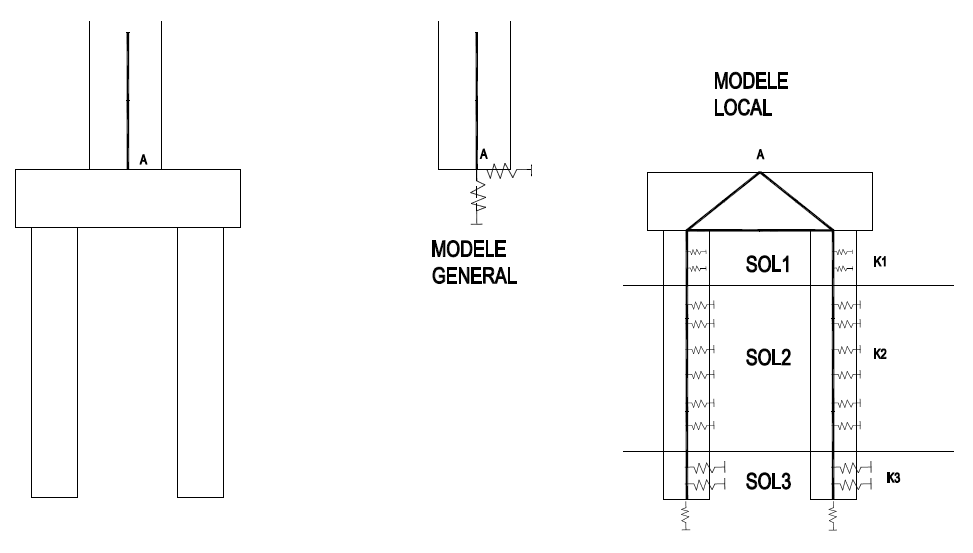
Du fait du couplage entre les déplacements horizontaux et les rotations dans les systèmes de fondations profondes, rien ne permet a priori de négliger les termes croisés (non diagonaux) de la matrice de raideur. Or très peu de logiciels permettent la prise en compte de la totalité de la matrice ; ce qui est un problème. Il convient de démontrer au cas par cas que la « diagonalisation » de la matrice n’a pas d’impact notable sur les efforts et déplacements de la structure.
Les méthodes 2 et 3 permettent de limiter la taille du modèle, surtout dans le cas de nombreux pieux. En revanche la première méthode donne directement les efforts dans les pieux.
Plus généralement, dans les modèles globaux, on modélise les pieux ou groupes de pieux par des ressorts (méthode 3). Ce n’est que pour le dimensionnement des pieux eux-mêmes qu’on peut être amenés à les modéliser par des poutres verticales avec ressorts (méthode 1). On peut également utiliser des logiciels spécifiques.
Dans tous les cas, il ne faut pas oublier d’intégrer dans les coefficients Kx ou Ky l’ensemble des exigences réglementaires comme l’effet de groupe.
Enfin, dans le cas où les pieux sont calculés par une autre entité que celle en charge du modèle de la superstructure, des itérations peuvent être nécessaires pour arriver à une convergence des efforts.
Exemple de calcul d'une matrice de raideur.
Données : pieux de diamètre 1.20 m, Ebéton= 30000 MPa, Ksol= 6495 (kN/m)/m, hauteur de semelle 2.00 m.
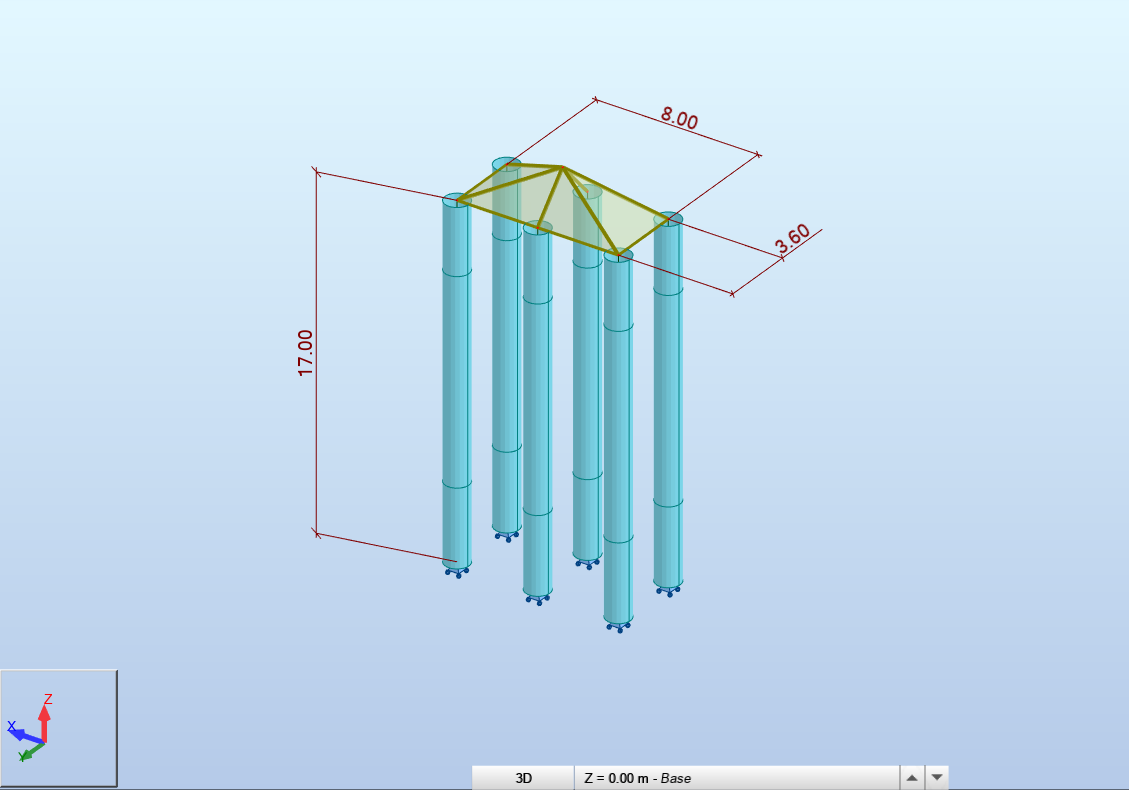
Géométrie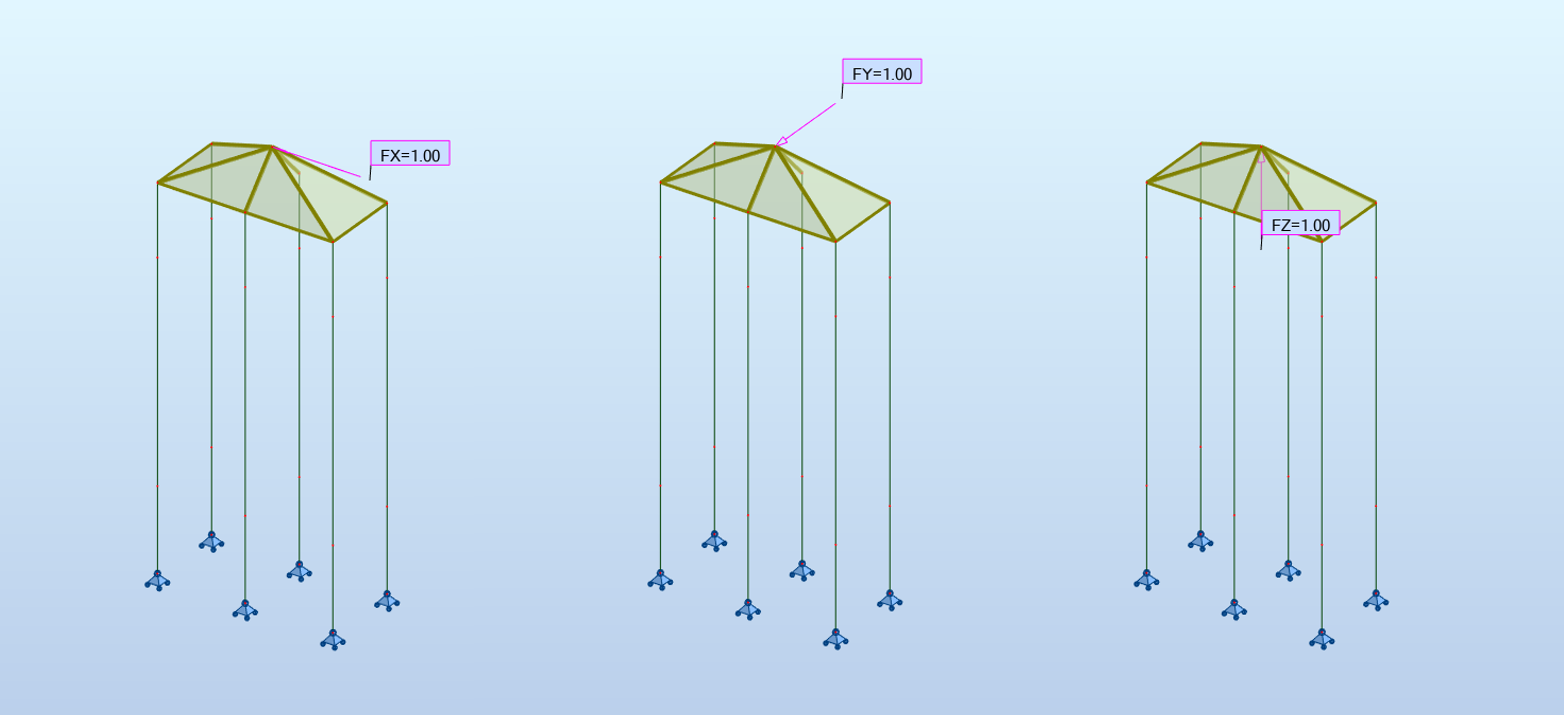
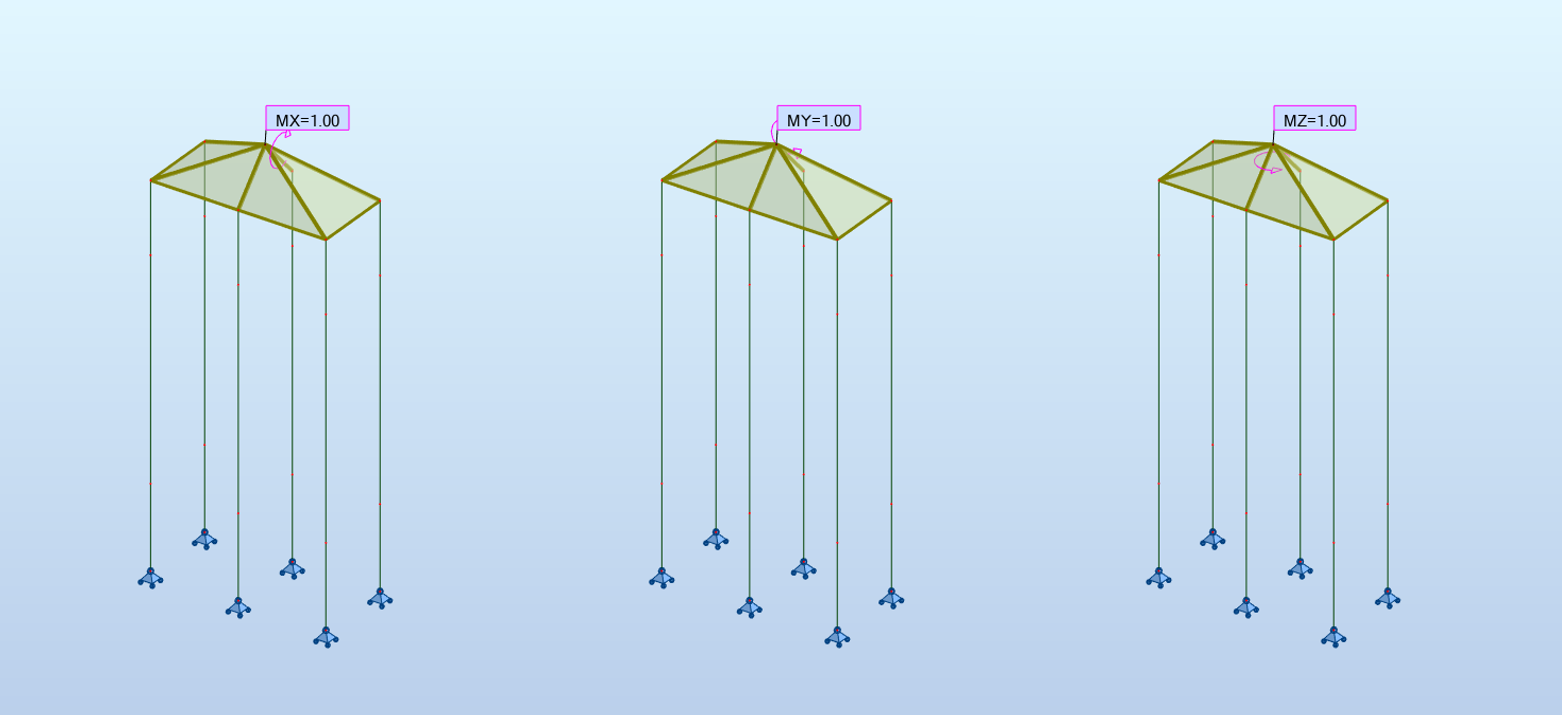
Efforts unitaires (1 kN ou 1 kN.m) introduits
Résultats:
Déplacements sous ces efforts = la matrice de souplesse [S]

Matrice de raideur [K]=[S]-1 - (unités : KN, KN.m, m et rad)
(Les matrices s'inversent très simplement à l'aide d'un tableur).
Incidence de la non prise en compte des termes croisés : on ajoute une pile de hauteur 10 m et de section 5.00×1.00 m², E=32000 MPa au modèle précédent. La même pile est modélisée avec un encastrement élastique à 6 composantes qui sont les termes de la diagonale de la matrice ci-dessus. On applique un effort de 1000 kN longitudinal (respectivement transversal) en tête: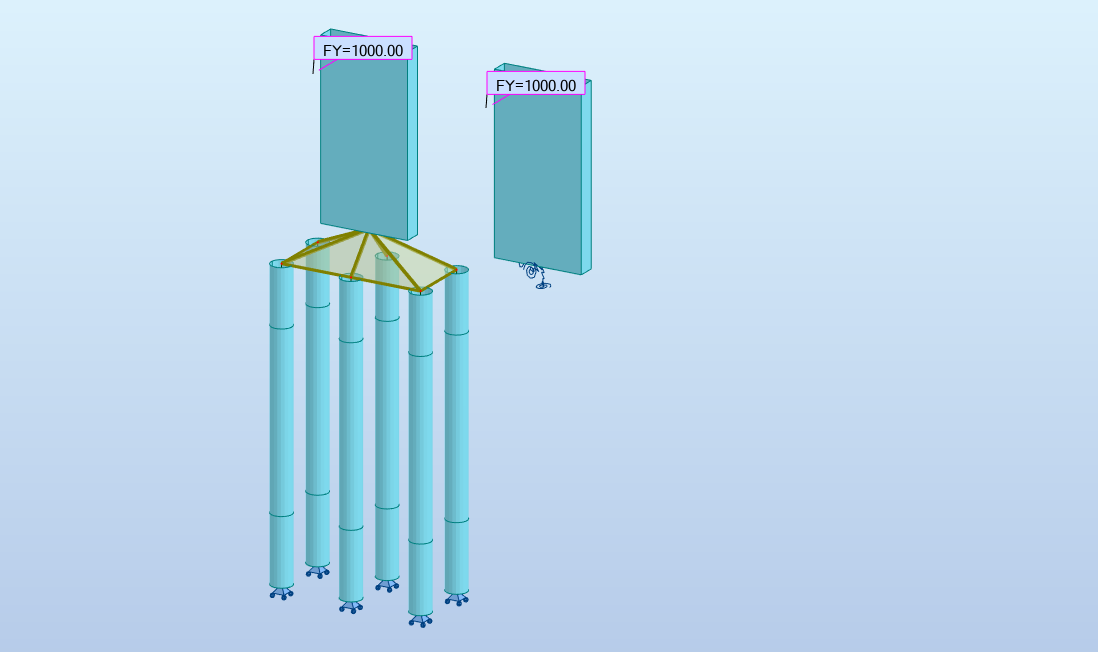
Dans ce cas de figure, on obtient un écart de l'ordre de 13% sur le déplacement longitudinal (respectivement 17% sur le déplacement transversal) - la souplesse de la pile intervient mais elle est identique dans les deux cas. Il appartient à l'ingénieur de juger de l'incidence de cette simplification éventuelle.
Une des sujets qui doit être traité dans la note d'hypothèse générales est relative aux simplifications que l'on va accepter ou non pour le calcul d'ISS. Elle sont liées à la prise en compte, d'une part, des modules à court et long terme du sol (ratio de 2 sur K) et du béton constitutif de la structure (ratio de 3 sur E) et, d'autre part, aux lois de comportements introduites pour le sol (linéaires, à plusieurs pentes, avec un palier de plastification possible). Suivant le logiciel utilisé, vouloir intégrer tous ces facteurs peut s'avérer très complexe, conduire à monter plusieurs modèles différenciés et à effectuer certaines vérifications manuellement (remplacement de ressorts plastifiés par un effort équivalent, par exemple). Effectuer un calcul en fourchette peut s'avérer intéressant dans certains cas, en distinguant les vérifications de résistance de celles de déformations.
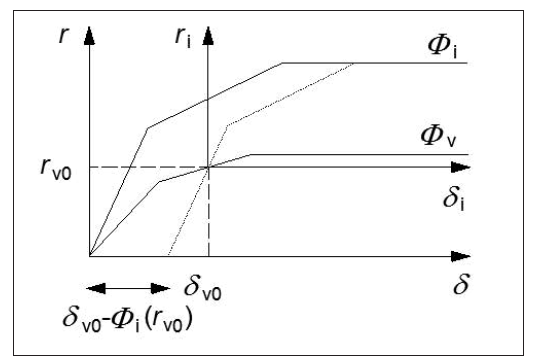
Illustration de la complexité de la loi de comportement des ressorts de sol
C.5.3 Modélisation des appareils d’appui

Les appareils d’appui d’une structure peuvent être modélisés de deux manières :
-
soit sous forme d’un appui, avec les degrés de liberté et paramètres de souplesse de l’appareil. Dans ce cas on récupère des réactions d’appui ;
-
soit sous forme d’un élément barre avec plusieurs possibilités de modélisation (décrites ci-après).
Dans tous les cas, les appareils d’appui doivent être placés à la position réelle (excentrement transversal et vertical) sous peine de grosses erreurs.
Il est à noter que le comportement des appareils d’appui peut être une source de non-linéarité (appareils d'appui glissants, par exemple) et nécessiter de facto un calcul non-linéaire.
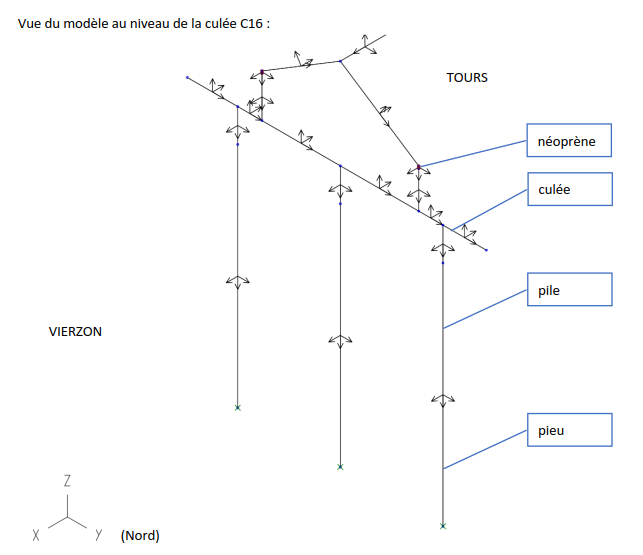
Exemple d’une modélisation d’une pile de pont incluant les appareils d'appui en élastomère fretté.
Si on recourt à des éléments barres, il y a plusieurs choix possibles :
-
certains logiciels proposent des éléments de type pièces de liaison qui reproduisent les caractéristiques des appareils d’appui (il ne s'agit donc pas à proprement parler d'une barre) ;
-
on peut également utiliser des éléments “ressorts” entre deux barres, si le logiciel le permet ;
-
on peut définir une « poutre de cisaillement », c’est-à-dire une barre très rigide en flexion mais ayant une déformabilité calibrée à l’effort tranchant. Il faut forcément que le logiciel prenne en compte la déformation d’effort tranchant (option non activée par défaut dans certains logiciels). On définira alors, pour cette barre, une section non pesante, une inertie et une section droite fortes, et bien sûr une section réduite à l’effort tranchant permettant de retrouver une équivalence de l’appareil d'appui (pour la barre GS/h ⇔ G'S'/T pour l'appareil d'appui ) ;
-
on peut enfin utiliser une barre classique, fonctionnant en flexion, encastrée en pied et libre en tête. On définira alors, pour cette barre, une section non pesante, une section réduite à l’effort tranchant forte et une inertie calibrée pour avoir une déformation globale équivalente à celle de l’appareil (pour la barre 3EI/h3 ⇔ G'S'/T pour l'appareil d'appui ).
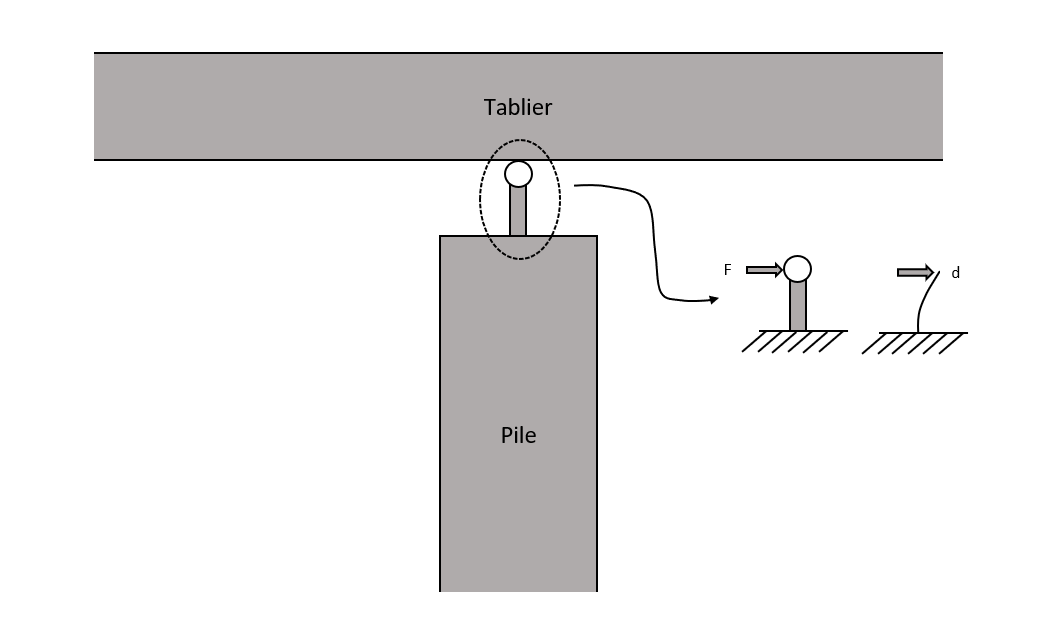
Quelle que soit la méthode, il faut que l’élément ait un comportement global équivalent aux caractéristiques des appareils d’appui, telles que définies par les normes des appareils d'appuis (série NF EN 1337) et il ne doit pas introduire de moment ni dans le tablier, ni dans la pile (autre que celui lié à l'épaisseur de l'appareil). .
L'illustration ci-dessous montre des extension rigides permettant de modéliser une tête de pile supportant deux travées isostatiques, simplement reliées par une dallette.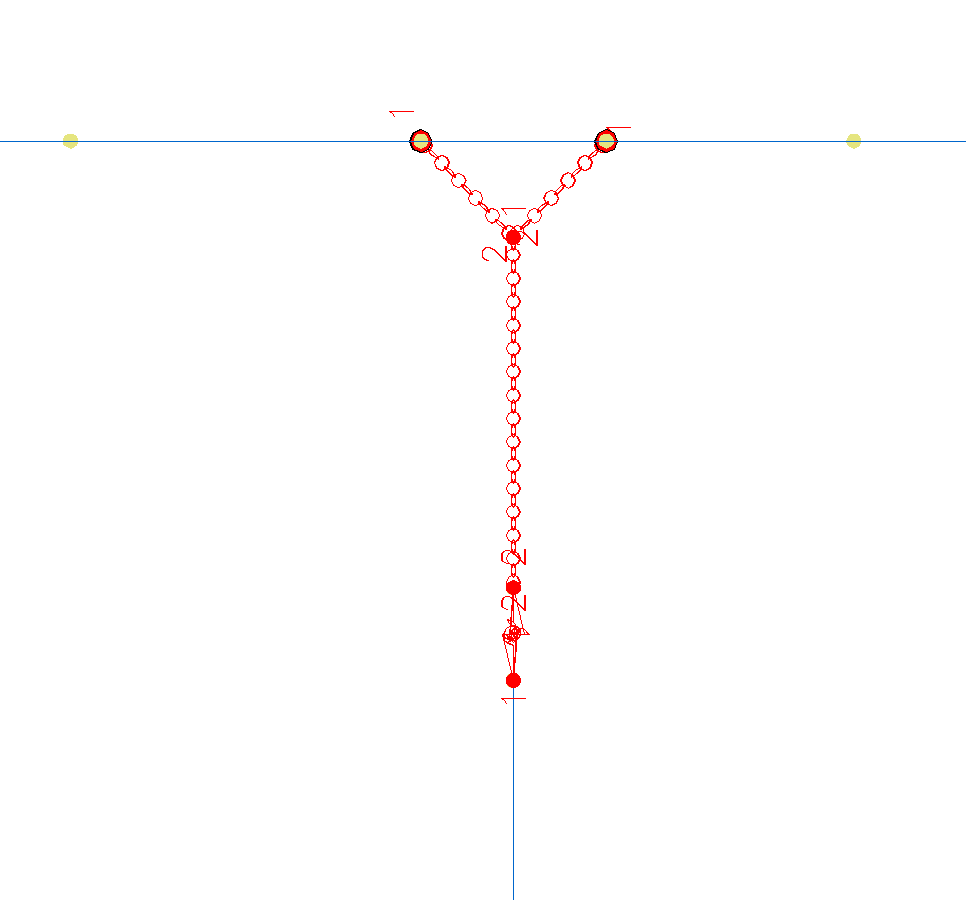
Détail de modélisation d’une pile supportant deux travées isostatiques
C.6 Connexions – liaisons – assemblage
C.6 Connexions – liaisons – assemblage
C.6.1 Relâchement des barres / ressorts / degrés de liberté
Dans tous les modèles, la connexion par défaut entre deux éléments poutre est un encastrement parfait. Il faut pourtant pouvoir libérer des degrés de liberté sur certains nœuds de connexion entre éléments (poutre-poteau, plaque de glissement). Chaque logiciel a des fonctionnalités différentes sur ce point.
Il est important de s’appuyer sur la notice du logiciel et surtout de vérifier, avec des cas de charge simples et avec les déformées statiques ou modales, que le comportement de la connexion est conforme à ce que l’on recherche.
C.6.2 Continuité de maillage
Il arrive qu’au niveau de la ligne ou de la surface de raccord, le nombre d’éléments ne soit pas le même de part et d’autre de la ligne (ou de la surface). Le risque est alors que seuls les nœuds communs (en vert) soient pris en compte comme connexion. (figure ci-dessous).
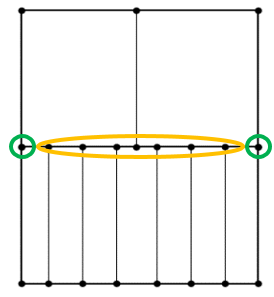
Mauvais raccord d’éléments finis de même type et ddl
Plus communément, on peut aussi créer une zone de transition en utilisant des éléments ayant les mêmes ddl par nœud mais de forme géométrique adaptée (figure ci-dessous).
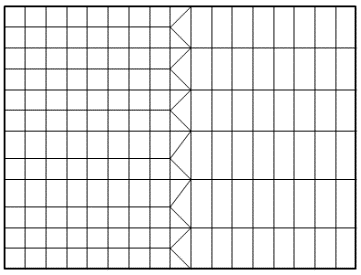
Maillage de la zone de transition
C.6.3 Connexion d’éléments de différentes natures
Le fait d’utiliser dans un même modèle des éléments de nature différente introduit de la complexité et il convient toujours de s’interroger sur l’utilité réelle de mélanger les éléments. La complexité est localisée au droit des liaisons entre des éléments de différentes natures. Ces liaisons peuvent être une liaison poutre/coque, une liaison coque/volume ou une liaison poutre/volume.
On veillera particulièrement à la liaison éventuelle de types d’éléments structuraux différents : élément à 6 degrés de liberté (UX, UY, UZ, ROTX, ROTY, ROTZ) / élément à 3 degrés de liberté (UX, UY, UZ). Ce type de liaison peut occasionner l’apparition d’instabilités ou de rotules non attendues.
Un certain nombre de logiciels compensent ces difficultés avec des éléments spécifiques capables de traiter ces liaisons et les problèmes de degré de liberté. Il convient de s’en assurer et de vérifier la pertinence du comportement local du modèle.
C.6.4 Connexion entre une barre et une plaque
Trois cas se présentent :
-
soit les éléments poutre et plaque sont dans le même plan ;
-
soit la poutre constitue une nervure de la plaque ;
-
soit la poutre et la plaque sont perpendiculaires.
C.6.4.1 Barre et plaque coplanaires
Ainsi pour un élément barre relié à deux éléments de plaques, il convient que le transfert des moments soit assuré par l’intermédiaire d’éléments supplémentaires, ou par l’introduction d’équations de contraintes liant les degrés de liberté.
Dans les illustrations ci‐dessous, dans le cas 1, il risque de ne pas y avoir un transfert correct de moment et rien n’oblige la barre à rester perpendiculaire à la plaque (intrinsèquement les nœuds des coques ne peuvent pas bloquer de moment d'axe perpendiculaire au plan des EF). Le cas 2 consiste à imposer une équation qui lie les déplacements du bord de la plaque avec la barre. C’est une méthode fiable mais qui n’est pas proposée par tous les logiciels. Les cas 3 et 4 consistent à ajouter des barres rigides pour reproduire l’asservissement en déplacement. Il faut notamment prêter attention à la définition de la rigidité de ces barres qui peut être source d’instabilité du logiciel.
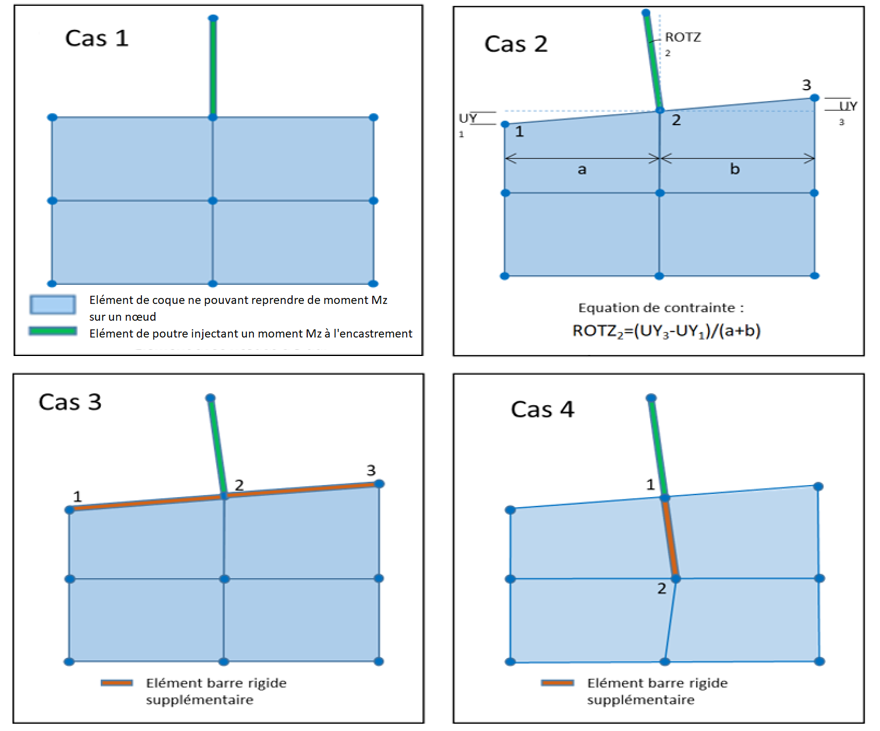
Liaison d'éléments de nature différente - Transfert de moment
C.6.4.2 Connexion entre une barre et une plaque hors plan
Le cas où la poutre joue le rôle d’un raidisseur associé à la plaque comme pour les dalles nervurées est traité de manière détaillée en C.8 Sections composées (poutres/dalles).
C.6.4.3 Connexion d’une barre perpendiculaire à une plaque
Le dernier cas est celui de la connexion poteau-plaque. La grosse difficulté, en plus de la transmission de la flexion de la barre à la plaque, est la transmission de la torsion de la barre à la plaque. Par défaut, la plaque n’ayant pas de dll de rotation autour de l’axe perpendiculaire à son plan, elle ne peut pas reprendre de moment de torsion amené par le poteau. Il faut donc retrouver les bonnes conditions de liaison cinématique. Pour assurer la reprise des efforts de flexion et de torsion de la barre par la plaque, il est nécessaire de disposer des liaisons rigides à la jonction (en rouge sur les schémas ci-dessous)
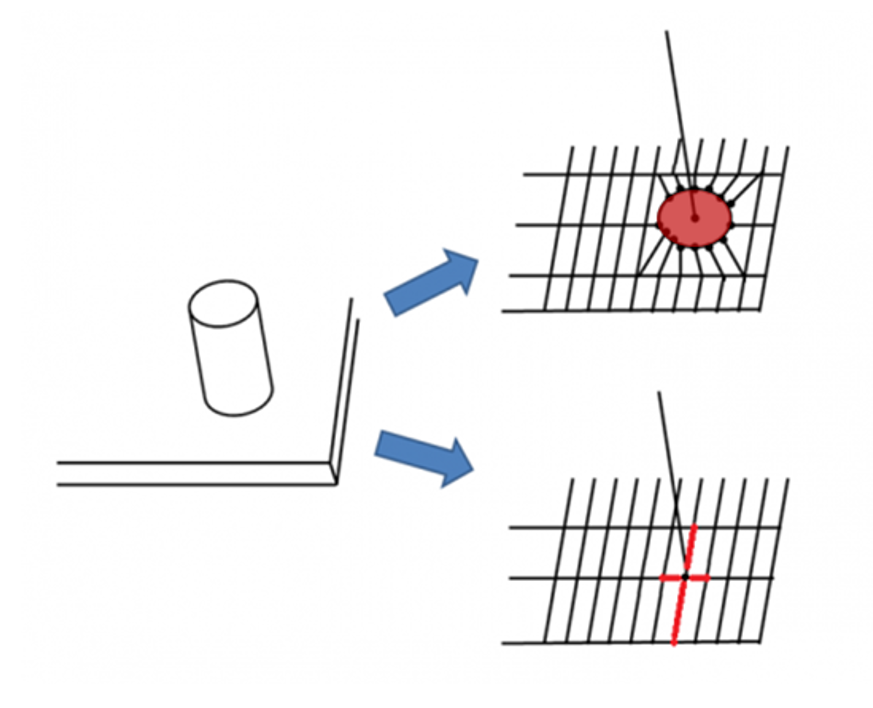
Modélisation du raccord barre-plaque (tablier supporté par un poteau, vu par le dessous)
Exemple du poteau (élément filaire) encastré dans une plaque et soumis à de la torsion.
Illustration de la prise en compte du nombre de degrés de liberté différents entre éléments de nature différente.
On modélise une plaque de 20 cm d’épaisseur en béton sur laquelle est « encastré » un poteau en béton de 1 m de diamètre, en reliant simplement l’about inférieur du poteau à un nœud de la plaque :

Les translations horizontales sont bloquées aux coins de la plaque de manière à bloquer cette torsion. Le couple introduit vaut 10 MN.m.
Résultats :
Le calcul informatique converge, malheureusement, mais … plusieurs points peuvent et doivent attirer l’attention du modélisateur dans les résultats :
-
la valeur de la rotation, à la fois en tête et en pied de poteaux (54.2 radians!) ;

-
la présence de moments Mz dans les angles alors que les appuis sont relâchés en Rz ;
-
la somme des réactions n’est pas nulle ;
-
enfin, la valeur des réactions Fx et Fy paraît faible (ordre de grandeur à trouver 10000 kN.m/7 m (bras de levier)/4 points= 360 kN).
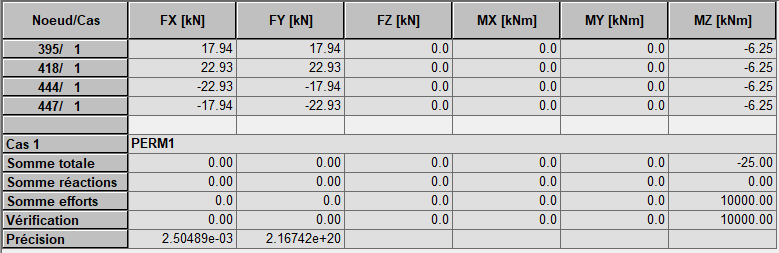
Il suffit de créer un encastrement à l'aide de barres (fictives) en pied de poteau, dans la dalle …
… pour obtenir des résultats globaux justes. (Les efforts locaux en pied de poteau sont bien sûr perturbés par ces barres fictives).
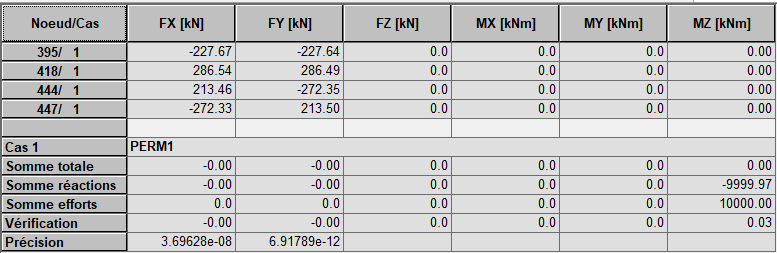
C.6.5 Connexions plaque/volume et poutre/volume
Dans le cas d’un raccord Plaque-Volume, il est nécessaire de mettre en place une liaison permettant d’équilibrer le moment d’encastrement. Comme en C.6.4, on peut soit créer une plaque de liaison à la surface du volume (d’un seul côté ou des 2 côtés) , soit prolonger la coque à l’intérieur du volume.
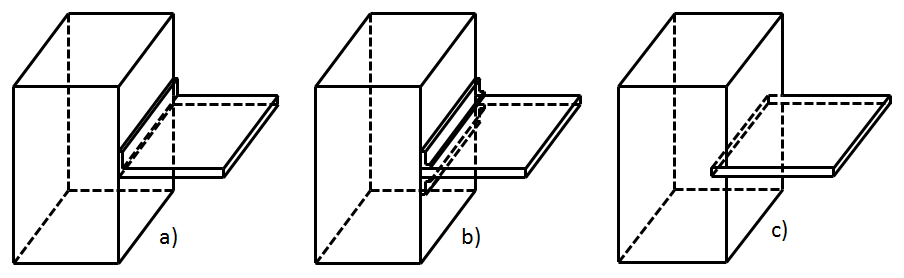
Modélisation du raccord Coque-Volume
On applique le même raisonnement dans le cas d’un raccord Poutre-Volume.
C.6.6 Valeurs de rigidité / écarts de rigidité / « infiniment rigide »
De nombreux logiciels proposent un élément « barre rigide » ou « liaison rigide ».
Cet élément est tantôt un asservissement cinématique (relation mathématique) entre deux éléments et tantôt une barre fictive dont la rigidité est très grande.
Or la présence, dans la matrice globale du système, d’éléments avec de grands écarts de rigidité peut poser des problèmes de convergence. Voir l’exemple final sur le calcul matriciel présenté au paragraphe A.1 .
Ces instabilités ou erreurs numériques n’apparaissent pas forcément avec un message d’erreur.
Dans la plupart des cas, il est conseillé d’utiliser des éléments dont on définit soi-même la raideur et de tester l’influence de cette raideur sur le comportement global.
C.6.7 Liaisons d'éléments de natures différentes : Zoom structurel - Exemples
-
Insertion d'éléments finis de type plaques dans un modèle global
Pour appréhender le comportement spécifique d'une zone particulière d'un ouvrage modélisé à l'aide d'éléments filaires, et pour ne pas avoir à gérer un modèle trop lourd, on peut être amené à y insérer des éléments plaques, en lieu et place des éléments filaires initiaux. La liaison entre ces deux parties de nature différente se fait via des liaisons ou barres rigides en “toiles d'araignées”.
Exemples de liaisons d'un modèle filaire global avec des parties modélisées en plaques :
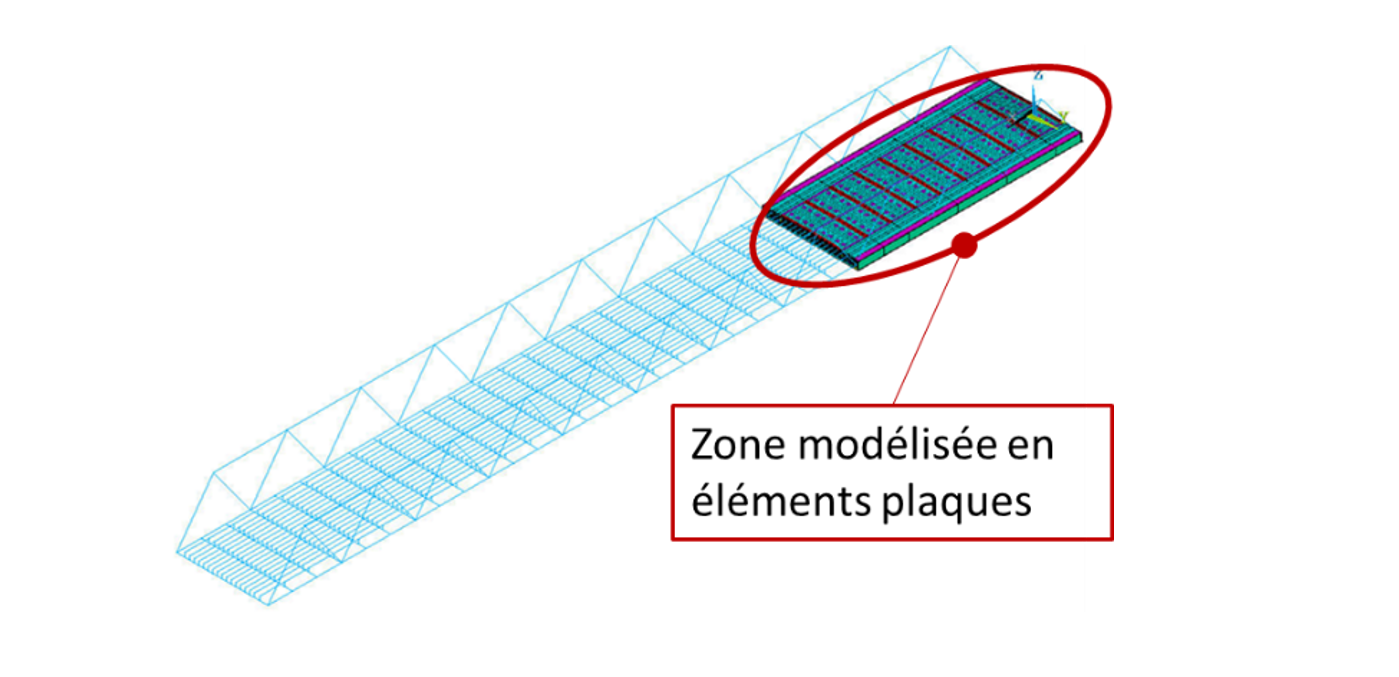
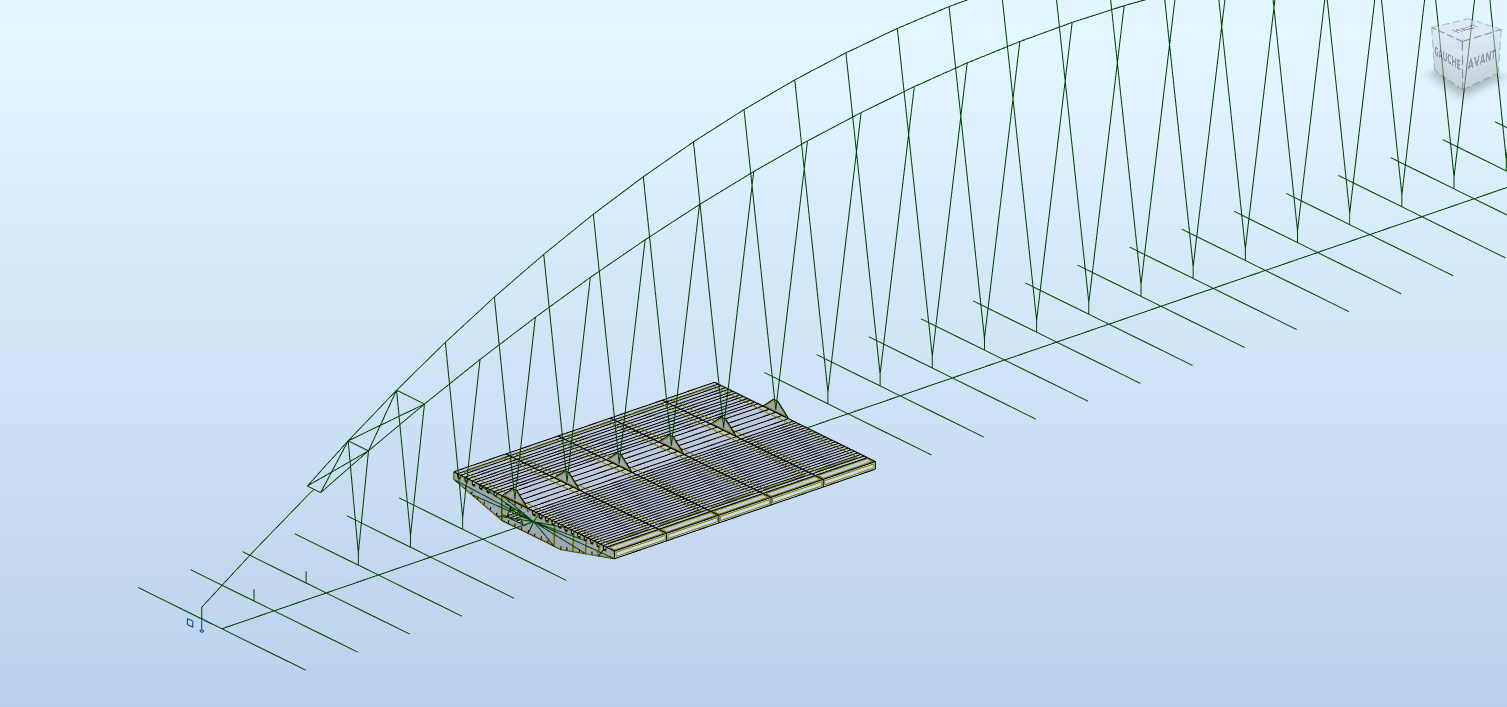
-
Zoom structurel
On peut aussi souhaiter modéliser uniquement une partie de l’ouvrage en éléments plaques et venir placer aux frontières de cette partie les déplacements ou les efforts aux nœuds issus du modèle global filaire (principe du zoom structurel). Ces déplacements ou ces efforts sont alors transmis aux éléments de plaques par l’intermédiaire de liaisons rigides constituées d’éléments de type poutres. Ces zones de liaisons entre poutres et plaques doivent être modélisées suffisamment loin de la zone à étudier pour s’assurer que les efforts introduits par les liaisons rigides soient diffusés correctement jusqu’à la zone d’étude.
Par exemple, dans le cadre de l’analyse d’une zone de raccordement de deux PRS (Poutres Reconstituées Soudées), la zone a été modélisée en éléments plaques et coques (voir figure ci-après). Aux extrémités des PRS modélisés sur une certaine longueur, on introduit des torseurs par l’intermédiaire de liaisons rigides, la structure étant appuyée au niveau de la platine inférieure. La vue ci-après montre que ces liaisons rigides sont situées suffisamment loin (à près de 2 m) de la zone à étudier. Il est à noter que la platine est suffisamment rigide pour ne pas avoir à créer de liaisons rigides.
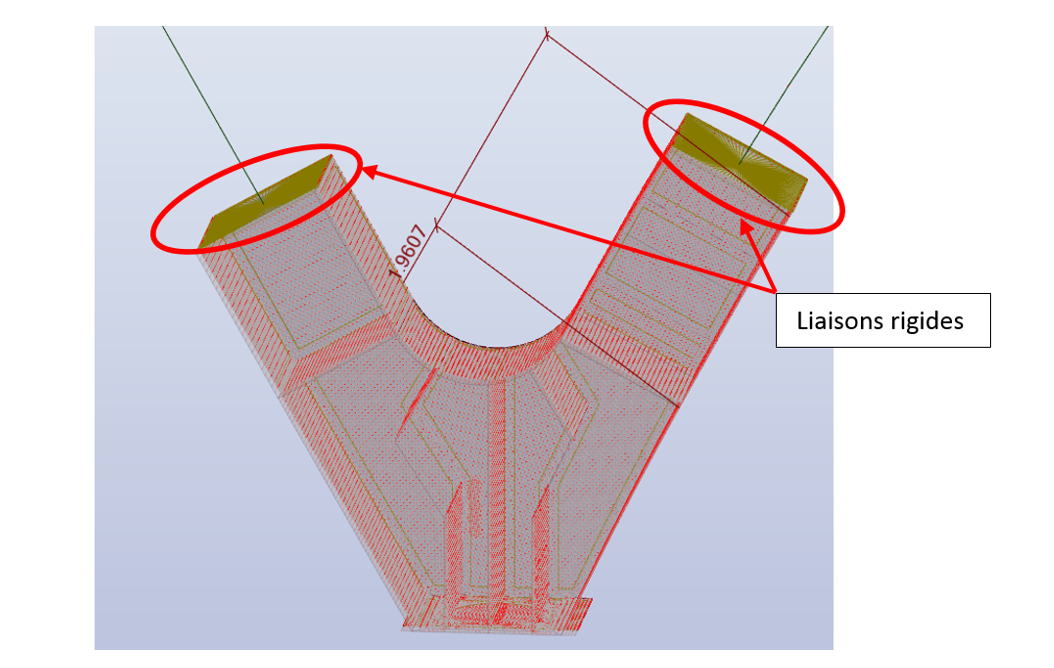
L'exemple ci-après représente la structure singulière du caisson d'about d'un ouvrage d'art relativement large. Les deux réactions d'appuis sont introduites (à droite) sous ce caisson qui est réputé parfaitement encastré dans le tablier (à gauche). Elles sont issues d'un modèle filaire/plaques global. Le poids propre et les charges sur le caisson en lui-même sont modélisées, le cas échéant. Cette approche simplifie l'introduction des données, puisqu'elle ne nécessite que quelques réactions d'appui plutôt que des torseurs complexes à obtenir à la coupure avec le tablier de par la nature du modèle global.

Modèle global avec modélisation simplifiée du caisson d'about.

Modèle local détaillé du caisson d'about
C.7 Excentrements
C.7 Excentrements
La plupart des logiciels aux éléments finis proposent des options permettant de définir une poutre sur une fibre autre que sa fibre neutre.
Cette option est très utile, notamment :
-
pour créer facilement des liaisons entre éléments de hauteurs (ou d'épaisseurs) différentes ou variables, mais qui ont une face alignée (voir ci-dessous);
-
pour définir la géométrie d'un tablier de hauteur variable (il est plus simple d'introduire une géométrie d'extrados figée et de gérer par ailleurs un décalage vertical extrados/CDG susceptible de varier, lui, pendant la conception) ;
-
pour l’application des charges sur une face (par exemple sur l’extrados d’un pont, pour la création de “routes” de chargement).
Il convient par contre de définir le décalage entre cette fibre de définition et la fibre neutre, ce décalage étant l’excentrement qui peut varier le long de la barre.
En cas de doute sur le fonctionnement de cette option, on pourra vérifier le bon fonctionnement avec un autre modèle où chaque poutre est définie à sa fibre neutre en créant soi-même l’excentrement avec des liaisons rigides.
Le sujet des excentrements est partiellement illustré dans le document Exemple de précontrainte et excentrement.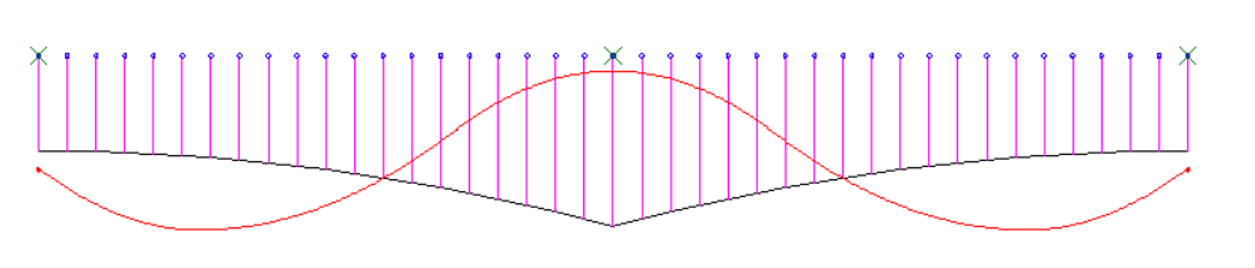
Illustration de l'excentrement d'une série de barres par rapport à un extrados horizontal
$translationBooksC.8 Sections composées (poutres/dalles)
C.8 Sections composées (poutres/dalles)
Les sections composées sont constituées par l’assemblage, rigide ou élastique, d’éléments de nature différente (bois, acier, béton, …) et/ou à des dates différentes.
Nous étudions ici les cas les plus courants rencontrés dans les modélisations :
-
planchers de bâtiments (dalles+poutres) ;
-
poutres d'ouvrages d'art (type PRAD) ;
-
poutres de ponts mixtes acier/béton ;
-
planchers mixtes de bâtiment (profilés métal + dalle BA).
Ces éléments complexifient le calcul avec des approches très différentes selon le cas étudié.
C.8.1 Poutre plancher de bâtiments
Ce chapitre concerne les planchers de bâtiments calculés à partir d'une modélisation globale du bâtiment.
C.8.1.1 Principe du calcul
La difficulté sur ce type d'analyse est de concilier les calculs aux éléments finis avec les règlements de calcul du béton armé.
En effet, les règlements de béton armé (BAEL et EC2-1-1 §5.3.2.1) sont fondés sur des règles précises sur les largeurs participantes, sur le décalage des courbes de moment (qui correspondent à la formation des bielles) et sur le diagramme de déformations des sections (cohérences entre les déformations de la dalle et de la poutre).
Or les modèles éléments finis sont fondés sur la RdM et pas sur ces règlements.
Dans tous les cas, le calcul du ferraillage doit être fait :
-
en tenant compte du sens de portée de la dalle (notamment des éléments préfabriqués) ;
-
en récupérant des efforts du modèle ;
-
en les corrigeant pour tenir compte des largeurs participantes (les bandes non participantes pèsent mais ne portent pas) ;
-
en les corrigeant pour tenir compte des excentrements additionnels non modélisés (verticaux ou horizontaux - effet P-Δ) ;
-
en les corrigeant du décalage des moments ;
-
en refaisant un calcul réglementaire avec ces efforts post-traités.
C.8.1.2 Comment modéliser le plancher poutre/dalle
Le premier point concerne la méthode de modélisation du plancher, en effet plusieurs options se présentent :
-
ne modéliser que les poutres, les charges étant directement appliquées aux poutres ;
-
modéliser les poutres et les dalles sur la même fibre moyenne ;
-
modéliser les poutres excentrées par rapport aux dalles.
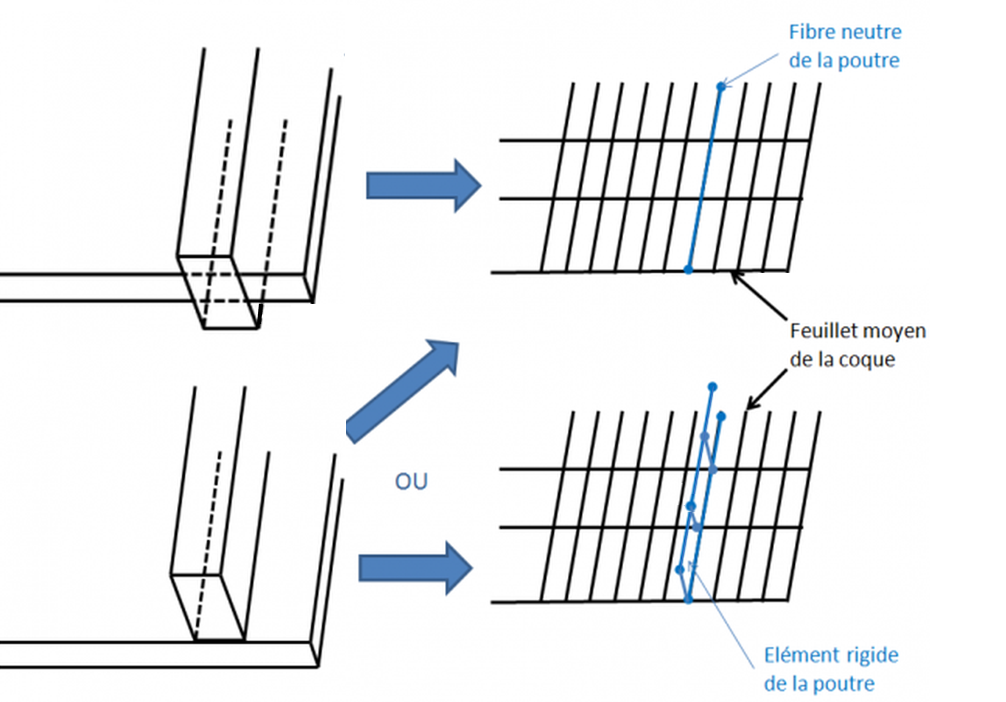
Illustration des deux dernières approches
La comparaison entre ces cas est réalisée à partir de l'exemple suivant :
Soit une structure à 2 travées de 8 m chacune, les poutres 25 cm x 50 cm ht sont espacées de 2 m, la dalle a une épaisseur de 15 cm.
Vue en plan de la dalle
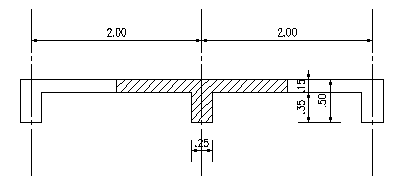
Coupe transversale
On étudiera la poutre centrale :
Chargement = poids propre + charge permanente additionnelle (revêtement) de 3 kN/m2 + surcharges de 5 kN/m2.
Nous étudions le cas ELU (1.35 CP + 1.5 Q).
Il y a 3 types de modélisation :
-
Cas 1 : la dalle n’est pas modélisée, ce qui revient à calculer la poutre selon les méthodes usuelles du béton armé ;
-
Cas 2 : la dalle est modélisée sur la même fibre moyenne que celle de la poutre ;
-
Cas 3 : la dalle est modélisée excentrée par rapport à la poutre.
Etude du cas 1 : modélisation de la poutre seule - la dalle n’est pas modélisée
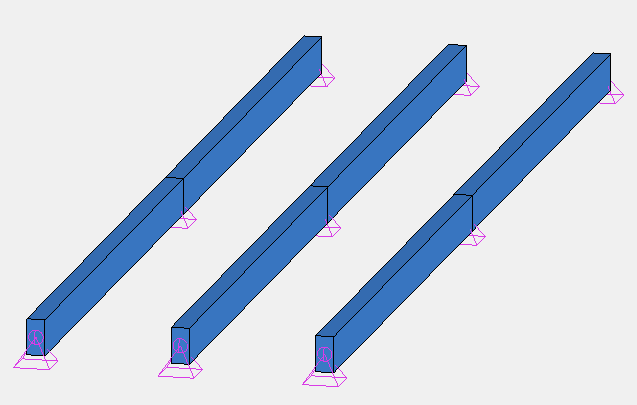
Schéma de la modélisation
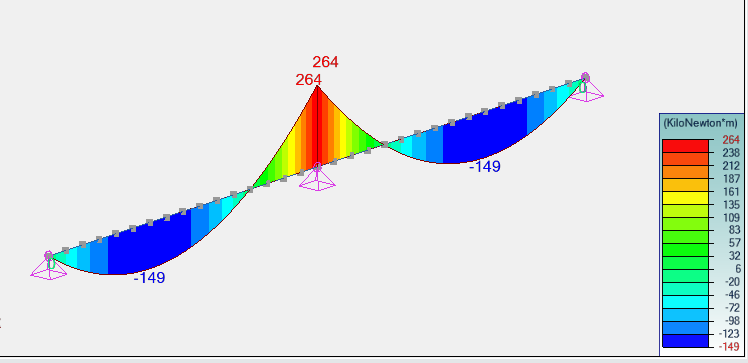
Courbe des moments fléchissants (kN.m) poutre
Les moments fléchissants sont égaux à -264 kN.m sur appuis et 149 kN.m en travée ; ils sont cohérents avec les méthodes classiques de calcul, cela nécessite un ferraillage de 19 cm² sur appuis et de 10 cm² en travée
Etude du cas 2 : la dalle et la poutre sont modélisées sur la même fibre moyenne
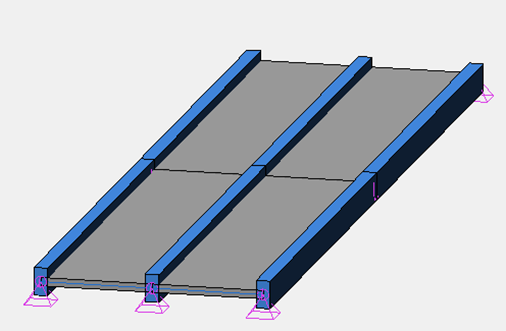
Schéma de la modélisation
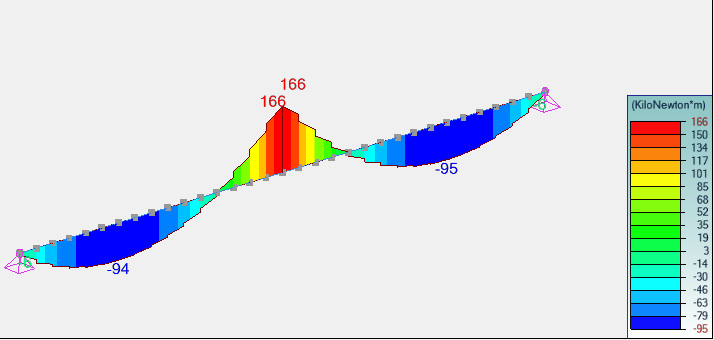
Courbe des moments fléchissants (KN.m) poutre
Les moments fléchissants dans la poutre sont égaux à -166 kN.m sur appuis et 94 kN.m en travée ; ces efforts sont beaucoup plus faibles (-37% !!) que ceux calculés dans le Cas 1 : le ferraillage calculé n’est plus que de 11 cm² sur appuis et 6 cm² en travée.
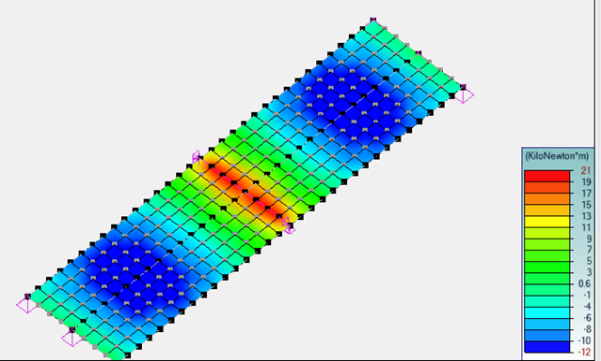
Moments longitudinaux dans la dalle
Les moments fléchissants dans la dalle sont égaux à -21 kN.m/ml sur appuis et 12 kN.m/ml en travée, ce qui se traduit par un ferraillage sur appui As = 5 cm²/ml, Ai = 0 et en travée As = 0, Ai = 3 cm²/ml
Etude du cas 3 : la poutre est excentrée par rapport à la dalle
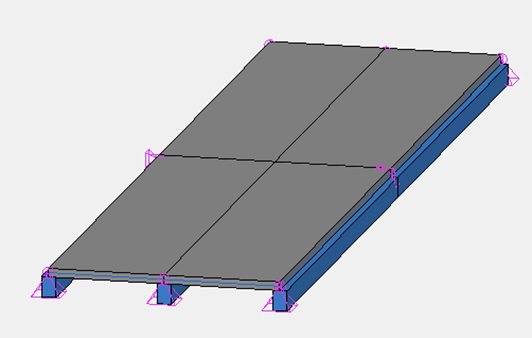
Schéma de la modélisation
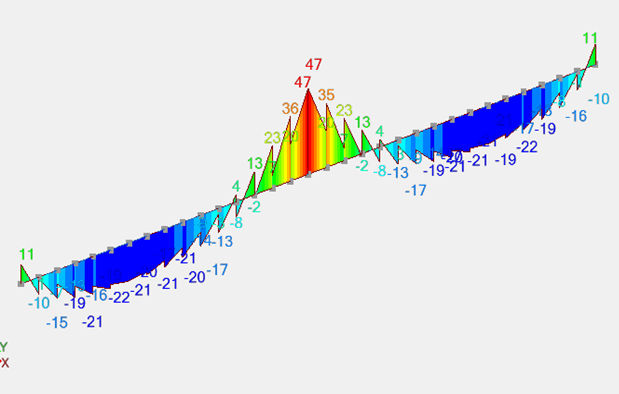
Courbe des moments fléchissants (kN.m) poutre
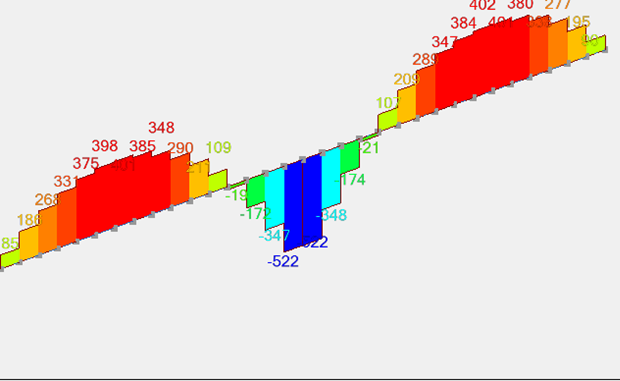
Courbe des efforts normaux (kN) dans la poutre
Les moments fléchissants dans la poutre sont égaux à -47 kN.m sur appuis et 21 kN.m en travée, mais ils sont accompagnés d’efforts normaux (traction sur appuis et compression en travée) ; le ferraillage calculé est alors de 10 cm² en nappe supérieure et 2 cm² en nappe inférieure sur appuis, tandis qu'il n'y a pas d’aciers en travée !!!
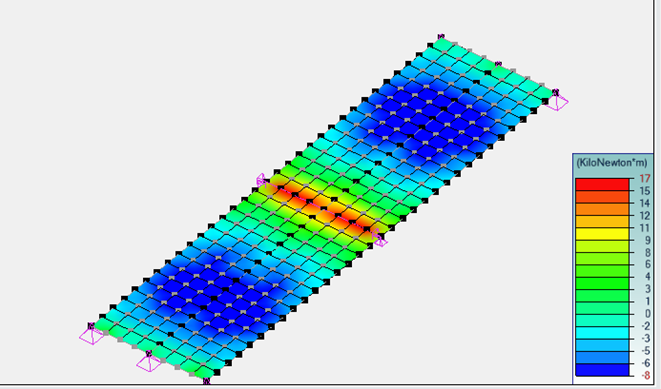
Moments longitudinaux dans la dalle
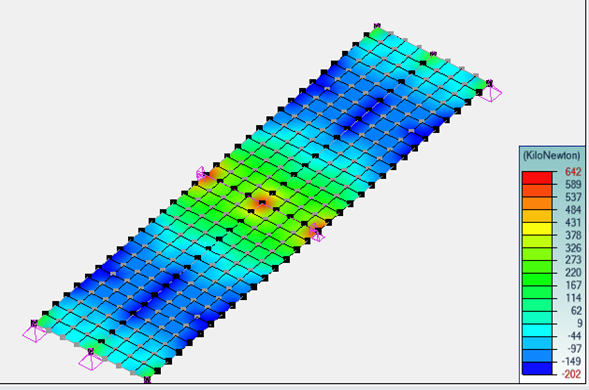
Efforts normaux longitudinaux
Les moments fléchissants dans la dalle sont égaux à -17 kN.m/ml sur appuis et 9 kN.m/ml en travée, ils sont accompagnés d’efforts normaux avec pics sur appuis.
L’analyse montre que le cas 3 avec la prise en compte des excentrements est inexploitable et incompatible avec les calculs réglementaires, car il apparaît des efforts normaux et des pics d’efforts dans la dalle. En effet, comment prendre en compte le décalage des courbes des moments en tenant compte des efforts normaux ?
Les tableaux ci-après résument les principaux résultats.
| Appuis | Travée | ||
| CAS 1 | poutre | 19 cm2 | 10 cm2 |
| dalle | 0 cm2 /ml | 0 cm2 /ml | |
| total | 19 cm2 | 10 cm2 | |
| CAS 2 | poutre | 11 cm2 | 6 cm2 |
| dalle | 5 cm2 /ml | 3 cm2 /ml | |
| total | 20 cm2 | 12 cm2 | |
| CAS 3 | poutre | 10 cm2 | 0 cm2 |
| dalle | inexploitable | inexploitable | |
| total |
Sections d’aciers sur appuis et en travée pour les 3 méthodes de calcul
Les cas 1 et 2 donnent des sections d’aciers proches, ce qui semble valider la modélisation de la poutre et la dalle sur la même fibre moyenne, mais il ne faut pas généraliser les conclusions de cet exemple car, comme le montrent les diagrammes de déformations des sections ci-dessous, il apparait une incohérence en travée avec des aciers tendus dans la dalle, situés au niveau de la zone comprimée de la poutre.
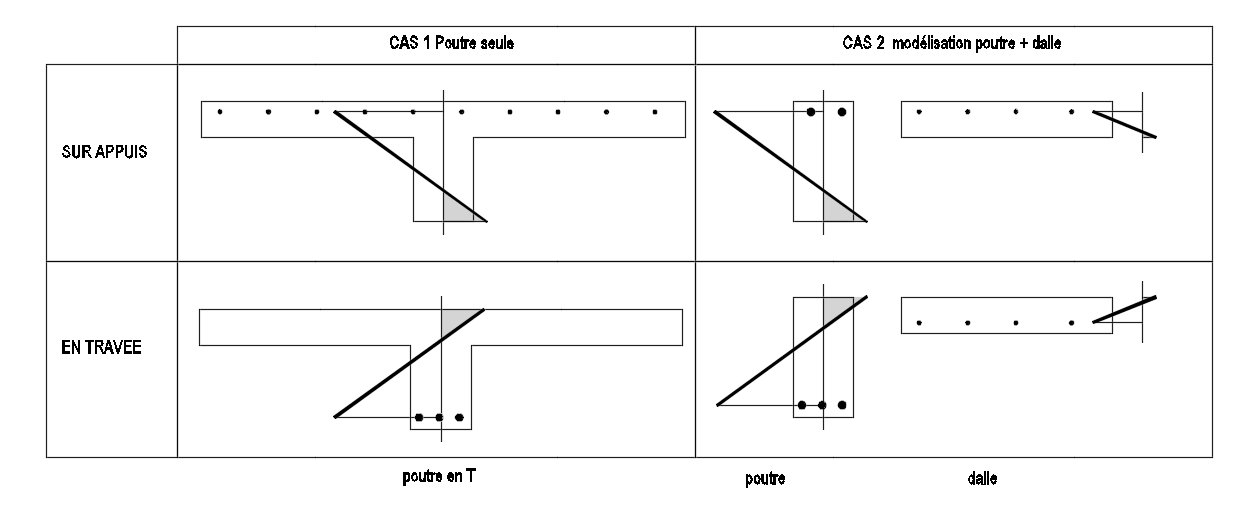
Cet exemple montre que :
-
ne modéliser que les poutres seules donne de bons résultats , mais cette option est difficilement applicable dans une modélisation globale (comment transmettre les efforts horizontaux par exemple ?) ;
-
modéliser un excentrement entre les poutres et les dalles permet une bonne modélisation de la raideur du plancher, mais ce n'est pas compatible avec les vérifications réglementaires (comment décaler la courbe de moments lors qu'une partie des moments apparait sous forme d'efforts normaux dans les poutres ?) ;
-
il ne faut pas calculer les ferraillages des poutres et dalles directement à partir des résultats de la modélisation générale.
C.8.1.3 Méthode générale de calcul d'un plancher poutre/dalle
Les calculs des dalles et des poutres doivent d'une part prendre en compte tous les efforts calculés dans la modélisation globale et d'autre part respecter les règles de calcul réglementaires.
Soit l’exemple d’un bâtiment soumis à des efforts horizontaux (vent, séisme, thermique, etc..) :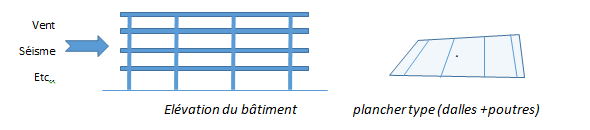
Etape 1 : Réaliser un modèle global du bâtiment. Cette modélisation globale permet de calculer les efforts dans les diaphragmes formés par les planchers, ce qui se traduit par l’apparition d’efforts de membranes (efforts normaux et cisaillements) dans les éléments horizontaux. Ce sont ces efforts que nous retiendrons pour la suite du calcul : Nxx,Nyy,Nxy dans les dalles et Nx dans les poutres.
Etape 2 : Réaliser un modèle local de la dalle. En effet, sauf cas très particulier, il n'est pas possible d'utiliser le modèle global d'un bâtiment pour justifier les dalles car, par exemple :
-
le phasage n'est généralement pas modélisé ;
-
les prédalles ne sont généralement pas modélisées ;
-
le positionnement des charges dans un modèle global ne respecte pas forcément les zones d'influence des poutres et dalles à l'échelle locale ;
-
du point de vue réglementaire, les poinçonnements, les redistributions d'efforts, les majorations forfaitaires des efforts, etc., ne sont pas pris en compte.
Dans le modèle local de la dalle, sa géométrie est extraite de la géométrie du modèle global. Dans un soucis de simplification, les poutres sont généralement remplacées par des appuis linéaires, tandis que les dalles sont modélisées par des éléments de coques (flexion) soumises aux chargements pondéraux. C'est ce modèle plan et de petite taille qui va être étudié de manière réglementaire en tenant compte éventuellement du phasage, des prédalles, etc..
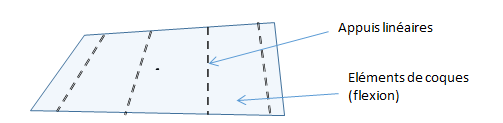
Les efforts de flexion (Mxx,Myy,Mxy) dans les dalles, résultants de ce modèle local doivent être cumulés aux efforts normaux (Nxx,Nyy,Nxy) de la modélisation globale pour calculer les ferraillages et procéder aux vérifications réglementaires (attention aux combinaisons).
Etape 3 : Réaliser un modèle local pour le calcul des poutres. En effet, pour des raisons identiques à celles évoquées pour les dalles, il n'est pas possible d'exploiter le modèle global pour déterminer l'intégralité des sollicitations dans les poutres.
La géométrie est identique à celle du modèle local de la dalle, si ce n’est que les poutres sont bien sûr conservées.
Dans ce modèle, les dalles ne doivent pas reprendre des efforts de flexion, elles doivent simplement jouer le rôle de transmission des charges sur les poutres, elles sont donc modélisées par des surfaces de répartition (se référer à la documentation du logiciel utilisé).
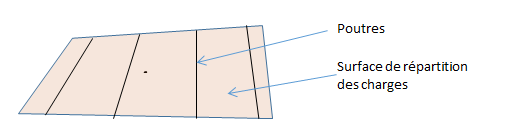
Les efforts résultants dans les poutres sont à cumuler aux efforts normaux de la modélisation générale, ce qui permet de procéder ensuite aux calculs réglementaires des poutres (soit manuellement, soit par logiciel dédié).
C.8.2 Cas des ouvrages d'art (dalles nervurées)
Cette approche s'applique aux ponts de type PRAD, VIPP, …
Pour le calcul des ouvrages d'art, si l'on omet la méthode de Guyon-Massonnet, la pratique consiste à calculer les structures:
-
en grillages de poutres, c'est à dire un croisement de barres longitudinales, représentant la section des nervures + le hourdis participant, et de barres transversales, modélisant le hourdis : l'avantage est que l'on a directement des torseurs exploitables en calcul de béton armé ou précontraint, l'inconvénient peut être le placement des charges, surtout les charges mobiles ;
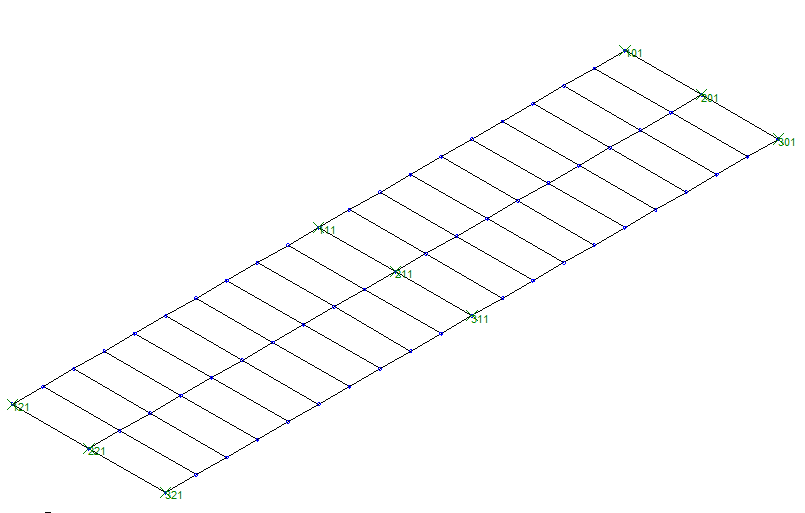
Modèle en grillage de poutres
-
en grillages de poutres utilisant des poutres échelles - peut être avantageux pour un calcul phasé, surtout si l'on veut modéliser finement des effets liés au fluage ou au retrait ;
-
comme dans la troisième approche ci-dessus (C.8.1.2), en modélisant les nervures via des barres et le hourdis excentré sous forme d'une coque EF : l'avantage réside dans le placement facilité des charges, l'inconvénient est que l'on n'obtient pas directement des torseurs exploitables en calcul de béton armé.
Il est à noter que les barres modélisant le hourdis doivent être perpendiculaires (ou quasi-perpendiculaires) entre elles pour que le modèle soit valide.
Pour illustrer cette approche, en particulier le ferraillage du hourdis et des nervures, nous repartons de l'exemple traité en C.8.1.
Vue du modèle – retombées 25 cm x 35 cm ht et hourdis de 15 cm d’épaisseur. Portées 2 x 8 m – entraxe des poutres 2 m.
Le calcul des armatures directement à partir d’un module de ferraillage n’est pas recommandé si l’on veut tenir compte des hypothèses en usage pour le calcul du béton armé. Un petit post processeur (un tableur) suffit à calculer le moment et la largeur de table affectée à la nervure, comme nous le verrons ci-après.
Application à la poutre centrale du modèle - section sur appui et section en travée (nota: les deux travées sont chargées par la charge d'exploitation en totalité, sans considération de ligne d'influence):
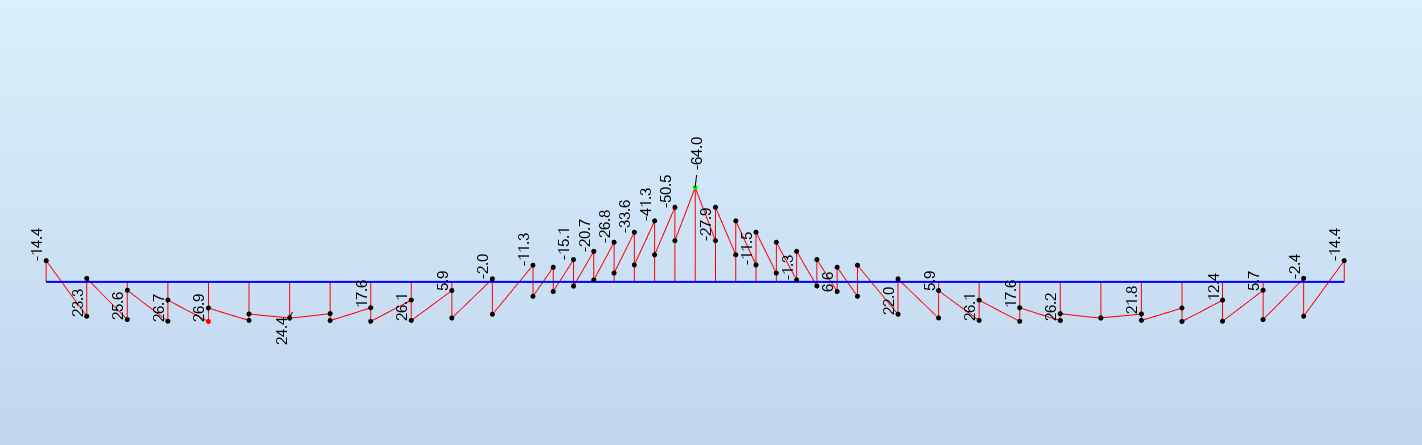
Moments de flexion (retombée seule) - kN.m
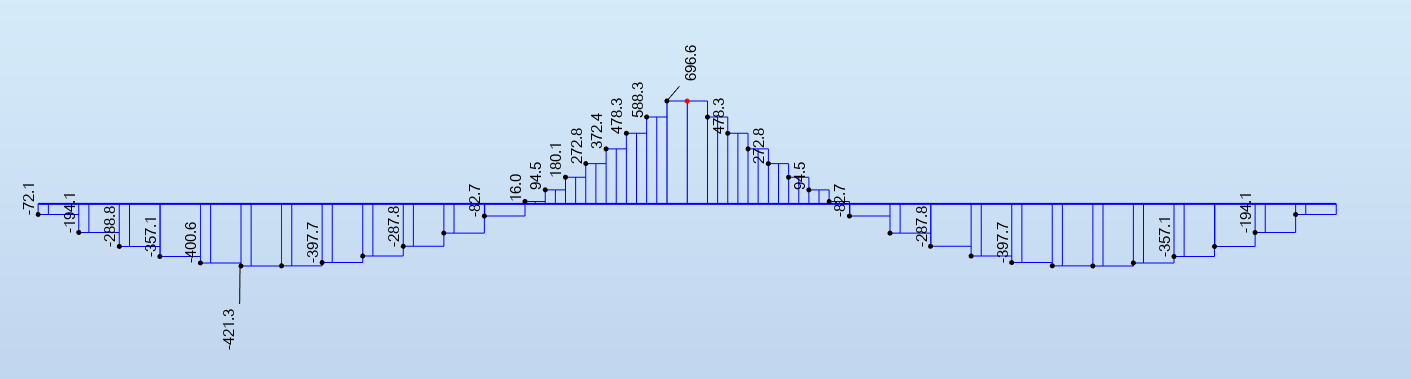
Effort normal (retombée seule) - kN
La méthodologie consiste à appliquer le principe courant de la conservation des sections planes et à calculer l'équilibre (élastique) des efforts internes. 1. Le diagramme des contraintes est prolongé pour obtenir la contrainte sur la fibre supérieure (dessus de dalle) 2. L’effort normal sur la section composée est nul : l’intégration des contraintes normales doit donner une résultante nulle, la largeur participante de hourdis s’en déduit 3. Tous les paramètres géométriques et de contraintes sont déterminés, il ne reste alors plus qu’à calculer le moment résultant du diagramme des contraintes.
Application au cas de la section sur appui :
On note une largeur de table réduite (47 cm), ce qui est logique compte tenu de l’effet de traînage de cisaillement. As=14.4 cm² (calcul aux ELU).
Application au cas de la section en travée :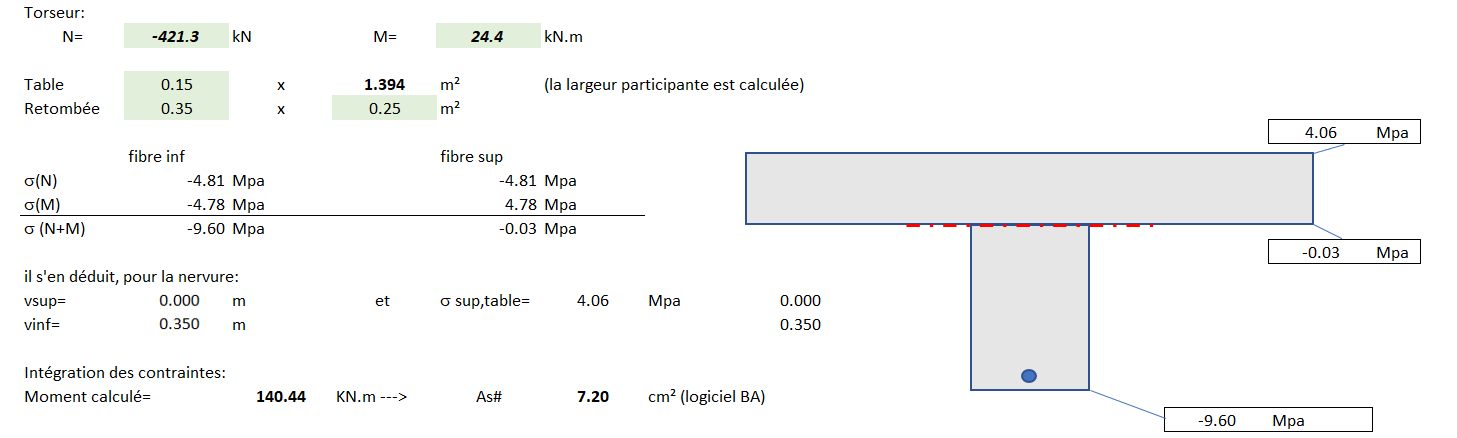
On note une largeur de table plus conséquente (139 cm), valeur logiquement plus importante que sur appui. As=7.20 cm² (calcul aux ELU).
Si on effectue un calcul automatisé dans la nervure et dans la dalle :
→ Le logiciel propose des sections d’armatures à des localisations qui, de fait, n’en nécessitent pas lorsque l’on effectue un calcul de béton armé «manuel» (il a bien été vérifié en parallèle qu’aucune section d'acier comprimée n’était nécessaire).
→ Dans le cas présent, l’approche automatisée conduit à un très léger déficit d’armature inférieure en travée et un surplus d'armature en fibre supérieure.
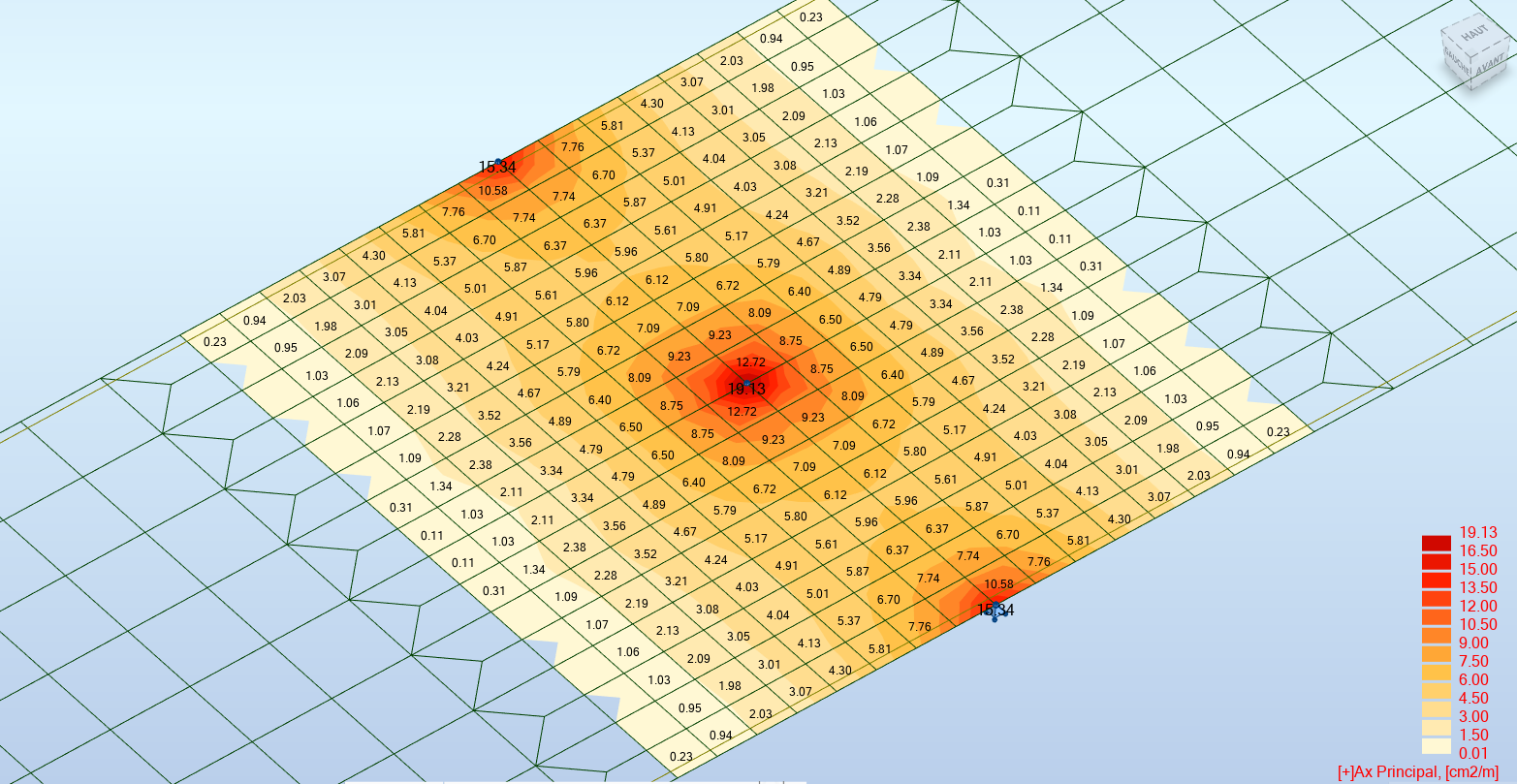
Cartographie des armatures en fibre supérieure du hourdis
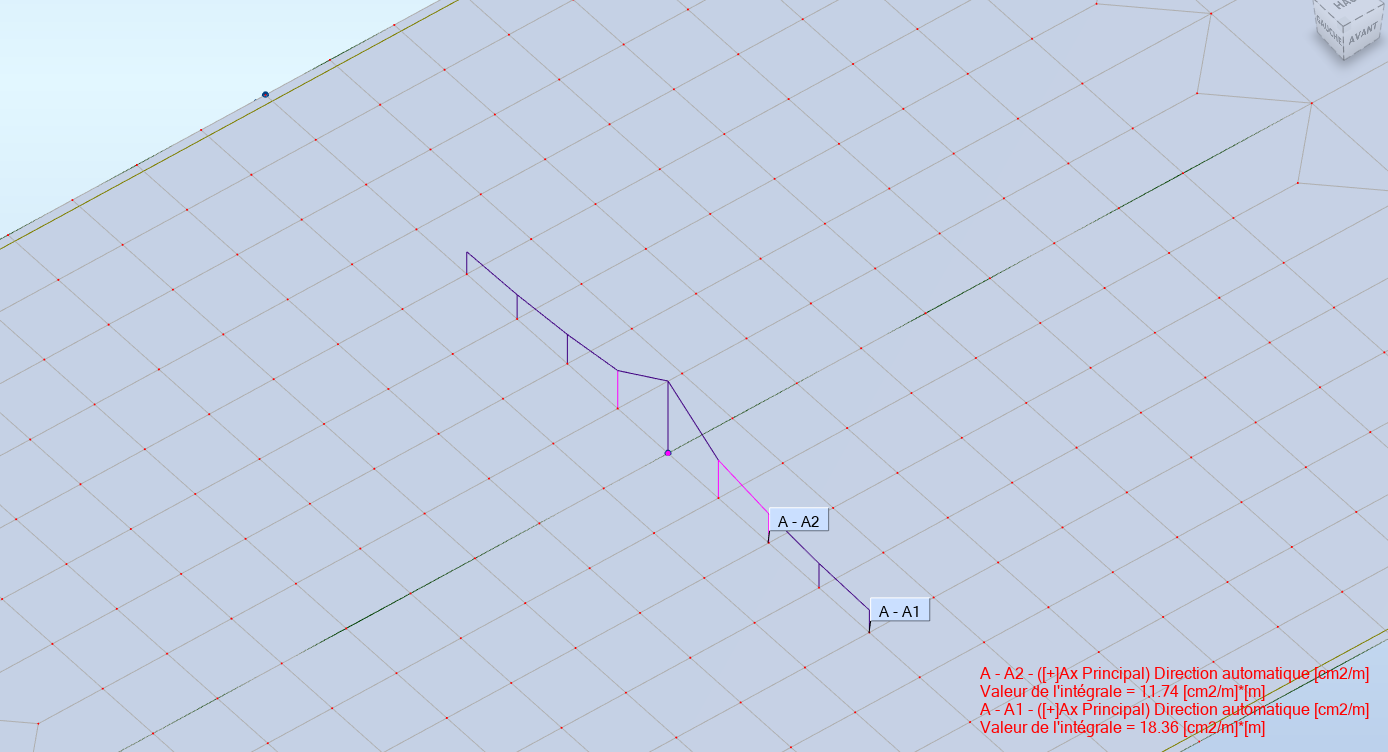
Armatures en fibre supérieure du hourdis sur l'appui central, poutre centrale (18.36 cm² sur 2 m)

Armatures en fibre inférieure du hourdis
Les efforts calculés via le modèle en grillage de poutres sont les suivants et conduiraient à 7.2 cm² en travée et 15.4 cm² sur appui: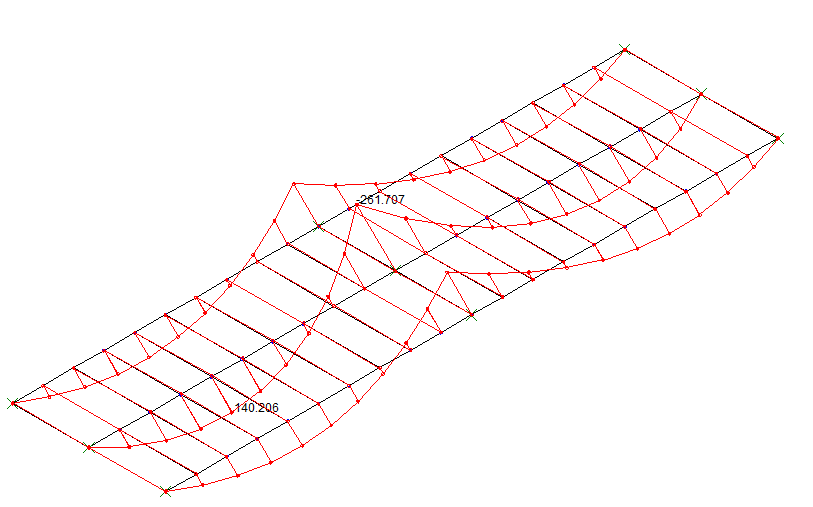
Modèle grillage de poutres (Mt = 140 kN.m, Ma = -262 kN.m) - sans prise en compte des largeurs participantes
En conclusion, sur l'exemple ci-dessus, on se rend compte que le calcul automatisé du ferraillage n'est pas satisfaisant. Sans considération de % mini, il conduit à placer des armatures dans des zones où un calcul réglementaire n'en demanderait pas et à sous et sur-armer certaines zones. En sus, rappelons encore un fois que le calcul automatisé ne tient compte ni d'un décalage de la courbes des moments, ni du poinçonnement, ni des bielles d'about… Il appartient, encore une fois, à l'ingénieur d'analyser les résultats et de tenir compte ou non de certains d'entre eux. Notons que la problématique de lissage des efforts ou des armatures se pose à nouveau en cas d'utilisation d'EF de type dalle ou coque.
D'autres exemples sont donnés en Exemple C - Modélisation de grillages de poutres.
C.8.3 Poutres et dalles mixtes acier-béton
En règle générale, on modélise le caractère composé des sections. Dans certains cas, toutefois, la modélisation peut se limiter à la poutre principale seule, sans tenir compte du phasage, par exemple, pour un prédimensionnement. Après calculs, les sollicitations de la poutre métallique sont alors utilisées pour venir dimensionner et vérifier le comportement de la poutre mixte selon le référentiel réglementaire approprié. Le modèle ne détecte pas que c'est une poutre mixte et il y a une petite erreur sur la raideur dont il faut évaluer l'acceptabilité.
Lors de la justification réglementaire de la poutre, il conviendra de tenir compte du caractère mixte et du phasage de construction.
Approches de modélisation :
Pour un calcul plus rigoureux, il est possible de modéliser la poutre mixte :
-
soit sous forme d’une poutre dont les caractéristiques mécaniques tiennent compte de la connexion de l'acier et du béton. Pour cela, on appréhende la différence des modules d'Young des deux matériaux via un coefficient d'équivalence - on dit dans cas qu'on homogénéise les matériaux, généralement en ramenant le béton à une équivalence métal. (a)
-
soit par deux poutres superposées, l'une, inférieure, métallique, l'autre, supérieure, en béton, à l'altimétrie de leur centre de gravité respectif. Ces barres sont reliées à leurs extrémités par des liaisons rigides. Ceci peut faciliter la prise en compte d’un retrait et d’un fluage différentiel. Si l'ouvrage est modélisé dans sa globalité, les barres longitudinales en béton décrites ci-dessus sont, en complément, reliées par des barres transversales de manière à former un “grillage” de poutre. (b)
-
on peut également choisir de remplacer les éléments de barres du hourdis par des éléments finis de type coques ( c). Dans ce cas, le calcul des torseurs nécessite un post-traitement, idéalement automatisé, suivant la méthode décrite en C.8.2.
Les approches (b) et ( c) sont à réserver à des cas particuliers, car, si dans un premier temps elles peuvent paraître plus simples, les pré- et post-traitements sont toujours beaucoup plus longs qu'avec un modèle de type (a), surtout si l'on utilise un logiciel dédié aux calculs mixtes.
Pour tenir compte du phasage, on doit, à chaque modification d'état, soit modifier l’inertie de la poutre homogénéisée (a), soit activer les poutres du hourdis (b) ou les coques ( c), par exemple dès lors que le béton a fait prise et est décoffré. Il faut bien sûr tenir compte du fluage du béton, soit à l'aide d'un coefficient d'équivalence, soit via une loi de fluage et des zones dites fissurées.
Exemple d'un ouvrage mixte modélisé suivant l'approche (a) :
Exemple d'un ouvrage mixte dont la dalle est modélisée par des éléments de coque excentrés - approche ( c). Les poutres métalliques sont dans ce cas modélisées strictement suivant la répartition matière (métal seul):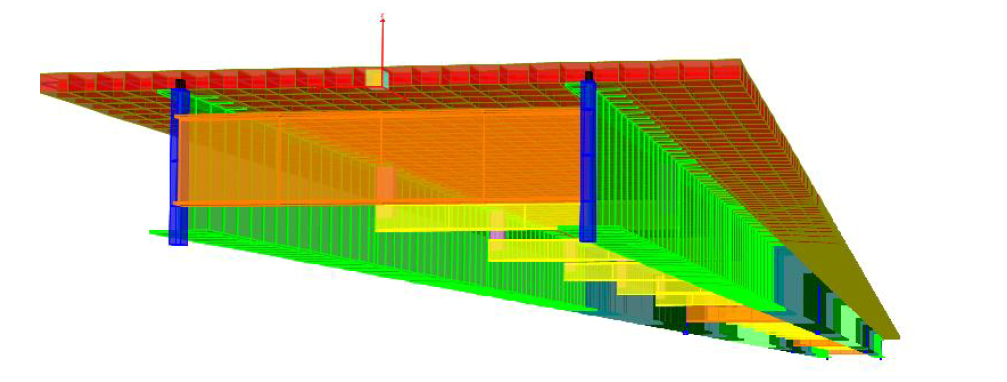
L'emploi d'un logiciel spécifiquement développé pour les calculs mixtes est toujours recommandé lorsque cela est possible.
Voir en Partie 3, l'exemple B - Bipoutres mixtes et métalliques.
C.8.4 Plancher mixte (bâtiment)
Un plancher mixte est composé de poutres métalliques supportant des dalles en béton armé (prédalles ou non) ou en bac acier métallique.
C.8.4.1 Charges pondérales et verticales : sens de portée des dalles
Les calculs des efforts dans un plancher mixte sont réalisés en considérant la résistance des poutres métalliques seules. Le béton est alors considéré comme un poids mort non résistant. De plus généralement ces planchers sont constitués de bacs aciers collaborants qui ne portent que dans un seul sens. Ces particularités nécessitent des dispositions spécifiques dans les modélisations.
Dans le cas de géométrie simple, la dalle en béton n’est pas modélisée et les charges sont appliquées directement sur les profilés métalliques.
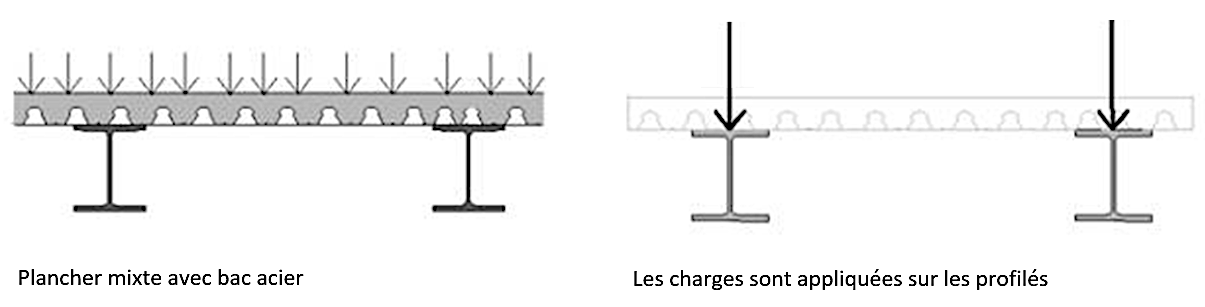
Lorsque la géométrie est complexe, la répartition manuelle des charges sur les profilés devient trop délicate, il faut alors faire appel aux calculs des répartitions des charges par le logiciel en utilisant les surfaces de répartition. Les logiciels les plus courants possèdent ce type d’élément qui se comporte comme une plaque d’épaisseur très faible, sans rôle résistant mais répartissant les charges sur les poutres porteuses. Des options permettent de prendre en compte les sens de répartition des bacs aciers, mais cela demande une grande attention afin de bien respecter les sens porteurs, les vérifications sont indispensables. Prenons l’exemple des pétales de la fondation LUMA à Arles constituées de plancher mixte avec bac acier, elles sont représentées en bleu dans le schéma ci-après …
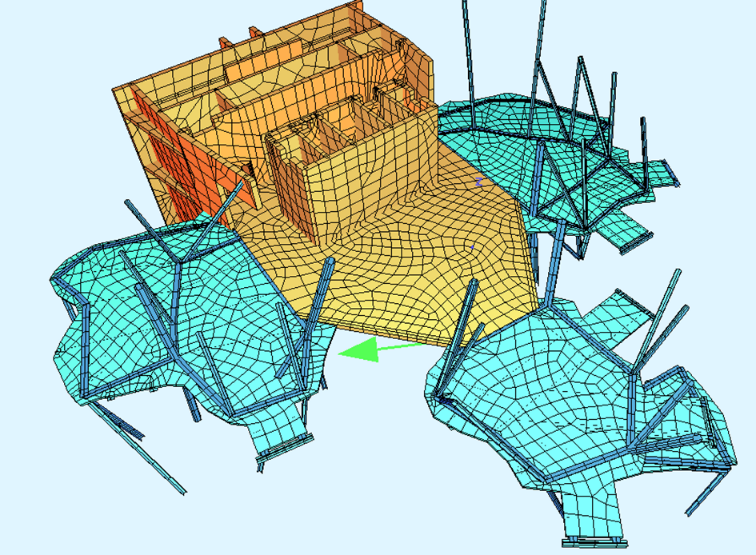
Les surfaces de répartition en bleu sont maillées comme des dalles, mais ne participent pas à la résistance de la structure.
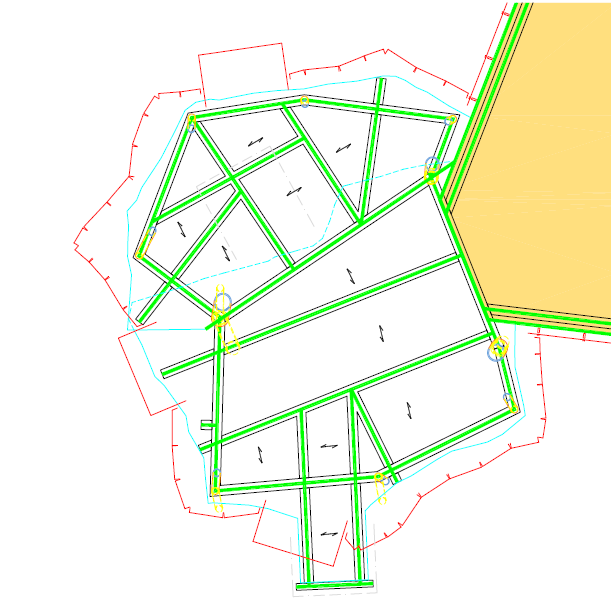
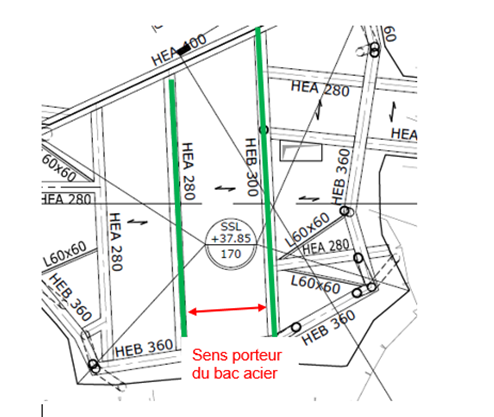
Vue en plan du plancher avec le sens porteurs des bacs acier

Visualisation des chargements des poutres calculés directement par le logiciel
Les calculs sont ensuite menés classiquement.
Le calcul des dalles en tant que tel se fait alors par un calcul spécifique de dalle (orthotrope) entre poutres.
C.8.4.2 Charges horizontales (vent, séisme)
Dans les cas usuels, la dalle en béton est désolidarisée des porteurs afin de ne pas participer au contreventement du plancher. Ce dernier est alors assuré par des contreventements horizontaux métalliques.
Mais dans certains cas complexes, il peut être nécessaire de contreventer les planchers en utilisant la dalle en béton. La modélisation devient alors très complexe :
-
la dalle doit être modélisée avec une excentricité par rapport à la fibre moyenne des profilés ;
-
il est nécessaire de modéliser les connecteurs entre la dalle et les profilés ;
-
le nœud de jonction dalle/poteau est différent du nœud de jonction profilés/poteau.
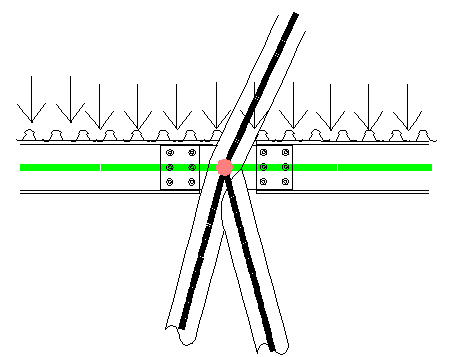
Plancher mixte sans modélisation de la dalle - Contreventement assuré par les profilés
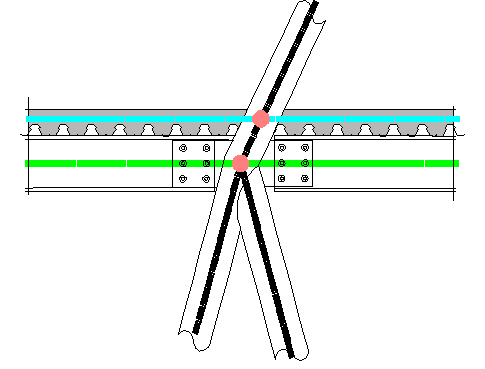
Contreventement assuré par la dalle
$translationBooksC.9 Matériaux
C.9 Matériaux
Le chapitre 4 de la partie 1 est dédié aux matériaux du génie civil et à leurs spécificités.
La définition des matériaux est une partie plutôt simple de la modélisation, car la plupart des logiciels ont des lois de matériau prédéfinies, suivant un ou plusieurs règlements.
Ces lois correspondent à une « courbe » simplifiée du comportement contraintes-déformations du matériau, considéré comme élastique et linéaire et intégrant des coefficients minorateurs de sécurité (sur le module et sur la résistance limite). Certains problèmes très particuliers peuvent nécessiter l’introduction d’une courbe plus complexe (loi de Sargin par exemple), ce que permettent, en principe, tous les logiciels.
En cas d’utilisation des lois prédéfinies, pour le béton, on veillera à bien intégrer le fait que le module d’Young de calcul est généralement par défaut le module à court terme. Pour les effets long terme, pour certains calculs thermiques et pour les calculs sismiques, il faudra penser à corriger le module. C’est valable également pour les calculs phasés où le module varie en fonction de l’âge du béton.
De la même manière, le logiciel prend un coefficient de Poisson par défaut. Généralement υ=0,2 pour le béton et υ=0,3 pour l’acier. Certains règlements demandent de prendre un coefficient υ=0 pour le béton à l’ELU. En particulier, voir le BAEL et le §3.1.3 (4) de l’Eurocode 2.
Pour tous les calculs en RDM qui nécessitent la prise en compte de la fissuration du béton (sismique, second ordre, dalles de ponts mixtes …), il faut tenir compte de la loi moment courbure de la section fissurée, qui représente l’affaiblissement de la section et la raideur réelle de la structure. Parfois, le code fournit des règles simples d'adaptation des inerties. Cela pourra nécessiter des calculs itératifs, d'abord en inertie non fissurée pour déterminer les zones de fissuration, puis avec prise en compte de l’inertie fissurée.
Il est à noter que certains logiciels permettent de prendre en compte directement une inertie fissurée.
$translationBooksC.10 Comportement spécifique au cisaillement et à la torsion
C.10 Comportement spécifique au cisaillement et à la torsion
De manière générale, il convient de noter que les modélisations filaires ne prennent pas systématiquement en compte les déformations d'effort tranchant, ni de manière appropriée les déformations de torsion.
Toutefois, dans le cas d'une modélisation d'une structure sensible sur ce point, il faut veiller à activer l'option de prise en compte des déformations d’effort tranchant et de torsion et à bien définir les sections réduites et inerties de torsion.
On peut noter également que les phénomènes de torsion gênée sont impossibles à modéliser en filaire, car les éléments poutres de RDM sont bâtis sur une hypothèse de conservation des sections droites (sans distorsion ni gauchissement) et pourtant, leur prise en compte conduit à des distribution de contraintes différentes de celles calculées en RDM “classique”.
La prise en compte de la torsion gênée demandera en général la modélisation séparée de tous les plaques constituant le profil mince de la section.
Quelques exemples de structures sensibles à ces phénomènes :
-
pour le tranchant : poutres PRS élancées (poutres de bipoutres mixtes, par exemple), structure de type console (voiles de contreventement avec un ratio hauteur/longueur faible). La non prise en compte de la déformation de tranchant aboutira, dans le premier cas, à des déformées sous-évaluées conduisant à une contreflèche erronée et, dans le second cas, à des raideurs sur-évaluées ;
-
pour la torsion : structures non libres de se distordre (en un ou plusieurs points).
Comparaison de calculs de l’angle de rotation d’une poutre en console en I
Données - poutre en console :
-
Conditions aux limites : encastrée en x=0 (θ=0, θ'=0) et libre en x=L (B=0, T=0)
-
Longueur : L = 1 m
-
Chargement : moment de torsion à l’extrémité x=L : Mx = 10 kN.m
-
Section : PRS ht = 200 mm, bt = 200 mm, tf = 20 mm, tw = 10 mm
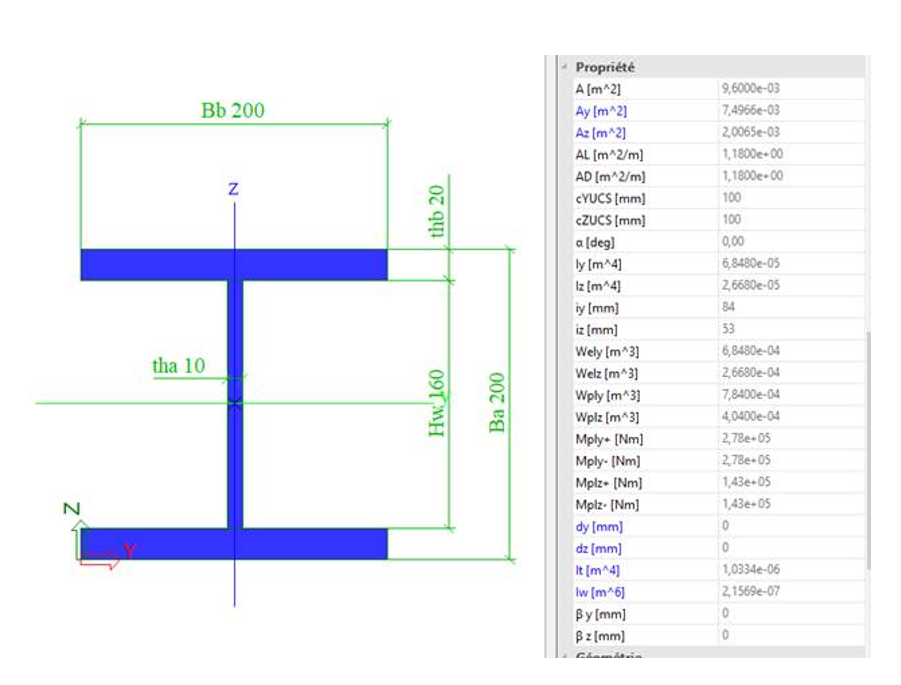
Modèle éléments plaques
Chargement :
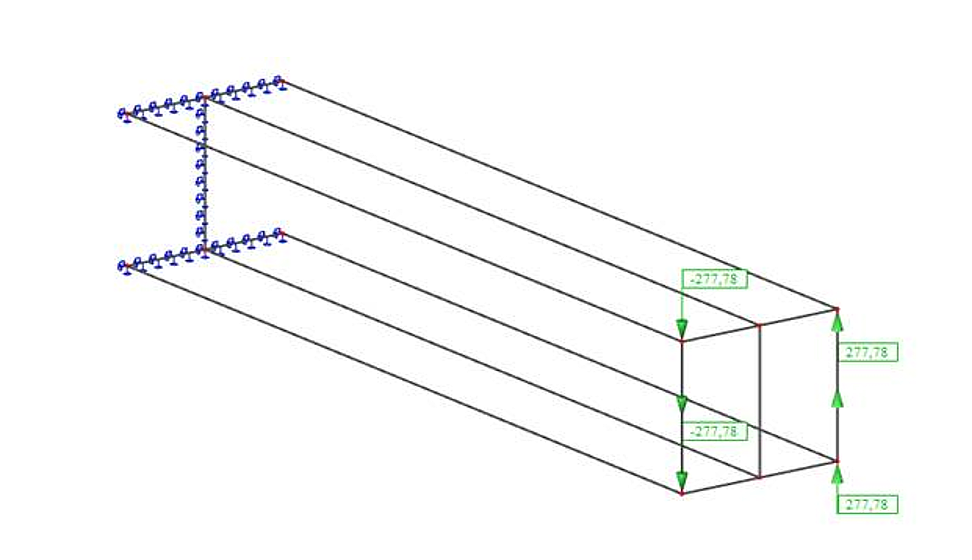
Résultante:
Déplacement θ(L)=0.042 rad
Modèle élément filaire
Chargement :

Résultante:
Déplacement θ(L)=0.1198 rad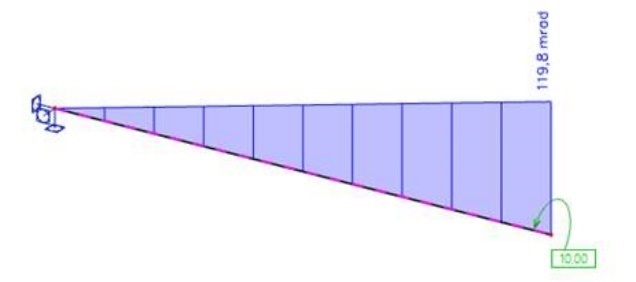
Calcul analytique
L’équation différentielle de l’angle de rotation est donnée par :
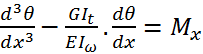
Avec les conditions aux limites donnée au paragraphe précédent, la solution de cette équation est :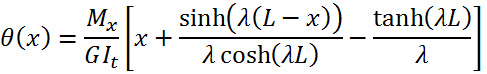
Avec :
-
It : inertie de torsion de St Venant
-
Iω : inertie sectorielle
-
Mx : moment de torsion
-
L : longueur de la poutre
-
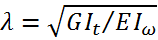
Application :
-
L = 1 m
-
G = 80 770 MPa
-
E = 210 000 MPa
-
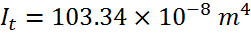 (calculé par le logiciel)
(calculé par le logiciel) -
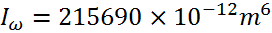 (calculé par le logiciel)
(calculé par le logiciel) -
Mx = 10 kN.m
-

![]()
Le calcul analytique et le modèle éléments surfaciques donnent le même résultat de rotation θ(L)=0.042 rad.
Le calcul de modèle élément filaire donne un résultat 2.85 fois supérieur.
Dans le modèle élément filaire , la raideur due à l’inertie de gauchissement n’est pas prise en compte pour le calcul de l’angle de rotation :
![]()
Conclusion
En règle générale, pour les modèles en élément filaire, les raideurs dues à la torsion d’une poutre en section ouverte ne sont pas bien prises en compte dans les calculs.
En cas de doute, une approche par éléments de type coque, sur un modèle simplifié, global ou local peut aider à cerner les effets.
$translationBooksC.11 Modélisation des charges
C.11 Modélisation des charges
Comme expliqué dans le chapitre E, il convient de toujours vérifier cas de charge par cas de charge (permanentes, d’exploitation et thermiques), par une somme manuelle des charges , le torseur global des charges : résultante en force mais aussi en moment. (Les logiciels dans leur grande majorité permettent de sortir le torseur global).
C.11.1 Penser aux cas de charge tests
Il est important, dès la modélisation achevée, de prévoir des cas de charges tests qui permettent de valider le bon comportement d’ensemble du modèle.
On pourra par exemple prévoir des forces unitaires uniformément reparties selon les 3 directions, des forces unitaires ponctuelles et en complément des variations de température. Et pour ces cas de charges, on examinera les déformées (ordres de grandeurs usuels en génie civil, discontinuités cinématiques ou de maillage, …) et les réactions d’appui (toutes forces supposées appliquées doivent se retrouver dans les réactions).
Ces tests permettent ainsi de vérifier les raideurs, les conditions aux limites et les liaisons internes. Ils permettent également ensuite de vérifier les cas de charge plus complexes (ordre de grandeur des effets).
C.11.2 Le cas du poids propre
La plupart des logiciels permettent de prendre en compte automatiquement un poids propre calculé à partir des sections des éléments et du poids volumique du matériau.
Cette méthode directe doit faire l’objet d’une vérification systématique. En particulier, les simplifications géométriques nécessaires à la modélisation peuvent induire un poids propre différent de celui calculé à partir des plans. Une approche manuelle rigoureuse des métrés ne devrait pas conduire à un écart supérieur à 5 %. Quoi qu’il en soit, tout écart doit toujours pouvoir être justifié.
Dès que les sections résistantes s’éloignent des sections brutes de la structure (par exemple en cas de prise en compte de la fissuration, du traînage de cisaillement ou de sur-épaisseurs sacrificielles), il convient de redéfinir le cas de charge Poids propre sans l’option automatique ou de redéfinir des caractéristiques de matériaux qui en tiennent compte, groupe d’éléments par groupe d’éléments.
C.11.3 Charges surfaciques et charges linéiques
Les charges surfaciques sont généralement appliquées sur la fibre moyenne de l’élément de plaque. Il faut tenir compte, dans l’intensité et le périmètre de cette charge surfacique, de la diffusion des charges jusqu’à la fibre moyenne, en intégrant l’éventuelle diffusion au travers de l’épaisseur du revêtement.
Par ailleurs, il faut vérifier si la charge surfacique est appliquée suivant la normale à l’élément (repère local) ou selon le repère général du modèle.
Certaines charges (neige par ex.) sont définies par rapport à une surface de référence (l’horizontale pour la neige), il convient donc d’en tenir compte dans l’application à des surfaces non parallèles à ce plan de référence (cas de la toiture inclinée pour la neige). Souvent dans les logiciels, il faut préciser explicitement si une charge est projetée ou non.
D’autres types de charges (vent, pression hydraulique, …) sont quant à elles toujours perpendiculaires aux surfaces.
Enfin, on vérifiera toujours l’orientation des charges et comme pour le poids propre, les déformations et les réactions d’appui.
Voir les exemples ci-dessous.
Exemple de la buse avec chargement de la poussée des terres
Problématique : modéliser une charge linéique, sur une surface inclinée.
Les logiciels proposent des options lors de la définition du chargement, qui ne sont parfois pas très explicites.
Cas 1 : Charge définie dans le repère global utilisateur
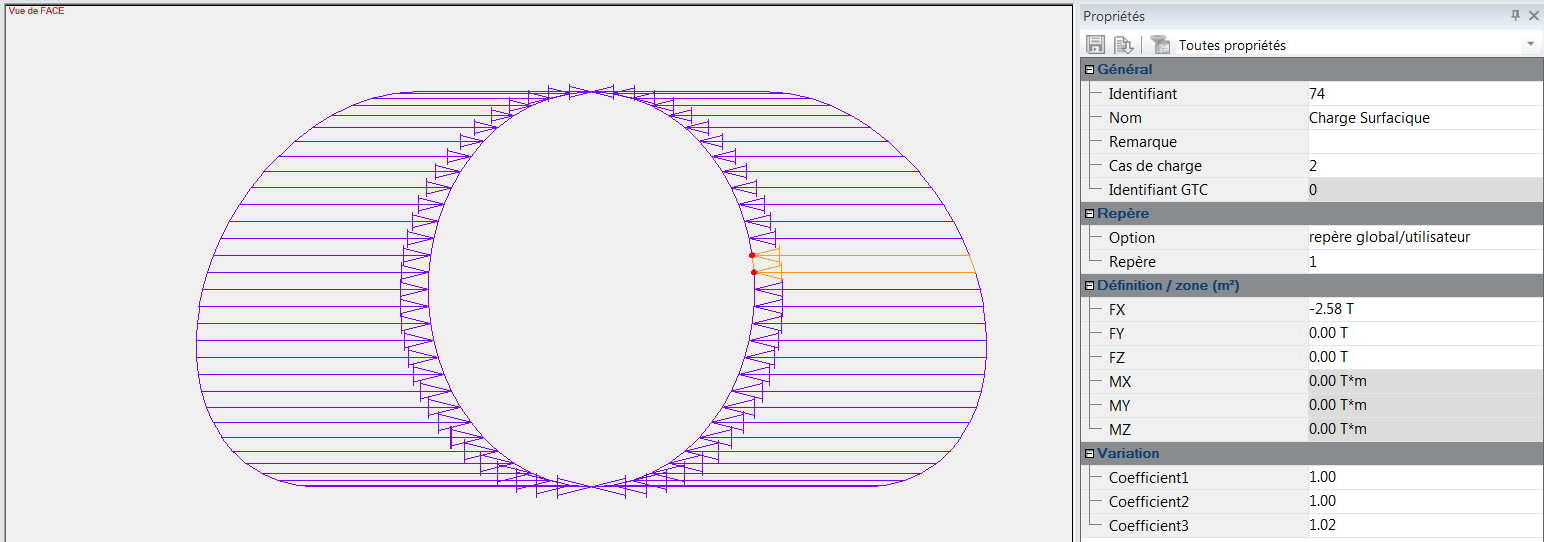
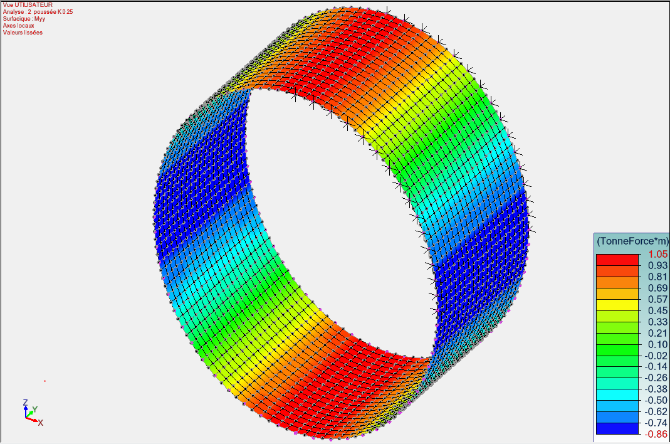
La charge introduite sur la barre, est définie comme une charge horizontale au mètre linéaire de l’élément.
Cas 2 : Charge définie dans le repère projeté
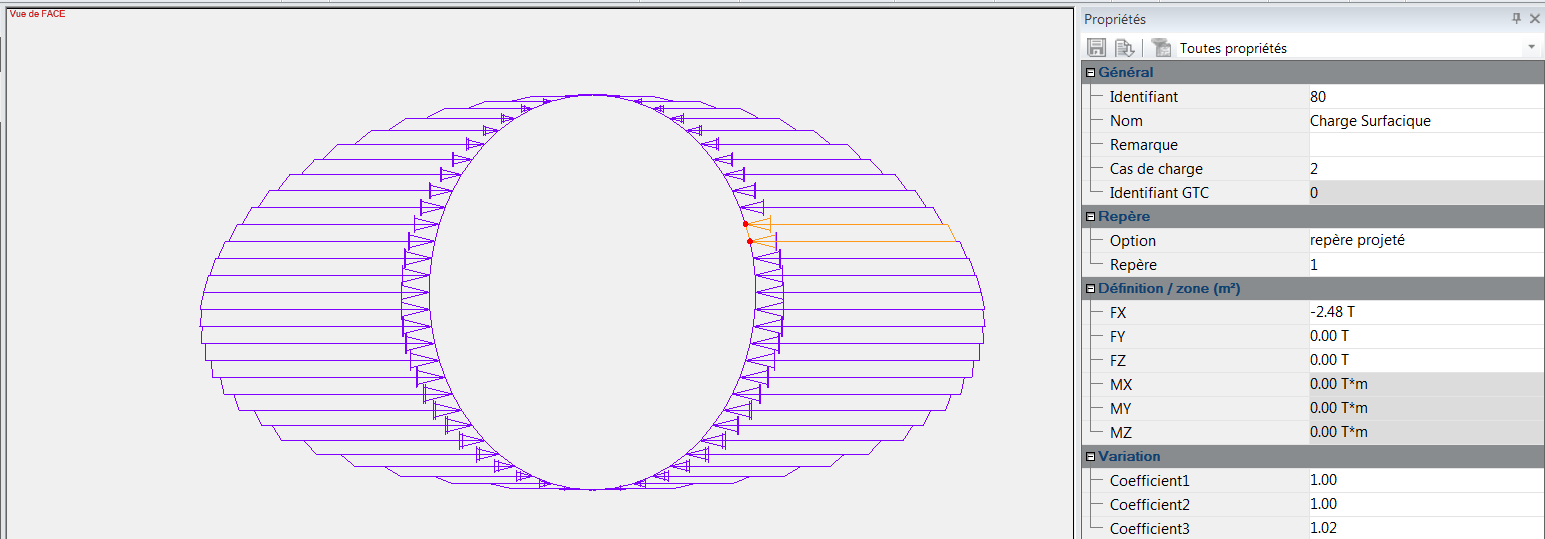

La charge introduite sur la barre, est définie comme une charge horizontale au mètre linéaire mesuré perpendiculairement à l’action de la charge (une verticale dans le cas présent).
Conseil : Toujours vérifier, sur un exemple simple, que l’option utilisée correspond bien à la modélisation de chargement souhaitée.
Les charges linéaires sont également concernées par ces problèmes de diffusion et de repère.
Nota : dans le cas d’une poussée des terres, la modélisation à utiliser est la seconde, à savoir une projection des charges sur un plan vertical.
C.11.4 Charges thermiques
Les charges thermiques sont constituées de deux types de charges :
-
Les variations linéaires dont un cas particulier très courant est la variation uniforme,
-
Les gradients de températures qui proviennent d’une différence de température entre les surfaces extrêmes d’une structure.
Il est indispensable d’utiliser des cas test pour vérifier la prise en compte correcte des phénomènes thermiques en cohérence avec le bridage de la structure.
Il est à noter que les charges thermiques ne créent des efforts (ou des contraintes) uniquement si la structure n’est pas libre de se déformer (bridages, structures hyperstatiques, …)
La fissuration du béton peut jouer un rôle important dans la distribution des efforts (voir 11.5 ci-après).
C.11.5 Modélisation du retrait et du fluage
A défaut d’une option spécifique du logiciel, la modélisation du retrait du béton peut être réalisée par l’application de cas de charge thermique équivalents.
La modélisation du fluage peut être réalisée par des cas de charges thermiques ou réduction du module élastique des matériaux.
Il convient de bien vérifier que les déformations imposées sont conformes au phénomène attendu.
En cas de doute, il est toujours possible de réaliser des calculs en fourchette, pour encadrer le court et le long terme (cas des ponts mixtes, des fondations, …)
Description détaillée: modélisation du retrait dans les ponts mixtes
Lien vers la modélisation du retrait dans les ponts mixtes
C.11.6 Charges mobiles
La compréhension du concept de ligne d’influence est fondamentale pour la bonne appréhension des positionnements des convois et permet d’éviter la constitution de cas de charges trop nombreux.
Dans le cas d’ouvrages complexes, le concept n’est pas facilement applicable, néanmoins on peut toujours générer des lignes d’influence en plaçant des forces unitaires aux différents nœuds de la structure. Les résultats, une fois post-traités, avec un tableur par exemple, permettent alors de placer les charges tant surfaciques que mobiles pour produire l’effet le plus défavorable.
Les règlements définissent très fréquemment des modèles de charges qui combinent des charges de différentes natures avec des règles de concomitance et de configurations géométriques précises. Il convient de les lire attentivement et intégralement. Ceci permettant alors grâce aux lignes d’influence de positionner les charges à la position défavorable pour l’effet étudié (flèches, efforts, …).
Chargements suivant les lignes d’influence.
Cas des charges réparties sécables et des convois avec espacement variable des véhicules
A notre connaissance, tous les règlements imposent de charger les structures suivant les lignes d’influence. Les pratiques métier ou la phase dans laquelle se trouve le projet (EP, AVP, voire PRO) peuvent conduire à des simplifications : chargement de deux travées contigües, chargement de travées complètes en alternance (« une sur deux ») …
Dans le cas des ouvrages d’art, et en particulier pour les calculs d’Exécution, le chargement par lignes d’influence est obligatoire, et on ne peut pas se contenter de charger des travées complètes ou de faire circuler des convois à touche-touche.
Il convient donc de s’assurer que le logiciel utilisé est bien capable d’effectuer des calculs suivant les lignes d’influence (LI), c’est-à-dire d’adapter les longueurs chargées ou d’adapter le nombre et l’espacement des véhicules d’un convoi pour obtenir la situation la plus défavorable, pour un effet recherché, par exemple le moment, la réaction d’appui ou encore une déformée, …
1) Charges de type UDL de l’Eurocode. Nous recherchons l’effort tranchant maximal (i.e. en valeur positive ou négative) à mi-travée d’un pont à deux travées égales (2×25 m) et de section constante. Nous savons que la ligne d’influence de l’effort tranchant à mi-travée a l’allure suivante :
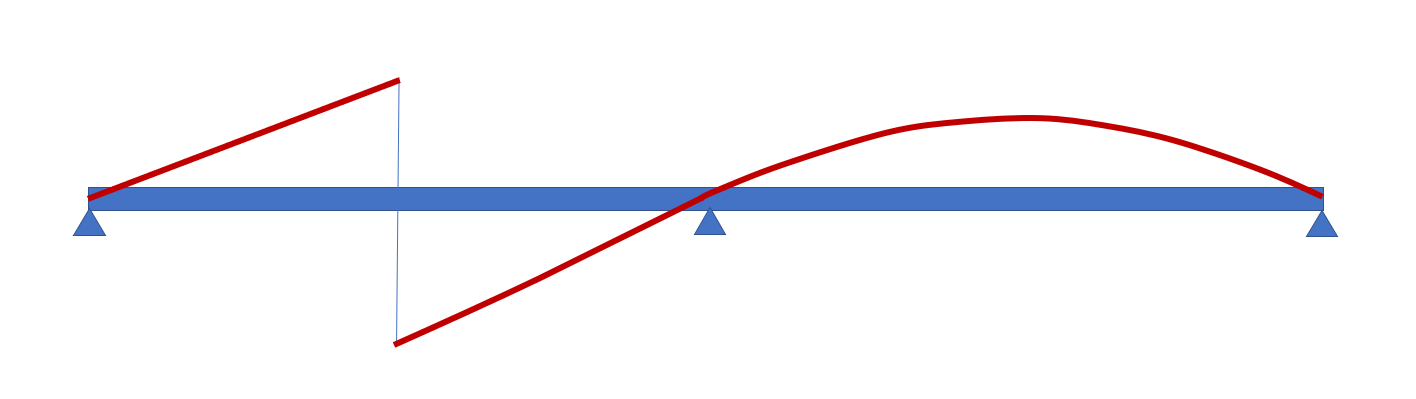
A défaut de mieux, on pourrait être tenté de charger une ou deux travées complètes.
Le diagramme ci-après montre, pour une charge unitaire de 10 kN/m, l’enveloppe des tranchants pour les cas :
-
Travée 1 chargée

-
Travée 2 chargée

-
Travées 1+2 chargées

A mi-travée 1, on obtient |V|max = 31.3 kN :
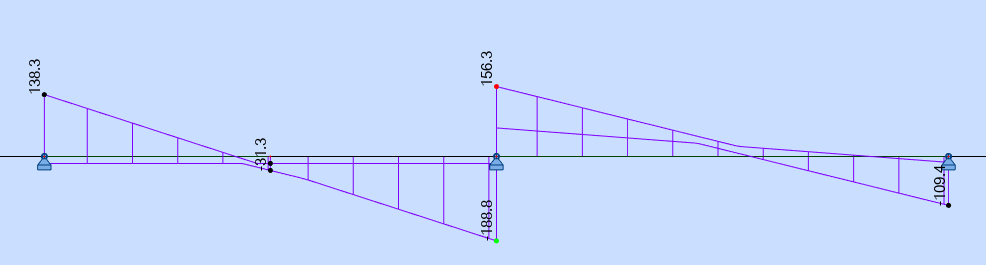
Le diagramme ci-après montre le même diagramme de tranchant, mais avec une poutre chargée suivant les LI :
-
Zone LI courbe supérieure
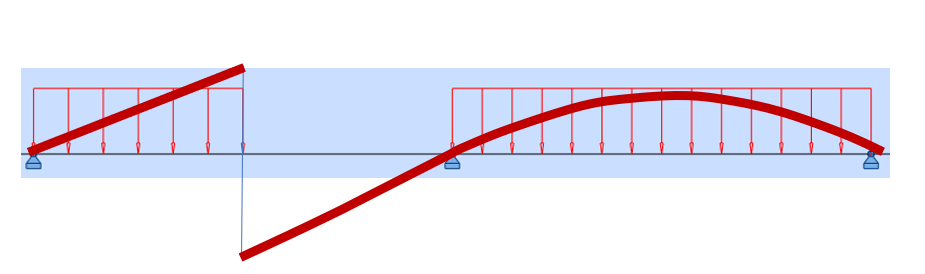
-
Zone LI courbe inférieure
On obtient |V|max = 53.7 kN, soit un écart relatif conséquent.
On pourrait répéter l’exercice pour toutes les sections.
Ceci était encore plus vrai pour les charges du fascicule 61 titre II, que nous sommes encore amenés à utiliser, lors de recalculs par exemple, il s’agit notamment :
-
Des charges réparties A(L) similaires à UDL, mais qui possèdent en plus la propriété de varier en intensité suivant la longueur chargée L,
-
Les convois B ou Mc, dont l’espacement peut varier, avec parfois une distance minimale à respecter. Le convoi Bc est décrit ci-après.
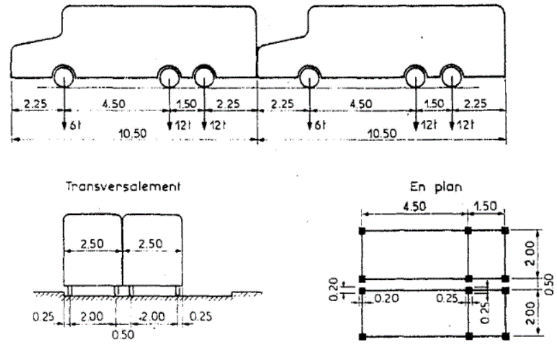
2) Illustration sur le pont précédent pour le cas du convoi Bc pour le moment sur appui
La ligne d’influence du moment sur appui a l’allure suivante :
Une étude fine serait à réaliser pour trouver la position précise des camions, mais on se rend immédiatement compte (ici pour des travées de 25 m - rappel) que les camions doivent être séparés pour obtenir un effet maximal :
Application : nous faisons circuler sur le pont deux convois, le premier, avec les deux camions à touche-touche, comme dessiné dans le règlement, et le second, avec une distance de 28.80 m environ (déterminé graphiquement).
Les résultats :
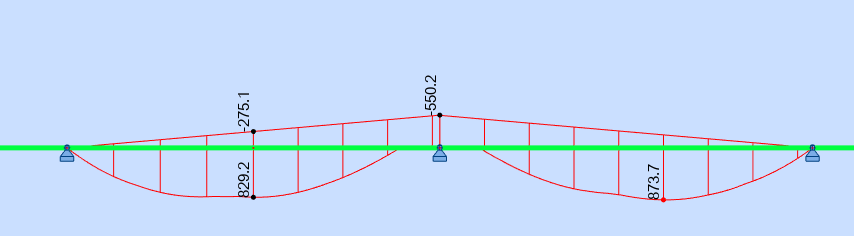
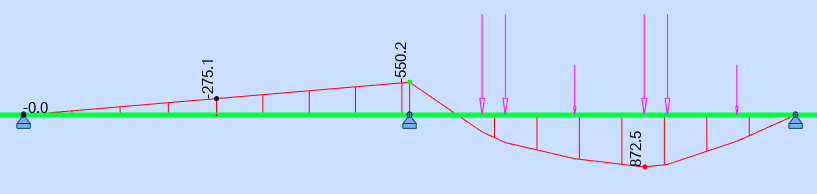
Camions à touche-touche, enveloppe et position défavorable.
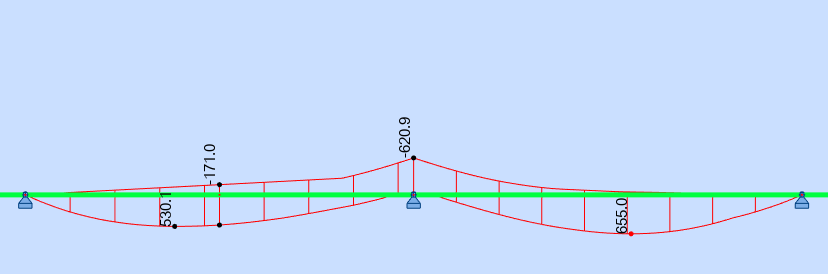
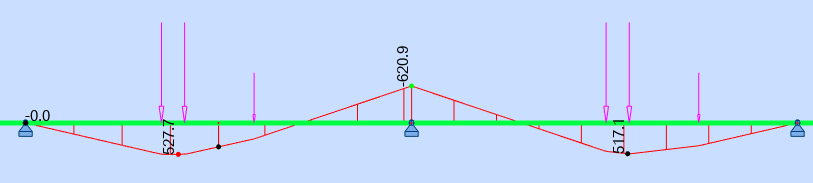
Camions séparés, enveloppe et position défavorable.
L’écart sur les moments sur appui est de l’ordre de 13%. A contrario, bien évidemment, le cas de charge utilisé pour obtenir le moment sur appui maximal n’est pas celui à utiliser pour les travées.
De manière pratique, on se rend rapidement compte que la détermination des longueurs chargées et/ou positions et espacements de convois, pour toutes les sections et pour toutes les valeurs d’intérêt, est une tâche titanesque à la main, et que l’aide du logiciel est indispensable – encore une fois pour des calculs de niveau EXE. Pour les autres phases, des calculs simplifiés, en conservant une certaine marge sur les justifications et les quantités reste possible, notamment en étudiant certaines sections judicieusement choisies sur l’ouvrage, mais ceci sort du cadre du présent document.
Ensemble des cas de charges et résultats pour les charges réparties. Travée 1, travée 2 et travées 1+2 :

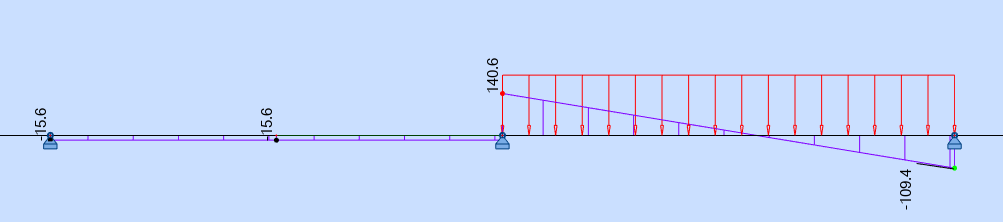
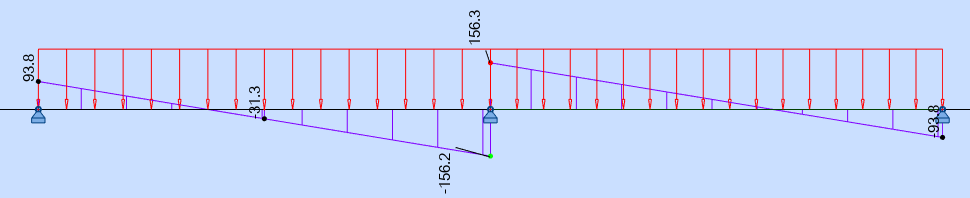
Chargements suivant Li :


C.11.7 Modélisation de la poussée et butée des terres
De manière générale, les actions générées par les sols (la poussée par exemple), les pressions d’eau ou encore les actions sismiques sont modélisées par des charges. Les réactions (pressions sur le sol, pouvant aller jusqu’à un seuil plastique, la butée, …) sont, elles, représentées par des ressorts linéaires ou non.
Les approches sismiques linéaires sont admises tant que le soulèvement des fondations est limité à 30% de la surface de ces dernières. Piège : on n’applique pas de forces de réactions sur une face bloquée par des ressorts… on laisse les ressorts faire le travail.
Nota : une approche en déplacements est également possible pour modéliser les charges de poussée et peut conduire à réduire les efforts globaux (cf. Guide AFPS / AFTES . GUIDE “Conception et protection parasismiques des ouvrages souterrains »).
$translationBooksC.12 Compléments liés aux éléments volumiques
C.12 Compléments liés aux éléments volumiques
Les principes énoncés pour les modélisations en 2D restent applicables en 3D, en particulier l’utilisation d’éléments isoparamétriques (parallélépipèdes plutôt que tétraèdres) est préférable, ce qui nécessite un lourd et rigoureux travail de préparation de la géométrie de base.
Les mailleurs automatiques sont à utiliser avec parcimonie.
Exemple d'un tablier de pont à poutres modélisé en EF volumiques:

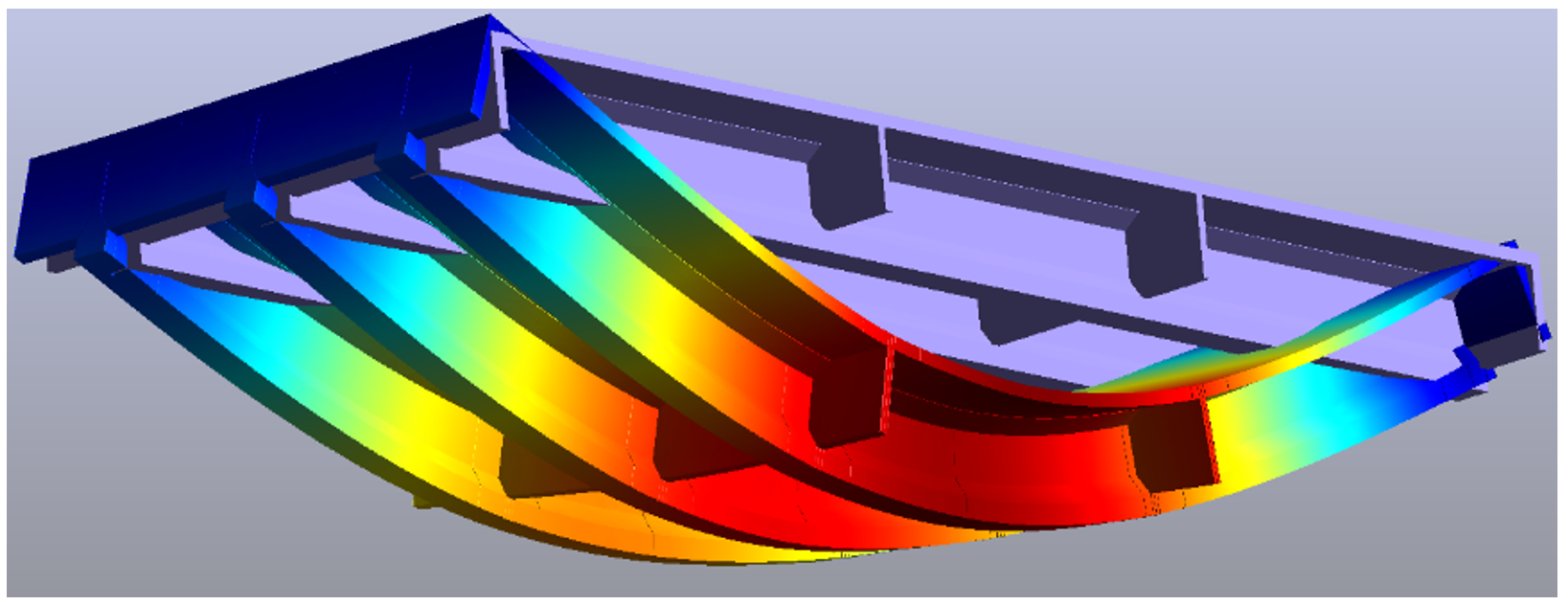
(Tiré de la Partie 3 - Exemple C - Modélisation de grillages de poutres).
$translationBooksC.13 Compléments liés aux calculs non linéaires
C.13 Compléments liés aux calculs non linéaires
Le présent paragraphe traite à la fois des non-linéarités liées aux lois des matériaux et des non-linéarités dites géométriques.
Il est fréquent d'associer les calculs non-linéaires à des structures complexes telles que les ponts à haubans et suspendus, pourtant ce sujet apparaît dans le quotidien de tout ingénieur structures, par exemple en cas :
-
de décollement partiel de semelles de fondations ;
-
d'incapacité de certaines barres à reprendre des compressions (voir le § C.2.7 sur les contreventements) ;
-
d'un calcul de flambement en béton armé ;
-
de cas de sortie du champs de la théorie des poutres (par exemple, le calcul des contraintes dans un contreventement de pont sous son poids propre).
De manière générale, pour tous les calculs non-linéaires, il est important d’effectuer un calcul linéaire avant de prendre en compte la non-linéarité pour comprendre le fonctionnement de la structure et l’effet spécifique de la non-linéarité.
C.13.1 Géométrie théorique et imperfections
La plupart des règlements imposent que les calculs non linéaires intègrent un défaut initial de forme ou d’implantation des éléments. Certains logiciels peuvent intégrer directement ce défaut. Pour d’autres, il faudra soit appliquer un cas de charge qui crée le défaut initial, soit définir la géométrie avec le défaut.
On peut noter que dans un calcul aux éléments finis, le recours à des éléments triangulaires permet toujours de tenir compte de la prédéformation d'une surface plane.
C.13.2 Haubans et câbles
Les haubans et câbles sont des éléments par essence non-linéaires, du fait de leur fonctionnement en traction seule et de l'effet de chaînette qui impose la prise en compte d'un module d'Young “apparent”. Ce module est fonction de la tension, de la longueur, de la masse volumique et du module d'Young brut du câble.
Pour les haubans, pour des phases amont de projet, il n’est pas toujours indispensable de prendre en compte ces deux effets ; on pourra alors modéliser le hauban par une barre, idéalement bi-articulée, en prenant soin de négliger le poids propre de la barre ou de l’appliquer directement manuellement aux extrémités. On vérifiera dans l’analyse des résultats que ces barres ne sont pas comprimées.
C.13.3 Zones de non-linéarité matériau
Un premier calcul linéaire permet de repérer les zones où l’on autorisera le comportement non linéaire. Le calcul se poursuivra par itérations successives en intégrant progressivement les non-linéarités.
C.13.4 Flambement et calculs en grands déplacements
-
Flambement - calcul des coefficients critiques
La plupart des logiciels sont capables de déterminer les charges critiques de flambement des barres comprimées (donc les longueurs de flambement des barres composant une structure) à partir d'un calcul modal, en petits, voire en grands déplacements. Il convient d'effectuer les calculs pour chaque combinaison dimensionnante. Un bon nombre de logiciels permettent également d'effectuer les vérifications normatives à partir de ce calcul des charges critiques (ou simplement via une introduction manuelle des longueurs de flambement).
Le calcul des coefficients critiques est basé sur la recherche des valeurs αi telles que le déterminant Det([Ko]+αi [Kσ])=0, où Ko est est la matrice de rigidité associée aux petits déplacements et [Kσ] la matrice de rigidité associée aux contraintes initiales.
L'objet n'est pas ici de développer toutes les possibilités offertes par les logiciels, mais d'insister (encore une fois) sur le fait qu'il convient de bien comprendre ce que fait son logiciel et quelle est l'incidence de la modification des paramètres de calcul. Un paramètre simple peut être tout simplement la subdivision nécessaire des barres pour obtenir les bons résultats, comme illustré dans l'exemple ci-après.
Illustration sur le portique contreventé du Chapitre C.2. Lien vers l'exemple du calcul des coefficients critiques de flambement.
Ce petit exemple confirme qu’il convient de maîtriser ce que fait l’outil et que, dès lors que l’on sort d’un calcul simple (calcul élastique linéaire, au premier ordre), il faut toujours se recaler sur des exemples simples et traités dans la littérature, par exemple.
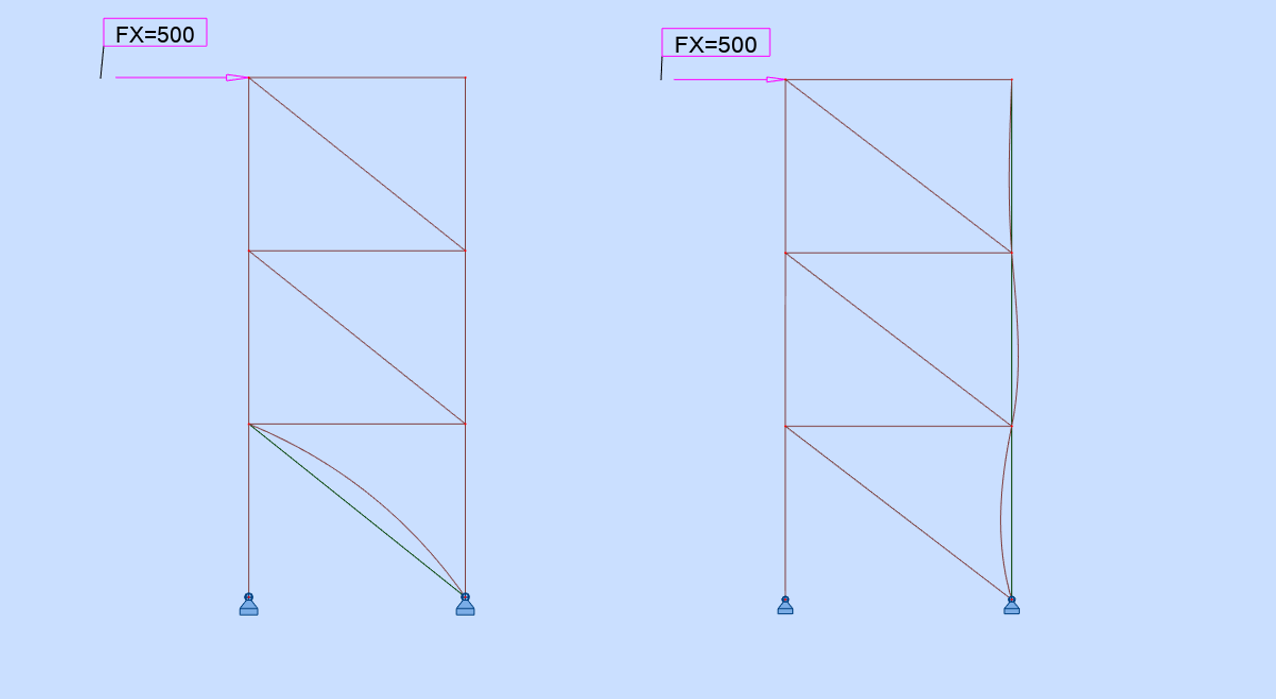
Déformées modales
-
Calculs en grands déplacements:
Ces calculs nécessitent la mise à jour des matrices de rigidité à chaque itération, que l'on soit en béton armé ou en métal. Ce qui est dit pour le calcul des coefficients critiques de flambement ci-avant quant à la maîtrise des paramètres du logiciel, reste parfaitement applicable.
Nous renvoyons à deux articles intéressants sur le sujet:
- Calcul au flambement des arcs - Comparaison entre un calcul approché et un calcul en grands déplacements du Bulletin Ouvrages d'art n°32“ - Lien vers l'article.
- Instabilité par flambement des arcs (CTICM) - Lien vers l'article.
$translationBooksC.14 Compléments liés au béton précontraint
C.14 Compléments liés au béton précontraint
La modélisation fine de la précontrainte nécessite l’utilisation d’un logiciel spécifique gérant les tracés des câbles, le calcul des tensions (calcul des pertes) et la prise en compte de phasages datés et des lois de fluage.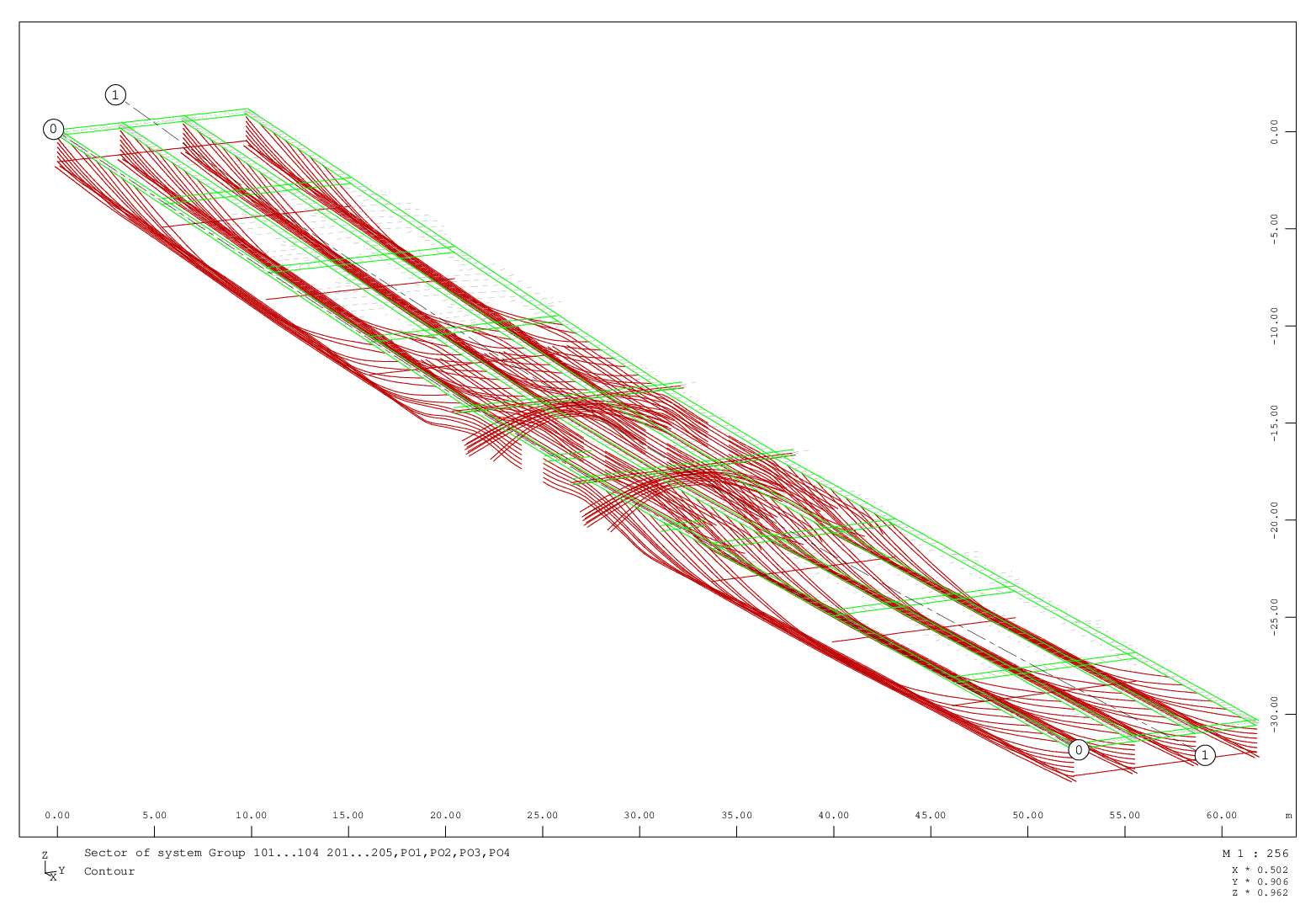 Exemple de câblage complexe
Exemple de câblage complexe
Il est cependant toujours possible, par exemple pour effectuer un calcul de prédimensionnement ou de vérification d’un calcul complexe, de modéliser la précontrainte de manière simplifiée.
Les poutres (et coques) doivent être décrites au niveau de leur centre de gravité pour garantir le bon positionnement des câbles dans la section.
Les deux sous-sections suivantes présentent la modélisation simplifiée d’un câble intérieur au béton puis d’un câble extérieur. Elle suppose la connaissance d’un tracé a priori et une tension constante dans le câble (après pertes instantanées ou à long terme, par exemple). Il est utile de préciser que la modélisation des pertes de précontrainte se ferait suivant la même logique mais avec un signe opposé à l’action de la précontrainte initiale.
C.14.1 Câble intérieur au béton

La méthode des forces externes permet d’appréhender les effets des câbles, en les modélisant comme des forces concentrées aux abouts et par des pressions (poussées) le long du câble.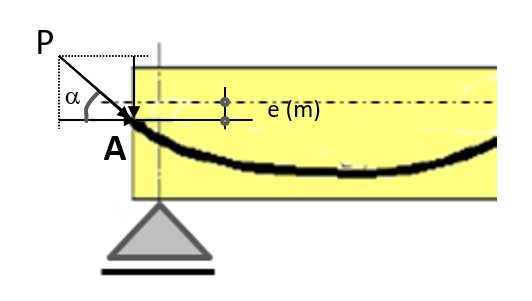
Ancrages d’abouts ou ancrages noyés, nous aurons :
-
un effort horizontal HA = P.cos(α)
-
un effort vertical VA = P.sin(α)
-
un moment MA = HA.e
(avec la convention de signes adaptée au logiciel)
Le long de la poutre, un câble exerce des poussées radiales, que l’on peut, dans le cas général, supposer verticales. Elles valent pi≈P/Ri. Il s’agit de la poussée au plein des câbles. Elles s’appliquent comme des charges réparties classiques.
Les segments rectilignes ne produisent pas de poussée (R=∞).
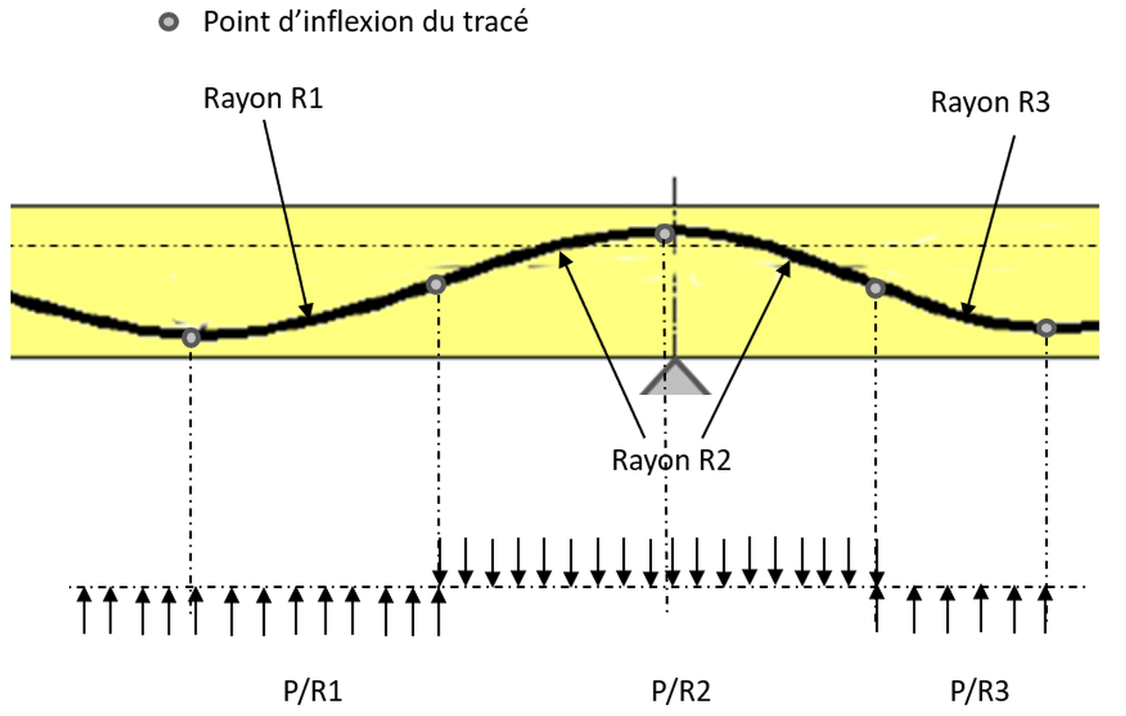
On confond fréquemment HA et P, cos(α) étant souvent proche de 1.00.
Exemple de définition manuelle simplifiée d'un câble.
La poutre comprend deux travées de 25 m. La section est symétrique et a une hauteur de 1.25 m (pour fixer les limites du câble).
Données d'entrées du câble.
On vérifie que le câble reste dans la poutre (la limite est fixée à 10 cm des faces supérieures et inférieures pour ce cas d'école) et que les raccords aux points d'inflexions ont bien la même pente.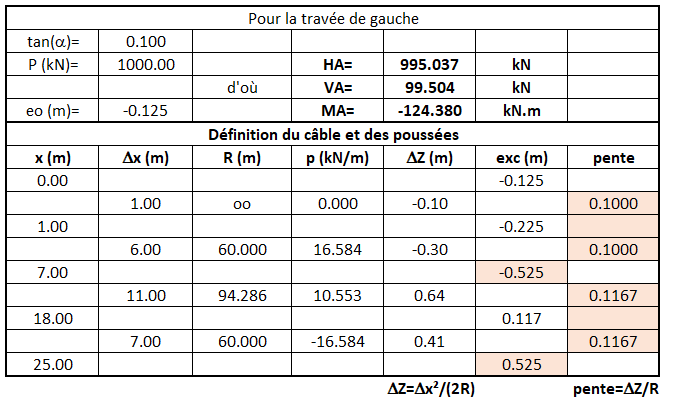
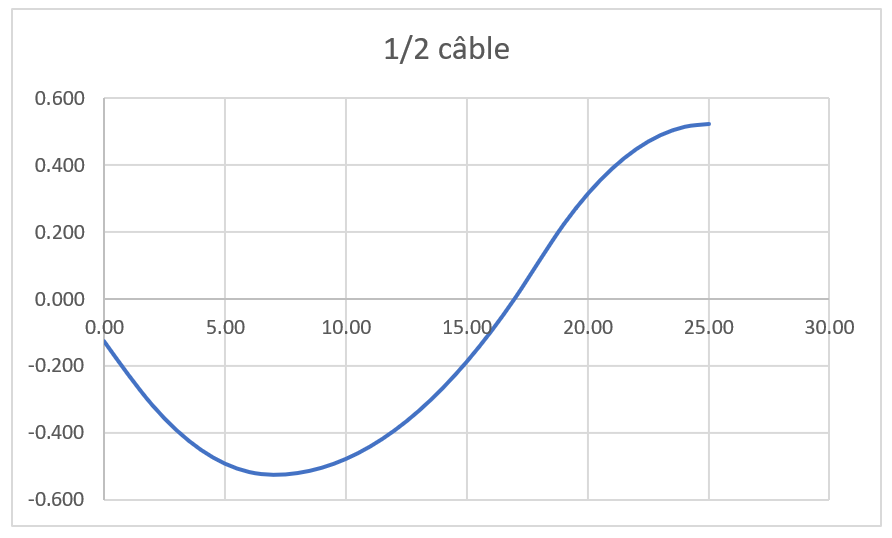
Traduit en chargement sur la poutre:
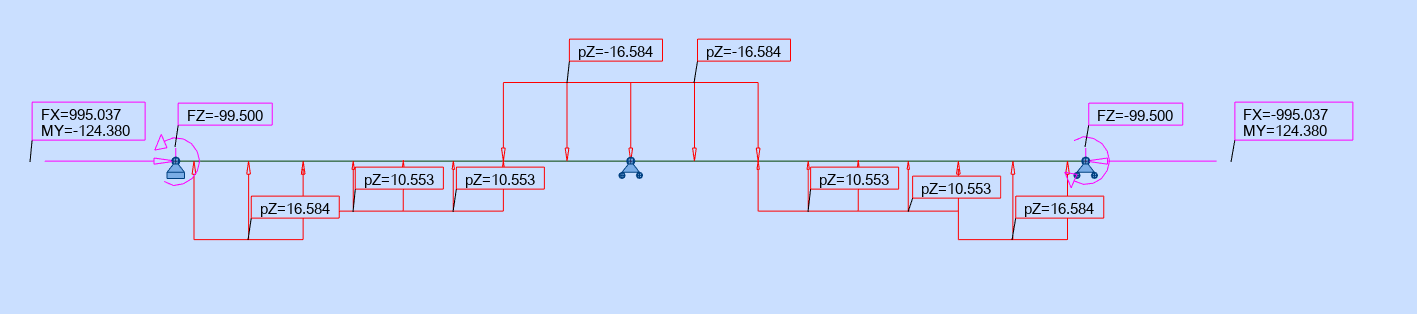
L'effort tranchant résultant, i.e. qui tient compte de l'hyperstaticité du système:
Le moment:
A des fins de contrôles, on peut :
-
toujours se ramener à un système isostatique (ici en supprimant l'appui central) ;
-
calculer le moment isostatique à mi portée (ou dans n'importe quelle section), par la somme des forces à gauche ou à droite. Les écarts ne doivent être supérieurs au % ;
-
sur cet exemple, vérifier que les résultats sont symétriques puisque la structure et la précontrainte le sont.
Courbe de tranchant “isostatique”:
Courbe de moment “isostatique” (la courbe divisée par HA est le tracé du câble):
On peut s’assurer que les réactions d’appuis du cas de charges précontrainte “isostatique” sont nulles: 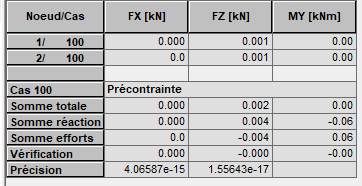
Calcul à l'aide d'un logiciel spécifique :
Cet exemple a été traité à l'aide d'un logiciel permettant de modéliser directement les câbles de précontrainte. La comparaison des résultats est disponible dans le document Exemple de précontrainte et excentrement.
C.14.2 Câble extérieur : forces aux ancrages et aux déviateurs
Comme ci-avant, en supposant une tension uniforme pour tout le câble, la méthode des forces externes permet d’appréhender les effets d’un câble de précontrainte en le modélisant comme une suite de forces concentrées.
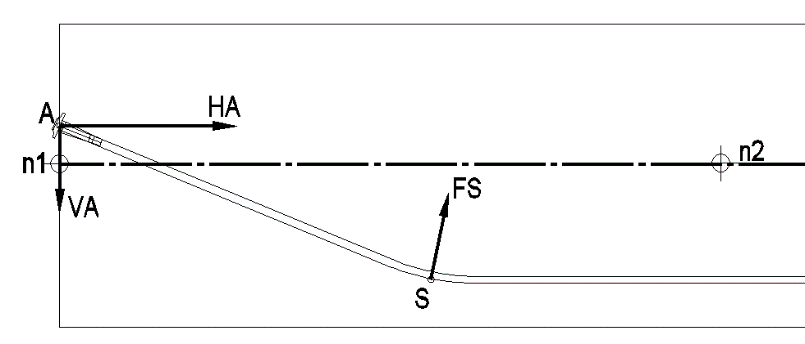
Au niveau de l’ancrage A, le câble applique sur le nœud n1 du modèle le torseur (HA,VA,MA), MA étant le couple produit par HA au nœud 1. A chaque point de déviation, le câble applique la force FS sur la barre n1-n2. On procède ainsi pour toutes les déviations du câble en terminant par l’ancrage d’extrémité.
C.14.3 Modélisation de la précontrainte dans les dalles
L’étude de la précontrainte dans les dalles s’effectue selon le même principe que pour les poutres, mais sur des éléments de coques.
L’utilisation d’un logiciel spécifique est bien sûr souhaitable sinon nécessaire. Il faudra s’assurer que la modélisation des éléments est bien réalisée à leur centre de gravité, et que la somme des réactions d’appui du cas de charge précontrainte est nulle.
C.14.4 Mise en tension des câbles (côté, ordre)
Attention au fait que les efforts apportés par la précontrainte, après pertes par frottement et recul d’ancrage, dépendent fortement du mode de mise en tension (par un seul côté, des deux côtés). Pour des câbles très longs, l’erreur peut s'avérer importante.
De même pour des structures fortement précontraintes, l’ordre de mise en tension peut avoir un impact et il n'est pas inutile de vérifier la structure à certaines phases intermédiaires de mise en tension.
$translationBooksC.15 Compléments liés au calcul phasé
C.15 Compléments liés au calcul phasé
Le lecteur pourra se reporter également à la Partie 1 - D.3 Les phases de construction.
Le phasage structurel peut conduire à la modification :
-
des sections résistantes ;
-
des conditions d’appui ;
-
des conditions de continuité internes de la structure.
Il peut concerner aussi bien les structures en élévation que les structures linéaires, longitudinalement ou transversalement, et bien sûr, la combinaison de tous ces cas est possible.
C.15.1 Comment faire un calcul phasé avec un logiciel non phasé ?
Cas A - Modification de la section résistante
C’est le cas lors de la mise en oeuvre des prédalles collaborantes autoportantes.
Dans la phase de réalisation, c’est la prédalle qui doit résister au poids de la structure (poids prédalle + dalle de compression). Ensuite, c’est le complexe [prédalle + dalle de compression] qui reprendra les charges ultérieurement mises en œuvre (superstructure, surcharges, …).
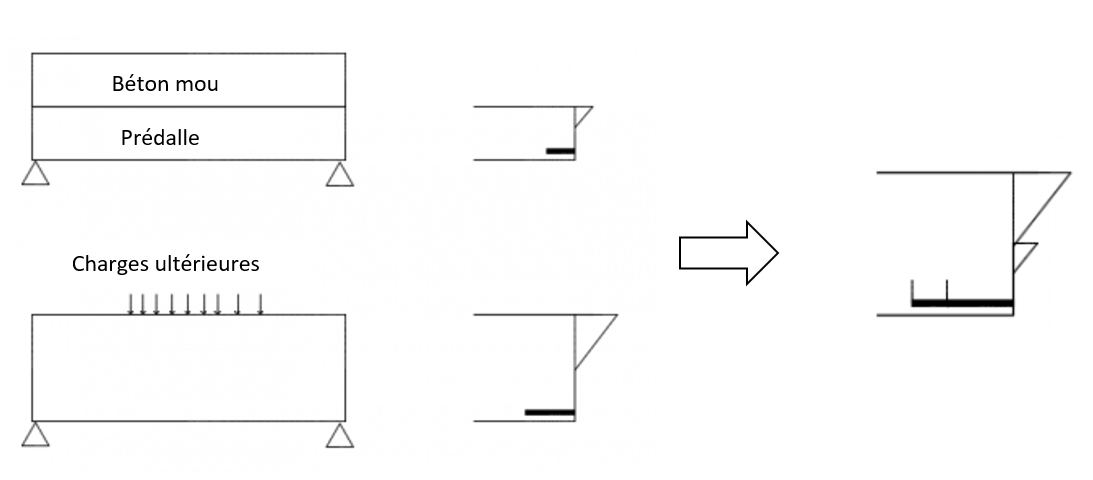
A l’ELS, il y a cumul des contraintes dans l’acier tendu, mais il n’y a pas de cumul direct des contraintes de compression dans le béton.
A l’ELU, la vérification est à réaliser pour la phase de bétonnage et pour la phase de service, mais sans prise en compte du phasage.
Cas B - Modification des conditions d’appui
C’est le cas d’une structure qui présente des appuis provisoires.
Il peut être associé à une modification de la structure résistante (exemple : prédalles collaborantes étayées).
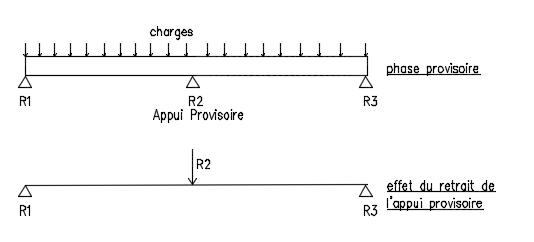
→ Cumul des sollicitations
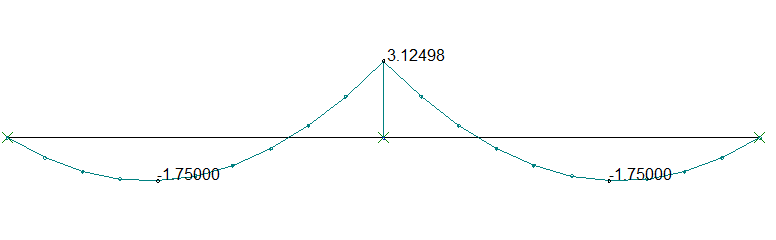
Phase 1 : Chargement sur la structure avec appui provisoire
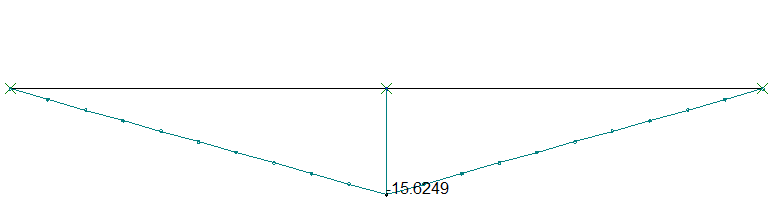
Phase 2 : Retrait de l’appui provisoire
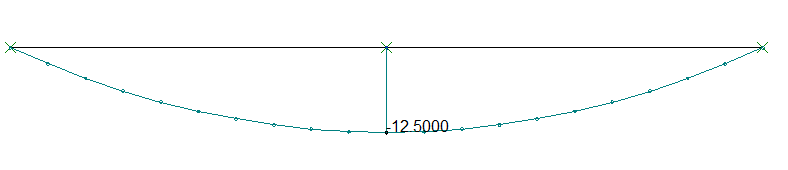
Phase 1 + Phase 2 : On retrouve bien une sollicitation finale identique à une structure non phasée.
Cette méthode permet de traiter la mise en place et le retrait d’appuis provisoires.
Il faut toujours faire attention aux conditions de déformation des structures lors de la mise en place d’appuis provisoires (mise au contact de l’appui provisoire sur une structure déformée)
Cas C - Modification de la continuité structurelle
C’est le cas d’une structure qui est clavée en cours de construction.
On calcule les sollicitations générées par les charges associées à un schéma statique, puis on cumule les sollicitations (s’il n’y a pas eu d’évolution de la section résistante) ou on cumule les contraintes (s’il y a eu évolution de la section résistante).
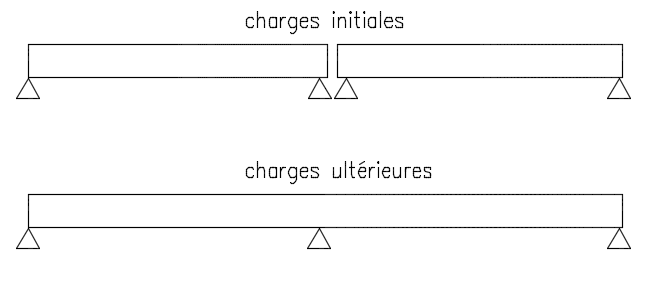
→ Cumul des sollicitations
Exemple :
Phase 1 : Poids propre repris par des travées isostatiques
Phase 2 : Surcharge reprise par une structure continue
Il faut faire attention à l’évolution des matériaux dans le temps. Dans le cas de structures en béton armé ou précontraint ou mixtes béton-acier, il faut prendre en compte le fluage (quantifiable par la différence entre la déformation instantanée et la déformation différée).
Dans l'exemple ci-dessus, avant clavage, la déformation de la structure correspond à une déformation quasi-instantanée. Après clavage, le béton réalise son fluage, tente donc d’augmenter ses déformations sous charge de longue durée, mais la structure est maintenant continue. Le bridages des déformations de fluage va ici générer sur l'appui un moment de continuité qui tend la fibre supérieure.
La prise en compte du fluage peut se faire de manière approchée (voir les documents du CEREMA sur le sujet) ou à l'aide d'un calcul EF avec fluage dit scientifique.
C.15.2 Poussage d’un pont en béton et lançage d’un pont métallique
Les deux modélisations ont en commun le fait que le pont, pendant ses phases de mise en place, va voir la position des nœuds d’appuis varier en fonction de l’avancement du poussage ou du lançage. Potentiellement, tout nœud de la structure peut être, à un moment donné, un nœud d’appui. Les logiciels acceptant un pseudo-langage de programmation peuvent, dans ce cas, présenter un avantage pour créer des boucles incrémentales permettant de simuler l’avancement (par incrémentation des numéros de nœuds d’appui). Dans la mesure du possible, avoir des barres de longueur identique facilite le déplacement régulier des appuis.
La modélisation des avant-becs, dans les deux cas, ne pose pas de problème particulier : ce sont des barres métalliques, généralement des I, encastrés à l’about de la structure définitive.
Pont poussé en béton : Le calcul est un calcul phasé presque classique. Les tronçons coulés sur longrines à l’arrière du pont sont modélisés par des barres reposant sur des appuis resserrés non linéaires en Z (soulèvement possible). Les barres, avec leurs dates de coulage, et la précontrainte, de poussage ou définitive sont activées, au fur et à mesure. In fine, l’avant bec et une partie de la précontrainte sont désactivés.
Charpente métallique lancée : les modèles peuvent représenter de très classiques bi ou multi-poutres mais également des caissons. Les principales différences avec le modèle du pont poussé en béton résident dans le fait :
-
que la structure est très déformable ;
-
qu’en phase provisoire, les tronçons rajoutés (de l’ordre de 30 m de longueur) reposent sur des appuis ponctuels, généralement deux appuis par tronçons, au lieu d’une longrine continue ;
-
que la structure possède une contreflèche, déterminée préalablement par le calcul de la charpente sur ses appuis définitifs. La jonction des tronçons métalliques doit s’effectuer en prenant les dispositions nécessaires pour garantir la continuité des rotations des extrémités des tronçons ; les deux types de modélisations possibles pour la décrire sont détaillées ci-après.
Lors de modélisation, lorsque l’on rajoute un tronçon à l’arrière de la charpente déjà réassemblée, il faut désactiver l’ensemble des barres et les réactiver en ayant rajouté le nouveau tronçon, sans quoi, il n’y a pas de continuité de la rotation au raboutage (figure ci-dessous) et la structure ne serait pas compatible avec le 3e point ci-dessus.

La modélisation peut aussi être réalisée par un phasage classique sous réserve de procéder à une « présentation » préalable des joints, ce qui consiste à trouver le décalage altimétrique des deux appuis 1 et 2 qui permet d’avoir la même rotation et la même altimétrie à chaque extrémité E1 et E2, schématiquement (figures suivantes) :

Translation verticale pour correspondance en Z des lèvres
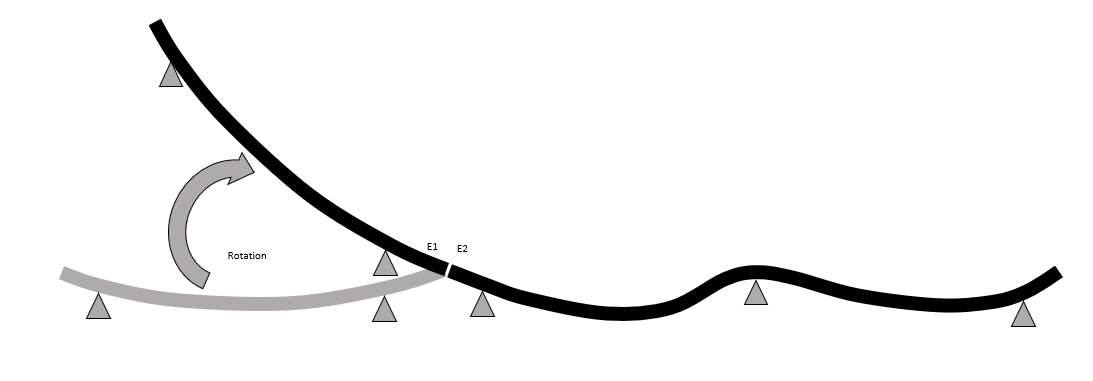
Déplacement des appuis 1 et 2 pour générer une rotation du tronçon
Une fois ces opérations réalisées dans le modèle, la continuité est assurée.
Pour la lançage, une pratique consiste à modéliser les axes neutres de l'ossature et de l'avant-bec suivant une géométrie cumulant algébriquement la forme de l’intrados (rectiligne ou parabolique, par exemple), le profil en long et la contreflèche, à une altitude arbitraire choisie. Au cours de l'avancement de la structure, pendant le lançage, on impose aux nœuds situés au droits des appuis provisoires, une dénivellation correspondant au décalage altimétrique entre la géométrie décrite ci-dessus et l'altitude des appuis provisoires. On vérifiera que la charpente est au contact des appuis de lançage grâce au signe de la réaction d'appui. Un appui en tension signifie que la structure n'est plus au contact et qu'il faut libérer l'appui. Enfin, pour les accostages, il y a toujours deux cas à étudier, juste avant et juste après.
C.15.3 Phasage affectant la section droite des sections
Dès lors que le phasage de construction d’une structure a un impact sur la distribution des contraintes sur les sections droites de la structure, il doit être pris en compte.
C’est le cas des structures construites avec un phasage transversal, où seules certaines parties de la structure voient les premiers chargements : cas des ponts mixtes, à poutrelles enrobées, à nervures avec hourdis coulé dans une deuxième phase, cas des dalles mixtes …
C.15.4 Élargissement d’une structure - Connexions différées
Dans le cas des élargissements, où une structure neuve (métallique ou en béton neuf) est connectée à une structure plus ancienne, la modélisation du phasage transversal et l'appréhension de la raideur relative des différents éléments est indispensable pour déterminer correctement les déformées de la structure et surtout les efforts de couture entre les structures.
Le cas des connexions différées entre plusieurs structures neuves est similaire: la prise en compte du fluage et du retrait s'avère indispensable pour un bon dimensionnement des efforts se développant dans les pièces.
C.15.5 Structure coulée en place ou préfabriquée - Contreflèche - Incidence sur le calcul
On se reportera aux § 2.1 et 2.2 du Guide “Conception des ponts à haubans” du Cerema.
$translationBooksC.16 Compléments liés aux calculs dynamiques et sismiques
C.16 Compléments liés aux calculs dynamiques et sismiques
Les sollicitations dynamiques engendrent des efforts inertiels et cinématiques dans la structure.
Si l'on effectue un dimensionnement suivant l'Eurocode 8, ce dernier fournit une explication détaillée des simplifications admissibles, dans la modélisation et dans le calcul, selon la régularité de la structure. Cette notion de régularité est explicitée au §4.2.3 de l’EN1998-1. Pour les ponts, le guide « Ponts courants en zone sismique » fournit également des critères de régularité et les simplifications de calcul admissibles.
Selon la sophistication du modèle et les objectifs recherchés, plusieurs points de vigilance sont à envisager.
C.16.1 Définition des axes généraux X et Y
La définition des axes généraux X et Y demande une attention particulière, car les résultats sismiques peuvent être erronés si ces axes ne sont pas proches des axes principaux d’inerties de la structure.
Nous indiquons ci-après 2 exemples visualisant ce sujet.
Exemple: Bloc d’angle d’un stade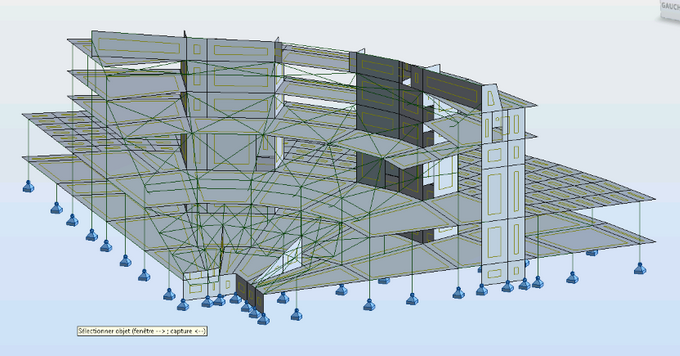
Vue d'ensemble du modèle du bloc d'angle
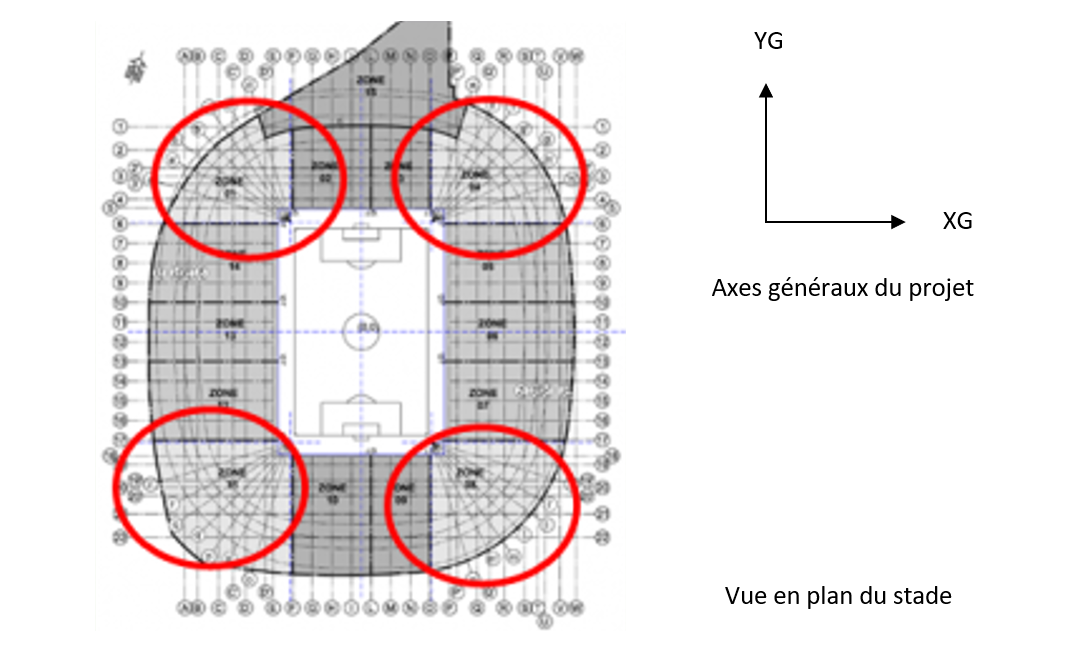
Il est nécessaire d’adopter pour les blocs d’angles des axes de description (X,Y) différents de ceux du projet général (XG,YG). L’axe X doit être radial dans le sens du 1er mode de vibration.
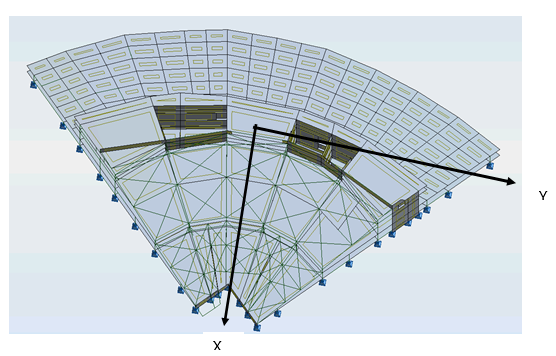
L'étude des modes propres montre alors que l'on retrouve les modes fondamentaux d'un bâtiment classique avec des modes bien différenciés selon les directions X et Y et un mode de torsion ce qui ne serait pas le cas en adoptant les axes généraux XG, YG, car chaque mode entraînerait des masses selon les 2 directions, ce qui perturberait les combinaisons CQC et celles de Newmark.

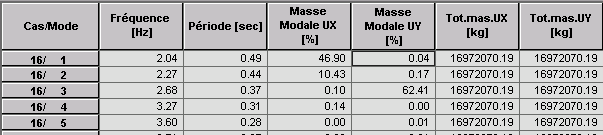
Exemple : Séisme sur un pont courbe
Dans l’exemple ci-après, deux calculs sismiques ont été réalisés pour ce viaduc TGV présentant une courbure en plan.
Le premier selon les axes généraux X et Y orientés selon la culée de gauche et le deuxième avec des axes orientés selon la culée de droite.
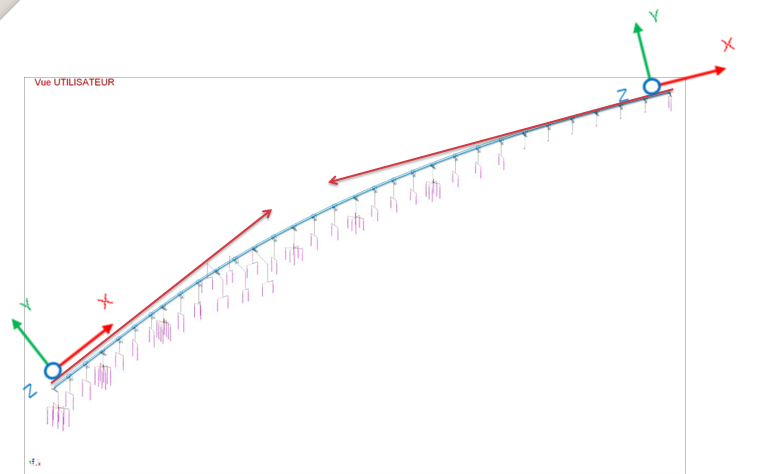
Le passage d’un modèle à un autre est réalisé en modifiant les coordonnées des nœuds du modèle. La comparaison des efforts à la base des appuis met en évidence des résultats très différents entre les 2 modèles.
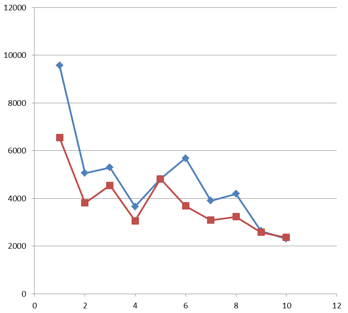
Graphique n° appui/effort en pied (kN)
Il est donc conseillé de réaliser les calculs sismiques des ponts sur des tracés droits en plan si la courbure le permet (se référer aux guides CEREMA), sinon, il faut réaliser plusieurs calculs en faisant varier les axes pour chaque appui étudié, solution complexe à éviter de préférence.
C.16.2 Modélisation des éléments non structuraux ou secondaires
Voir C.4 Modélisation des éléments non structuraux ou des équipements.
Les éléments non structuraux et les équipements n’ont pas à être modélisés si leur masse reste faible par rapport à celle du bâtiment. Cependant, il faut s’assurer que leur raideur n’influence pas le comportement de la structure. Dans le cas contraire, il faut les prendre en compte. Pour un complément d'information, on peut se référer au §2.4.5.2 du guide de l’ASN et au cahier technique 36 de l’AFPS concernant le dimensionnement des éléments non structuraux sous séisme.
La masse de ces éléments non structuraux devra être définie correctement dans l’espace, lorsqu’elle n’est pas négligeable. Par exemple, le décalage des masses des éléments latéraux des ponts par rapport au centre des sections devra être bien défini pour prise en compte dans les modes de torsion.
La répartition des masses sur les planchers peut engendrer de nombreux modes locaux lors d’une analyse modale et rendre difficile l’exploitation du modèle. Il est recommandé, dans ce cas, de privilégier des masses ponctuelles et de refaire une étude locale si besoin.
C.16.3 Transformation des charges en masse
La majorité des logiciels calculent directement le poids de la structure ou possèdent une option pour le faire sur la base de la densité ou du poids volumique des matériaux.
Pour les calculs sismiques et dynamiques, il faut veiller à ce que les poids, forces et pressions soient convertis en masses avec la pondération règlementaire (cas des équipements et superstructures ou d’une partie des charges d’exploitation).
Pour réduire le nombre de modes propres non utiles à un calcul global, on peut privilégier les options qui transforment les masses réparties en masses aux nœuds ou introduire soi-même les masses ajoutées à la main, aux nœuds.
C.16.4 Attention à la cohérence des unités
La justesse des calculs sismiques ou dynamiques est particulièrement sensible à la cohérence des unités. Les forces d’inerties font intervenir l’accélération de la pesanteur g, dont l’unité (généralement définie par défaut) doit être cohérente avec toutes les autres.
Trivial, mais il est toujours utile de rappeler que l'unité de masse est … le kilogramme.
On sera particulièrement vigilant dans le cadre de l’utilisation d’anciennes normes ou règlements, pouvant employer des unités telles que le kgf (kilogramme force). De manière générale, il est conseillé de privilégier l’utilisation stricte des unités système international, a minima pour le contrôle des résultats.
Prenons l’exemple simple du calcul du poids propre. Pour la plupart des logiciels, l’action de la pesanteur est définie par l'application d’une accélération verticale appliquée à l’ensemble de la structure. En interne, le logiciel va calculer la masse de la structure en calculant au préalable pour chaque élément son volume multiplié par la densité de son matériau. Si on désire obtenir le poids propre en N et que les dimensions géométriques et la densité ont été définies respectivement en mm et en kg/mm3, l’accélération devra être définie en… m/s2:
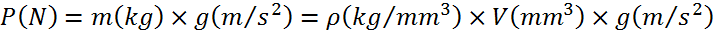
Par exemple la masse équivalente à une surcharge d'exploitation de 20 KN est égale à 20 000 (N)/ 9.81 (m/s2) = 2038 Kg soit 2.038 tonnes.
C.16.5 Matériaux
Les lois des matériaux ainsi que les coefficients partiels dépendent du type d’analyse effectué.
En béton, par exemple, le module d’Young instantané sera privilégié.
Pour tenir compte de l’état de fissuration des éléments, le module EI peut être modifié :
-
soit par un coefficient minorateur appliqué sur le module d’Young E;
-
soit par modification de la section résistante ou de l’inerte directement.
Le référentiel appliqué peut préciser le coefficient de Poisson à appliquer en fonction du type de calcul. Celui-ci pourra être modifié pour tenir compte de l’état de fissuration, par exemple, égal à zéro dans le cas d’un élément fissuré ou sous séisme ELA.
C.16.6 Modélisation des éléments de contreventements des structures métalliques
Les éléments de contreventement assurent la stabilité latérale de la structure. Il est important de traduire leur fonctionnement réel. Par exemple, pour des Croix de Saint-André, les barres ne travaillent qu’en traction, leur mise en compression entraînant leur flambement, instantanément. Les croix ne doivent donc pas être modélisées en totalité si un calcul linéaire est prévu. Dans le cas contraire, on surestimerait la capacité des contreventements avec un facteur de l'ordre de 2. Voir C.2 Modélisation des éléments principaux
C.16.7 Conditions aux limites
Selon les modèles, la prise en compte de l’interaction sol-structure dynamique peut être nécessaire. Il est nécessaire de s’assurer que la structure ne se soulève pas de manière exagérée pour rester dans le domaine de validité d’une étude linéaire si les ressorts sont modélisés de la sorte.
Pour les études sous séisme, l’ingénieur peut calculer les raideurs en se référant aux documents suivants :
-
« Ponts en zone sismique » édité par le CEREMA qui propose au chapitre 4.3.3.2 des formules de calculs assez simples;
-
Conception-construction parasismique - V. Davidovici §4.3.4.4 Modélisation du sol par un système de ressorts amortis - Collection Eurocode - Afnor Editions;
-
Formules de Gazetas : que l’on peut consulter dans l’annexe D de « Fondations et procédés d’amélioration du sol de Davidovici » (ou autres références).
Tous ces documents déterminent les raideurs à partir des modules de cisaillement et des coefficients de Poisson des sols, mais également des dimensions caractéristiques de la fondation. Ces raideurs dépendent des fréquences de vibration de la structure étudiée.
Cas des radiers :
La modélisation d’un radier sous chargement dynamique est plus complexe, car les ressorts devront représenter à la fois les raideurs verticales, horizontales et en rotation, déterminées par l’étude d’interaction sol-structure.
On se référera aux documents spécifiques à ce type d’études.
Plusieurs formes de modélisation sont possibles :
-
par un ressort ponctuel au centre du radier affecté des 6 raideurs (et 6 amortissements), avec des liaisons rigides sur tous les nœuds du radier;
Avantage : une représentation fidèle de l’ISS dans les calculs dynamiques.
Inconvénient : il n’est pas possible de déterminer les efforts dans le radier du fait de la présence des liaisons rigides qui rigidifient artificiellement le radier. Il faut alors procéder à un calcul local du radier soumis aux pressions de sols déduites des efforts dans le ressort central. En particulier, dans le cas d’un radier de grandes dimensions par rapport à son épaisseur, cette méthode n’est pas adaptée.
-
par des ressorts placés uniformément sous le radier (comme pour l’étude statique);
Dans ce cas chaque nœud du radier est relié à 3 ressorts, un dans chaque direction X, Y, Z.
Les ressorts horizontaux selon X ou Y seront déduits directement des raideurs globales en translation, par contre les raideurs des ressorts verticaux devront représenter soit la raideur verticale globale, soit la raideur en rotation globale dans une direction donnée. Cette approche implique 3 modèles de calcul pour analyser les 3 directions de séisme.
Avantage : une modélisation plus simple, permettant de calculer les efforts dans le radier.
Inconvénient : une des 2 raideurs verticales ou en rotation n’est pas représentée dans chacun des modèles de calcul. La raideur en torsion n’est de fait pas intégrée.
-
par la mise en place d’un matelas de ressorts;
Ce type de modélisation est surtout utilisé dans les structures complexes, un matelas de ressorts affectés à chaque nœud du radier permet de représenter toutes les raideurs globales.
Avantage : l’ISS est modélisée finement.
Inconvénient : la modélisation est complexe et ne peut être appliquée qu’en utilisant des logiciels spécifiques en connaissance de cause.
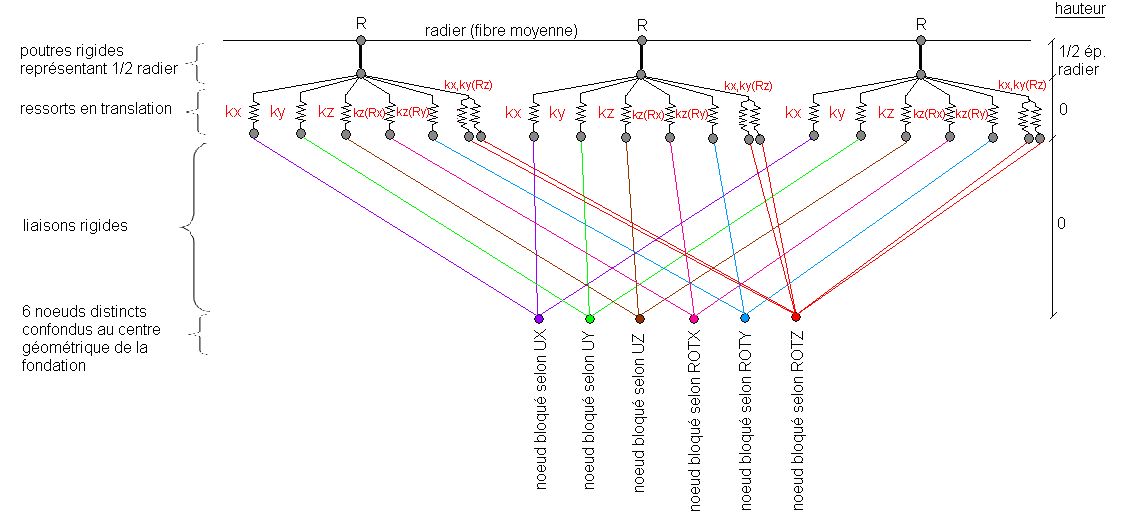
Figure : Schématisation du matelas de ressorts, image Tractebel
C.16.8 Analyse modale spectrale
Troncature – nombre de modes
La notion théorique de troncature est définie dans la partie 1 de ce guide. En pratique, concernant le nombre de modes à retenir pour le calcul, on conseillera :
-
de ne pas dépasser 100 modes pour les ouvrages classiques;
-
d'aller jusqu’à la fréquence de coupure (généralement 33 Hz);
-
de faire appel à un pseudo mode pour la masse participante non prise en compte (EN 1998-2/§4.2.1.2);
-
de ne pas se limiter aux modes ayant le plus de masses participantes, car les modes antisymétriques ont classiquement une masse participante très basse mais induisent des efforts non nuls;
-
de réfléchir à la pertinence de retenir ou non dans l’analyse, les modes locaux.
Coefficients de comportement
Le coefficient ou plutôt les coefficients de comportement, puisqu'ils peuvent être différents dans chaque direction, sont intégrés dans la définition des spectres de calcul. Attention à vérifier que les déplacements calculés sont bien remultipliés par ce même coefficient.
Signature des modes
A l’issue de la combinaison des réponses spectrales, le signe des efforts est perdu (toutes les valeurs sont positives). Ceci peut générer des difficultés d’exploitation lorsque l’on souhaite calculer un torseur ou que l’on souhaite étudier des efforts concomitants (cf. D 7.4.5).
Pour réattribuer un signe aux différentes quantités calculées, il existe plusieurs approches possibles dont celles décrites ci-dessous :
-
Attribution du signe d’un des modes. Pour les structures ayant un mode prépondérant dans chaque direction, il est possible d’assigner le signe du mode prépondérant aux quantités calculées. Ceci est intéressant pour le comportement global de la structure et s’avère très efficace tant que la participation de ce mode est supérieur à 60% de la masse modale de la structure. Par contre, pour les éléments répondant sur des modes locaux plus élevés, ceci peut ne pas être approprié (cf. exemple de planchers épais dans des sites industriels);
-
Attribution du signe suite à une analyse d’accélération uniforme. Pour chaque direction, on applique une accélération unitaire et on retient le signe obtenu;
-
Analyse par la méthode des ellipses. Lorsque la justification d’un élément structurel doit prendre en compte plusieurs composantes de sollicitations, il est loisible d’établir le domaine de concomitance de ces grandeurs, pour ne pas introduire de conservatisme dans le calcul.
C.16.9 Amortissement
Dans le cadre d'une étude de structure avec un spectre de calcul comportant un coefficient de comportement, ce dernier tient déjà compte de l’amortissement. Il ne faut pas vouloir chercher à en rajouter un autre.
Si on est dans le cadre d'un dimensionnement à l'aide d'un spectre de réponse élastique, il faut retenir les amortissements des matériaux.
On veillera dans la mise en données à ce que l’amortissement des matériaux compris ou pris par défaut par le logiciel soient cohérents avec le règlement et l’analyse menée. Par exemple, il est nécessaire de distinguer le béton armé du béton précontraint, ou encore les charpentes soudées des charpentes boulonnées dans la définition des amortissements des matériaux.
C.16.10 Schéma d’intégration en temps et discrétisation
La résolution d’une sollicitation dynamique nécessite la mise en œuvre d’une méthode d’intégration spécifique. Le chapitre 2 de la partie 1 fournit des détails sur ces méthodes et des indications pour choisir le pas de temps et le maillage en fonction du problème à résoudre. Il convient de faire appel à des ingénieurs spécialistes de ce type d’étude.
$translationBooksChapitre D. Analyse et exploitation des résultats
Chapitre D. Analyse et exploitation des résultats
D.1 Généralités sur les calculs numériques
D.3 Exploitation des résultats
D.4 Validations réglementaires : comportement en béton armé des éléments
D.5 Comprendre et analyser les pics (cas du béton)
D.6 Comprendre et analyser les pics (cas d’un assemblage métallique)
D.7 Compléments spécifiques pour les calculs dynamiques
$translationBooksD.1 Généralités sur les calculs numériques
D.1 Généralités sur les calculs numériques
D.1.1 Temps de calcul
Le temps de calcul (au sens large : résolution du système d’équations et stockage des résultats) est un point primordial dans la réflexion à associer à une modélisation aux Eléments Finis.
Il doit rester compatible avec le budget et le délai associés au projet. La recherche d’un temps de calcul optimisé est même un des éléments clés de l’économie d’un projet.
Le temps de calcul est influencé par différents facteurs.
-
Le modèle aux éléments finis :
-
Nombre de degrés de liberté ;
-
Formulation des éléments, nombre de points d’intégration.
-
Des moyens d’optimisation peuvent être l’utilisation de modèles simplifiés, de sous-modèles, de sous-structures, de symétries, de tailles de mailles adaptées localement. Attention toutefois pour les calculs explicites, le pas de temps est calé sur la dimension du plus petit élément.
-
Les moyens informatiques :
-
la mémoire vive (stockage temporaire) ;
-
le système d’exploitation (32 ou 64 bits) ;
-
le calcul est-il fait en local (sur le poste de l’utilisateur) ? sur un serveur local ? sur un serveur externe ? Les temps de copie du modèle et des résultats peuvent s’avérer longs, de même que le temps associé à la liste d’attente des autres calculs lancés sur un même serveur ;
-
la capacité et le nombre de processeurs : on vérifiera le « temps CPU » (Central Processing Unit) généralement fourni par le logiciel.
-
L’optimisation, pour un moyen informatique donné, peut consister à effectuer le calcul en batch (lancement du calcul en lignes de commande sans l’interface), à paralléliser les calculs (sur plusieurs cœurs de processeurs) et/ou à effectuer des poursuites de calcul, si le logiciel le permet.
-
Le type d’analyse :
-
Linéaire/non-linéaire et les algorithmes de résolution associés ;
-
Méthode d’intégration numérique (intégration directe/projection sur base modale, schéma implicite/explicite) et le choix du solveur pour les calculs en dynamique.
-
Le type d’analyse est logiquement associé au problème à résoudre et à la précision souhaitée des résultats ; l’optimisation est donc laissée à la charge du modélisateur. On souligne toutefois que dans le cas d’un calcul transitoire, la durée du calcul (en termes de chargement et réponse de la structure) ne doit pas être surévaluée pour ne pas impliquer de durée de calcul (temps machine) superflue.
-
L’anticipation des « post-traitements » :
-
pour certains logiciels, il est possible de ne sélectionner (et conserver) que les grandeurs d’intérêts choisies par l’utilisateur, de même que les instants (dans le cas de calculs transitoires ou par phases) : le temps machine d’écriture des résultats s’en trouve réduit ;
-
le nombre de modes à sauvegarder/réutiliser dans le cas d’une analyse modale peut généralement être modifié (définition des filtres variables selon les logiciels) ;
-
la visualisation en temps réel des résultats peut permettre de stopper un calcul en cours (mais elle entraîne généralement une augmentation des durées de calcul) ;
-
l’analyse des résultats peut être effectuée à l’aide de post-processeurs indépendants du logiciel de calcul aux Éléments Finis pour réduire les temps d’exploitation.
-
L’automatisation du calcul et des post-traitements (après validation du premier tour de calcul et avec une utilisation réfléchie incluant les vérifications appropriées) s’avère intéressante lorsque l’on considère que l’utilisateur va être amené à réaliser plusieurs fois le même calcul sur différents modèles ou des calculs similaires sur un même modèle.
L’acceptabilité du temps de calcul doit être appréciée en intégrant le fait que le modèle va tourner de nombreuses fois et va se complexifier au fur et à mesure des phases d’étude.
D.1.2 Convergence du logiciel – Cas des calculs élastiques directs
Dans les calculs élastiques directs (calcul statique linéaire et calcul modal spectral), il y a très peu de raisons pour que le logiciel ne converge pas :
-
soit la structure est instable ;
-
soit l’inversion de la matrice de raideur est rendue impossible par des écarts de rigidité trop grands entre les éléments.
Tous les messages d’erreur, à ce stade, sont liés à ces deux cas.
Du fait des conditions aux limites mises en place, certains déplacements, translation(s) et/ou rotation(s) de nœuds de la structure sont imposés (un blocage est un déplacement imposé nul). L’ensemble de ces déplacements bloqués peut cependant apparaître insuffisant pour empêcher un mouvement d’ensemble de la structure.
Il convient, en se plaçant dans un repère approprié, d’analyser les effets de l’ensemble des déplacements imposés sur les mouvements d’ensemble de la structure et d’ajouter éventuellement un ou plusieurs blocages afin d’assurer la stabilité de la structure. On vérifiera à la fin de l’exécution des calculs que les réactions au droit de ces blocages supplémentaires sont nulles ou négligeables ; effort pour un blocage en déplacement, moment pour un blocage en rotation.
Certains logiciels, pour certaines configurations géométriques de structures, passent outre ce problème d’instabilité ; dans ce cas, les contraintes et les déformations sont correctes mais certains déplacements sont quelque peu déraisonnables. Une autre instabilité souvent rencontrée concerne la liaison de types d’éléments structuraux différents est précisée au paragraphe C.6.3.
Il est à noter que les messages d’erreur des logiciels sont parfois peu explicites sur le caractère global, local et/ou numérique des instabilités.
En outre certains logiciels permettent d’aller au bout du calcul malgré un message d’avertissement ou d’erreur. Ceci peut éventuellement aider à comprendre ou visualiser d’où vient le problème, mais on ne saurait se satisfaire des résultats obtenus dans ce cadre.
Il convient, in fine, d’arriver à un modèle qui tourne sans erreurs.
Ces problèmes d’instabilités globales et locales peuvent être détectés en procédant à de simples calculs :
-
soit des calculs statiques linéaires en appliquant une accélération globale (10 m/s2 par exemple) à la structure ; on peut créer trois cas de charges selon les 3 directions principales ;
-
soit à un calcul modal (détermination des premières fréquences propres).
Si la structure présente des instabilités globales, le calcul statique a peu de chances d’aboutir tandis que le calcul modal présentera des modes rigides.
Si la structure présente des discontinuités, ces dernières seront mises en évidence par l’observation de l’allure de la déformée ou des modes propres. Attention, la prise en compte des déformées d'effort tranchant conduit à des ruptures d’allures de déformées.
D.1.3 Convergence du logiciel – Cas des calculs itératifs
Pour les calculs non-linéaires, la convergence d’un calcul aux Eléments Finis est atteinte lors de l’obtention d’une fonction interpolant la solution pour chacun des éléments finis (principe de la discrétisation).
Les critères de convergence sont soit donnés par le calculateur, soit pris par défaut par le logiciel. Le calcul aux éléments finis consiste en une série d’itérations et il s’arrête soit quand le nombre maximum d’itérations prédéfini a été atteint, soit quand certaines mesures d’écart entre deux itérations successives sont inférieures à des seuils prédéfinis (c’est ce qu’on appelle les critères de convergence).
Par contre, ce n’est pas parce que le calcul s’arrête qu’il a convergé vers une solution valide. Par exemple, des critères de déformations trop lâches par rapport à la réalité ou un nombre maximum d’itérations trop faible peuvent fournir un résultat très éloigné de la réalité.
D.1.4 Convergence du modèle
On considère qu’on a atteint la convergence d’un modèle, quand une faible modification de la taille et de la répartition des mailles ne vient pas perturber sensiblement les résultats.
En toute rigueur, il est conseillé d’effectuer une étude de sensibilité du maillage sur les grandeurs post-traitées; ainsi, effectuer la même analyse sur différents maillages (réduction de la taille de maille, par exemple), devrait - si ce n’est fournir des résultats similaires (tolérance à apprécier) - converger vers une solution acceptable par l’utilisateur. On veillera à ne pas raisonner sur les valeurs de pics et à ne pas oublier que plusieurs raffinements successifs de mailles peuvent conduire à une divergence des résultats.
Il convient également d’analyser les messages d’alerte du logiciel (« Warning » sur la taille ou la forme des mailles) pour estimer s’ils sont de nature à altérer les résultats.
$translationBooksD.2 Combinaisons d’actions
D.2 Combinaisons d’actions
D.2.1 Combinaisons et enveloppes
Rappelons qu'utiliser une combinaison d’actions consiste à cumuler les effets structurels de différentes actions, en affectant des coefficients de pondération aux différentes actions, pour correspondre aux combinaisons qui sont définies dans les normes.
En toute rigueur, les règlements demandent de vérifier toutes les combinaisons. Dans le cas d’un bâtiment, le nombre de ces combinaisons reste limité et il est possible pour le logiciel de toutes les calculer. En revanche, dans les cas complexes et notamment dans le cas des charges roulantes, le nombre théorique de combinaisons devient ingérable ; on utilise alors les enveloppes d’efforts.
Une enveloppe est constituée de plusieurs cas de chargement et enregistre uniquement les valeurs extrêmes des différentes composantes (avec les composantes concomitantes).
Conformément aux règlements, certaines actions sur les structures ne sont pas à cumuler, l’occurrence de l’une étant incompatible avec celle de l’autre. Il est alors utile d’intégrer ces actions non cumulables dans une enveloppe, qui va retenir, pour chaque effet étudié, l’action la plus défavorable parmi un groupe d’actions non cumulables. Pour les ponts, on a ainsi classiquement l’enveloppe des actions thermiques, l’enveloppe des actions du vent et l’enveloppe des charges routières.
Rappelons que vouloir cumuler des cas unitaires calculés par une approche non linéaires (NL) n'a pas de sens physique. Certains logiciels autorisent cependant des calculs non linéaires sur des “combinaisons”. Dans ce cas, le logiciel va recréer un cas (la “combinaison”) à partir des cas de charges unitaires et effectuer le calcul NL sur cette somme de charges. Si le logiciel ne le permet pas, il faudra créer des combinaisons en regroupant à la main les charges unitaires. Dans ce cas de figure, il est, encore une fois, fondamental de comprendre ce que fait le logiciel.
Illustration du texte ci-avant sur un exemple
Il s'agit d'une galerie secondaire d'un tunnel. La structure est intégralement appuyée sur des ressorts non linéaires - le sol ne reprenant pas de traction, les ressorts sont neutralisés par le logiciel s'il y a un décollement sol-structure.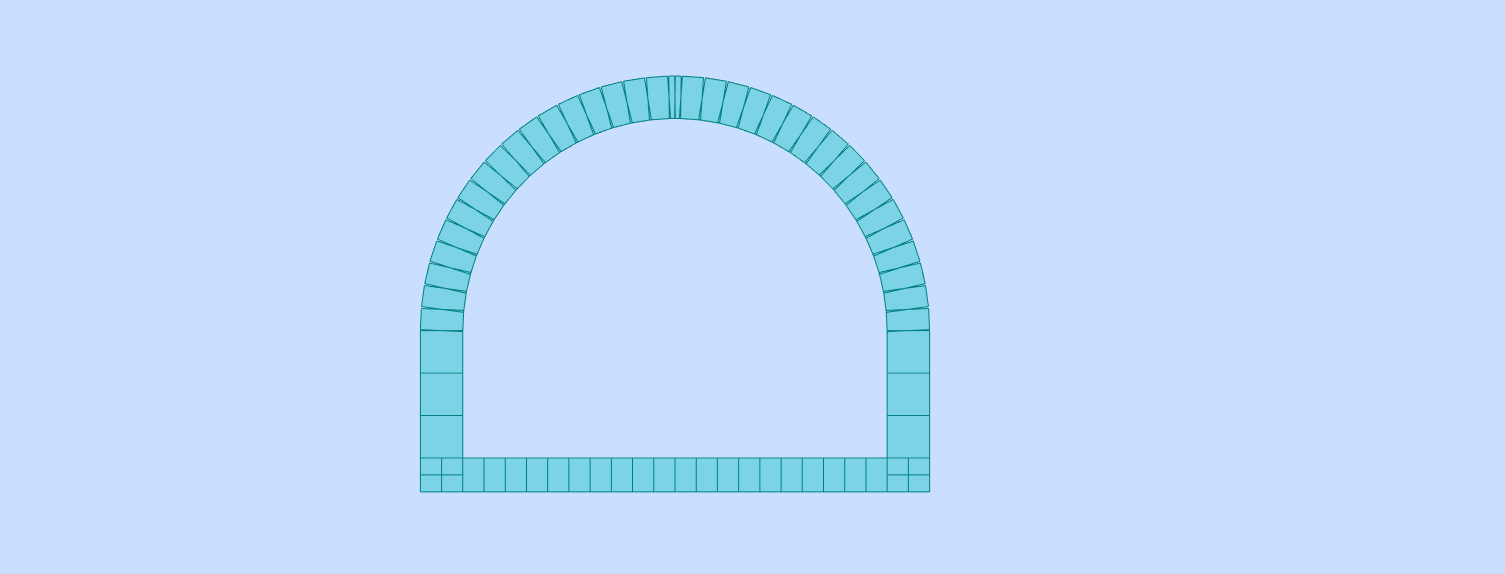
Schéma de la structure
On définit les deux cas unitaires suivants:
-
poids propre + poids et poussée des terres ;
-
sous-pressions hydrostatiques.
Charges gravitaires (à gauche) et charges de sous-pressions d'eau (à droite)
Les résultats suivants montrent que bien que le logiciel soit capable de calculer tous les cas unitaires en non-linéaire, la combinaison des deux cas est recalculée intégralement et indépendamment…
Résultats des cas unitaires: moments de flexion - charges gravitaires (à gauche) et charges de sous-pressions d'eau (à droite)
Résultats de la combinaison des deux cas : moments de flexion - combinaison logiciel (à gauche) et cumul des charges dans un nouveau cas créé manuellement à partir des cas unitaires (à droite) - résultats identiques
… puisque le cumul des cas unitaires n'aboutit pas aux résultats de la combinaison.
Le diagramme des pressions sur le sol est parlant: les sous-pressions d'eau forcent la voûte à s'appuyer sur le sol en partie haute “vers le haut” (figure de droite) …
Pressions sur le sol sous charges gravitaires (à gauche) et sous charges de sous-pression d'eau (à droite)
… mais une fois cumulé au cas des charges gravitaires, le sommet de la voûte ne pousse plus vers le haut, ce que l'on voit sur les résultats de la combinaison faite par le logiciel: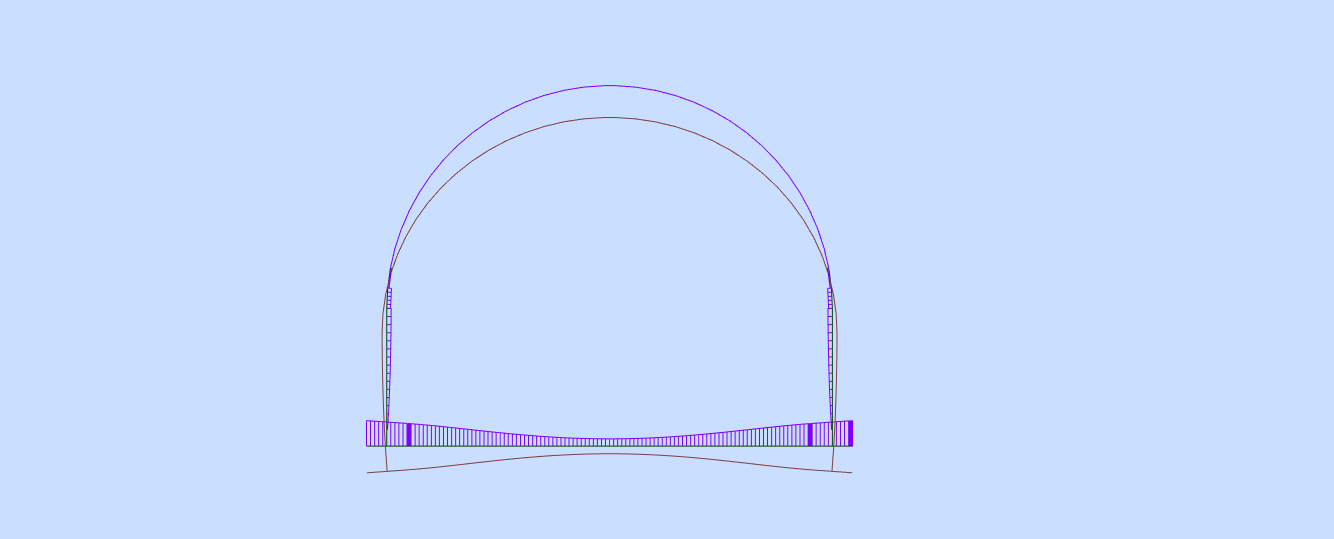
Pressions sur le sol de la combinaison des charges gravitaires et des sous-pressions
Remarque: sans ressorts sur la voûte, le second cas ne convergerait pas.
D.2.2 Attention à l’exploitation des résultats d’enveloppes
L’utilisation des enveloppes entraîne l’enregistrement en base de données des déplacements, des valeurs extrêmes d’efforts, de contraintes ou de réactions d’appui.
La plupart des logiciels de calcul offrent la possibilité de stocker les valeurs extrêmes des efforts et contraintes, soit seules, soit accompagnées des valeurs des efforts et contraintes concomitantes.
Il convient de bien comprendre, avant d’utiliser les résultats des enveloppes pour des post- traitements ultérieurs, si les efforts et contraintes sont ou non concomitants.
Par exemple, si on veut reconstituer l’état de contrainte le plus défavorable d’une section, il convient de vérifier que les contraintes extrêmes que l’on retient pour les fibres supérieure et inférieure sont bien concomitantes.
Penser également à baser l'analyse des résultats, non seulement sur les sollicitations les plus défavorables avec leurs concomitances, mais aussi sur les sollicitations concomitantes qui génèrent les états de contraintes les plus défavorables. Un effort normal maximal associé à un moment concomitant petit peut ainsi générer des effets moins défavorables qu'un effort normal un peu plus petit, mais associé à un moment plus grand.
Pour la vérification d’une section, il est acceptable dans des phases très amont de faire la vérification avec tous les efforts extrêmes dans un même torseur ; mais en phase d’exécution, pour des questions d’optimisation, il convient de récupérer des torseurs d’efforts concomitants.
D.2.3 Attention aux combinaisons automatiques !
L’utilisation des combinaisons d’actions est différente entre le bâtiment et les ouvrages d'art.
Dans le bâtiment, les cas de charges élémentaires induisent de très nombreuses positions possibles qui doivent toutes être explorées pour déterminer les effets maximaux sur chaque élément de structure. Cette multiplicité de charges et de configurations amène très naturellement à l’utilisation de modules de combinaisons automatiques.
De manière générale, l’utilisation des modules de combinaisons automatiques proposés par la plupart des logiciels doit être assortie de précautions particulières car c’est une source fréquente d’erreurs. Certains modules relèvent de la boite noire et tous les logiciels ne permettent pas de savoir directement quels sont les cas de charge élémentaires dimensionnants dans les combinaisons enveloppes.
De plus, la vérification et le codage des combinaisons est un exercice fastidieux et il est difficile de détecter une erreur.
Une des méthodes les plus efficaces pour se prémunir des erreurs liées aux combinaisons et enveloppes consiste à faire l’exercice de décorticage des efforts et contraintes dimensionnants. Il s’agit pour quelques efforts ou contraintes clés de la structure (moment de flexion maximum, contraintes extrêmes) de retrouver la participation de chaque cas de charge élémentaire dimensionnant dans l’effort ou la contrainte globale. On peut ainsi vérifier qu’il n’y a pas d’erreur dans les cumuls et les coefficients et que les cas de charge « logiques » sont bien dimensionnants.
Pour le bâtiment, le même exercice peut être fait sur les réactions d’appui.
$translationBooksD.3 Exploitation des résultats
D.3 Exploitation des résultats
D.3.1 Contraintes/déformations ou efforts internes
L’important est de définir ce que l’on recherche avant de se lancer dans les calculs, et ceci dépend du type d’étude :
-
pour des ouvrages d’art modélisés en poutre simple, on privilégiera l’exploitation des efforts internes ;
-
pour des bâtiments de génie civil, l’approche en contrainte permet d’appréhender le fonctionnement global de la structure en repérant les différentes zones. En revanche, quand l’objectif pour ces bâtiments est d’obtenir des résultats de ferraillage (quantité ou contraintes internes), il est nécessaire d’exploiter les efforts internes et d’effectuer les calculs correspondant dans un second temps.
D.3.2 Valeurs aux nœuds, valeurs aux points de Gauss ou valeurs au centre
Voir également A.2 Qu’est-ce qu’un élément fini ?
Le logiciel calcule les valeurs des contraintes et des déformations en général aux points de Gauss, dont la position est définie dans la notice du logiciel relative aux éléments finis. Il peut en déduire la valeur au centre de l’élément. Il extrapole à chaque nœud et, comme un nœud est forcément lié à plusieurs éléments, il moyenne les valeurs obtenues à partir de chaque élément.
Dans les zones régulières, et avec un maillage adapté au paragraphe C.3 , les valeurs au centre, aux nœuds ou aux points de Gauss sont très proches.
La question se pose à l’approche du pic, où il faut une réflexion sur la valeur la plus représentative.
Type de valeurs affichées
La plupart des logiciels calculent les sollicitations aux points d’intégration (ou points de Gauss). Mais il existe deux façons de les visualiser :
-
soit aux éléments – Cette première façon consiste à tracer directement la valeur moyenne sur chaque élément ; valeur moyenne des valeurs calculées aux points d’intégration de l’élément. Le tracé de la sollicitation présente alors des discontinuités d’autant plus marquées que la discrétisation n’est pas bien adaptée à la zone observée. Les résultats affichés au centre des éléments sont fiables ;
-
soit aux nœuds – Cette seconde façon consiste à afficher les valeurs moyennes aux nœuds. Pour chacun des nœuds, la valeur calculée est la valeur moyenne pondérée des sollicitations issues des éléments sélectionnés adjacents au nœud. Ce traitement, appelé lissage (*), est destiné à afficher un champ continu ce qui peut apparaître plus pertinent.
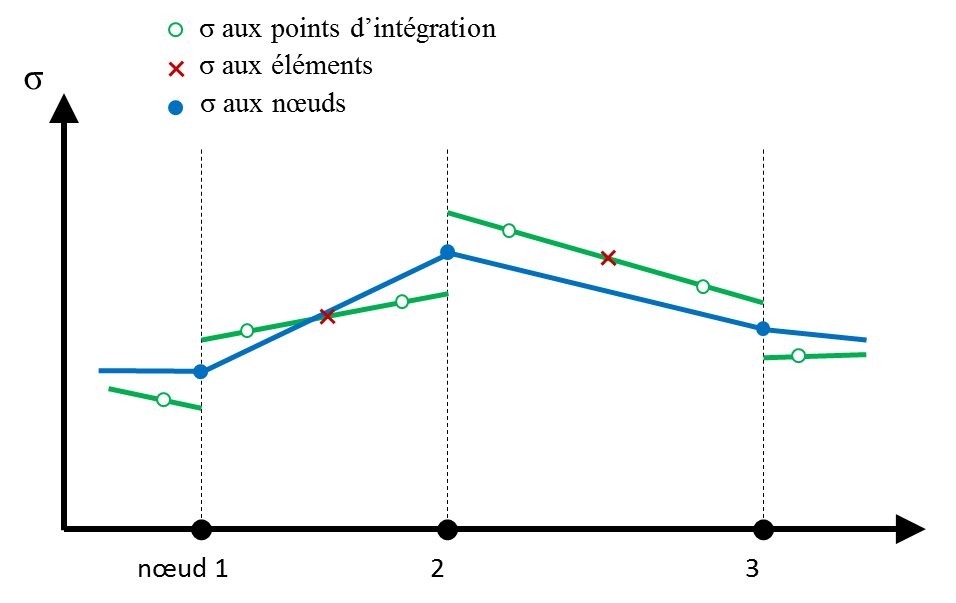
Champ de contraintes – Principe de calcul des valeurs affichées
(*) ne pas confondre cette action de lissage avec les lissages décrits aux paragraphes D.5 et D.6 qui consistent à moyenner des efforts sur une longueur donnée.
Sur la figure ci-après, les sollicitations calculées aux points d’intégration ont été extrapolées aux nœuds avant de procéder à la moyenne. C’est ce qu’effectuent par défaut certains logiciels.
Nous pouvons l'illustrer à partir de l'exemple de la roue Br (Exemple D - Cas simple : modélisation d'une roue Br). Le logiciel utilisé ne donne pas accès aux valeurs aux points de Gauss.
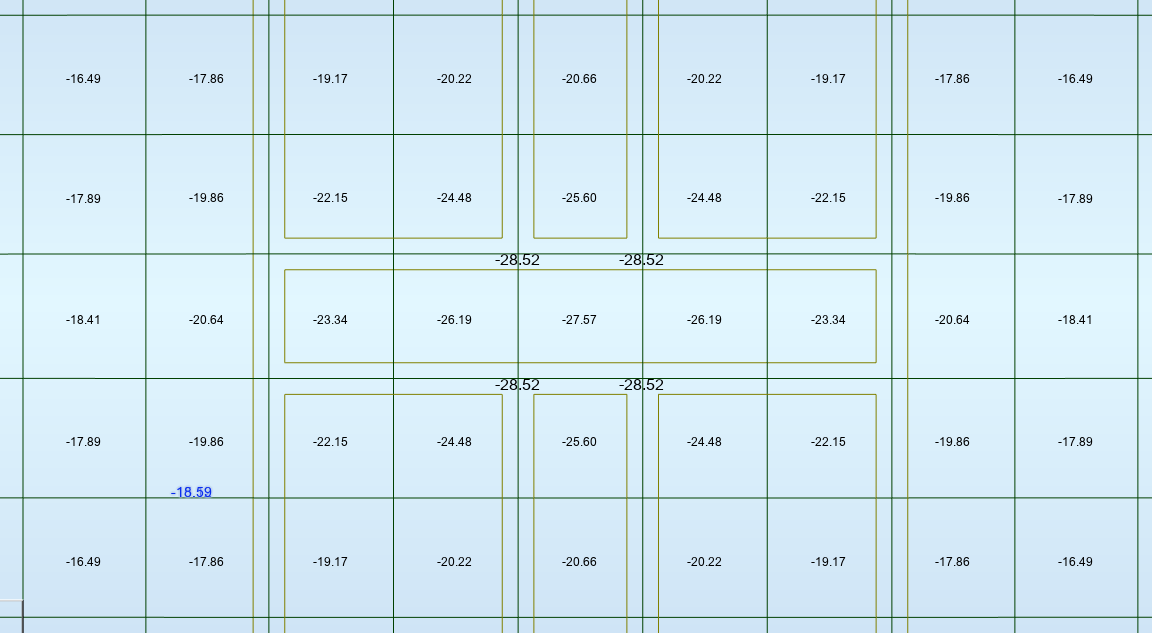
Cartographie des moments transversaux - valeurs au centre des dalles - vue d'ensemble
(28.52 kN.m/m est une valeur extrême du calcul)
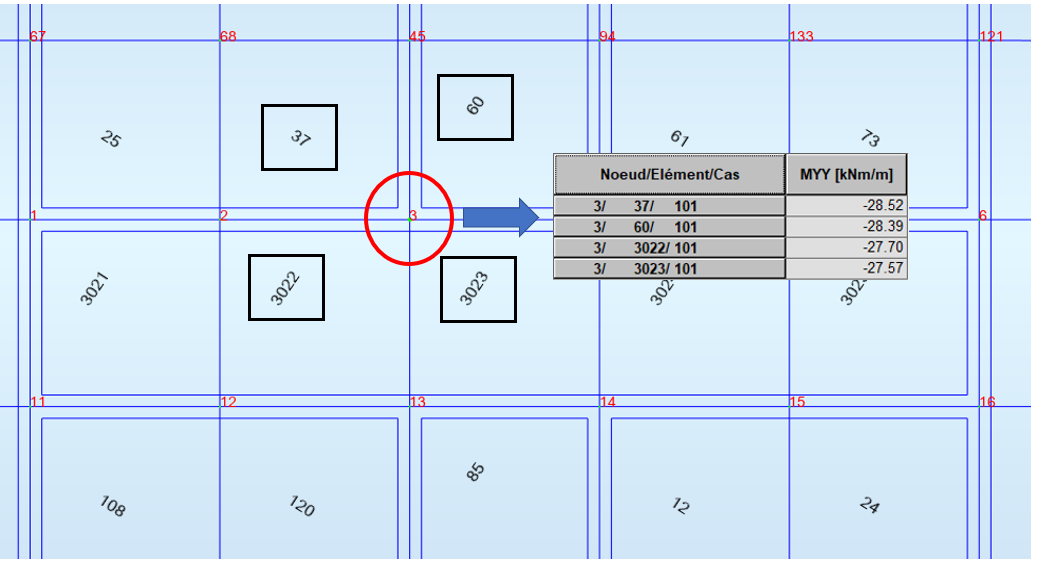
Valeurs au noeud 3 - elles sont différentes suivant l'élément fini de lecture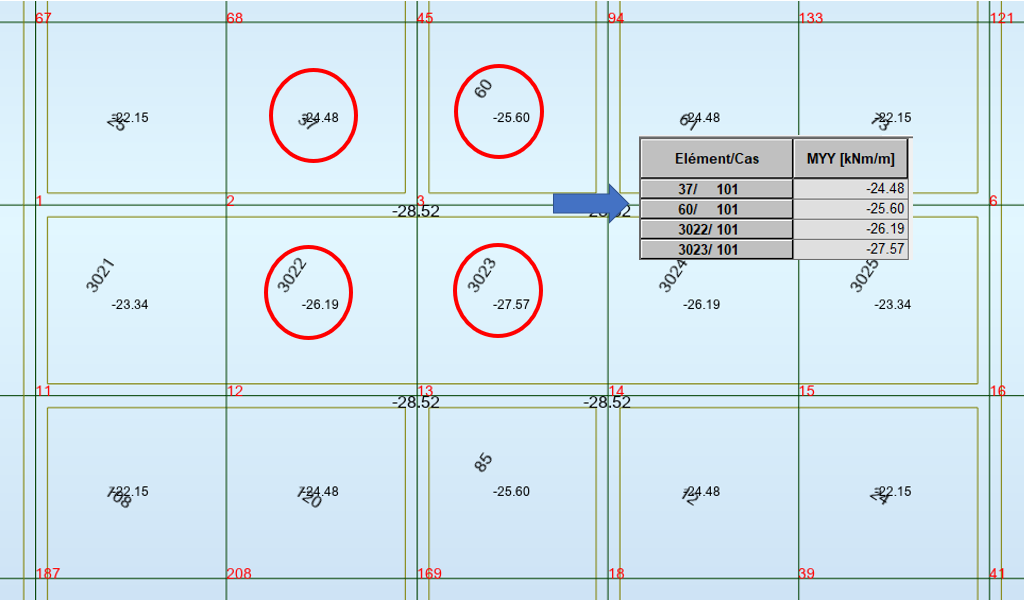
Valeurs au centre des éléments - Zoom
La documentation propre à chaque logiciel doit renseigner sur sa façon de gérer l’affichage des sollicitations et sur les options proposées. Un logiciel peut proposer par défaut que la partie linéaire du résultat du point d’intégration soit extrapolée au nœud alors que la partie non-linéaire (déformation plastique par exemple) soit copiée. Et une option de ce même logiciel peut permettre de copier les parties linéaire et non-linéaire aux nœuds.
On verra plus loin au paragraphe D.5 les variations importantes qui peuvent être liées à des lissages sur les noeuds ou sur les éléments.
D.3.3 Analyse des sollicitations – Repérage des zones sensibles
Pour donner suite aux précisions ci-avant, l’affichage des sollicitations aux éléments permet de mieux visualiser les zones de forte discontinuité. Dans les structures métalliques, on affiche généralement la contrainte équivalente de Von Mises ce qui permet d’avoir une idée des zones fortement sollicitées et/ou présentant un fort gradient de contraintes. On peut également afficher l’énergie interne de déformation de chaque élément. Dans les structures en béton armé, on affiche soit les contraintes, soit les cartographies d’aciers qui permettent de visualiser les zones fortement sollicitées.
$translationBooksD.4 Validations réglementaires : comportement en béton armé des éléments
D.4 Validations réglementaires : comportement en béton armé des éléments
D.4.1 Cartographies d’acier – calcul règlementaire BA / bielles
Les calculs des cartographies d’aciers sont réalisés par les logiciels courants en utilisant généralement la méthode de Capra Maury (Annales de l'ITBTP de décembre 1978) ou la méthode de Wood et Armer (The reinforcement of slabs in accordance with a predetermined field of moments » Concrete février 1968, Aout 1968).
Ces méthodes permettent de déterminer les 4 sections d’aciers Axi, Ayi, Axs, Ays sur les faces inférieures et supérieures d’un élément en fonction des 2 directions de ferraillage considérées orthogonales X et Y.
Une bonne approche du calcul de ces cartographies peut être faite à partir de la méthode de Wood en la simplifiant :
Soit un élément soumis aux composantes d’efforts suivantes :
-
Nxx, Nyy, Nxy efforts de membrane (positif si traction) ;
-
Mxx, Myy, Mxy efforts de flexion.
La première étape est de calculer les efforts intermédiaires suivants :
-
Nwx = Nxx + |Nxy| ;
-
Nwy = Nyy + |Nxy| ;
-
Mwx = Mxx + |Mxy| si Mxx est positif sinon Mwx = Mxx - |Mxy| ;
-
Mwy = Myy+ |Mxy| si Myy est positif sinon Mwy = Myy- |Mxy|.
D.4.2 Éléments en flexion : dalles
Les dalles sont principalement sollicitées par les efforts de flexion Mxx, Myy, Mxy.
Les efforts de membranes Nxx, Nyy, Nxy sont souvent négligeables.
Les moments Mxy peuvent être importants, ils sont nuls dans les zones où les moments principaux sont alignés avec les axes principaux (généralement confondus avec les directions du ferraillage) donc en milieu de travée et sur les appuis continus.
Il ne faut pas les négliger surtout dans les angles des dalles et dans le cas de charges concentrées.
Les calculs des aciers passifs réalisés dans la détermination de cartographies sont conformes aux règles de l’Eurocode, car ils se ramènent à l’étude d’une section rectangulaire soumise à un couple de chargement (N, M), ils peuvent donc être réalisés à l’ELS et à l’ELU.
Le calcul des aciers à l’ELS en prenant en compte les ouvertures des fissures est plus délicat et nécessite l’emploi d’un logiciel éprouvé. En effet, la présence des moments MXY nécessite des calculs d’aciers sur plusieurs facettes car la fissuration ne se produit pas nécessairement selon les directions des ferraillages.
Le comportement des dalles en flexion étant conforme à celui des poutres, il est nécessaire de réaliser un décalage des courbes de moment pour respecter le fonctionnement en treillis.
Les sections d’aciers Ax sont calculées directement à partir du couple d’efforts (Nwx, Mwx) et les armatures Ay à partir de (Nwy, Mwy)
Exemple : Dalle carrée de 5 m de côté
La dalle est articulée sur 3 côtés et encastrée sur le 4ème, elle est soumise à une charge permanente uniforme de 50 kN/m², son épaisseur est de 20 cm, l’enrobage des aciers de 3 cm.

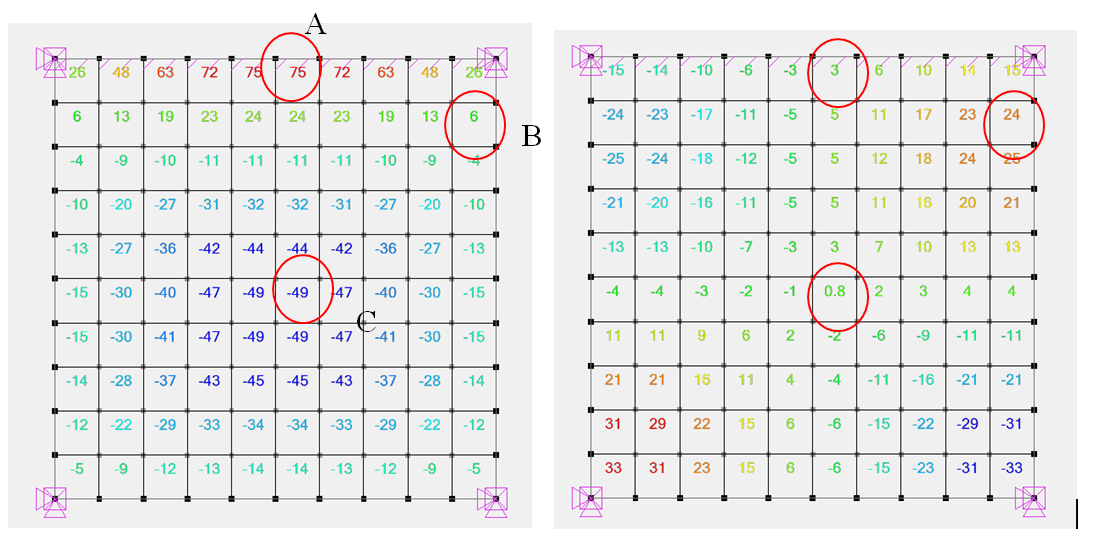
Moments d’axe horizontal MYY | Moments croisés MXY
Les aciers Ay sont calculés manuellement avec fyd=200 MPa (ELS).
| sections : | A | B | C |
| MYY | 75.0 kN.m | 6.0 kN.m | -49.0 kN.m |
| MXY | 3.0 kN.m | 24.0 kN.m | 0.8 kN.m |
| MYY+MXY | 78.0 kN.m | 30.0 kN.m | -49.8 kN.m |
| Ay manuel | 25 cm2 | 10 cm2 | -16 cm2 |
| Ay logiciel | 25 cm2 | 9 cm2 | 17 cm2 |
Ay manuel = 10 x (MYY + MXY)/(0.9 x 0.17 x 200) cm2
Valeurs qui peuvent être comparées avec les sections d’aciers calculées par le logiciel :
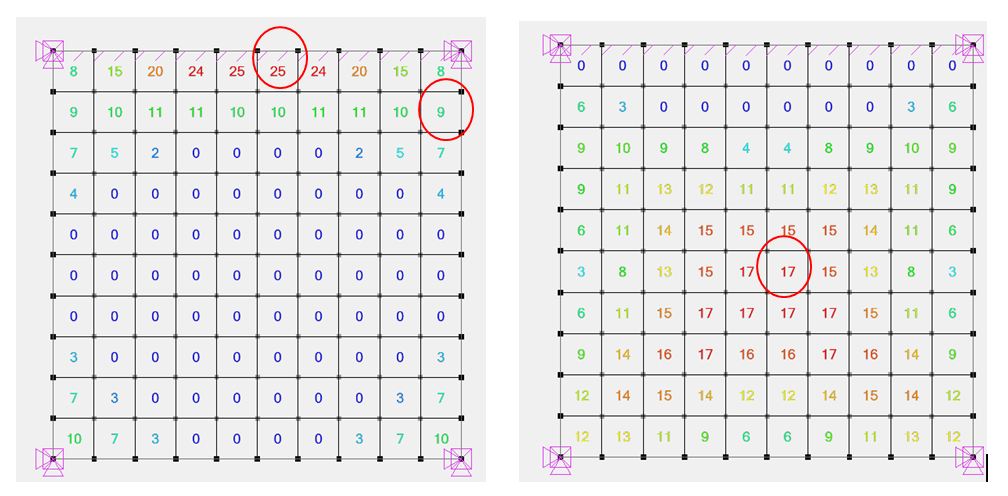
Aciers Ays logiciel / Aciers Ayi logiciel
Il y a une bonne concordance entre les sections d’aciers calculées manuellement et celles déterminées par le logiciel (méthode de CAPRA MAURY).
Il s’en déduit que les moments Mxy se cumulent avec les Moments Mxx et Myy.
D.4.3 Éléments en cisaillement dans leur plan : voiles
Les voiles de contreventement d’un bâtiment sont soumis à des efforts normaux et à des efforts de cisaillements dans leur plan.
Ce sont par exemple les « murs de grandes dimensions en béton peu armé » étudiés dans l’EC8-1 chapitre 5.4.3.5., ou des dalles de transfert de bâtiment soumises à des efforts horizontaux (poteaux inclinés).
Pour ces éléments, les composantes Mxx, Myy, Mxy, Vxz et Vyz sont très faibles voire nulles.
Ils ne sont soumis qu’à des efforts de membrane Nxx, Nyy, Nxy :
-
Nxx et Nyy étant les efforts de traction/compression selon les axes x et y ;
-
Nxy le cisaillement dans le plan du voile.
En reprenant le calcul précédent des cartographies d’aciers, cela donne :
-
Nwx = Nxx + |Nxy| ;
-
Nwy= Nyy + | Nxy|.
D’où les armatures :
-
Ax = (Nxx + |Nxy|)/fyd ;
-
Ay = (Nyy + |Nxy|)/fyd ;
-
Ax et Ay étant la somme des armatures suivant X et Y (2 faces comprises) ;
-
et fyd la contrainte de calcul des aciers.
Ces formules amènent à la constatation que si les efforts normaux sont nuls (Nxx=Nyy=0), alors les armatures Ax et Ay sont des armatures de cisaillements et leurs valeurs sont égales à : Ax= |Nxy|/fyd et Ay= |Nxy|/fyd
Le cisaillement nécessite donc des armatures dans les deux directions, contrairement aux calculs classiques de cisaillement réalisés selon l’EC2. Cela est dû à la non-prise en compte de la résistance du béton.
Les armatures de cisaillements calculées par les cartographies sont donc « supérieures » à celles calculées habituellement en utilisant l’EC2.
On se référera à l’article 5.4.3.5.2 de l’EC8-1 qui concerne l’étude des « murs de grandes dimensions en béton peu armé » qui autorise dans un tel cas de ne pas disposer d’armatures d’effort tranchant si Ved est inférieur à Vrdc.
Il est donc recommandé dans ces cas de n’utiliser les cartographies d’aciers que pour prendre en compte les effets locaux, et de réaliser les calculs des armatures principales en effectuant des coupures à la base des voiles et de déterminer les ferraillages à partir des torseurs résultants au niveau de ces coupures.
Exemple d’un voile :
Etudions un voile isolé de 5 m de hauteur, 4 m de largeur et 20 cm d’épaisseur.
Il est appuyé à sa base, et soumis à une charge horizontale sismique de 2000 kN en tête.
Afin d’éviter les pics d’efforts, la charge horizontale est linéarisée sur la largeur du voile (500 kN/ml).
Voici ci-dessous les efforts de membranes résultants Nxx, Nyy et Nxy.
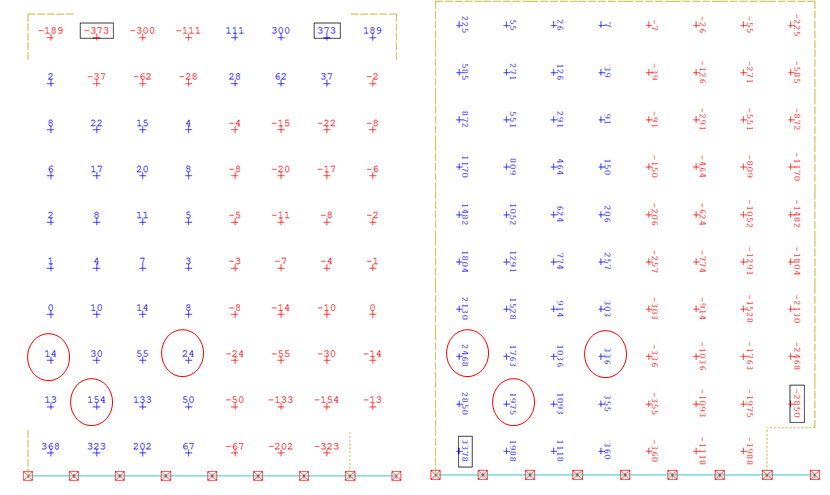
Efforts Nxx (horizontaux)(kN/ml) - Efforts Nyy (verticaux) (kN/ml)
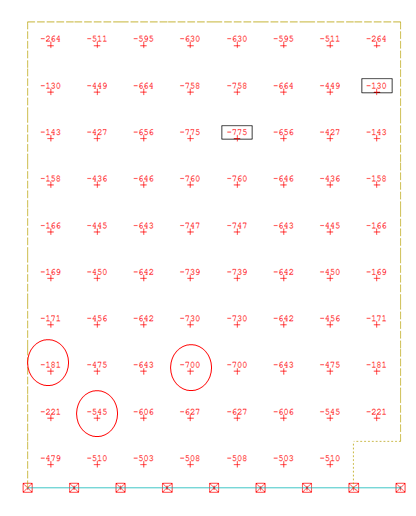
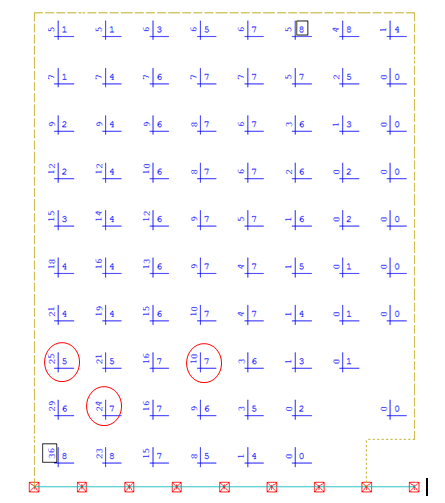
Efforts Nxy (cisaillement) - Cartographies d’aciers (cm²/m²) pour une nappe
Les sections d’aciers sont calculées manuellement et comparées avec les valeurs des cartographies.
| sections : | A | B | C |
| NXX | 14 kN | 154 kN | 24 kN |
| NYY | 2468 kN | 1975 kN | 336 kN |
| NXY | 181 kN | 545 kN | 700 kN |
| NXX+NXY | 195 kN | 699 kN | 724 kN |
| (Axi+Axs) manuel | 4 cm2 | 14 cm2 | 14 cm2 |
| (Axi+Axs) logiciel | 10 cm2 | 14 cm2 | 14 cm2 |
| NYY+NXY | 2649 kN | 2520 kN | 1036 kN |
| (Ayi+Ays) manuel | 53 cm2 | 50 cm2 | 21 cm2 |
| (Ayi+Ays) logiciel | 50 cm2 | 48 cm2 | 20 cm2 |
Ce tableau montre que d’une part le calcul manuel fournit une bonne approximation des sections d’aciers et d’autre part que les efforts de cisaillement Nxy se rajoutent aux deux efforts de membranes Nxx et Nyy, ce qui ne traduit pas la réalité du fonctionnement en béton armé du voile.
Étude réglementaire du voile :
Le voile se recalcule réglementairement selon l’EC2.
Au niveau d’une coupure à la base du voile, les efforts résultants sont égaux à :
-
M-flexion = 2000 x 5 = 10 000 kN.m ;
-
Vu = 2000 kN (ELA).
D’où les aciers de flexion : A-tirant = 10 000 /(0.9 x 3.9 x 50) = 57 cm2 soit 29 cm2 par nappe.

Vrdc = 997 kN est inférieur à Vu = 2000 kN d’où la nécessité de disposer des armatures de cisaillement égales à 11 cm2/ml (soit 6 cm2/ml par nappe) en considérant cot(θ)=1 ou 5 cm2/ml avec cot(θ)=2.5.
Comparaison entre les 2 méthodes :
Les aciers de flexion sont plus importants dans les cartographies car il faut disposer (36+23+15) cm2/ml x 0.5 m= 37 cm2 pour 29 cm2 dans le calcul réglementaire (30% de supplément).
En ce qui concerne les cisaillements , il faut disposer 7 cm2/ml avec les cartographies alors que le calcul réglementaire permet de ne disposer que 2.5 cm2/ml en considérant cot(θ) =2.5.
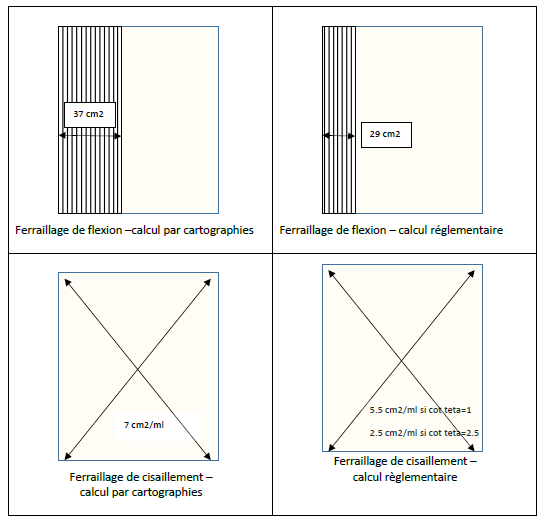
Récapitulatif de la comparaison du calcul d’un voile soit par les cartographies d’aciers soit
par la méthode réglementaire béton armé (EC2)
D.4.4 Méthode des coupures
La majorité des logiciels permettent de réaliser des coupures sur des éléments afin de calculer des torseurs résultants en leurs centres.
Prenons l’exemple de l’étude de la base d’un voile :
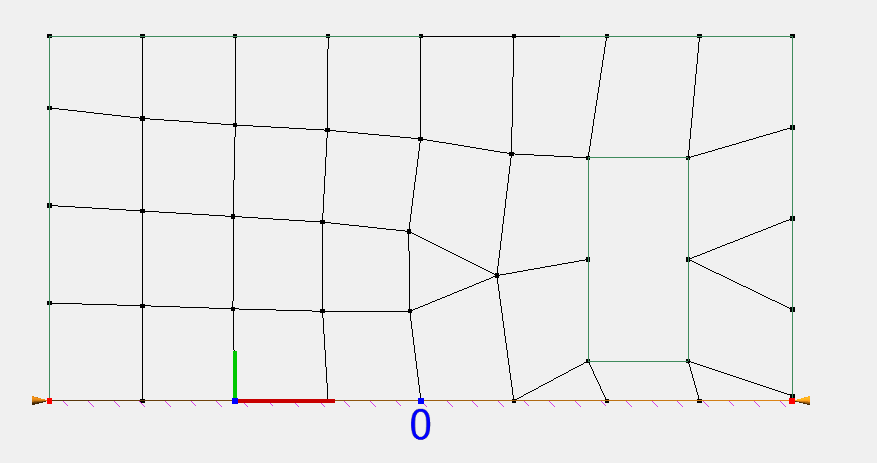
La coupure horizontale au point 0 en base du voile permet d’obtenir le torseur résultant constitué par l’effort normal, le tranchant et le moment (dans le plan ou hors plan), par intégration des contraintes.
Le ferraillage peut alors être déterminé par un calcul type poutre, ce qui implique de s’assurer de rester dans le domaine de définition d’un élément poutre.
L’utilisation des coupures est avant tout très utile à l’ingénieur pour quantifier les cheminements des efforts dans une structure.
D.4.5 Domaine de validité des cartographies d’aciers
D.4.5.1 Cartographies et coupures
Les cartographies d’aciers résultent d’un calcul numérique effectué pour chaque élément indépendamment des autres, donc sans prendre en compte le comportement global en béton armé de la structure.
Nota : La méthode des coupures est la seule respectant le fonctionnement des voiles en béton armé et considérée comme réglementaire. Les compléments usuels sont à appliquer : décalage de la courbe des moments, vérifications des bielles, chaînages et ferraillage minimal … restent à faire.
Il importe donc à l’ingénieur de valider par d’autres méthodes réglementaires les résultats obtenus.
Exemple d’une poutre voile calculé avec la cartographie :
L’exemple d’une poutre sur deux appuis est étudié ici. La poutre est modélisée comme un voile de grande hauteur, pour montrer sur un cas simple les incohérences des cartographies d’aciers.
Soit la poutre isostatique de 10 m de portée, 3 m de hauteur et soumise à une charge uniforme de 200 kN/m2. Cette poutre est modélisée en éléments de plaques travaillant dans leur plan avec un maillage 0.5 x 0.5 m².
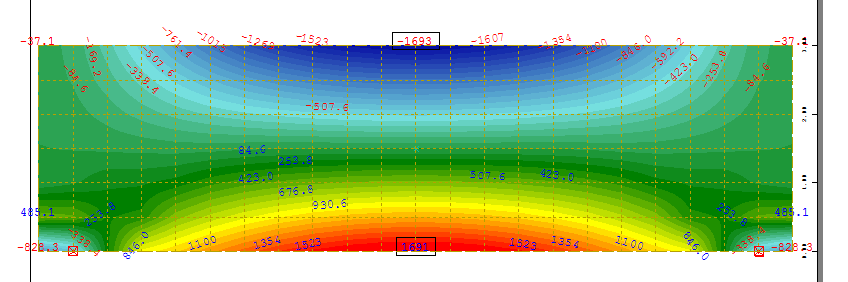
Visualisation des efforts horizontaux Fxx
Calcul du ferraillage à partir des cartographies d’aciers :
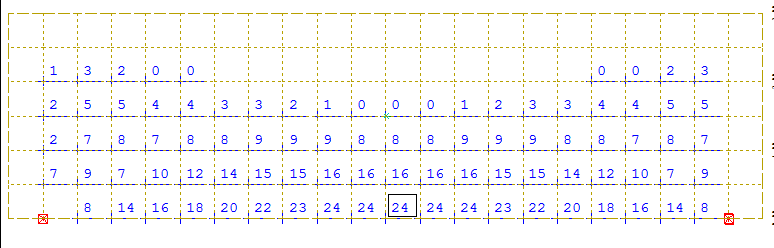
La capacité de flexion est égale à F0 x d0 = 2 nappes x 0.5 m x (24 x 2.75 + 16 x 2.25 + 8 x 1.75) = 116 cm2.m
Le ferraillage à disposer est égal à Ax = 116 cm2.m / 2.9 m = 40 cm2
Calcul du ferraillage à partir des coupures :
Une deuxième méthode consiste à réaliser une coupure au milieu de la poutre (A-A).

Le logiciel intègre les efforts Fxx sur la hauteur de la coupure pour en déduire le torseur résultant au milieu de la coupure.

Le moment au centre est égal à 3358 kN.m, (on retrouve alors le moment classique RDM Mu=1.35ql2/8 = 3375 kN.m), d’où le ferraillage calculé selon les règles du béton armé : A = 3358/(0.9 x 2.9 x 43) = 30 cm2
Conclusion et comparaison des deux méthodes :
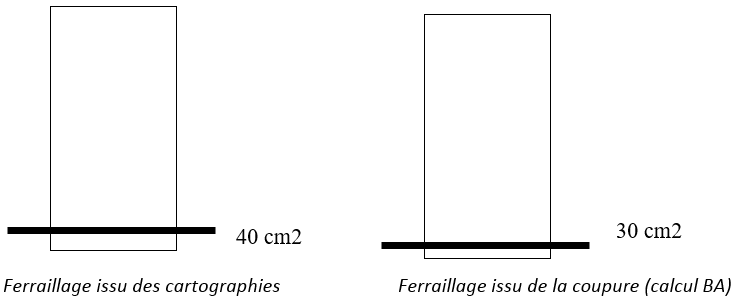
Ferraillage issu des cartographies / Ferraillage issu de la coupure (calcul BA)
Conclusion : Cet exemple montre les limites des cartographies d’acier, car la méthode ne respecte pas la règle des déformations du béton armé. La méthode des coupures permet d'optimiser les ferraillages.
D.4.5.2 Méthode des bielles: apport des éléments finis
Cas d’une poutre-voile (ou poutre cloison)
L’Eurocode 2 encourage fortement l’utilisation de la méthode des bielles, dans ce cas les éléments finis peuvent aider l’ingénieur à définir le schéma de fonctionnement des bielles ainsi que les inclinaisons des bielles. Considérons l’exemple de la poutre-voile suivante :
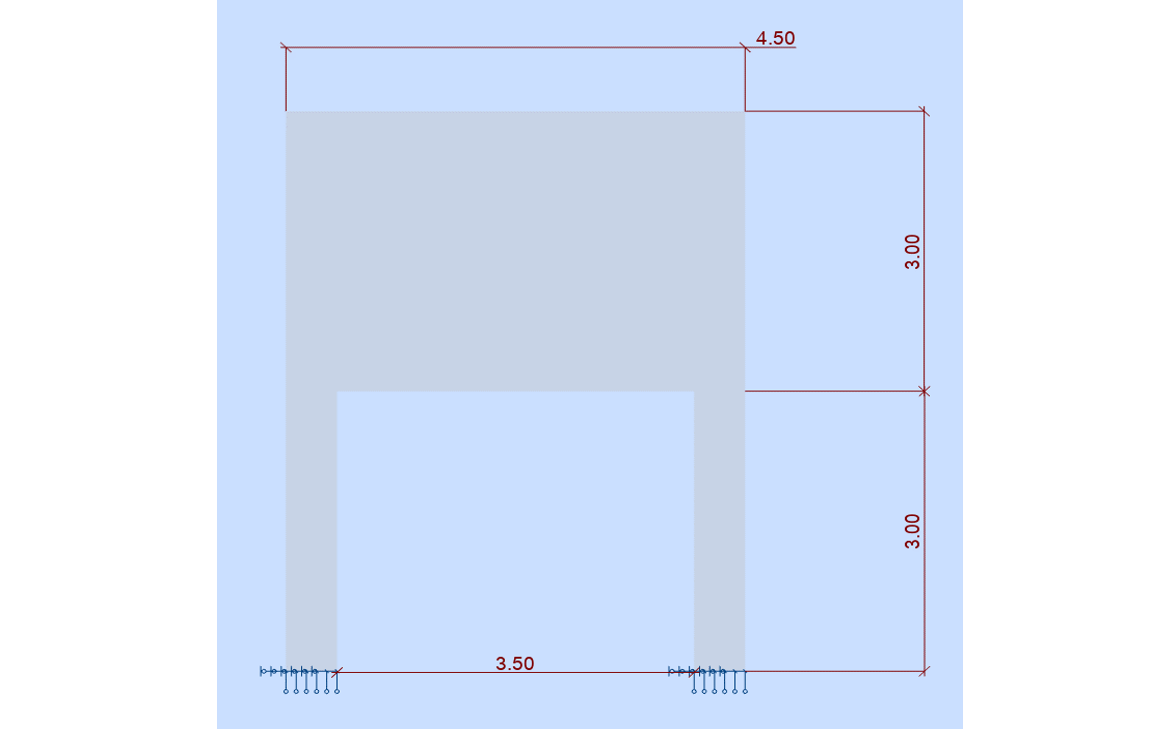
La portée de 3m50 étant inférieure à 3 fois la hauteur de la poutre, les règles classiques des poutres ne s’appliquent pas (EC2-5.3.1), ce voile se calcule par la méthode des bielles.
Cet exemple étant assez simple, nous pouvons définir manuellement le fonctionnement en bielle :
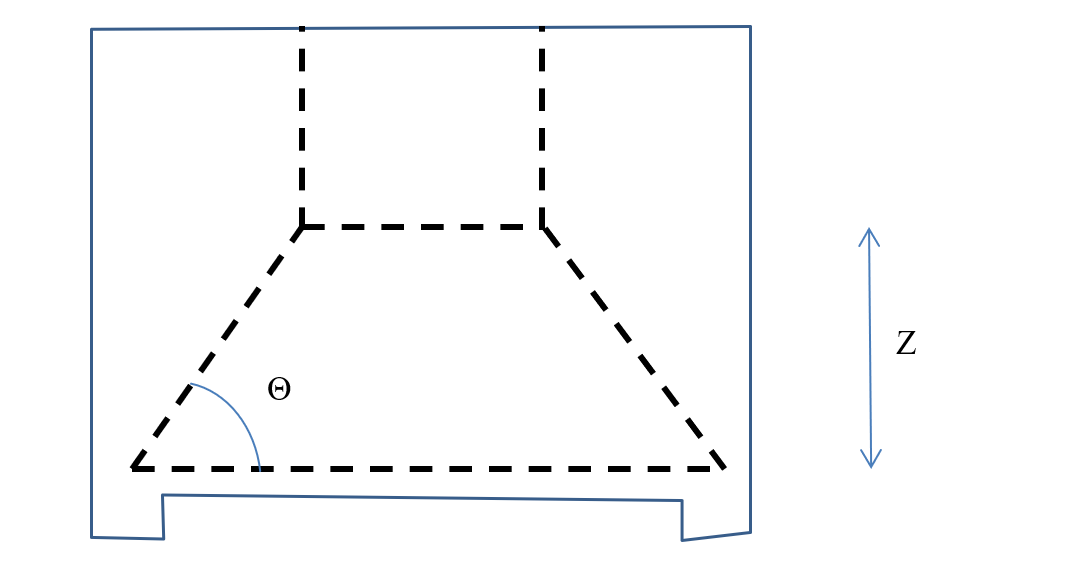
Les règles usuelles estiment la hauteur de la bielle Z à 1.90 m , nous obtenons tgt (Θ) = 2.18, soit un tirant inférieur H=515 KN , soit une section d’acier théorique A=11.8 cm² (calcul ELU).
Dans les cas plus complexes, l’ingénieur devra définir un fonctionnement en bielles qui pourra s’avérer difficile. Les éléments finis apportent alors une aide précieuse pour l’ingénieur, nous proposons à l'ingénieur de suivre la méthode suivante:
Modèle isolé représentatif :
Le principe consiste à réaliser un modèle isolé représentatif du problème.
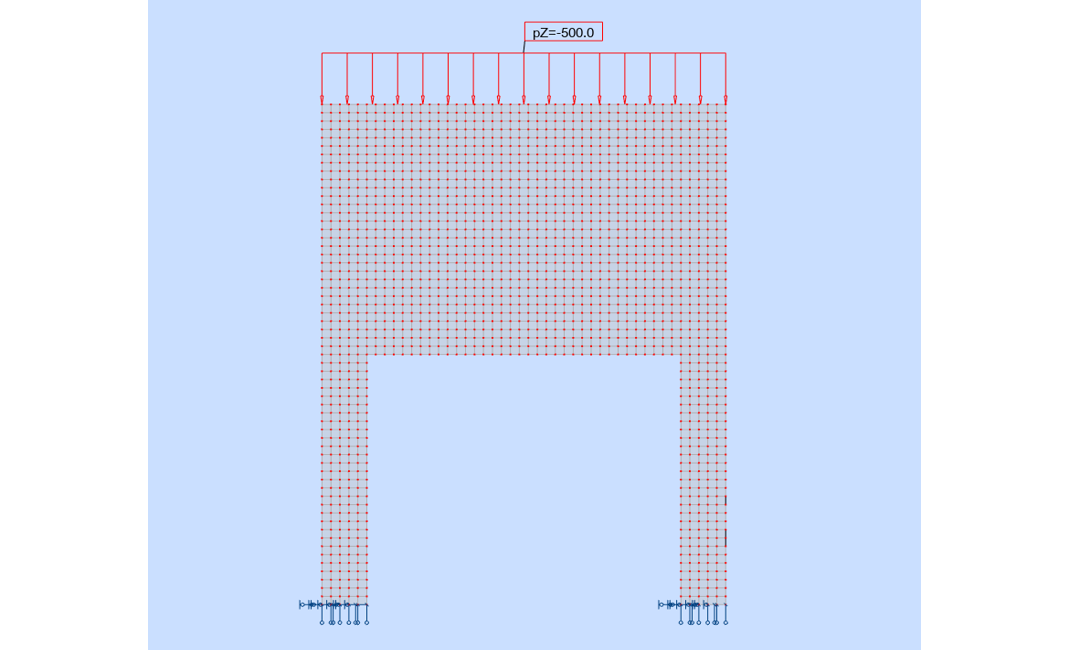
Modèle isolé représentatif
Les contraintes principales :
On se référera aussi à la partie 1 chapitre E.3.3.
Ce qu’il faut retenir : Il y a 2 contraintes principales, la mini S1, la maxi S2, elles sont représentées sous forme de flèches perpendiculaires, la longueur de chaque flèche dépendant de l’intensité de la contrainte. La contrainte S1 visualise les compressions négatives et S2 les tractions positives.
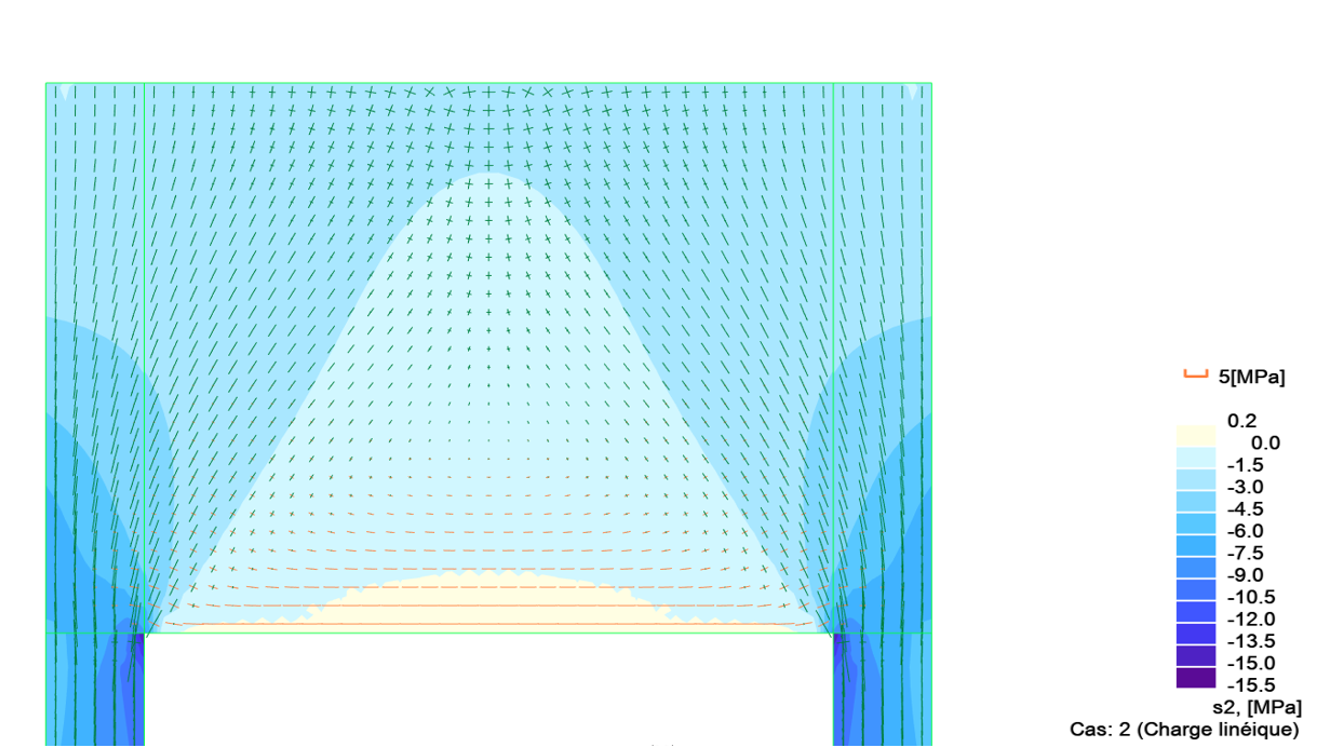
Contraintes principales S2 (compressions)
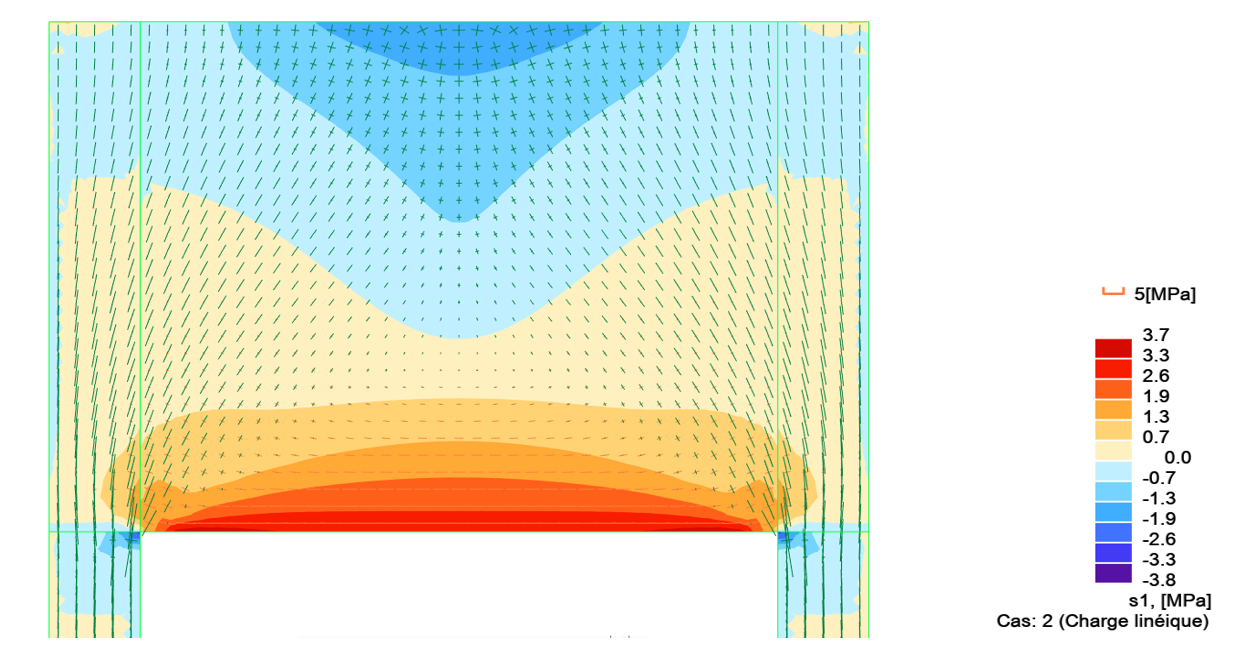
Contraintes principales S1 (tractions)
Dans notre cas, les longues flèches bleues montrent des zones de compression, les rouges montrent les zones de traction.
A savoir aussi : lorsque les 2 flèches S1 et S2 sont quasiment égales, c’est-à-dire lorsque la représentation est une croix, alors la zone est en cisaillement pur.
Définition du fonctionnement en bielles :
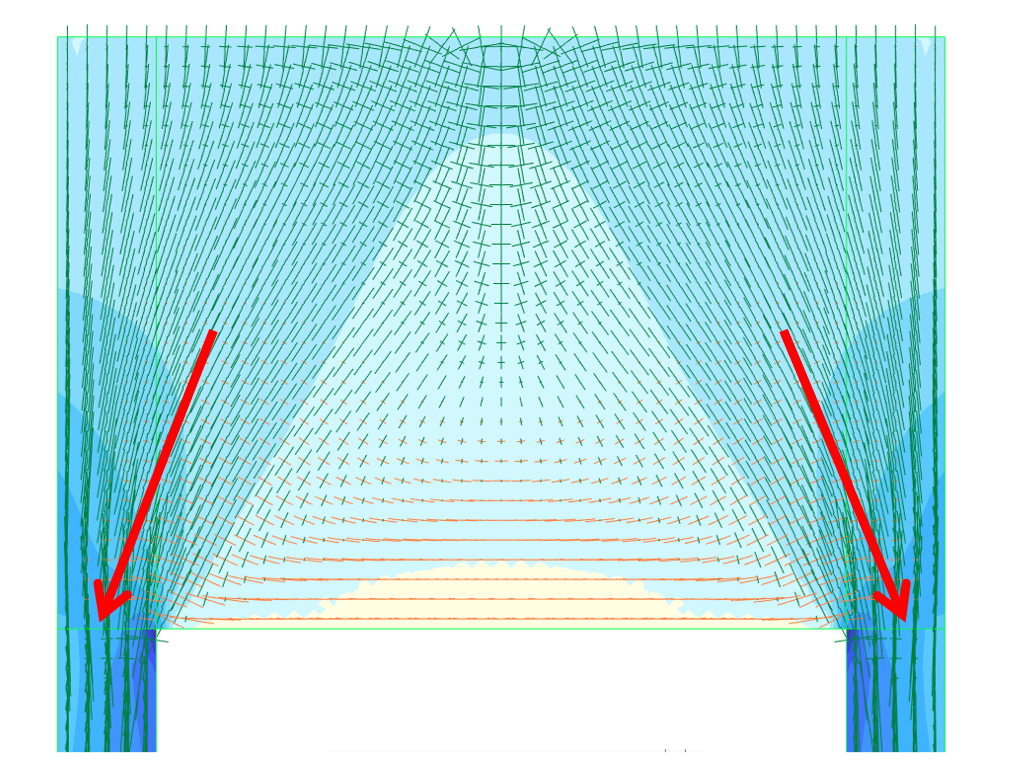
La visualisation des contraintes de compression à la base permet de visualiser la direction de la bielle, sont angle est de l’ordre tgt(Θ)= 2. Soit un tirant de 562 KN d’où une section d’acier A = 13 cm² avec quand même une incertitude due à la méthode graphique.
Cartographies d’aciers :
Les cartographies d’aciers donnent directement le ferraillage du tirant inférieur :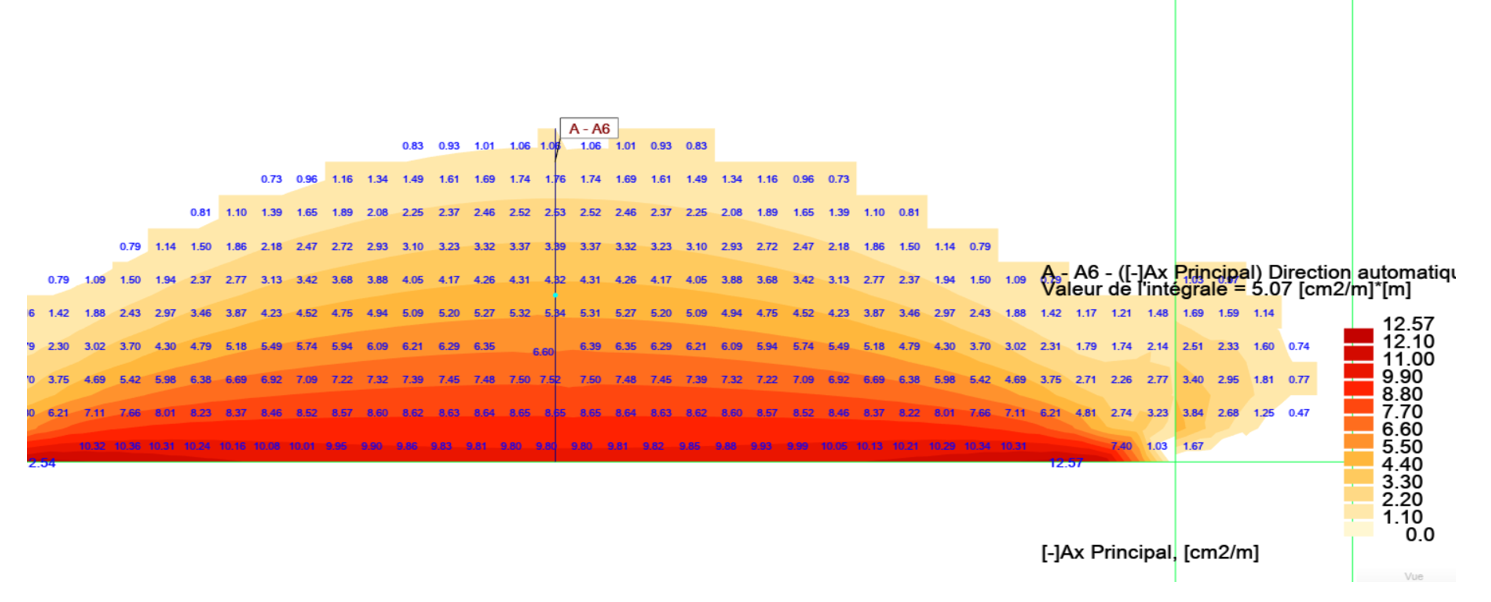
L’intégrale des sections d’acier sur 1 m donne un ferraillage de 5.07 cm² par nappe soit 10 cm² au total. Cette valeur plus précise pourra être retenue.
Bilan
Cette approche permet de bien cerner le cheminement des efforts et de monter un modèle de bielle tirant adéquat (compatible avec le cheminement des efforts).

Cheminement des efforts dans le cas d'ouvertures multiples, contraintes S1

Cheminement des efforts dans le cas d'ouvertures multiples, contraintes S2
Le lecteur se reportera utilement au §8 “Strut-and-tie modelling” du bulletin n°45 de la fib pour obtenir les détails de modélisation de ce genre d'approche et au Bulletin Ouvrage d'Art n°14 du SETRA, pages 23 à 32.
$translationBooksD.5 Comprendre et analyser les pics (cas du béton)
D.5 Comprendre et analyser les pics (cas du béton)
Le lissage dont il est question dans le présent chapitre concerne l'écrêtage d'efforts ou de contraintes ou encore la répartition du ferraillage, en le moyennant, sur une certaine longueur (ou largeur) de l'élément calculé.
D.5.1 Concentration et pic de contraintes (efforts) – différents types de visualisation des efforts
D.5.1.1 Les pics de contraintes et d'efforts
Contrairement aux idées courantes, les pics de contraintes et d’efforts ne sont pas apparus avec les logiciels aux éléments finis, mais ont toujours fait partie des contraintes des ingénieurs structures, ils sont inhérents à la prise en compte d'efforts ponctuels dans le calcul des dalles.
Considérons par exemple l’étude d’une dalle isostatique infinie soumise à une charge concentrée en son centre.
Une approche possible pour calculer les efforts au centre d’une dalle est l’utilisation des abaques de Pücher.
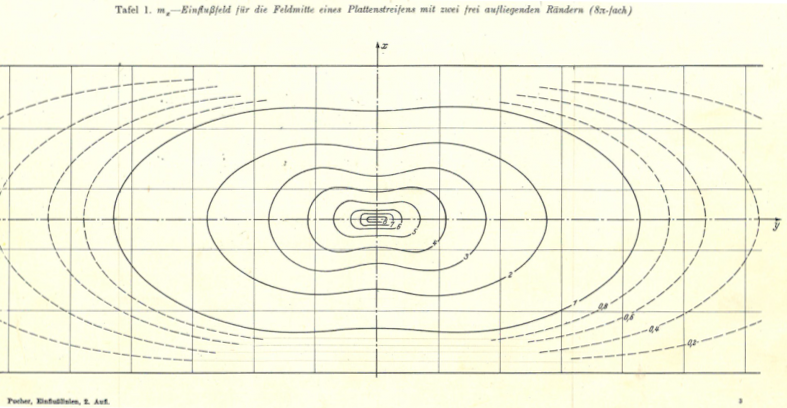
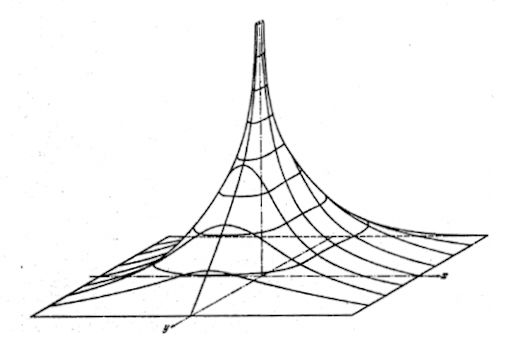
L’abaque ci-dessus (surfaces d’influence) fait apparaître un pic de moments au centre: la ligne d’influence croît rapidement lorsque la charge se rapproche du milieu de la travée : les valeurs 3 / 4 / 5 puis 6 et 7 se resserrent pour aboutir à une valeur infinie, mais correspondant à une surface tendant vers 0. Pücher a arbitrairement tronqué la représentation à la valeur de 8.
Considérons une dalle de 3 m de portée articulée sur ses côtés , soumise à une charge concentrée de 10 KN en son centre.
D'après l'abaque le moment théorique au droit de la charge est infini, ce qui n'est pas satisfaisant pour l'ingénieur devant dimensionner le ferraillage. En réalité les charges ponctuelles n’existent pas, d’autant plus que la pratique courante consiste à diffuser les charges au feuillet d’une dalle. On est alors amené à calculer des intégrales pour obtenir la valeur du moment dans la dalle (pour plus de détails, on se référera aux publications originales de Pücher).
En répartissant la charge sur un carré 20×20 cm², l'intégration des surfaces montre que le moment maximal est égal à 3.0 KN.m.
Un autre exemple de l'utilisation des abaques de Pücher est donné dans l'exemple de modélisation d'une roue Br.
Il ne faut pas oublier que les calculs sont généralement menés avec des sections brutes (coffrage) et des matériaux élastiques (comportement linéaire). En réalité, la fissuration du béton armé va conduire à une redistribution des efforts qui tend à faire diminuer ces effets de pics. Ce genre de calculs n’entrent pas (à ce jour) dans la pratique courante.
Il est par conséquent nécessaire de savoir corriger simplement, souvent manuellement, les résultats d’un calcul linéaire.
Des exemples de correction des résultats d’un calcul linéaire sont donnés ci-après.
D.5.1.2 Étude des pics par les éléments finis
Que se passe-t-il lorsque l'on calcule cette même dalle par les éléments finis ?
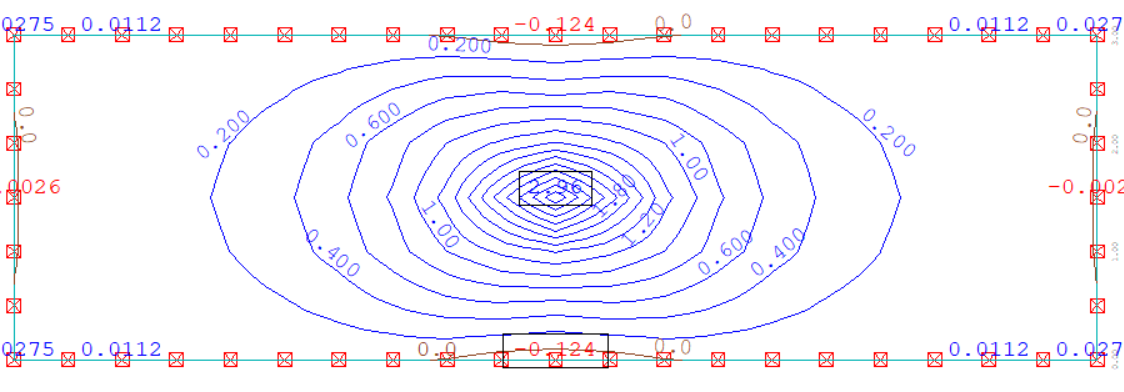
Dalle de 3 m de portée articulée soumise à une charge concentrée de 10 KN en son centre (efforts aux nœuds)
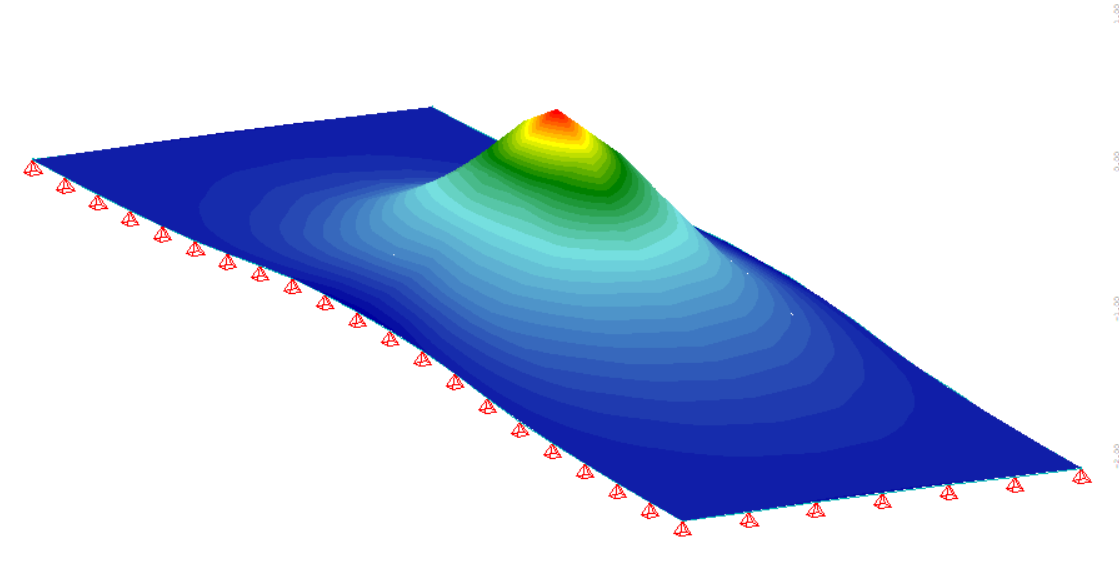 Idem en 3D
Idem en 3D
Nous constatons l’apparition d'un pic dont la valeur maximale n'est pas infinie, mais égale à 2.96 KN.m.
Nous avons vu que le logiciel calcule les efforts aux points d'intégration des éléments, pour extrapoler ensuite les résultats au centre puis sur les nœuds des éléments. un nœud étant généralement commun à 4 éléments, il y a donc 4 résultats par nœud (un pour chaque élément). Quel sera le résultat retenu ? La valeur maximale ? La valeur moyenne ? Les logiciels aux éléments finis ne proposent pas, en effet, un seul résultat pour chaque calcul, mais plusieurs selon les options choisies par l'ingénieur: ils sont capables de dresser des cartographies de résultats à partir des efforts sur les nœuds, ou bien à partir des efforts au centre des éléments, ils peuvent être lissés, non lissés, etc.
L'ingénieur doit choisir les options de visualisations avec rigueur, car les résultats varient grandement selon l'option choisie. C'est ce que nous proposons de montrer avec l'exemple ci après.
La figure précédente visualise les moments calculés sur les nœuds des éléments dont la valeur maximale est de 2.96 KN.m, elle est très proche de la valeur de 3.0 KN.m calculée manuellement.
Nous reprenons le même exemple en affichant les moments calculés au centre des éléments (au lieu des nœuds) ; le pic central est plus petit : 1.92 KN.m pour 2.96 KN.m précédemment. Ce résultat est également éloigné de la valeur calculée manuellement de 3.0 KN.m.
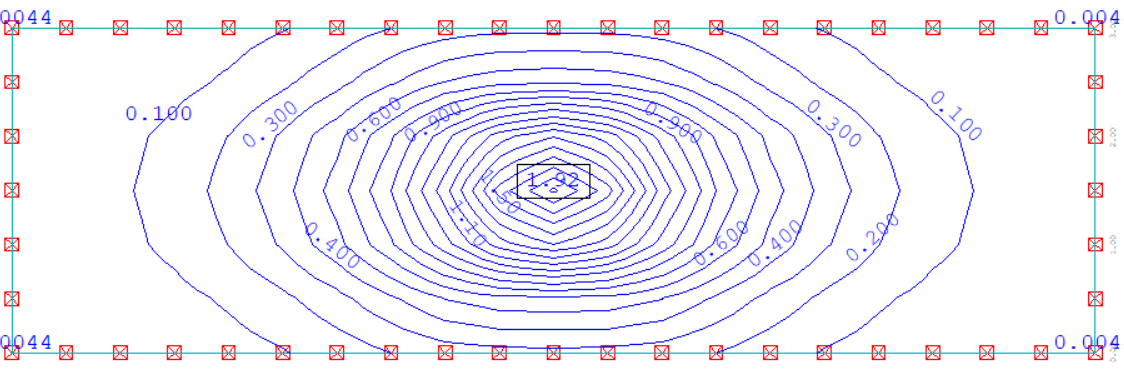
Dalle de 3 m de portée articulée soumise à une charge concentrée de 10 KN répartie sur 20×20 cm² en son centre (efforts au centre des éléments)
La représentation ci après de la courbe des moments sur une coupe au milieu de la dalle permet de comprendre ces différences.
a) Efforts aux nœuds
Ci-dessous la courbe des moments Myy calculés par lissage sur les nœuds
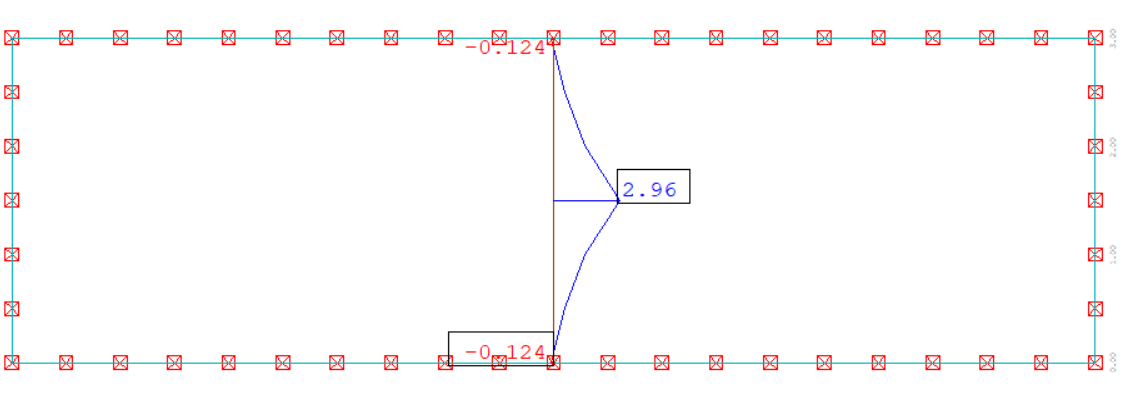
Les efforts sont calculés dans les points d’intégration des éléments puis extrapolés sur les nœuds.
Le moment maximal est de 2.96 KN.m au centre de la dalle conforme au calcul manuel.
b) Efforts non lissés sur les éléments
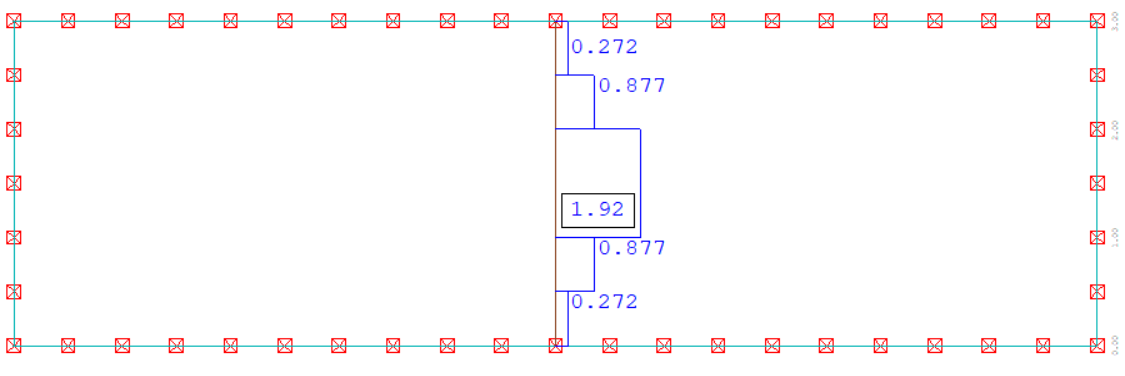
Les efforts sont calculés dans les points d’intégration puis moyennés pour obtenir l’effort au centre de l’élément.
La valeur maximale est de 1.92 kN.m , moyenne des éléments centraux.
On ne retrouve pas ici la valeur calculée manuellement de 3.0 kN.m, mais une valeur « lissée » sur les éléments entourant le pic. Nous retiendrons de cet exemple que les efforts aux nœuds donnent des résultats conformes à ceux calculés manuellement, ce qui n'est pas le cas des efforts calculés au centre des éléments.
c) Efforts lissés sur les éléments
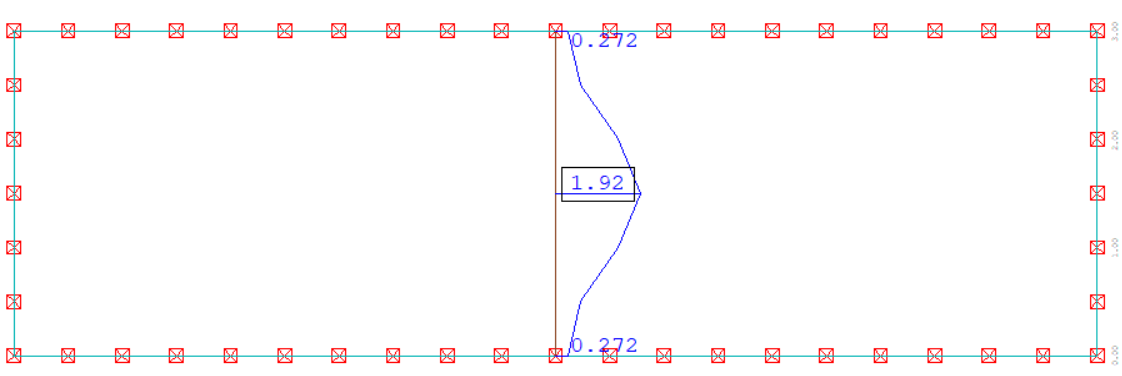
Les efforts sont calculés au centre des éléments puis lissés entre eux.
Cette courbe fait croire à une courbe extrapolée sur les nœuds, alors que les extrapolations sont effectuées seulement sur les résultats aux centres des éléments, la courbe qui en résulte est sans signification physique donc « fausse ».
En revanche, dans un autre cas de figure, cette option de lissage des efforts au centre pourrait s’avérer utile si l'on désirait connaître les efforts aux nus de voiles.
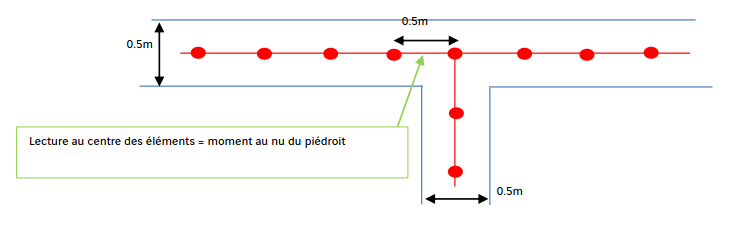
Pour être valable, la largeur de la maille devrait être égale à l’épaisseur du voile.
Les visualisations des résultats des éléments finis au droit des pics donnent des résultats très différents selon les options choisies par l'ingénieur. Ces résultats ne peuvent pas être pris tels quels, mais doivent être analysés et interprétés par l'ingénieur.
La figure ci-dessous montre les valeurs obtenues avec une force ponctuelle de 10 kN au centre de la dalle.
La valeur de moment passe à 5.2 kN.m et l'allure de la courbe de moment présente nettement un pic.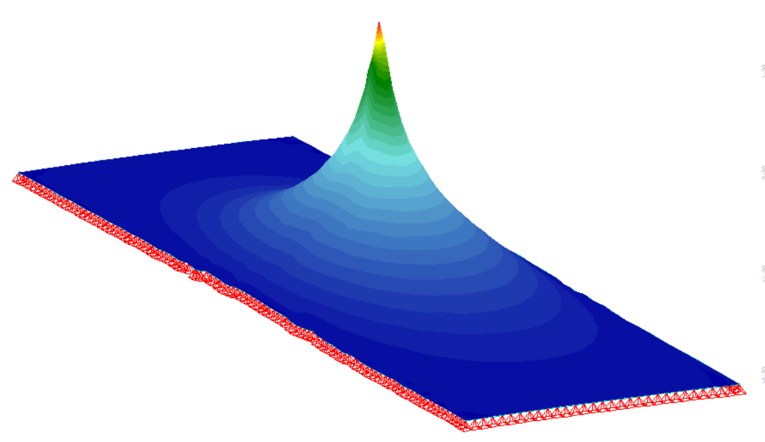
Plus loin dans le présent chapitre, on verra que les forces ponctuelles (qui n'ont pas de sens physique) conduisent à des pics d'efforts et qu'il vaut mieux éviter leur emploi pour obtenir des résultats locaux précis.
D.5.2 Méthode d’analyses des pics
Les cartographies d’aciers présentent souvent des pics d’aciers dont les conséquences sont très importantes dans le dimensionnement du ferraillage.
L’utilisateur est souvent dépourvu devant ces pics : faut il les prendre en compte en considérant qu’ils sont structurels ou les ignorer en les assimilant à des problèmes de calculs numériques ?
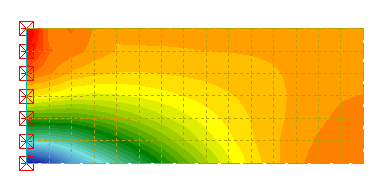
Exemple : les pics visualisés ci-dessus à l’encastrement de cette poutre en console sont bien entendu structurels.
La réponse à cette problématique réside dans la compréhension du fonctionnement de la structure et du cheminement des efforts au niveau du pic, analyse indispensable pour solutionner les pics (écrêter, linéariser les ferraillages).
Cette démarche peut s’avérer difficile dans le cas de modélisations complexes, mais est toujours indispensable.
Trois types d’analyses sont envisageables :
| Analyses | Objectif |
| 1 : Analyse géométrique | Repérer les singularités de la modélisation au droit du pic pour en déterminer l’origine géométrique |
| 2 : Analyse des sections d’acier Axi, Axs, Ayi, Ays | Réaliser une première distinction entre les efforts de membrane, de cisaillement et de flexion |
| 3 : Analyse des efforts générant le pic | Détecter la ou les composantes « fautives » et quantifier les efforts |
D.5.2.1 Première analyse : géométrique
L’expérience montre que 90% des pics se situent au niveau de singularités géométriques (poteaux, appuis, intersections voiles/voiles ou voiles/dalles, etc.). Ceci est dû au fait que la modélisation, réalisée à partir des plans moyens ou fibres moyennes ne représente pas les éléments avec leur géométrie volumique réelle (par exemple, une dalle est représentée par un élément plan et les poteaux sur lesquels elle s'appuie, par des élément filaires). De manière imagée, ceci conduit, comme explicité en D.5.1, à prendre en compte des forces appliquées sur des surfaces nulles, donc fatalement à des problèmes numériques. Il est donc indispensable de repérer ces singularités sur le modèle.
a) Exemples de pics liés à la géométrie
Nous partageons ci-après un exemple d’une dalle sur un réseau de poteaux/poutres pour lequel des pics de moments apparaissent au niveau des appuis formés par les poteaux.
Ces pics doivent être interprétés en détail, il est possible de réduire les valeurs des moments dimensionnants en écrêtant au droit des poutres.
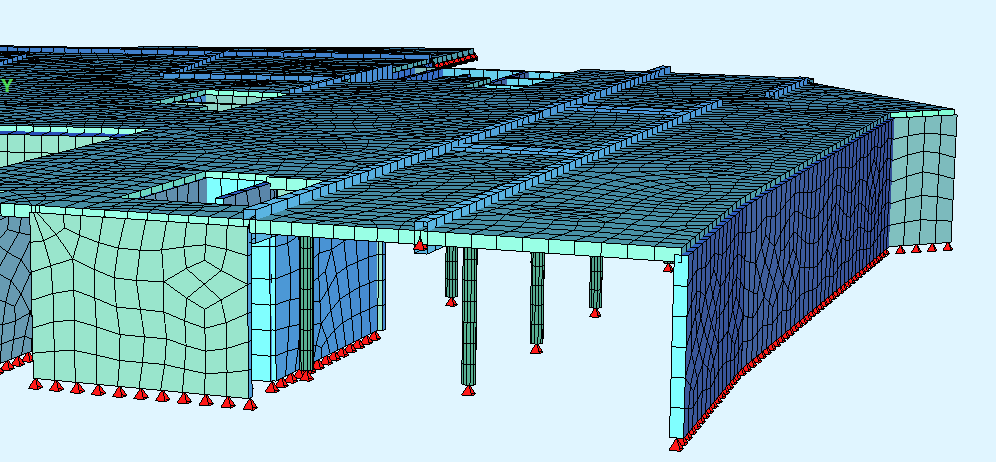
Exemple d’une dalle sur réseau de poteaux et de poutres
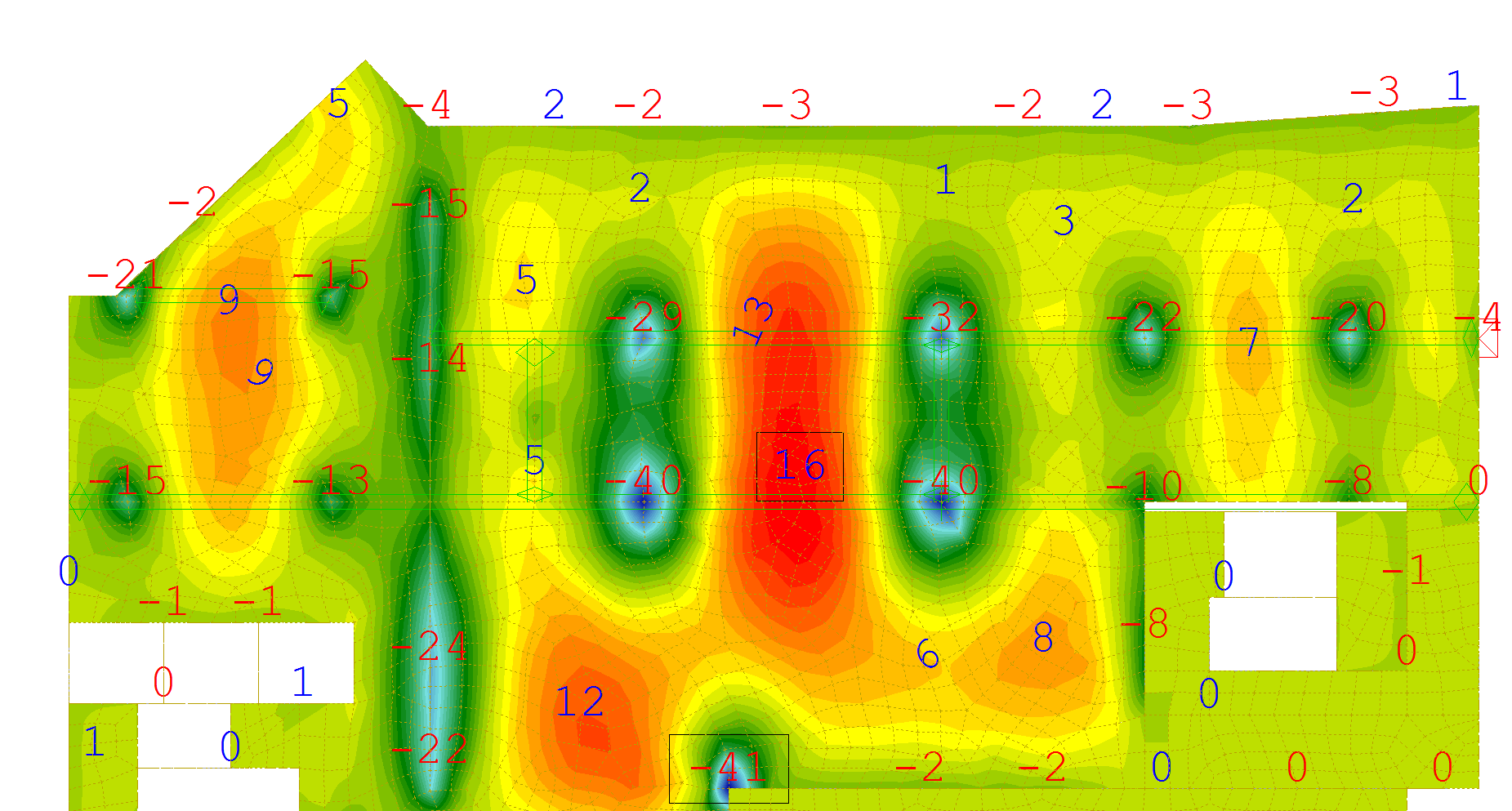
Visualisation des moments fléchissants dans la dalle
Il apparait des pics qu’il est possible d’écrêter au droit des poutres :

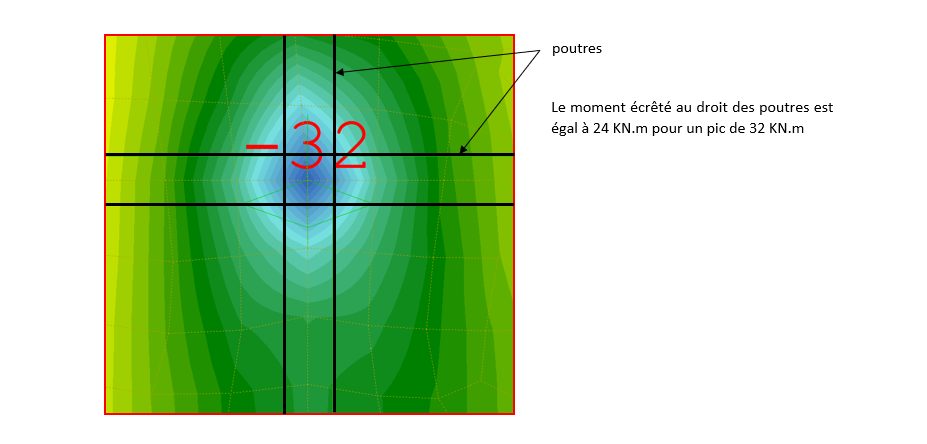
Dans le cas ci-dessus, on écrête conventionnellement au nu des arêtes des poutres ou du poteau en cas de plancher champignon.
Certains logiciels permettent de définir des appuis avec des dimensions en plan pour obtenir directement les efforts aux nus. Exemple d'une dalle de 10×10 m², d'épaisseur 30 cm soumise à son poids propre, appuyé linéairement sur une rive et sur deux appuis ponctuels au droit de deux poteaux à 1 m de chaque coin. L'appui de gauche est un appui ponctuel classique, l'appui de droite est un appui de type poteau, de 50×50 cm².

La représentation des efforts avec et sans réduction des efforts, montre un écart notable sur les valeurs.

Nota: il convient toujours de bien vérifier la méthodologie employée par les logiciels et de s'assurer qu'elle est compatible avec les justifications réglementaires à effectuer.
b) Pics causés par des forces ponctuelles
Le traitement des pics au droit des charges concentrées se rapproche de celui des pics causés par les liaisons ponctuelles. (Une force ou un torseur peut représenter les effets d'un appui ponctuel; il y a une stricte équivalence).
Exemple :
On prend l'exemple trivial d'une charge arrivant via un poteau sur un voile (voile d'épaisseur 30 cm, poteau de 55×30 cm²).

Suivant ce que l'on va chercher à calculer, l'approche ne sera pas la même. Si l'on recherche une descente de charge globale, les approches de gauche, soit via une charge ponctuelle, soit via une barre filaire conviennent parfaitement. Cependant, si l'on s'intéresse aux effets locaux, il faut absolument repasser par une charge répartie pour minimiser le pic de contraintes, ce qui ne facilite pas les calculs automatisés (et ne préjuge pas d'autres calculs manuels à effectuer: diffusion, poinçonnement …).
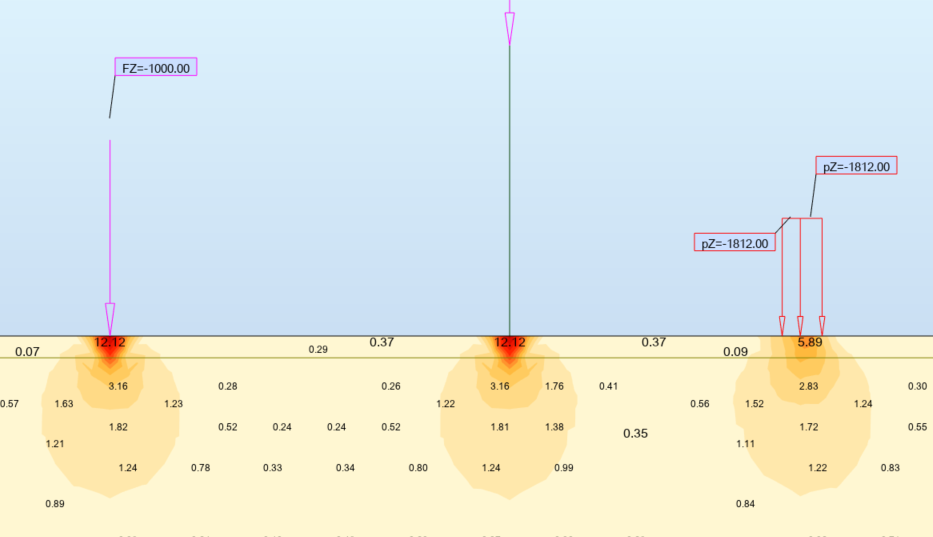
-
Pic lié à la façon de modéliser une charge sur une dalle: cas d'une charge de roue sur un hourdis de pont
Une charge concentrée perpendiculaire à une dalle génère un pic de moment (voir D.5.1). Ce pic est à traiter pour calculer le ferraillage. Il peut être réduit en remplaçant la charge concentrée par un pavé de chargement prenant en compte la diffusion de la charge dans la dalle (diffusion d’une roue sur un hourdis de pont).
Exemple :
On compare le moment longitudinal pour une même charge de 100 kN suivant quatre approches :
-
une force ponctuelle au centre d’une maille ;
-
une force ponctuelle sur un nœud ;
-
une pression correspondant à une force de 100 kN sur une surface de 0.25×0.25 m² (la maille) ;
-
la force de 100 kN/4 = 25 kN répartie aux 4 nœuds encadrant une maille de 0.25×0.25 m².
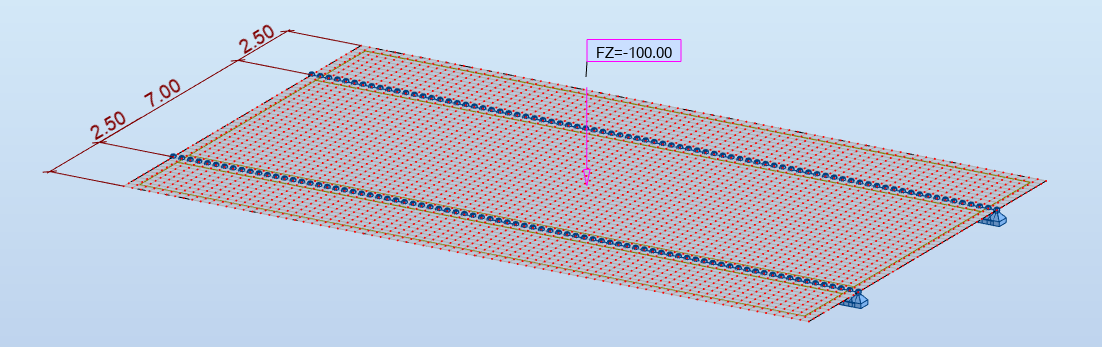
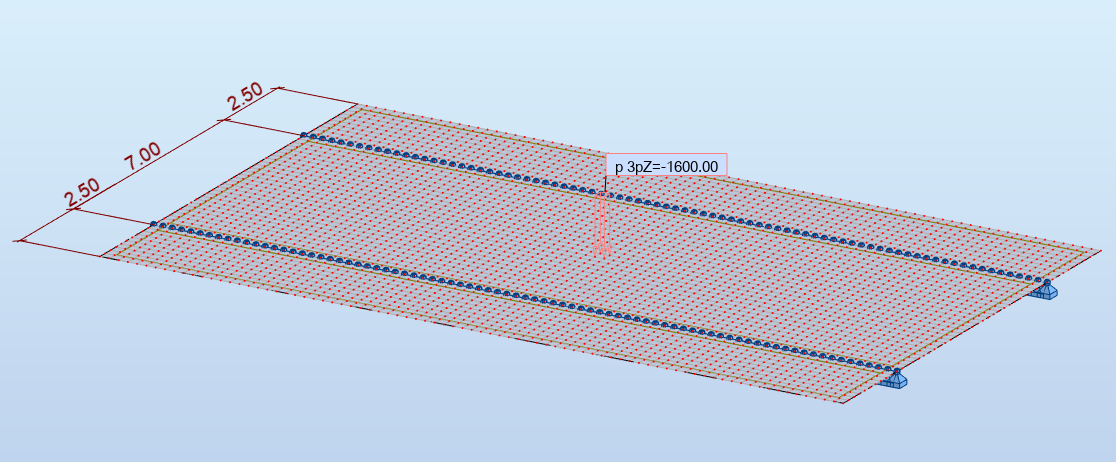
Force de 100 kN au centre d’une maille → Mx=26.62 kN.m/m
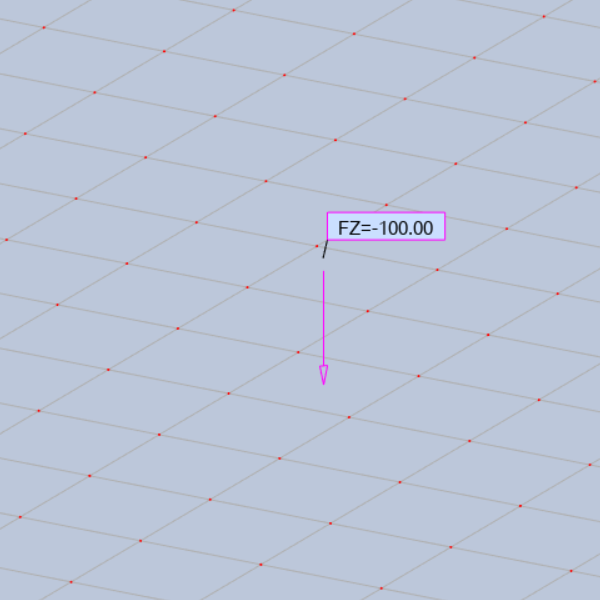
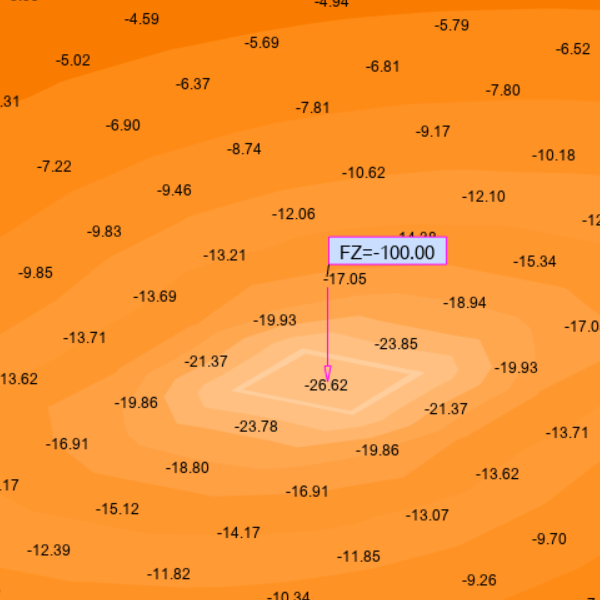
Force de 100 kN sur un nœud → Mx=48.12 kN.m/m
 .
. 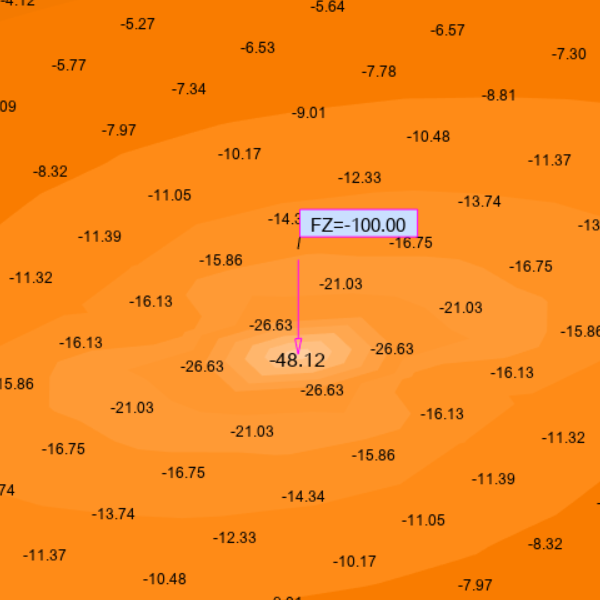
Pression répartie sur une maille → Mx=26.62 kN.m/m
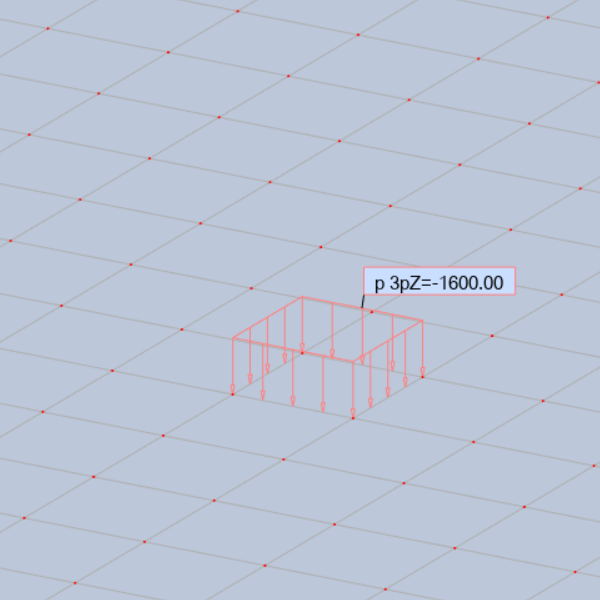 .
. 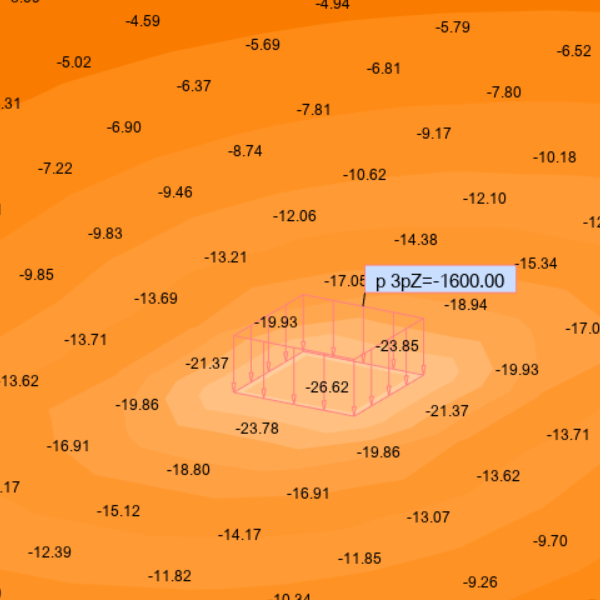
1/4 de force sur 4 nœuds → Mx=26.62 kN.m/m
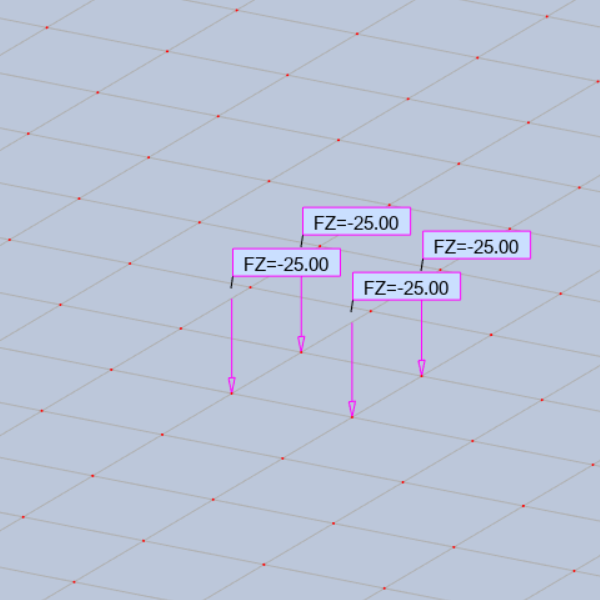 .
. 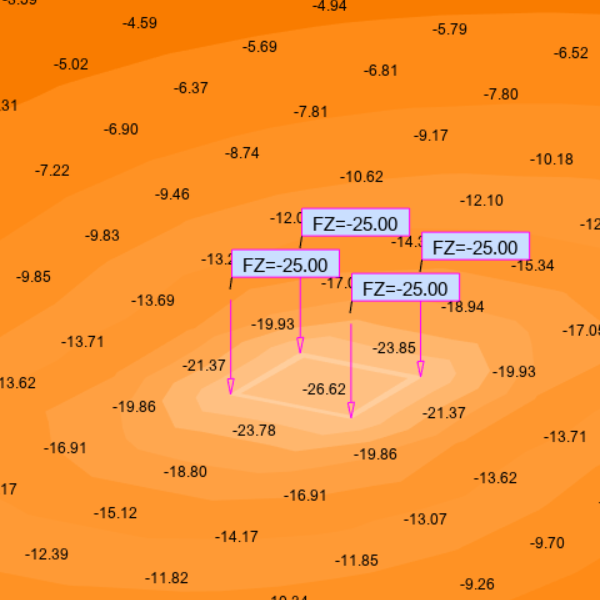
En conclusion, on se rend compte que la modélisation d’une charge répartie par une force ponctuelle peut s’avérer très pénalisante, surtout si cette charge est appliquée sur un nœud du maillage : il vaut mieux passer par des pressions (sachant que le logiciel répartit les charges aux nœuds), ou à défaut scinder la force en plusieurs charges pour éviter le pic d’effort potentiel.
Conseil : éviter la modélisation de forces réparties par une résultante ponctuelle pour le calcul des efforts dans les dalles ou hourdis !
Il convient de s'assurer que la taille des mailles est dans une proportion correcte à la fois avec l'épaisseur de la plaque et la surface d'impact de la charge la plus petite.
En complément, pour illustrer les différents résultats que l'on peut obtenir pour un cas extrêmement simple, le Groupe de Travail a calculé les efforts générés par une roue Br du fascicule 62 titre II, à l'aide de plusieurs logiciels et avec plusieurs approches de lissage. L'étude est disponible dans la partie 3 ou directement ci-après : exemple de modélisation d'une roue Br.
Nota: Dans le cas de structures comportant majoritairement des charges d'exploitation réparties, la taille des mailles aura beaucoup moins d'impact que dans celui d'un hourdis supportant des charges roulantes. Il convient également d'adapter la taille des mailles à la finalité du calcul. Une descente de charges ne nécessite pas le même maillage que le calcul de dimensionnement d'EXE de l'élément de dalle.
Poinçonnement
Il a déjà été évoqué, plusieurs fois, le fait que les éléments finis ne traitaient pas certains sujets comme le décalage des courbes de moments, les écrêtages d'efforts tranchants proches des appuis ou encore les vérifications au poinçonnement.
Sauf cas particuliers, donc, les vérifications liées au poinçonnement restent à faire manuellement. Nous allons l'illustrer sur l'exemple de la charge sur le hourdis de pont montré ci-avant.
Le modélisateur pourrait être tenté de raisonner sur les contraintes de cisaillement moyennées sur la surface poinçonnée issues du calcul EF. Nous nous référons à la formule du BAEL qui a l'avantage de la simplicité. La contrainte de comparaison est simplement la charge divisée par le périmètre de l'impact diffusé au feuillet moyen et par l'épaisseur de la dalle.
Soit τ=100 kN/(4*0.25 m)/0.25 m=400 kPa (la dalle a une épaisseur de 25 cm).
Le calcul EF, lui, aboutit à des contraintes lissées (ici dans la zone la plus défavorable, pas strictement sur le périmètre de diffusion de la charge !) de l'ordre de :
-
τ=5.33 kN (intégrale sur 0.125 m, lue ci-dessous)/0.125 m/0.25 m= 171 KPa ;
-
τ=5.42 kN (intégrale sur 0.125 m, lue ci-dessous)/0.125 m/0.25 m= 173 KPa.
Nous sommes loin des 400 KPa que donne l'approche réglementaire au BAEL - la prise en compte des valeurs EF ne seraient pas sécuritaire. Mais il s'agit de deux approches différentes: les cisaillements dans la dalle servent à calculer les armatures de tranchant et le poinçonnement est un autre type de vérification.

Effort Qxx (KN/m)
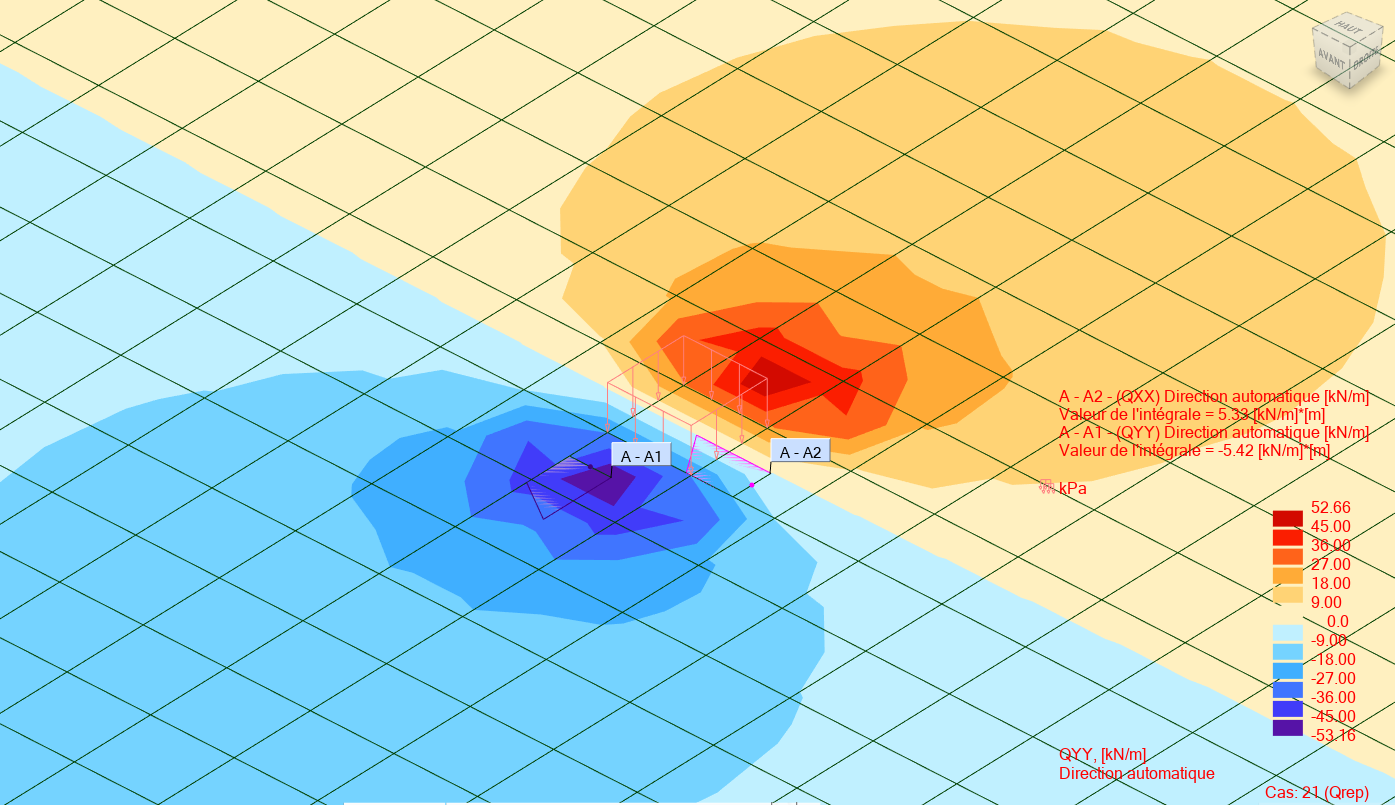
Effort Qyy (KN/m)
Pour le calcul des structures en béton armé, on retiendra que les pics ont pour origine des efforts ou des appuis ponctuels.
c) Pics causés par des problèmes de maillage
Le repérage géométrique du pic permet souvent de détecter les causes.
Exemple d'une incohérence de résultats liée à la modélisation : une construction graphique peut donner l'illusion qu'une arête est commune à deux coques, alors qu'en réalité il y a un décalage extrêmement faible qui conduit à des résultats aberrants. Pour illustrer ce cas, nous prolongeons la dalle d'un exemple ci-avant par un autre élément rectangulaire que nous croyons être strictement dans le même plan que le précédent. Les résultats doivent nous alerter du fait de certains pics qui apparaissent:
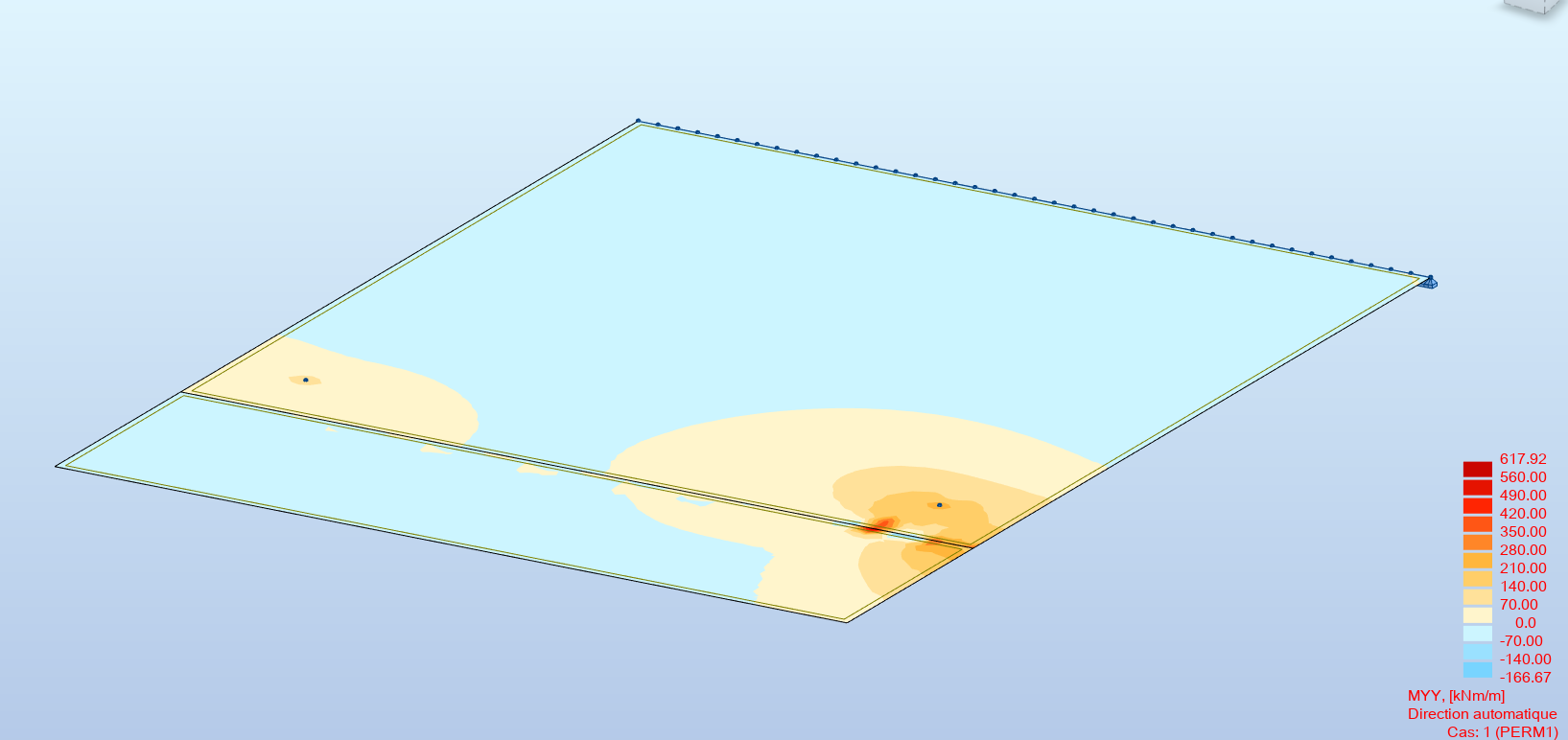
En zoomant, on constate, côté droit, que le raccord ne se fait que sur quelques points (correspondant sans doute à une tolérance géométrique du logiciel) alors que côté gauche on a un décalage, très faible (et provoqué dans le cas présent !) mais qui empêche le raccordement.
On voit sur la figure ci-dessous que les nœuds sur l'arête commune ne sont pas tous raccordés : ceci doit attirer l'attention.
L'observation de la déformée doit également nous alerter :

En cas de difficultés, l’utilisateur pourra préalablement créer lui-même les nœuds de l'arête jointive, le cas échéant avec des éléments de barre qui seront supprimés une fois le maillage fiabilisé et figé. Même si cette approche peut sembler fastidieuse de prime abord, le gain de temps peut largement en valoir la peine.
Il faut rester prudent quant à l’utilisation de corrections automatiques proposées par certains logiciels (en l’occurrence le liaisonnement de nœuds grâce à des liaisons cinématiques) qui peuvent conduire à des pics locaux de contraintes. Dans ce cas, il vaut mieux effacer certaines coques et recommencer proprement certaines parties du modèle. Voir également le § C.3.7.
D.5.2.2 Deuxième analyse : étude des sections d’aciers au droit du pic
Pour nous aider à repérer l’origine du pic, on peut analyser la cartographie des aciers sur chaque face, dans les deux directions de ferraillage. En effet, l’analyse des sections d’aciers Axi, Axs, Ayi et Ays au droit du pic fournit rapidement des informations importantes :
-
des efforts de membranes élevés NXX et NYY se détectent par des sections d’aciers importantes et égales sur les 2 faces. Si de plus les 4 sections d’aciers sont égales alors l’élément travaille en cisaillement dans le plan NXY ;
-
des moments fléchissants élevés MXX et MYY se détectent par des sections d’aciers importantes sur une fibre et très faibles sur l’autre.
Pour illustrer ces propos, le tableau ci-dessous résume les conséquences sur les armatures de chaque composant d’efforts :
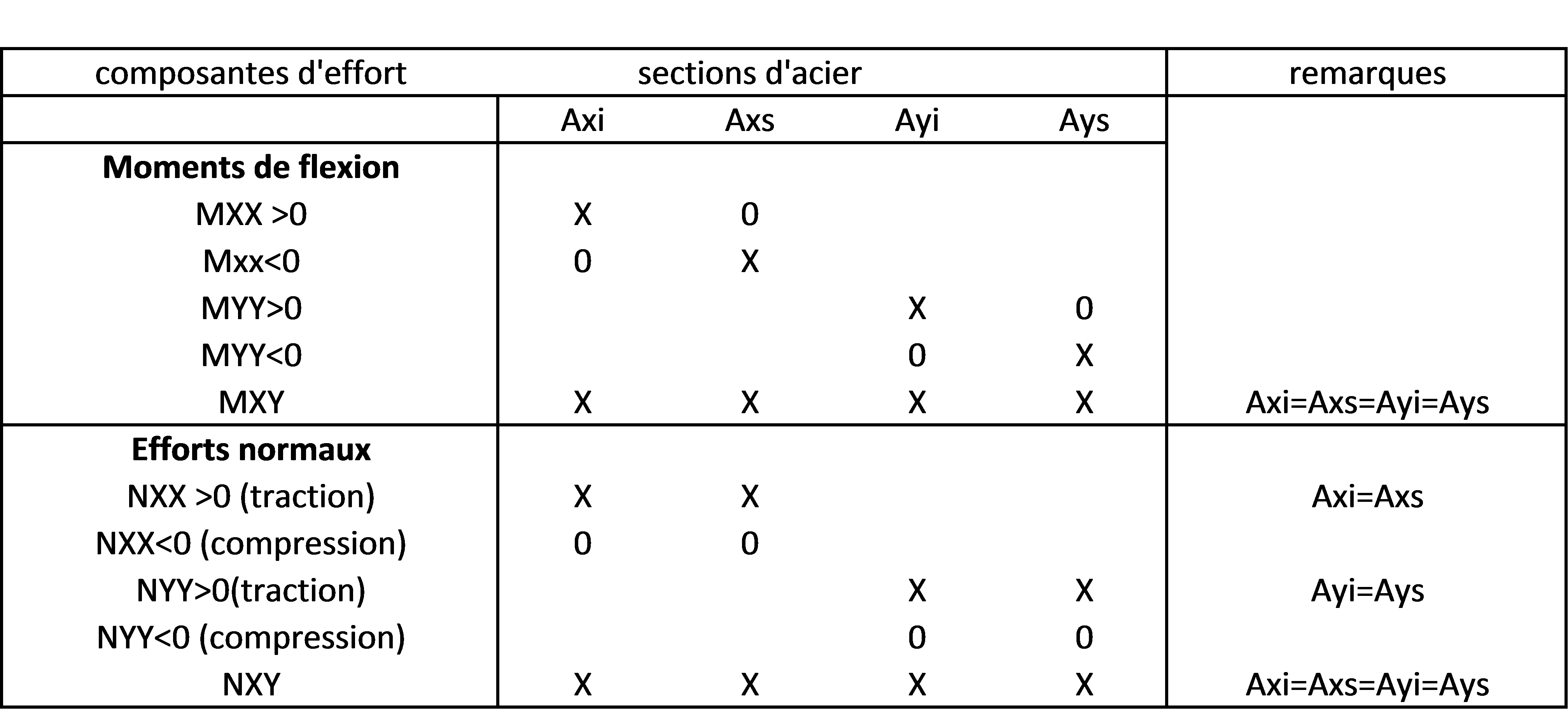
Le code X indique une valeur importante de la section d’acier, le code 0 une valeur faible.
A partir de là on procède à l’analyse décrite ci-après.
D.5.2.3 Troisième analyse : étude des efforts au droit du pic
Si les deux analyses précédentes ne sont pas suffisantes pour expliquer le pic, il est nécessaire alors d’étudier en détail les composantes des efforts pour en déterminer leurs intensités et repérer les cas de charges dimensionnants.
Cette analyse qui est souvent longue et délicate dans le cas d’une modélisation complexe, peut être grandement simplifiée pour les modélisations simples en procédant à des cartographies d’efforts ou des coupures locales.
D.5.3 Résolution du pic : détermination du ferraillage final
Après avoir compris le fonctionnement de la structure et maîtrisé les cheminements des efforts, l’ingénieur a tous les éléments pour solutionner le pic et en déduire le ferraillage strictement nécessaire.
D.5.3.1 Cas où les écrêtages ou lissages ne sont pas possibles
Dans certains cas, l'étude du cheminement des efforts montre que les pics sont réels et ne peuvent être écrêtés, c'est le cas des linteaux qui font apparaître des pics très importants à leurs extrémités, ce qui est logique car ce sont des poutres bi-encastrés qui doivent être calculées selon les règles de la RDM et du béton armé (poutre bi- encastrée soumise à un cisaillement constant).
D.5.3.2 Ecrêtage des moments sur appuis
L’article 9.5.3.2.2 de l’EC2-1 permet d’écrêter les moments au nu des appuis (voiles)
a) Poutre appuyée sur un poteau - exemple 1
Considérons l’exemple d’une dalle comportant 2 travées de 6 m et chargées uniformément par 25 kN/m².
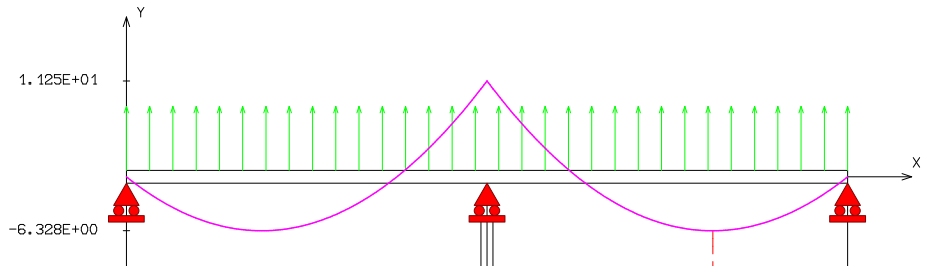
Les moments théoriques sont de -11.2 kN.m sur appuis et de 6.3 kN.m en travée
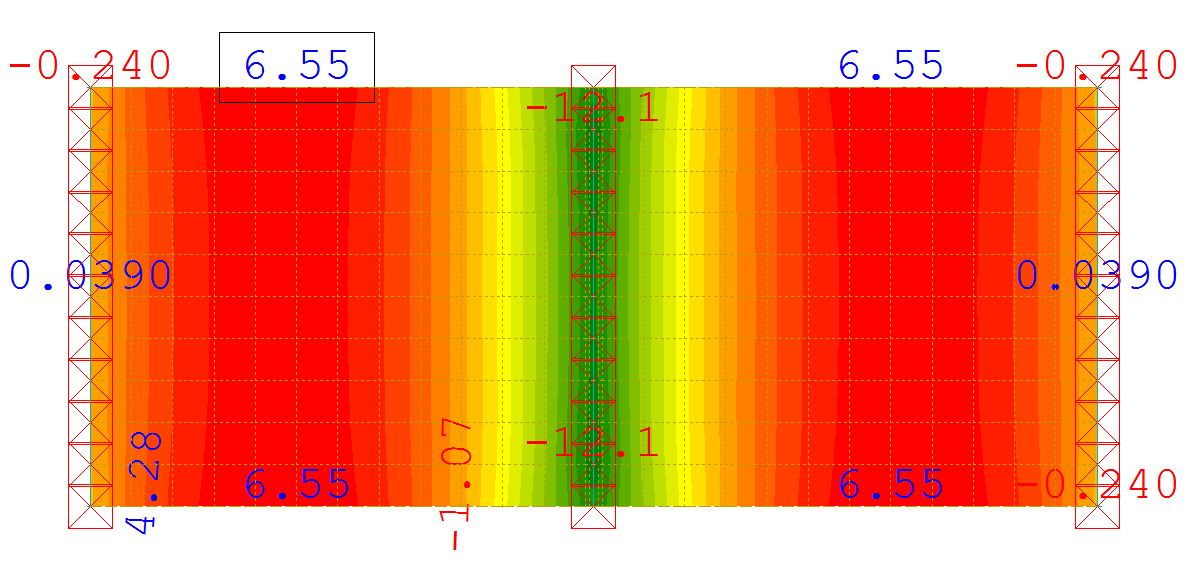
Le logiciel EF fait apparaitre un pic de -12.1 kN.m sur appui qui est réel.
Ecrêtage au nu du voile :
Pour obtenir le moment au nu du voile (ép. = 20 cm), l’utilisateur a plusieurs solutions :
-
soit réaliser des coupures au niveau de l’appui ;
-
soit ne pas visualiser la zone d’appui (mais cela nécessite une adaptation du maillage) ;
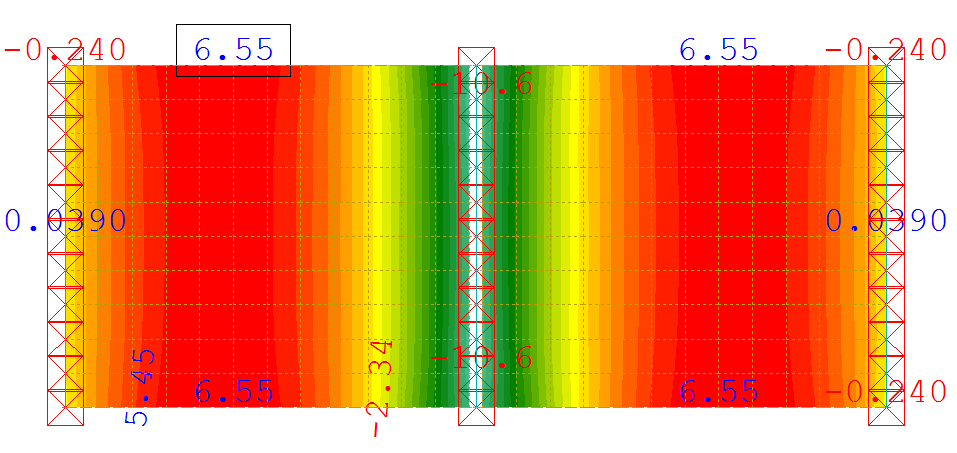
Moment au nu des appuis = -10.6 kN.m
-
soit adapter le maillage afin que la largeur de la maille sur appuis soit égale à l’épaisseur du voile, comme représenté ci-dessous.
Le moment au centre de la maille représentera alors le moment au nu de l’appui.
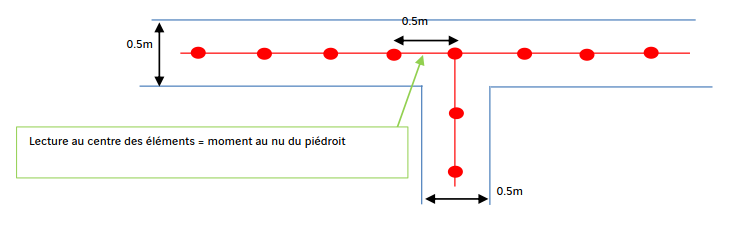
Le même type de réflexion et d'approche est à mener pour écrêter l' effort tranchant, le cas échéant.
b) Poutre appuyée sur un poteau - exemple 2
L’exemple ci-dessous montre deux manières de modéliser une structure poteau-poutre simple pour mettre en évidence les effets des dimensions réelles des structures.
Le principe est le suivant, pour une largeur hors plan de 1 m :
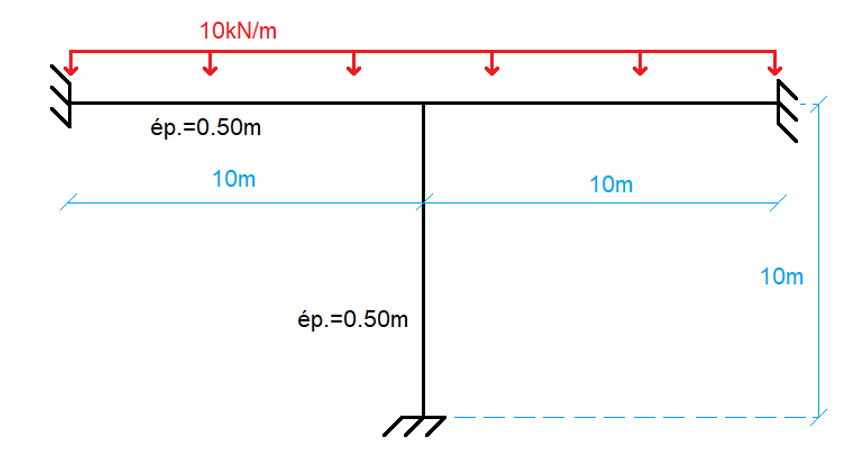
Dans un premier temps, un modèle filaire permet de calculer les moments, au niveau de l’appui central (vue tronquée) :
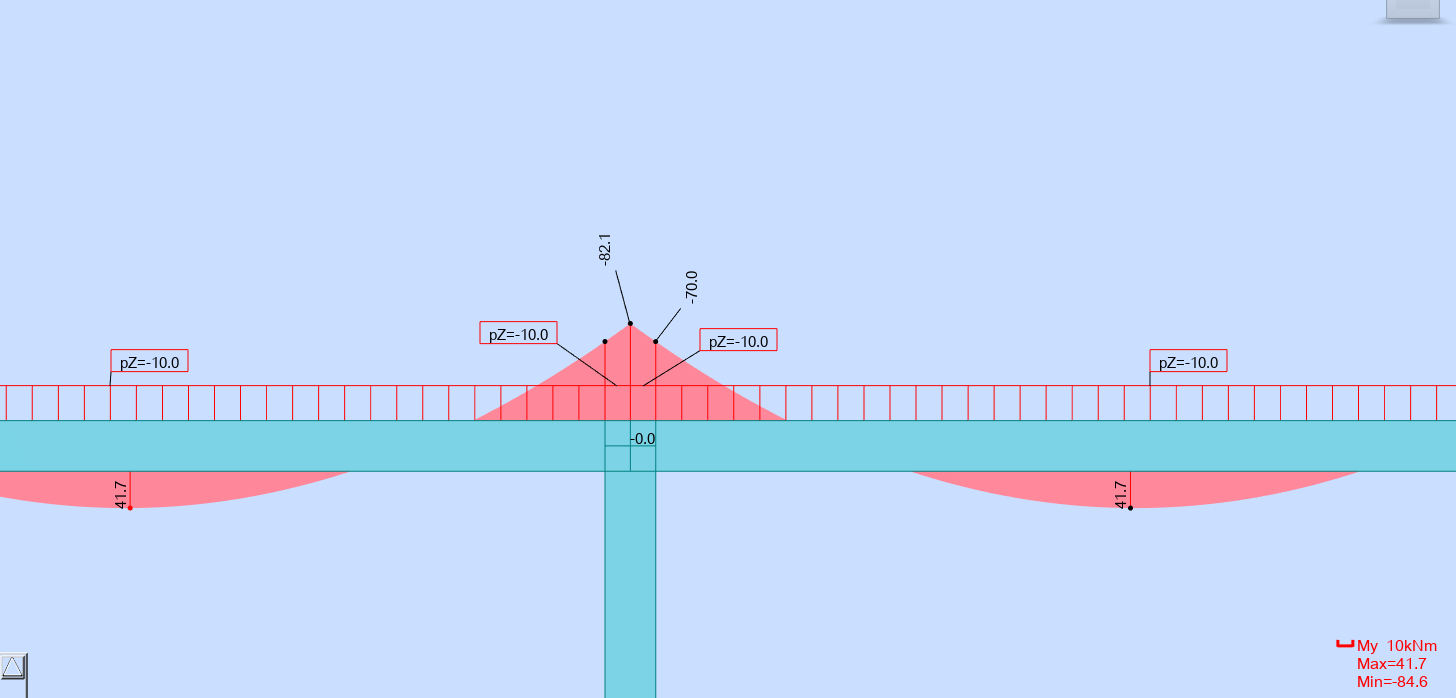
Le moment sur l’appui central vaut 82.09 kN.m, ce qui donne une contrainte extrême en fibre supérieure et en fibre inférieure de 6M/(bh²)=(6*82.09)/(1.0*0.5²) = 1970 kPa = 1.97 MPa. La contrainte au nu vaut, quant à elle (6*70.00)/(1.0*0.5²) = 1680 kPa = 1.68 MPa.
Ci-dessous le résultat (en contraintes) du même calcul effectué sur un modèle avec des plaques, bloquées en déplacement hors plan. Ce modèle permet de représenter le comportement en coupe, avec les épaisseurs réelles des éléments. (vue tronquée)

La contrainte obtenue en fibre supérieure est de 1.58 MPa. (Celle en fibre inférieure n'est pas représentative du fait qu'elle est calculée dans une zone singulière que constitue l'angle droit).
Ce modèle met en évidence la légitimité des écrêtages effectués dans la pratique.
D.5.4 Lissage des ferraillages
La méthode ci-après issue d’une pratique courante dans le domaine du Génie Civil Nucléaire permet de donner des règles simples pour lisser les ferraillages.
Son application reste néanmoins soumise au jugement de l’ingénieur. En particulier, dans le cas de planchers de bâtiments courants ou de hourdis de ponts, ces valeurs sont sans doute trop favorables et il semble loisible de réduire la taille du lissage à la moitié des valeurs ci-dessous, par conséquent plafonner cette taille à 2h (h étant l'épaisseur de la dalle).
Dans ce cadre, le lissage des sections d’armatures longitudinales et des armatures d’effort tranchant doit se faire :
-
entre éléments adjacents (et non successifs par rapport à la direction du ferraillage) ; le lissage se fait perpendiculairement à la direction du ferraillage ;
-
sur une distance raisonnable (jugement de l’ingénieur) et inférieure à une valeur fonction de l’épaisseur de la plaque et de la portée de la plaque.
La pratique courante actuelle est de faire la moyenne sur les résultats de trois éléments : l’élément pour lequel le maximum est observé et les deux éléments adjacents, en limitant la largeur sur laquelle s’effectue la redistribution à 4 fois l’épaisseur de la dalle (voir le tableau ci-après).
Ex : si la taille des éléments est de 1 m, faire la moyenne sur trois éléments revient à faire la moyenne sur une largeur de 3 m. Pour une dalle de 0.5 m, cette largeur est limitée à 4 fois l’épaisseur de la dalle, soit 2 m, ce qui conduit à faire la moyenne sur seulement deux éléments.
Il faudrait aussi limiter la largeur de répartition en fonction de la portée de la dalle ou de la hauteur du voile, en effet plus la portée (ou la hauteur) est faible, plus la largeur de répartition doit être réduite.
Règles proposées pour le lissage des pics de ferraillage longitudinal des dalles (issus des efforts N, M)
Elles sont présentées dans le tableau qui suit. Elles sont valables pour une dalle soumise essentiellement à des efforts de membrane et à des moments de flexion dus à des charges réparties hors du plan, et avec un maillage suffisamment fin qui présente :
-
un nombre impair d’éléments selon les deux directions de portée ;
-
au minimum de 5 éléments selon la petite portée (7 éléments si possible) ;
-
une taille de maillage égale à l’épaisseur des éléments porteurs.
| Largeur sur laquelle il est possible de lisser les sections d’armatures longitudinales et transversales | Limitation de la largeur de distribution en fonction de l’épaisseur h de la plaque | Limitation de la largeur de distribution en fonction de la portée L de la plaque |
| Zone où la redistribution des efforts peut se faire dans les deux directions | 4h | 0.5 L |
| Zone où la redistribution des efforts ne peut se faire que dans une seule direction (en bordure de trémie) | 2h | 0.25 L |
Pour des charges concentrées hors plan, il faut aussi tenir compte de la distance de la charge à l’appui et de sa diffusion.
Les pics de ferraillage se trouvent fréquemment en bordure de trémie, dans ce cas, la redistribution des efforts ne peut se faire que dans une direction et donc sur des largeurs limitées :
-
si un ferraillage complémentaire au ferraillage courant est nécessaire, on a toujours intérêt à le placer au plus près des bords de la trémie.
-
si après lissage du ferraillage comme spécifié ci-dessus, le ferraillage courant suffit, il est cependant recommandé de placer un ferraillage complémentaire en bordure de la trémie si plus d’une armature courante est coupée par la trémie dans une des deux directions.
Pour les petites ouvertures (en particulier les fourreaux) s’insérant dans la maille du ferraillage ou provoquant l’interruption d’une seule armature, il est possible de ne pas ajouter un ferraillage complémentaire.
Règle proposée pour le lissage des pics de ferraillage longitudinal dans les éléments membranaires (voiles)
Pour des éléments soumis à des efforts membranaires de traction, la redistribution ne peut s’effectuer que dans une direction.
| Largeur sur laquelle il est possible de lisser les sections d’armatures longitudinales et transversales | Limitation de la largeur de distribution en fonction de l’épaisseur h de la plaque | Limitation de la largeur de distribution en fonction de la portée L de la plaque |
| La redistribution des efforts ne peut se faire que dans une seule direction (en bordure de trémie) | 2h | 0.25 L |
Dans les voiles de contreventement soumis à un moment de flexion d'axe perpendiculaire au plan du voile, la contrainte membranaire de traction varie linéairement.
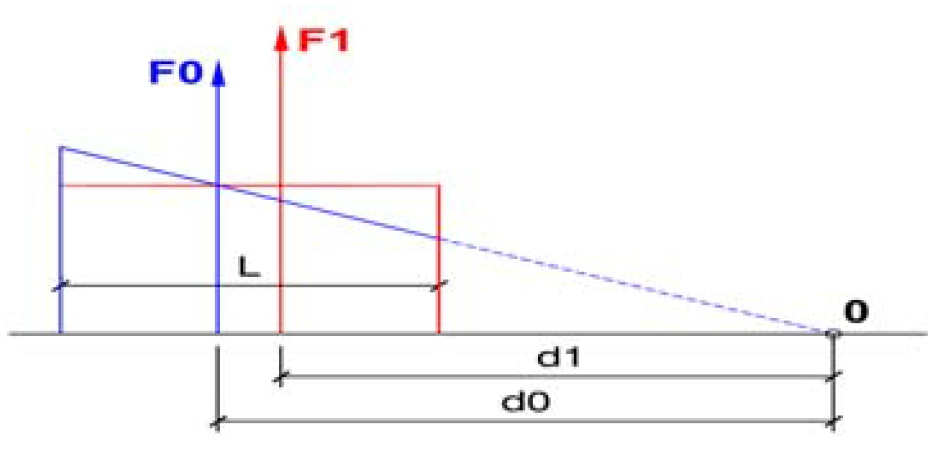
Lorsque l’on lisse les pics d’armatures, il faut étendre le ferraillage lissé sur une longueur suffisamment grande pour conserver la capacité de flexion : F1 x d1 > F0 x d0, où :
-
F1 = effort résultant repris par les armatures après lissage sur la longueur L ;
-
d1 = distance entre la résultante F1 et le point de moment nul ;
-
paramètres ci-dessus avec indice 0 = avant lissage.
Pour des éléments soumis à un cisaillement de membrane, il est possible de reporter une partie de la section requise AX vers la section AY, si cette dernière est surabondante et réciproquement. En effet les logiciels courants utilisent la méthode de Capra Maury qui optimise la somme des sections d’armatures AX + AY.
La section AY peut être parfois déterminée par la condition de ferraillage minimale et la section AY prévue est alors supérieure à la section AY requise à partir du calcul de résistance, permettant ainsi une redistribution des sections d’armatures. Il faut ensuite vérifier la résistance de la section avec les nouvelles sections d’armatures.
Conclusion concernant le lissage des pics de ferraillage longitudinal
Dans tous les cas, il faut tenir compte de l’origine des besoins d’acier en analysant les efforts (Nxx, Nyy, Nxy, Mxx, Myy, Mxy) et interpréter les résultats, au cas par cas, avec une approche «béton armé».
En général, le ferraillage des voiles provient majoritairement des efforts de membranes (Nxx,Nyy,Nxy), les efforts de flexion (Mxx,Myy,Mxy) étant alors négligeables. Par contre le ferraillage des planchers est dû principalement aux efforts de flexion (Mxx,Myy,Mxy), et dans certains cas par des efforts de membrane (Nxx,Nyy,Nxy) lorsque le bâtiment est soumis à des efforts horizontaux (vent, séisme) ou à des irrégularités (poutres voiles).
Une poutre voile est un bon exemple d'irrégularité produisant des efforts horizontaux dans les planchers: l'exemple ci-après reprend la poutre voile reposant sur 2 poteaux étudiée au chapitre D.4.5, mais en modélisant un plancher inférieur; les contraintes de traction visualisées en rouge montrent que le tirant inférieur se forme non seulement à la base du voile mais aussi dans le plancher inférieur :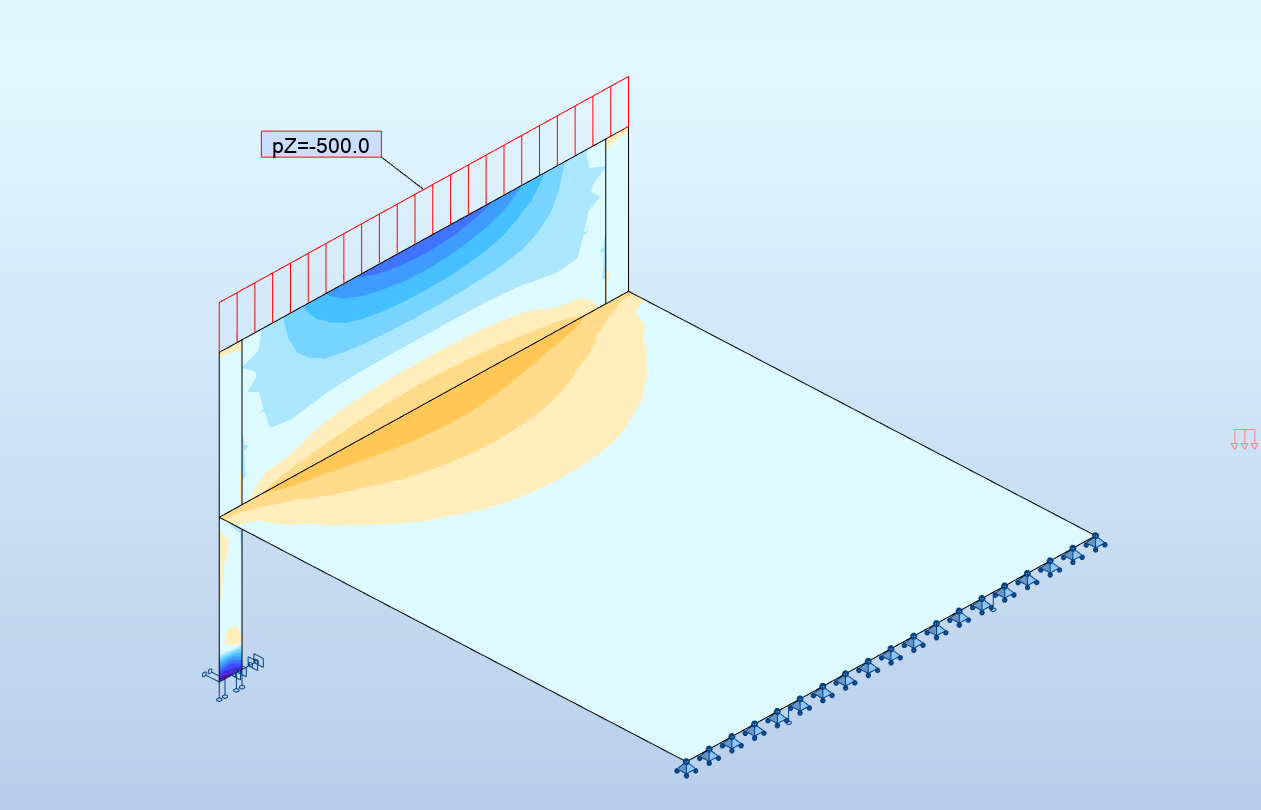
Les tractions sont encore plus importantes (ici +50%) dans le cas d'ouvertures à la base du voile :
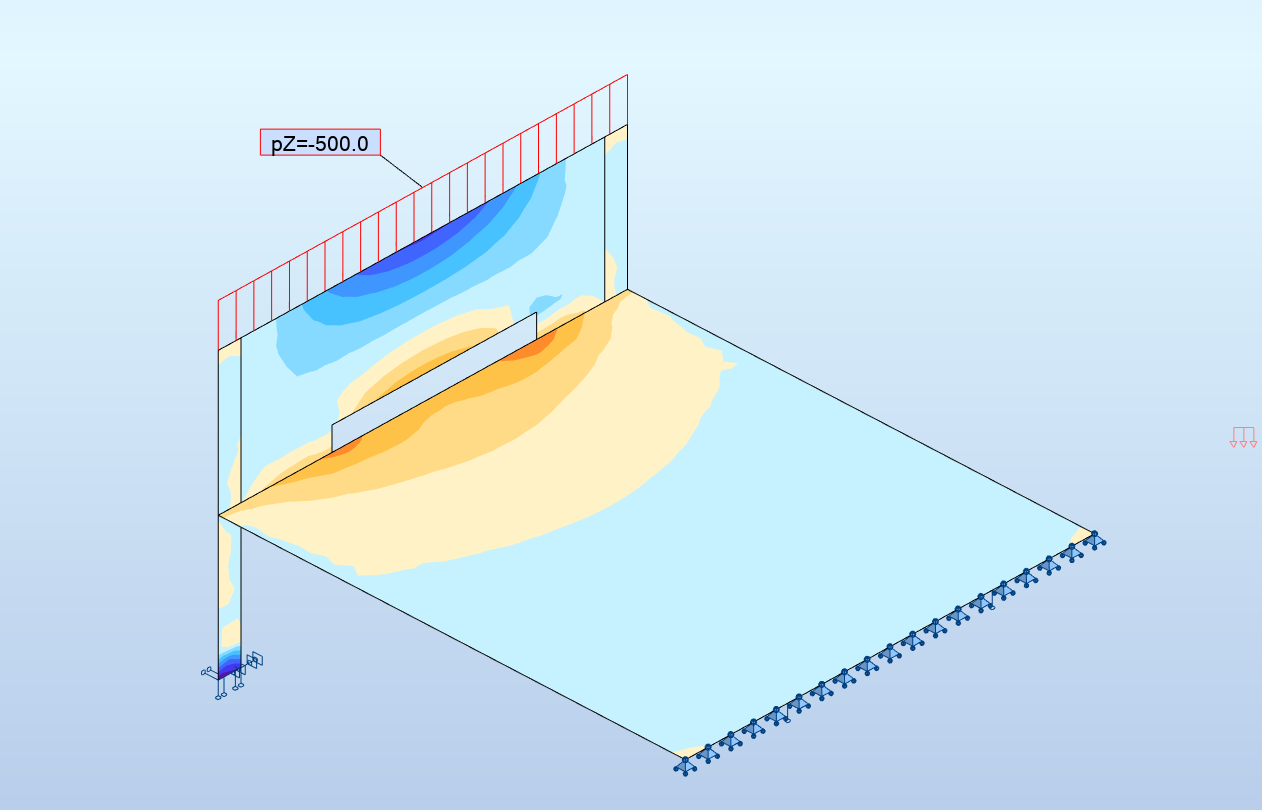
Règle proposée pour le lissage des pics d'armatures d’effort tranchant (perpendiculaire aux éléments)
Généralement, les pics d’effort tranchant perpendiculaire aux éléments se produisent à l’intersection de plusieurs plaques
Les pics d’armatures d’effort tranchant apparaissent souvent lorsque l’effort tranchant est concomitant avec une traction importante.
Pour rappel, pour la justification du béton armé, la concomitance d’un effort tranchant avec une traction nécessite une attention particulière car cela signifie qu’il n’y a pas formation de bielle de compression dans le béton et donc un risque de rupture.
La résolution de ce type de pic nécessite de revenir aux efforts, de moyenner les efforts tranchants et les efforts normaux et de recalculer les armatures.
Illustration des approches:
Exemple 1 :
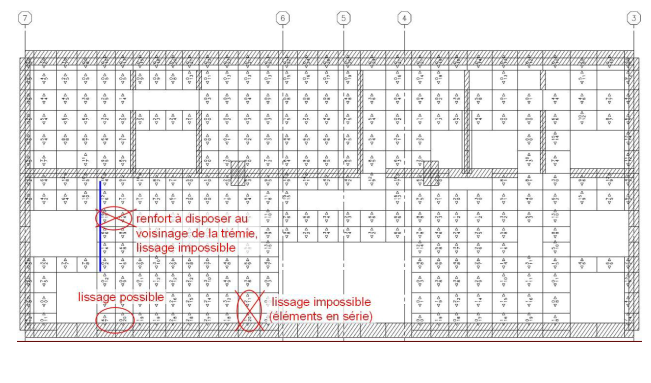
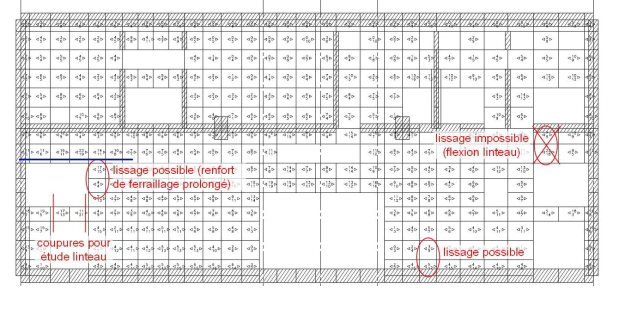
Exemple 2 :
Les pics de ferraillage lus sur les cartes sont lissés selon le principe suivant :
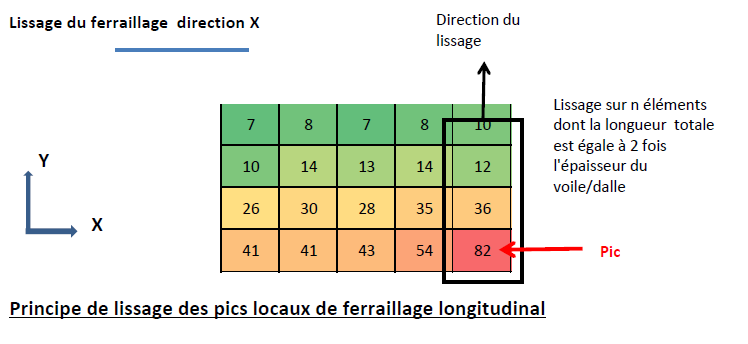
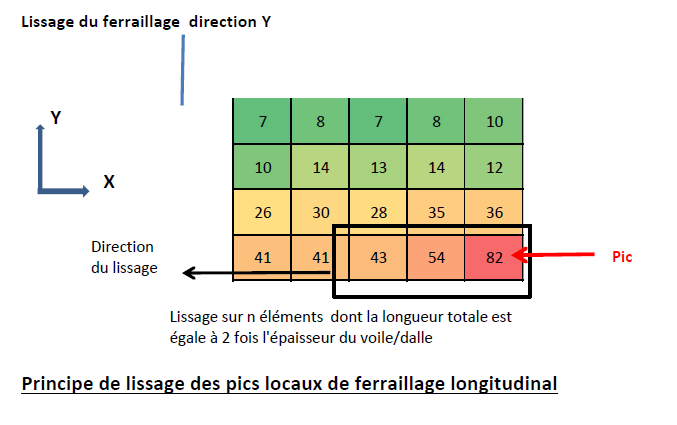
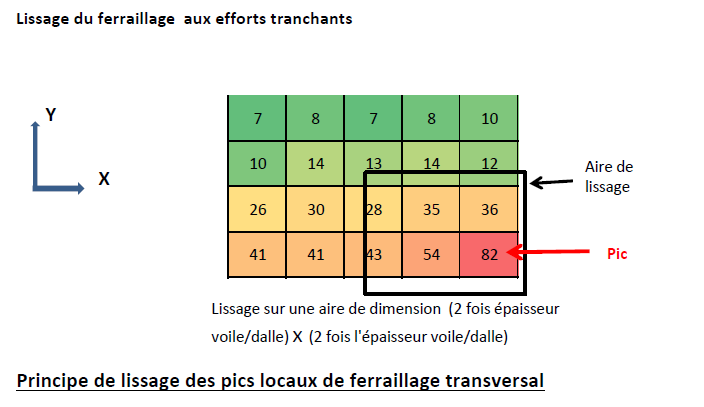
D.5.5 Répartition des efforts dans les poutres et les dalles
Il est important de rappeler que, sauf exception, le calcul des efforts internes dans les éléments est un calcul élastique linéaire avec un module de béton constant.
Les pics d’efforts déterminent souvent une fissuration de la section de béton armé et donc une réduction locale des efforts au pic et une redistribution des efforts.
Il est parfois utile - et c’est admis - de faire une redistribution des moments de flexion. Il faut faire la distinction entre :
-
l’Etat Limite de Service (possibilité de redistribution limitée, prenant en compte l’affaiblissement de la rigidité de la section à cause de la fissuration du béton dans la zone fortement sollicitée du pic) ;
-
l’Etat Limite Ultime (possibilité de redistribution plus large : même phénomène que celui pris en compte pour l’ELS avec en plus les possibilités de redistribution plus larges indiquées dans l’Eurocode 2 aux paragraphes 5.5 « Analyse élastique-linéaire avec redistribution limitée des moments » et 5.6 « Analyse plastique ».
Il faut cependant signaler que les recommandations professionnelles pour l’application de la norme NF EN 1992-1-1 (NF P 18-711-1) autorisent, pour les bâtiments, à utiliser à l’ELS, une redistribution des moments avec les mêmes coefficients de redistribution qu’à l’ELU.
Dans le cadre des Eurocodes, le rapport δ du moment après redistribution au moment élastique de flexion, doit être supérieur ou égal à 0,7 pour des armatures longitudinales de classe A et à 0,8 pour des armatures longitudinales de classe B ou C.
Cette redistribution des moments dans une poutre continue est possible si la poutre ne participe pas au contreventement. Elle est plus délicate si la poutre appartient à une ossature en portique (attention aux moments élastiques provenant de l’effet portique).
Il ne faut pas oublier de prendre en compte l’incidence de la redistribution des moments fléchissant sur les efforts tranchants.
$translationBooksD.6 Comprendre et analyser les pics (cas d’un assemblage métallique)
D.6 Comprendre et analyser les pics (cas d’un assemblage métallique)
Les résultats d’un calcul réalisé sur un modèle éléments finis surfaciques (éléments de type plaques ou coques) peuvent présenter des pics de contraintes (ou singularités). La présence de pics de contraintes n’est pas contrariante s’ils sont localisés dans des zones hors d’intérêt vis-à-vis des objectifs de l’étude et si leur présence est justifiée.
Il faut garder à l'esprit qu'un pic de contraintes, c'est à dire une contrainte très élevée, doit concerner deux ou trois nœuds, voire un seul nœud au maximum (mais la structure peut cependant présenter plusieurs pics de contraintes).
Lors du dimensionnement d’un assemblage de tôles soudées entre elles (caisson de pont métallique au droit d’un appui par exemple), la réalisation d’un modèle aux éléments finis surfaciques s’avère nécessaire pour une prise en compte correcte de la diffusion des efforts. Et bien sûr, à partir du même modèle, les contraintes dans les tôles pourront être extraites pour procéder au dimensionnement de l’assemblage de ces tôles.
Néanmoins, l’idée générale restera de toujours conserver un regard critique sur les résultats obtenus. Ceux-ci devront être analysés convenablement avant de pouvoir les considérer fiables vis-à-vis des objectifs de l’étude menée.
Cette analyse sur la fiabilité des résultats bute souvent sur l’interprétation de la présence éventuelle de pics de contraintes.
L’objet de ce paragraphe est de donner des pistes pour aider le modélisateur à qui il appartient d’évaluer le caractère gênant ou non d’un pic de contrainte.
Les apparitions de pics de contraintes peuvent avoir différentes origines dont les principales sont :
-
la présence ou l’omission de détails tels que des congés de raccordement ;
-
des incohérences de maillage ;
-
la mise en place des chargements et des conditions aux limites.
D.6.1 Modélisation – Détails
Avant de se lancer dans la modélisation surfacique d’un assemblage de tôles, il est indispensable de connaître et de maitriser les outils CAO du logiciel et ses capacités de maillage.
Il est d’usage lors de la création de la géométrie de négliger certains détails. Deux cas parmi d’autres :
-
les congés de raccordement – si les congés de raccordement d’une ouverture dans l’âme d’une poutre ne sont pas représentés, on obtiendra inévitablement des concentrations de contraintes d’autant plus élevées que les sollicitations de l’âme sont importantes et que l’angle est aigu (cas des arêtes d'ouverture non perpendiculaires) ;
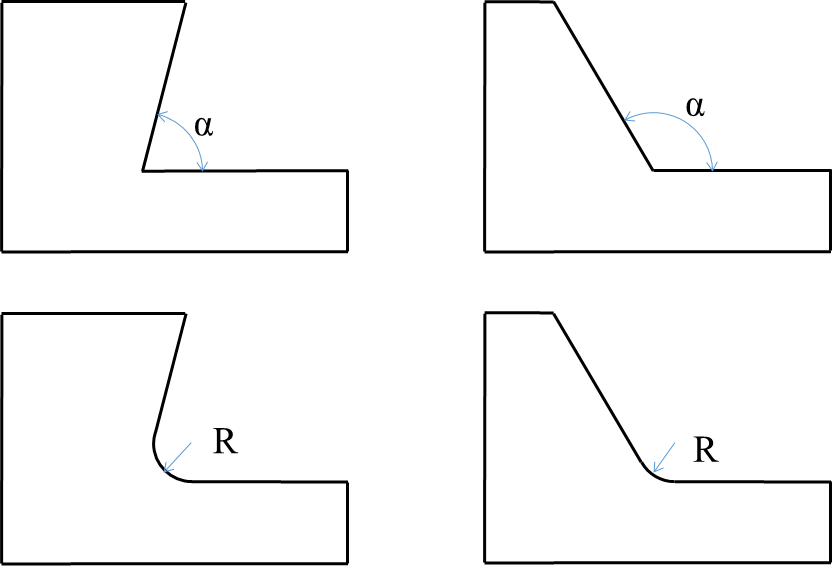
Note 1 : La modélisation d’un congé de raccordement ne créera plus un pic de contrainte, mais une simple concentration de contraintes. Les abaques de concentrations de contraintes sont basés sur ce type de modélisation.
Note 2 : En mécanique de la rupture, le modèle de fissure caractérisé par un angle nul est un cas particulier utilisé pour modéliser la propagation des fissures qui est basée sur la notion de facteur d’intensité des contraintes.
-
les raidisseurs transversaux – les poutres principales d’un ouvrage d’art nécessitent, au droit des zones d’appuis, des raidisseurs transversaux. La modélisation de ces raidisseurs est souvent nécessaire au vu des efforts pouvant transiter dans cette zone et venant solliciter localement l’âme. De par les règles de l’art, ces raidisseurs ont une géométrie particulière et trop souvent cette géométrie est simplifiée à l’extrême au cours de la modélisation ;
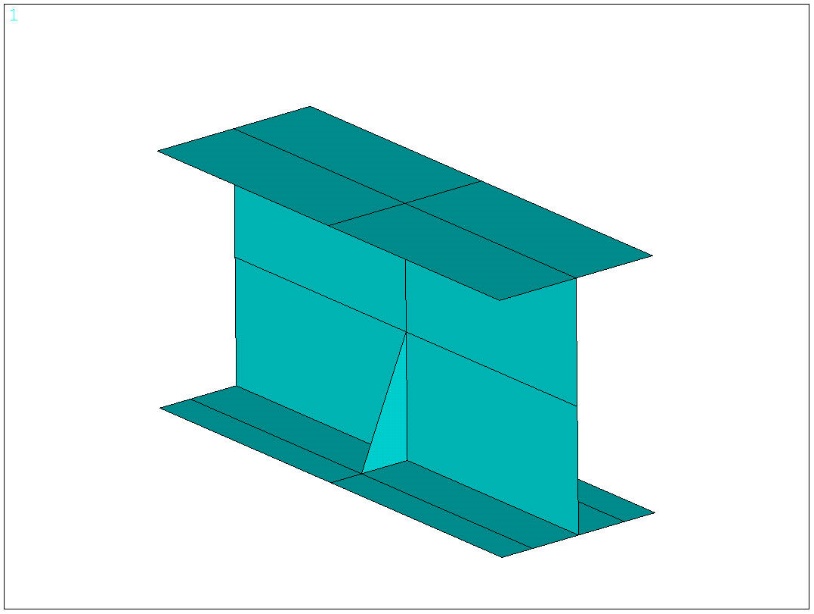
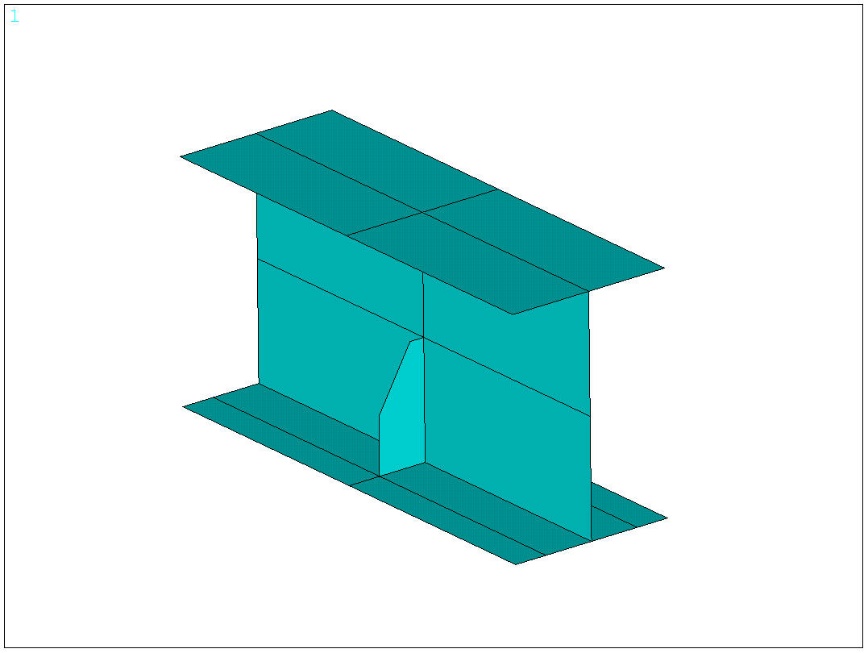
Géométrie réelle / Géométrie simplifiée
La transition des efforts peut ne pas être affectée mais le maillage du raidisseur sera à piloter de manière à ne pas se retrouver avec des éléments dégénérés pouvant créer des singularités. Et à la pointe du raidisseur, un pic de contraintes peut apparaître lequel en cas de mauvaise interprétation peut amener à de fausses conclusions. Voir également le § C.3;
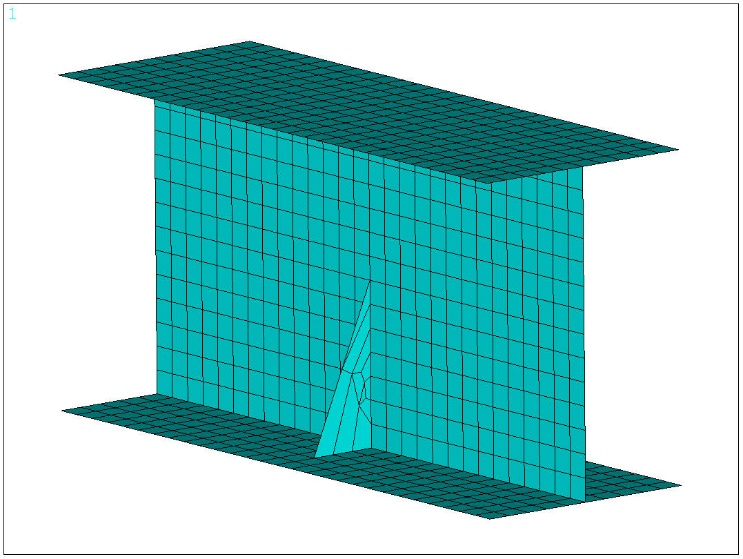
-
les détails tels que congés de raccordement, trous de souris, chanfreins, etc. peuvent donc ne pas être modélisés si leur localisation est hors d'une zone d’intérêt. Le temps passé à la modélisation de détails peut ne pas être négligeable, mais si l’objectif de la simulation est de calculer une contrainte ou une déformation dans une zone présentant de tels détails, il est indispensable de les modéliser et, de plus, d’y associer un maillage représentatif.
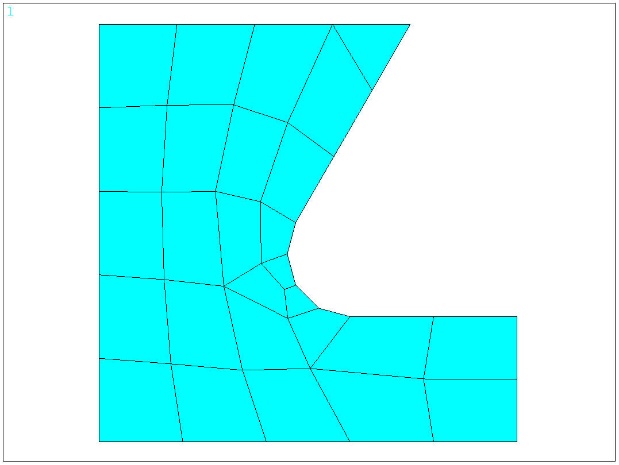 .
. 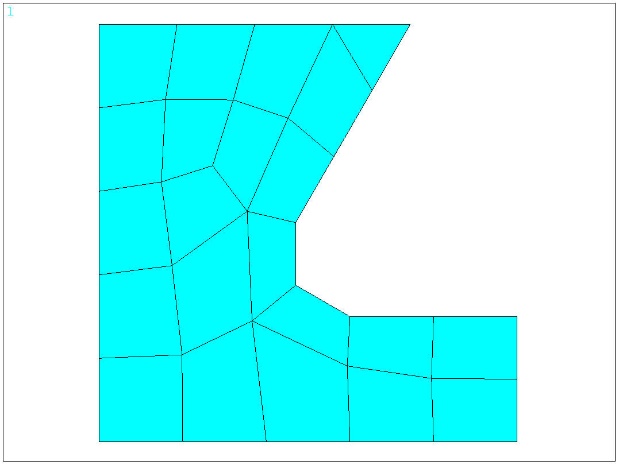
Maillage non représentatif / Maillage représentatif
En l’absence de plans détaillés des détails constructifs à modéliser, on s’appuiera sur les dispositions constructives et règles de l’art, lesquelles, en matière d’assemblages métalliques (congés de raccordement, plats locaux, raidisseurs, etc.), donnent des bases conduisant en général à une diffusion satisfaisante des efforts. Par exemple, les recommandations de la CNC2M pour le dimensionnement des poutres en acier avec ouvertures dans l’âme selon la NF EN 1993 précisent que, pour une ouverture rectangulaire, le rayon des congés de raccordement doit être supérieur ou égal à deux fois l’épaisseur de l’âme sans être inférieur à 15 mm, ou encore qu'une ouverture isolée présentant une dimension maximale inférieure à 10% de la hauteur de l'âme de la poutre n'est pas considérée comme significative (cette ouverture doit néanmoins être prise en compte lors de la vérification de la section).
Dans certains cas, on ne peut pas négliger la prise en compte des détails (voir également le § C.2.2). Par exemple, lors d’une vérification à la fatigue des assemblages d’une dalle orthotrope, on peut utiliser des modèles simplifiés de calcul décrits dans les règlements de calcul. Mais ces modèles sont sécuritaires et, si la résistance à la fatigue n’est pas justifiée avec ces approches simplifiées, deux possibilités s'offrent au projeteur :
-
soit modifier la géométrie des pièces assemblées, ce qui est souvent difficile en phase d’exécution ;
-
soit procéder à un calcul plus raffiné sur un modèle éléments finis en plaques.
Pour tenir compte des effets du passage d’un véhicule (effets longitudinaux et transversaux, lignes d’influence), il peut être nécessaire de modéliser une longueur assez conséquente de l’ouvrage. En revanche, la zone de modélisation des détails peut être limitée.
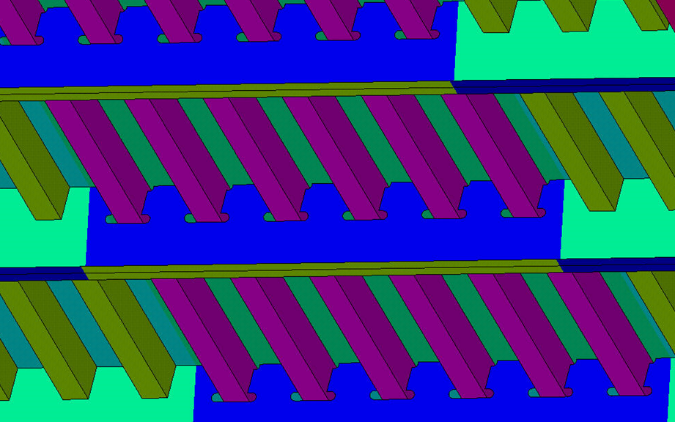
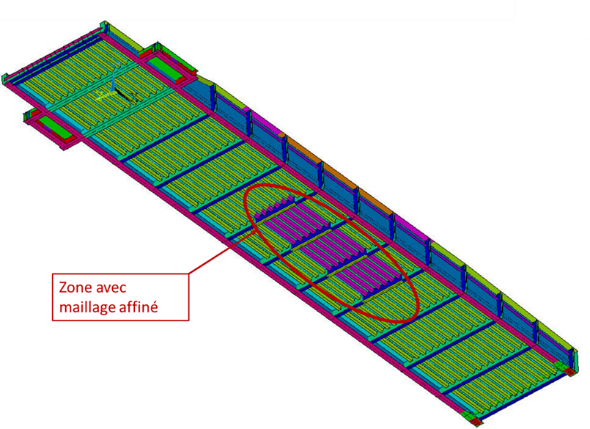
D.6.2 Modélisation – Création du modèle surfacique et maillage
Il convient également de bien appréhender les capacités de maillage du logiciel. La plupart des logiciels peuvent mailler de façon automatique un assemblage de plaques, aussi complexe soit-il.
L’intervention de l’utilisateur peut alors se limiter à la définition de quelques paramètres tels que la taille moyenne des éléments ou leur forme (quadrangulaires, triangulaires). Il vaut mieux cependant avoir la possibilité de pouvoir piloter le maillage en choisissant l’ordre des surfaces à mailler, en venant imposer des tailles de maille plus fines dans certaines zones, ceci afin d’éviter la présence d’éléments dégénérés.
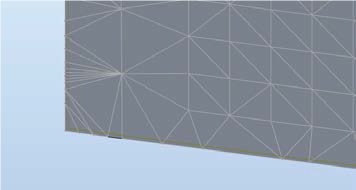
Exemple de maillage dégénéré
Dans un assemblage complexe, du fait de la forme et du nombre de pièces assemblées, le risque de voir se produire des incohérences de maillage est grand. Pour réduire ce risque plusieurs points sont à observer, pour rappel :
-
l’analyse et la perception du fonctionnement RDM de l’assemblage par l’ingénieur au préalable de la modélisation sont fortement conseillées. Certains renforts et certains détails n’ayant qu’un effet très localisé sur le comportement global de l’assemblage peuvent être omis, ce qui permet de réduire le nombre d’interfaces entre plaques ;
-
pour éviter des discontinuités de maillage, toutes les intersections de tôles doivent apparaître. Par exemple dans le cas de la modélisation d’une poutre en I, chacune des semelles apparaîtra composée de deux surfaces identiques de part et d’autre de l’âme. On veillera, au droit de l'intersection de chacune des semelles avec l’âme, à la présence d’une seule ligne commune aux trois surfaces (les deux surfaces constituant la semelle considérée et la surface de l’âme) ;
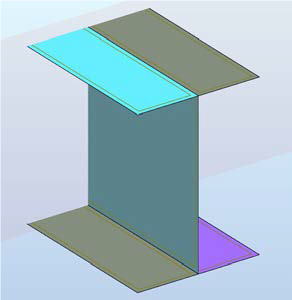
Décomposition en surface élémentaire d’une poutre en I
-
ne pas hésiter à décomposer les surfaces étendues en plusieurs surfaces de forme quadrangulaire, le maillage en sera facilité ainsi que par exemple l'application de charges sous forme de pressions ;
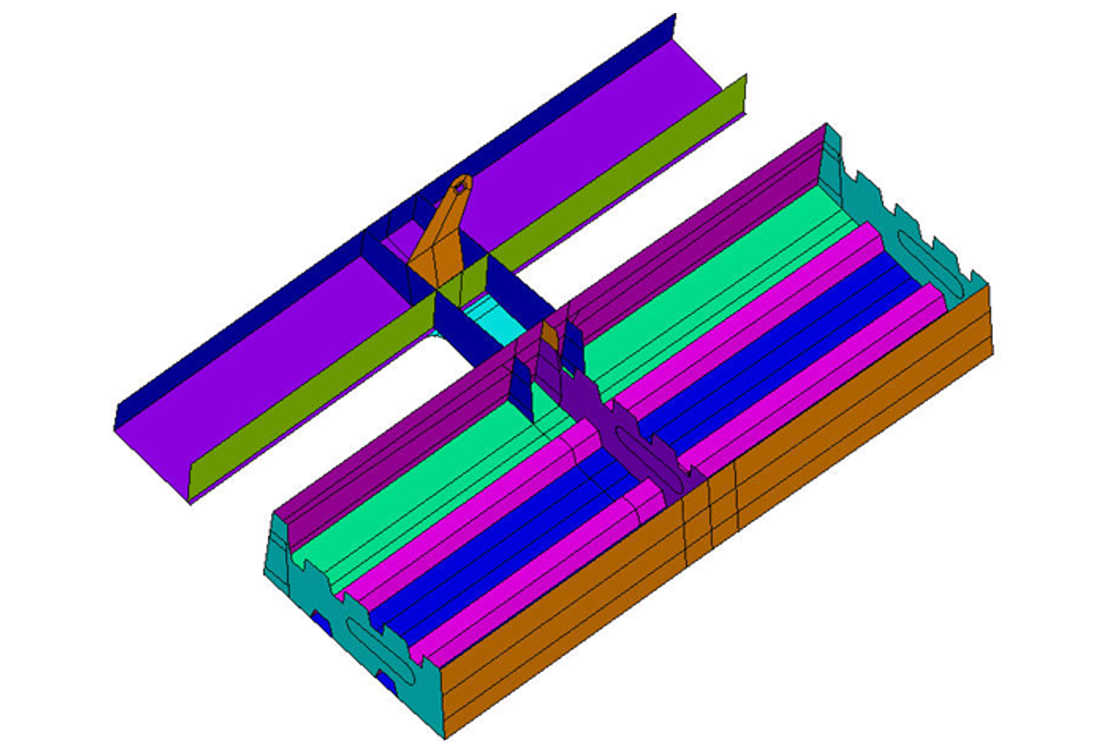
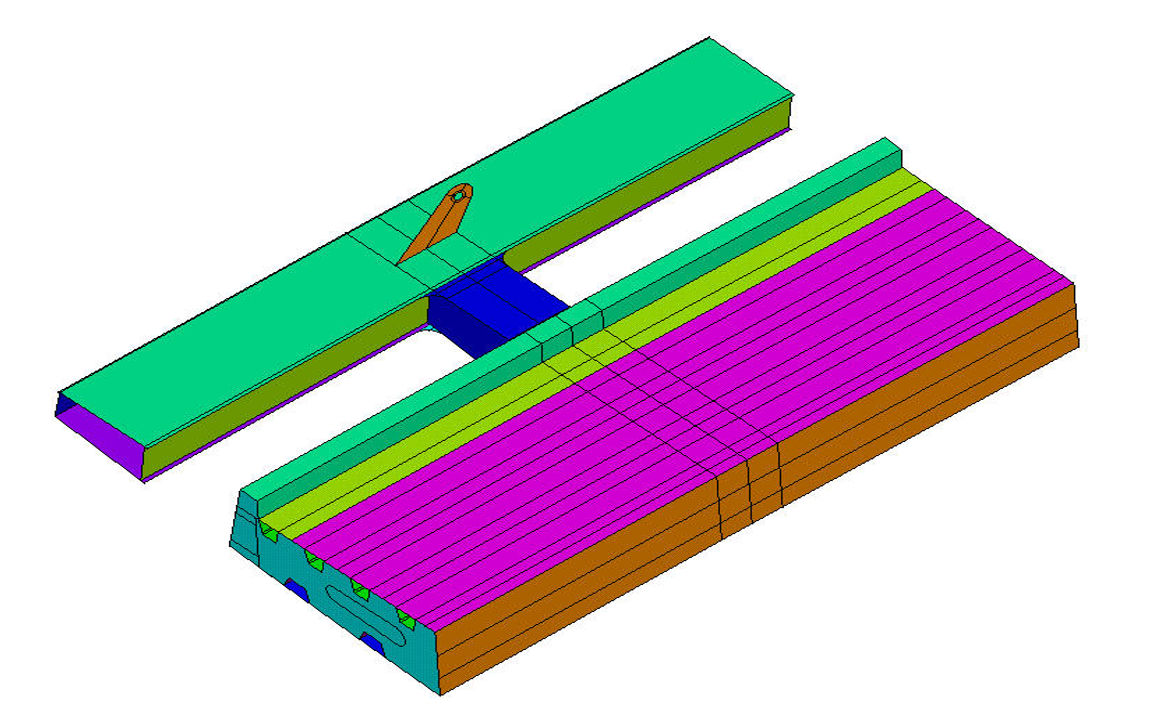
-
La structure de l’ouvrage peut présenter des panneaux ayant une géométrie gauche. Le logiciel peut autoriser la création de surfaces gauches, dans une certaine limite. Par conséquent, selon l’importance du gauchissement, il faudra décomposer le panneau initial en plusieurs sous-panneaux (la frontière commune à deux sous-panneaux étant constituée des mêmes entités). Lors du maillage, les éléments s’appuyant sur une surface gauche présenteront également un gauchissement. Selon les logiciels, la limite du gauchissement admise pour une surface CAO (sur laquelle viendra s’appuyer le maillage des éléments finis) peut être différente de celle admise pour les éléments finis. Dans tous les cas de figure, il est toujours possible d’approximer des éléments gauches à l’aide de surfaces planes triangulaires successives.
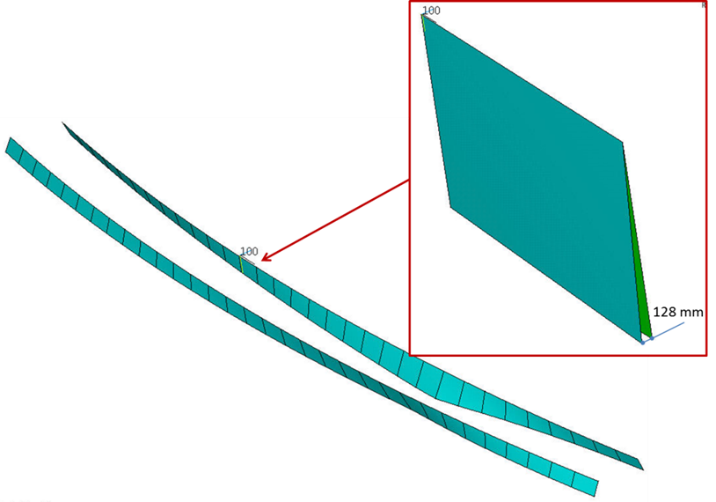
Exemple de panneaux avec des surfaces gauches
-
l’assemblage à modéliser peut présenter des intersections de tubes cylindriques. Si lors du maillage il est fait usage d’éléments sans nœud milieu (éléments à 4 nœuds), le maillage présentera des facettes ; plus la taille des éléments sera grande, plus la taille de ces facettes sera grande. On peut donc réduire cette “facettisation” en augmentant le nombre d’éléments. L’utilisation d’éléments à nœuds milieu peut également être une bonne solution à condition que le logiciel utilisé offre la possibilité aux éléments à nœuds milieu d’épouser la courbure de la surface CAO (ou de la ligne CAO) ;
-
si un tube est connecté à une plaque, attention au niveau de la liaison, à la compatibilité des types d’éléments utilisés (par exemple raccord d’éléments à 4 et à 8 nœuds). On peut dans certains cas obtenir des discontinuités au niveau des résultats (voir § C.6.3) ;
D.6.3 Modélisation – Chargement et conditions aux limites
Une des causes fréquentes de l’apparition de pics de contraintes est la présence d'efforts ponctuels ou de blocages ponctuels.
Si une charge ponctuelle (respectivement un appui ponctuel) mis en place est hors zone d’intérêt, la présence d’un pic de contraintes n’est pas contrariante. En revanche, si elle se trouve dans la zone d’intérêt, plutôt qu’une force ponctuelle, il vaut mieux appliquer la force sur plusieurs nœuds (respectivement bloquer plusieurs nœuds).
Comme décrit dans les chapitres précédents, dans la réalité, les forces ponctuelles et les appuis ponctuels n’ont pas de sens physique (on note néanmoins que dans un modèle de poutre filaire, les appuis ponctuels ne créent pas de pics).
Application pratique :
Considérons une poutre HEB modélisée en éléments de plaques. Un pic de contraintes apparaitrait, si le torseur d’effort dans une section était appliqué en un nœud. Il vaut mieux se rapprocher de la réalité, en transformant le torseur d’effort en contraintes normales et tangentes (sous forme d’efforts linéaires, le cas échéant) et procéder comme suit :
-
l’effort normal sera réparti sur l’ensemble des nœuds de la section d’extrémité ;
-
l’effort tranchant sera réparti sur l’ensemble des nœuds de l’âme de la section d’extrémité ;
-
le moment sera décomposé en deux efforts répartis sur l’ensemble des nœuds des deux semelles de la section d’extrémité.
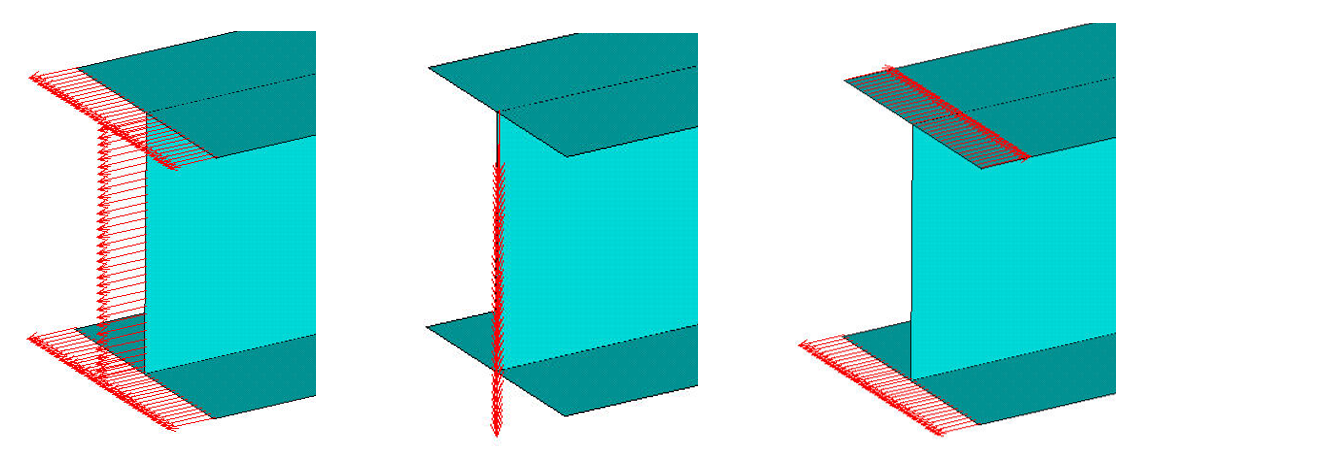
Effort normal / Effort tranchant / Moment fléchissant
Il en sera de même pour modéliser les appuis de la poutre. Considérons les deux cas suivants :
-
poutre de plancher bi-articulée (assemblage par cornières d’âmes aux extrémités) soumise à une charge répartie. On va considérer deux cas se différenciant par la mise en place des conditions aux limites ;

1er cas : en chacune des extrémités, mise en place d'un blocage vertical ponctuel (le blocage transversal de deux nœuds est effectué pour stabiliser la poutre en rotation autour de son axe).
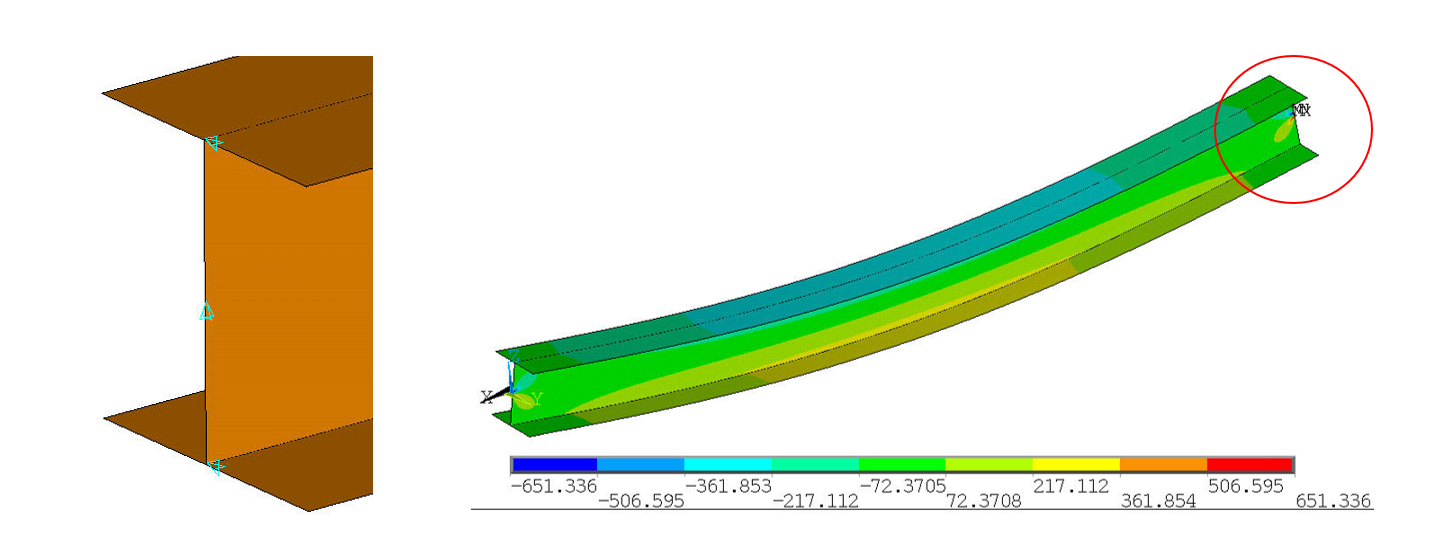
1er cas - conditions aux limites / iso-contraintes longitudinales (en MPa) – la zone du pic de contraintes est entourée
2ème cas : en chacune des extrémités on effectue le blocage vertical et transversal des nœuds d’une partie de l’âme afin de se rapprocher de la réalité.
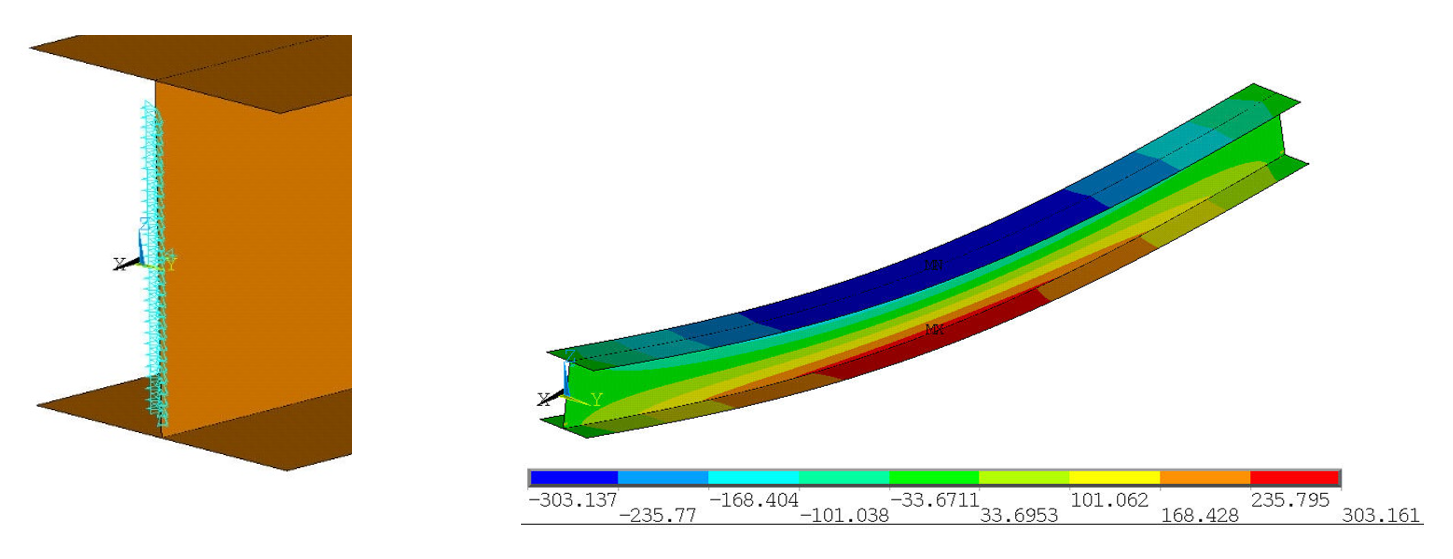
2ème cas - conditions aux limites / iso-contraintes longitudinales (en MPa)
Les pics de contraintes apparaissant dans le 1er cas sont donc dus à la présence d’une réaction nodale ponctuelle. Cependant, en observant les résultats uniquement sur la partie centrale de la poutre, on retrouve des résultats identiques à ceux du 2ème cas.

1er cas – partie centrale – iso-contraintes longitudinales (en MPa)
-
poutre bi-appuyée (appuis sous semelle inférieure) soumise à une charge répartie. Dans un premier temps, on ne modélise que la poutre (de type H) et on applique des conditions aux limites telles que, à proximité de chacune des deux extrémités, les nœuds de la semelle inférieure sont bloqués suivant la direction verticale.
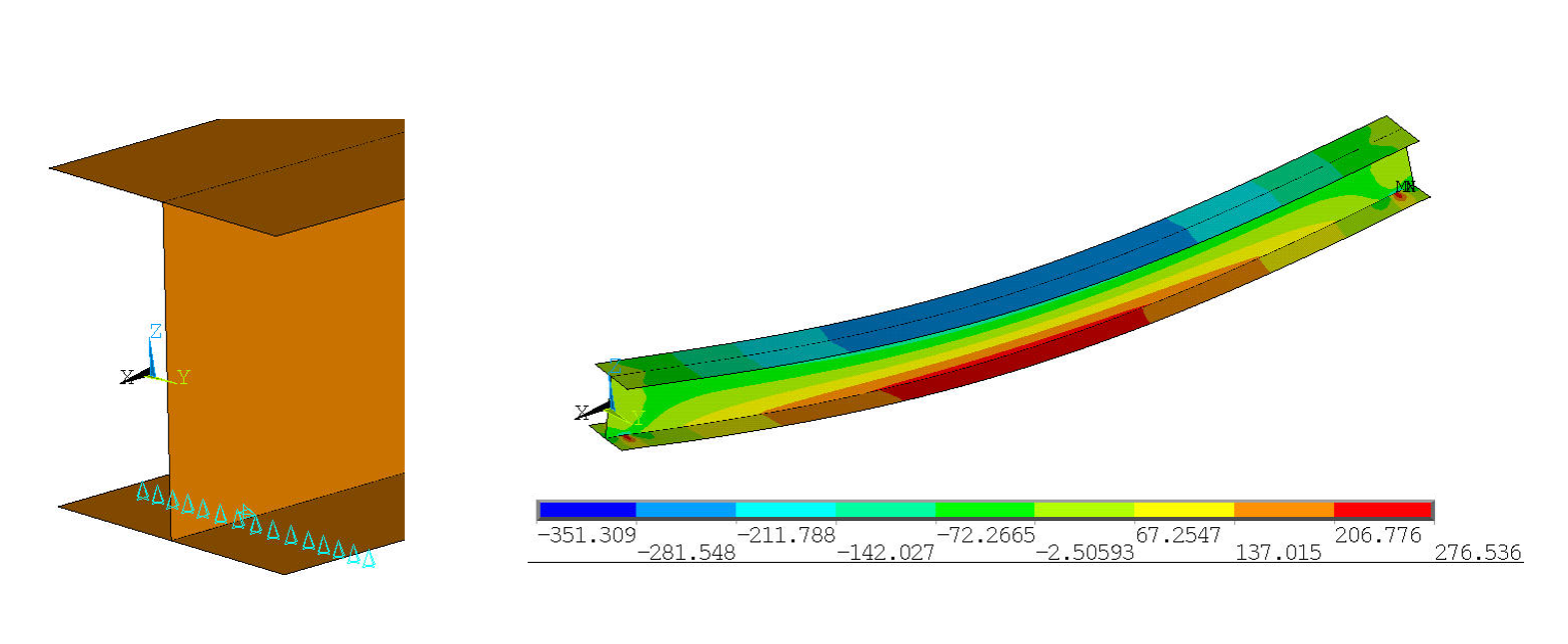
Cas sans raidisseurs - conditions aux limites / Iso-contraintes longitudinales (en MPa)
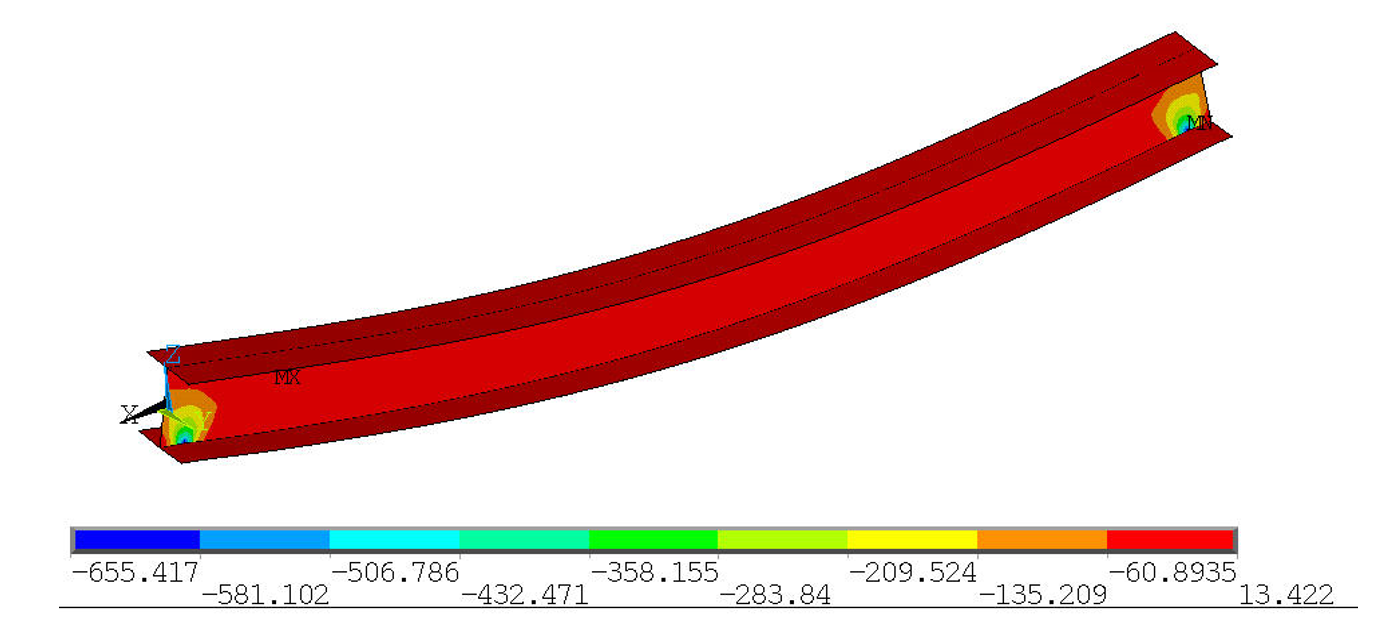
Cas sans raidisseurs - iso-contraintes verticales (en MPa)
Des pointes de contraintes apparaissent à l’intersection âme/semelle inférieure malgré le fait que le blocage vertical ait été effectué sur plusieurs nœuds. Le problème ici est plutôt un problème de conception. Il est d’usage au droit des appuis de mettre en place des raidisseurs transversaux (voir les règlements de calcul concernant la résistance aux forces transversales de l’âme des poutres et les vérifications au voilement local). Si nous reprenons le modèle en ajoutant des raidisseurs transversaux au droit des appuis, les pics de contraintes au droit des appuis disparaissent.
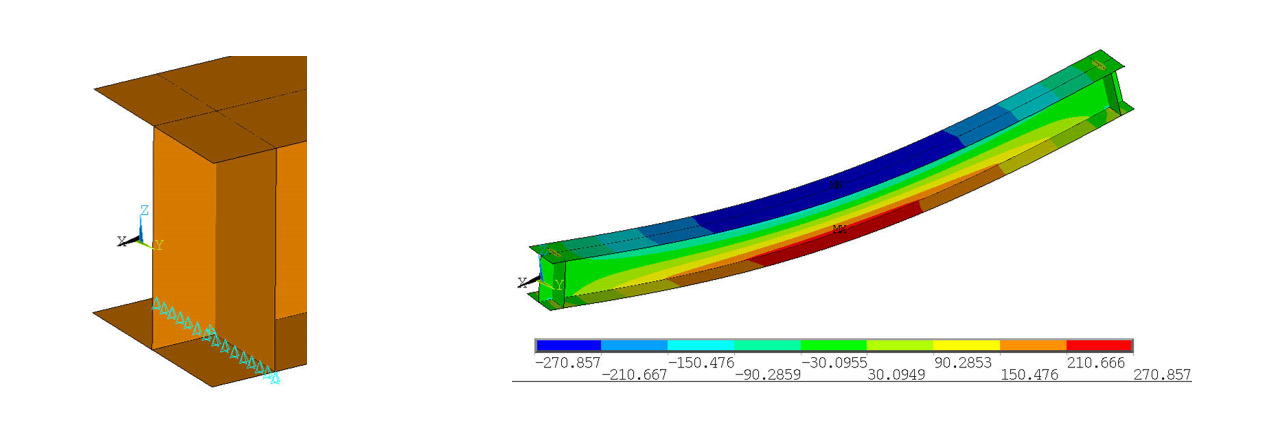
Cas avec raidisseurs - conditions aux limites / iso-contraintes longitudinales (en MPa)
Les pics de contraintes apparaissant en l'absence de raidisseurs sont donc dus à un problème de conception. Cependant, en observant les résultats uniquement sur la partie centrale de la poutre, on retrouve des résultats similaires au cas avec raidisseurs.
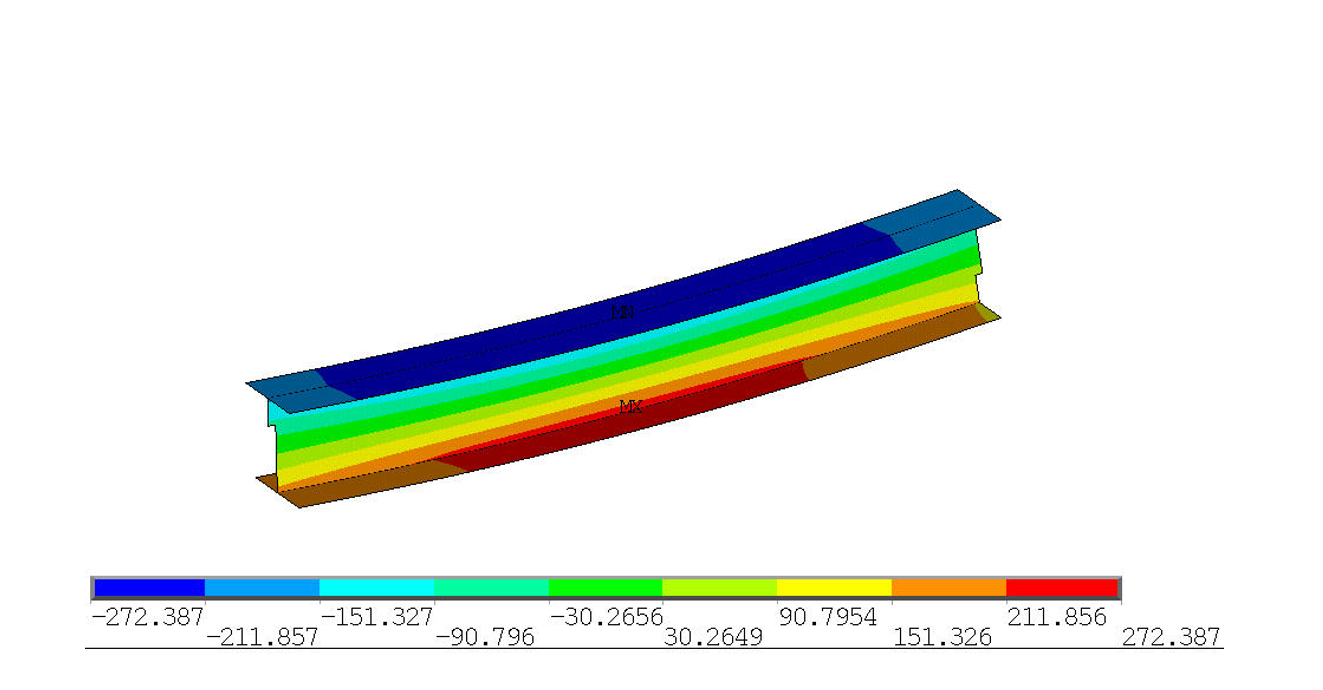
Cas sans raidisseurs – partie centrale – iso-contraintes longitudinales (en MPa)
D.6.4 Analyse des résultats – Validation du modèle
La modélisation étant terminée, en ayant respecté au mieux les conseils énoncés précédemment, le calcul est exécuté. Il convient d’analyser attentivement tous les messages que peut générer le logiciel. Généralement un message d’erreur bloquera le solveur, contrairement aux messages d’avertissement qui devront être analysés et interprétés avec soin. Il est recommandé de ne pas passer outre ces messages sans en avoir bien évalué les conséquences possibles, quitte à mobiliser la hotline de l’éditeur.
Il convient de bien appréhender les capacités offertes par le logiciel pour l’affichage et les types de résultats. Voici une liste non-exhaustive de paramètres au sujet desquels il convient de s’interroger :
-
le repère dans lequel sont affichés les efforts et moments, les déplacements ou les contraintes : s'agit-il du repère global du modèle, des repères locaux des éléments, de repères nodaux? ;
-
les conventions de signe des efforts et contraintes ;
-
la convention utilisée par le logiciel pour la dénomination des forces et moments : par exemple certains logiciels appellent My le moment autour de l’axe Y tandis que, pour d’autres, il correspond au moment parallèle à la direction Y. Ceci est particulièrement vrai lors de l’utilisation de torseurs fournis par un tiers ;
-
les différentes contraintes : contraintes directionnelles, contraintes principales, contraintes équivalentes de Von Mises … ;
-
le type de contraintes affichées et la manière dont elles sont calculées : contraintes aux nœuds ou aux éléments, en surface moyenne ou en peaux ;
-
les possibilités d’extraction des contraintes aux points de Gauss ;
-
la pertinence de l’échelle d’affichage des contraintes qui peut fausser l’interprétation des résultats.
Dans l’exemple ci-dessous, des contraintes largement supérieures à la limite élastique apparaissent sur des pics localisés.
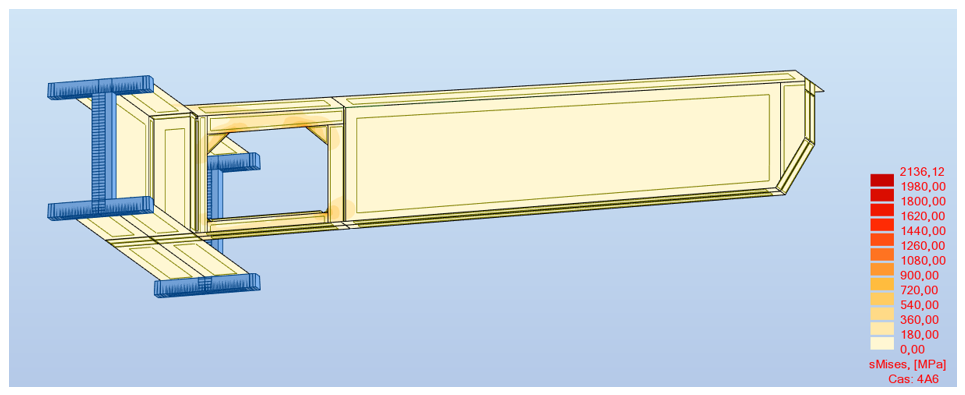
Exemple d'échelle non adaptée à une analyse des contraintes
Un bornage supérieur de l'échelle, possible avec de nombreux logiciels, permet de faire apparaître les zones impactées par les dépassements :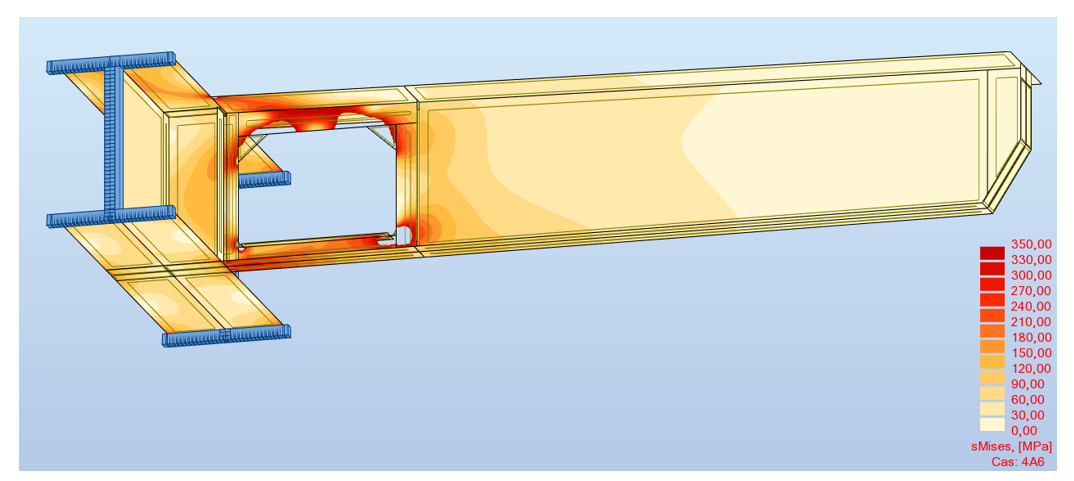
Bornage de l'échelle
Les paramètres d’exploitation du logiciel étant bien appréhendés, avant toute exploitation des résultats et analyse de pics de contraintes subsistant éventuellement, il convient de procéder à quelques vérifications simples pour valider le modèle de calcul :
-
contrôler les descentes de charges (réactions d’appui) afin de s’assurer que l’intégralité des charges introduites se retrouve bien au niveau des appuis déclarés du modèle ;
-
contrôler l’allure de la déformée globale de la structure ;
-
contrôler l’ordre de grandeur des déplacements et leur compatibilité avec les conditions aux limites imposées à la structure et le(s) chargement(s) appliqué(s).
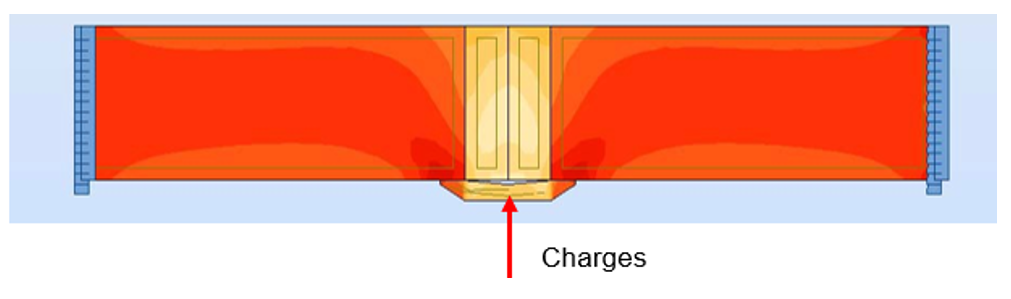
Il s'agit finalement des contrôles fondamentaux qu'il est nécessaire de réaliser pour toute modélisation aux éléments finis (voir le § E.2 Autocontrôle).
D.6.5 Analyse des résultats – Acceptation des pics de contraintes résiduels
Nous l’avons déjà dit, il est possible d'utiliser un modèle présentant des pics de contraintes à condition d’avoir la certitude que ces pics ne perturbent pas le résultat des objectifs de l’étude. En tout état de cause, il appartient à l’ingénieur d’évaluer le caractère gênant ou non d’un pic de contraintes à l’aide de son expérience et de son esprit critique.
-
Zone modélisée sans prise en compte de détails de conception
La mise en place de congés de raccordement ou de raidisseurs locaux a pour but d’assurer entre autres une meilleure diffusion des efforts. Les dispositions constructives et les règles de l’art en matière d’assemblages métalliques vont dans ce sens.
Par conséquent, la non-modélisation d’un détail constructif va probablement se traduire par un pic de contrainte.
Pour autant, la modélisation du détail constructif ne nous exempte pas de la présence d’une concentration de contraintes d’autant plus forte que le maillage de la zone locale du détail est plus grossier. Des tests de sensibilité à la taille des éléments peuvent être réalisés afin de bien appréhender les résultats affichés. Les abaques de concentration de contraintes peuvent également s’avérer utiles.
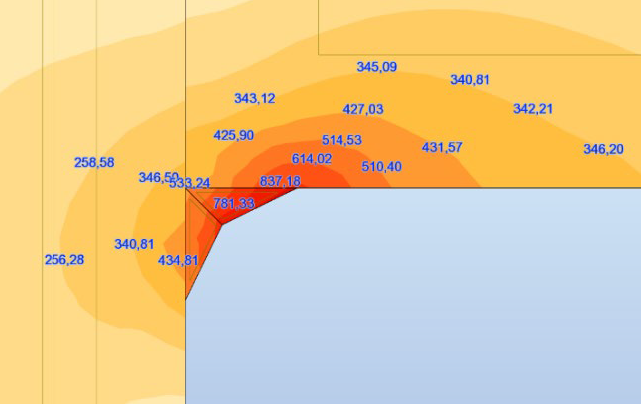
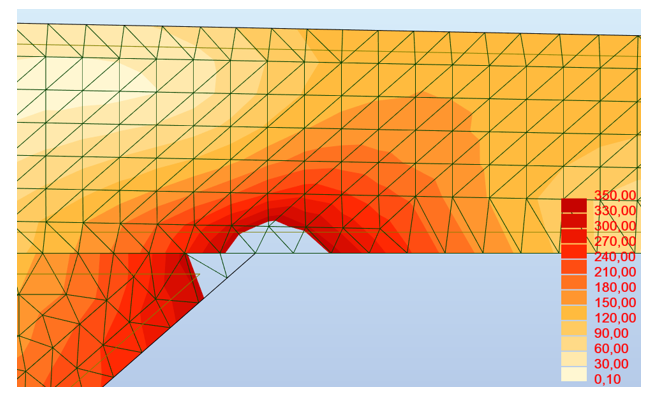
Exemples de concentrations de contraintes au niveau de singularités
Les concentrations de contraintes présentant un pic avec des valeur supérieures à la limite élastique du matériau peuvent être acceptables à l’ELU si elles se trouvent très localisées et en peaux. Néanmoins, leur justification peut nécessiter parfois la réalisation d’un calcul élasto-plastique, surtout si la zone de contraintes dépassant la limite élastique est traversante (risque d’apparition de rotules plastiques). Si le logiciel l’autorise, ce calcul élasto-plastique est réalisé en considérant une loi de comportement bi-linéaire du matériau. L’Annexe C (informative) de l’EN 1993-1-5 autorise une valeur limite de la déformation maximale de 5% pour les zones en traction. Pour les zones en compression, il convient de rester vigilant vis-à-vis des phénomènes de voilement locaux.
-
Zone présentant une singularité de maillage
Le maillage des zones d’intérêt doit être adapté aux champs de contraintes ou de déformations attendues.
Si le maillage est mal adapté avec, par exemple, des changements brusques de taille, des sauts de contraintes d’un élément à l’autre sont à craindre. Une discrétisation défaillante se traduira par des écarts importants entre les résultats de la simulation et la réalité. Ces écarts peuvent être réduits en procédant à une étude de sensibilité du maillage : on estime que le maillage est satisfaisant lorsque le raffinement entraîne une variation faible du résultat ; par exemple une variation inférieure à 5% pour des tailles d’éléments divisées par 2). Mais attention, ce n’est pas parce qu’un résultat semble stabilisé à 5% que l’on approche la réalité à 5%.
Il n’est pas nécessaire de raffiner le maillage sur la totalité du modèle. La plupart des logiciels permettent d’afficher des cartes d’erreur permettant de localiser les zones à fort saut de contrainte. Certains logiciels permettent même de corriger automatiquement le maillage afin de réduire ces écarts (maillage adaptatif).
-
Zone avec effort ponctuel ou blocage ponctuel
Nous avons présenté précédemment les effets de la mise en place d’un effort ou d’un blocage ponctuel.
Cependant, même en ayant pris le soin de répartir la charge sur plusieurs nœuds, il se peut que des concentrations de contraintes apparaissent avec des valeurs maximales supérieures à la limite élastique du matériau. Cette situation peut néanmoins être tout à fait admissible selon l’objectif de l’étude et de la modélisation. Prenons le cas, par exemple, de la modélisation de la zone d’attache d’une suspente. L’effort provenant de la suspente est réparti suivant une répartition sinusoïdale sur les nœuds de la moitié de la circonférence de l’alésage (trou).
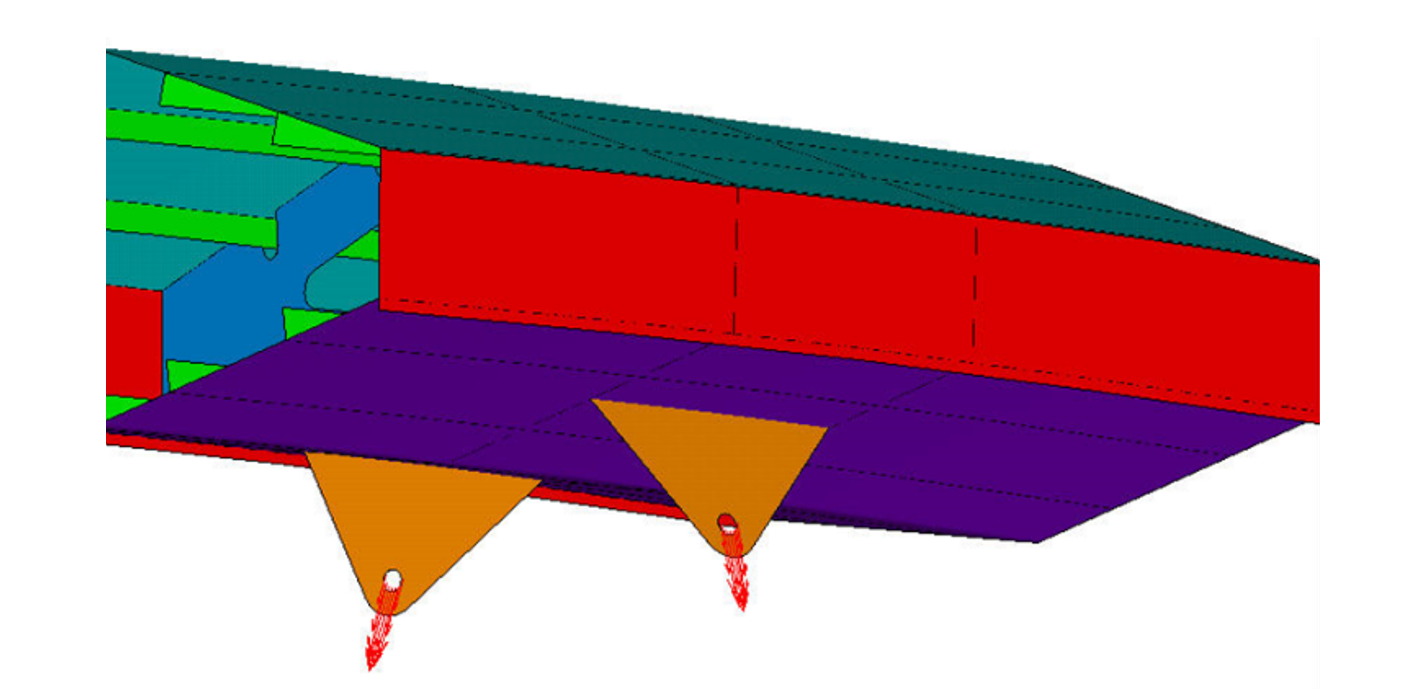
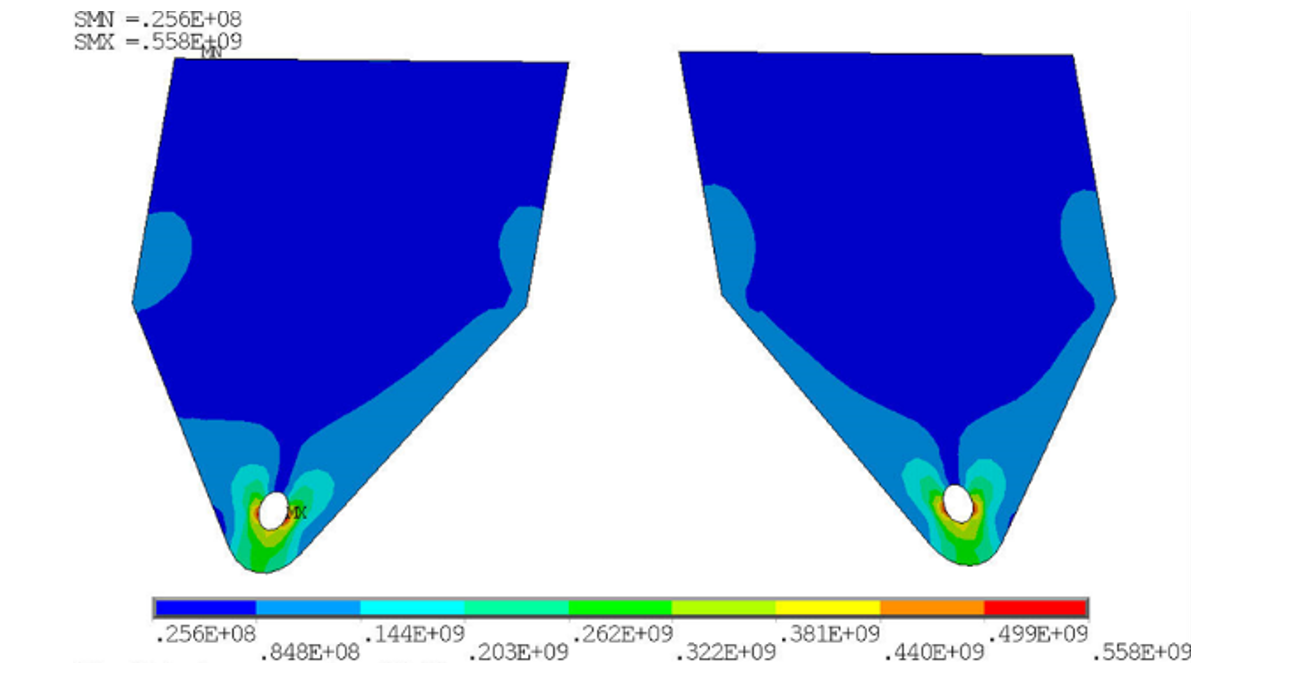
Nous obtenons une concentration de contraintes autour des alésages des axes dont la valeur maximale est de 558 MPa, valeur bien au-delà de la limite élastique de 400 MPa. Cependant, cette valeur maximale n’est pas à comparer à la limite élastique. La concentration de contraintes est due ici à la pression diamétrale et les règlements indiquent que la résistance en pression diamétrale de la plaque est égale à 1,5.t.d.fy. L’épaisseur t de la chape et le diamètre d de l’alésage étant pris en compte de par la modélisation, il convient donc comparer 558 MPa à 1,5 x 400 = 600 MPa.
D.6.6 Synthèse
Si les pics de contraintes sont dus à des singularités (angle rentrant, interface entre deux matériaux différents, efforts ponctuels), ils peuvent être négligés … si l’état de contraintes au voisinage de la singularité ne fait pas partie des objectifs de l’étude EF. Sinon, il convient d’améliorer la modélisation (remplacer l’angle entrant par un congé de raccordement, remplacer la zone de discontinuité entre lois de comportement de matériaux différentes par une zone de transition dans laquelle les paramètres varient de façon continus, remplacer une force ponctuelle par une pression de contact sur une surface non nulle).
Si ces pics de contrainte apparaissent dans des zones hors voisinage d’une singularité, il convient de prendre la peine de raffiner successivement le maillage de ces zones pour connaître le niveau de contraintes plus réaliste.
Concernant le lissage, il n’y pas de méthode simple et directe. Le lecteur pourra regarder ce qui est pratiqué pour les calculs en fatigue, dans le cas d’un gradient de contraintes important au voisinage du pied de cordon de soudure dans les assemblages, avec l’application de la méthode de la contrainte géométrique au point chaud (voir la bibliographie (réf. Hobbacher)).
Concernant la valeur de la contrainte maximale obtenue, elle doit être comparée à la valeur limite précisée par les Normes de Calcul. Pour les aciers, les normes Eurocodes définissent la valeur de la limite élastique selon la nuance de l’acier et l’épaisseur de la plaque ou du tube ; par exemple pour un tube en acier S355 d’épaisseur 35 mm → limite élastique = 345 MPa selon l’EN 10210.
Tout dépassement de cette limite :
-
doit donc être justifié. Et cela peut être paradoxal, mais on aura plus de facilité pour justifier un dépassement de contraintes au droit d’une singularité qu'en zone courante;
-
doit être également acceptable. En cas de dépassement de la limite élastique, une plastification apparaîtra. Un calcul élasto-plastique donnera une information sur la taux de déformation (pour les aciers de construction, l’Eurocode EN 1993-1-5 spécifie une limite de déformation principale maximale de 5%). La norme précise les critères relatifs à l’ELU qui peuvent être utilisés. Pour les zones en traction, il s'agit de l'atteinte d’une valeur limite de la déformation de membrane principale (limite de 5% recommandée) et pour les structures sensibles aux phénomènes de voilement, l'atteinte de la charge maximale.
Rappelons, enfin, qu'un calcul EF (sauf à activer certaines options de calcul très spécifiques) ne permet pas de tenir compte de phénomènes autres que le traînage de cisaillement, par exemple les phénomènes d’instabilité tels que le voilement et le déversement des tôles.
Application numérique : Illustration du chapitre D.6 - Pics dans les angles, incidence du maillage et des congés. Lien vers le fichier.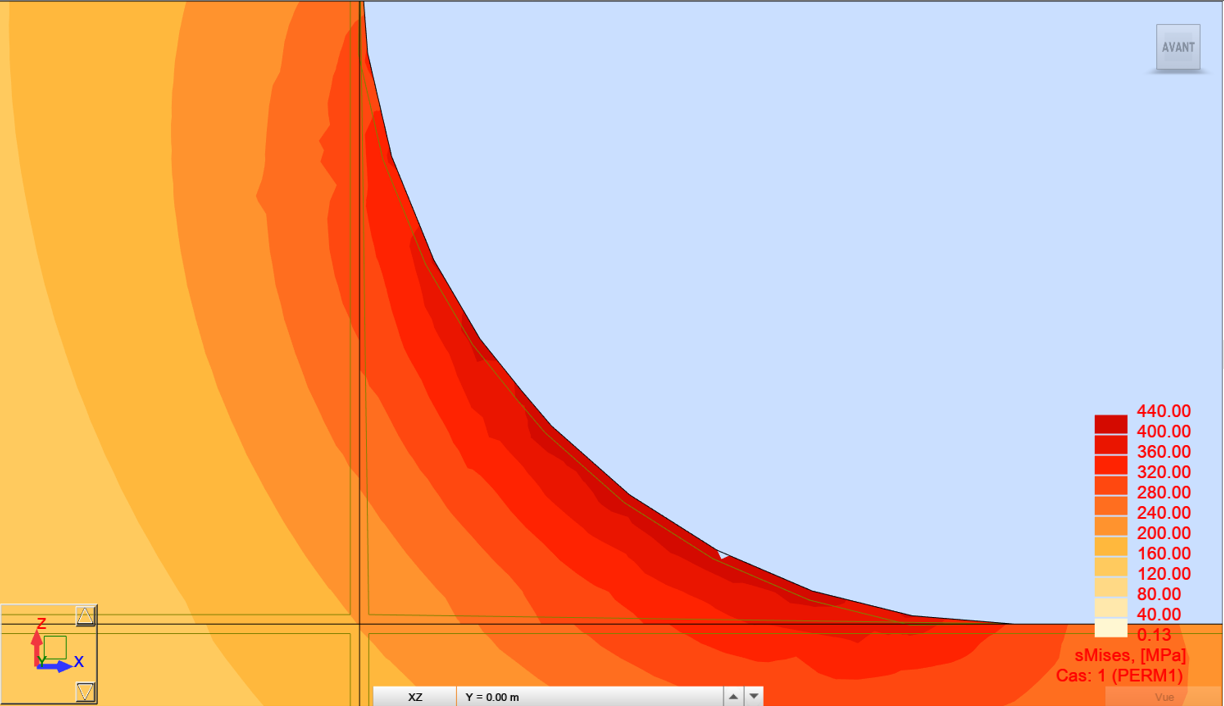
D.7 Compléments spécifiques pour les calculs dynamiques
D.7 Compléments spécifiques pour les calculs dynamiques
D.7.1 Vérification de la masse totale
Dans le cas d’études de type dynamique, l’un des paramètres fondamentaux est la masse de la structure qui sert à déterminer les fréquences propres de celle-ci.
Il est ainsi très important de s’assurer que l’intégralité de la masse de la structure est effectivement entrée dans le modèle. En effet, dans le cas où l’on utilise un modèle qui a déjà servi pour des calculs statiques, il peut arriver que certaines charges permanentes ou variables, telles que des équipements, aient été entrées en tant que charges (ponctuelles, linéaires, surfaciques, etc.) et non en tant que masse. Dès lors, il peut arriver que le programme ne considère pas ces charges comme masses mais uniquement comme des surcharges, et ne les prenne pas en compte dans son calcul de masse. Ceci risque de minorer les efforts sismiques.
Il convient donc de toujours s’assurer que la masse totale de la structure est bien celle recherchée. Cette information est en général accessible dans les résultats de l’analyse modale ou, encore mieux, peut être obtenue en effectuant trois calculs statiques, en appliquant un champ d’accélération unitaire dans les 3 directions (X,Y,Z) : seuls les éléments ayant une masse seront donc pris en compte, et la somme des réactions permettra donc de connaître la masse réellement prise en compte dans le modèle, dans chaque direction.
D.7.2 Vérification des masses participantes
Il convient de vérifier que l’analyse modale effectuée prend en compte suffisamment de modes propres. Pour cela, il faut vérifier que les masses modales participantes dans la direction étudiée et cumulées pour les différents modes calculés, représentent au moins 90% de la masse totale pouvant être mise en mouvement, calculée à partir des cas unitaires d’accélération, sans quoi les normes autorisent la prise en compte d’un pseudo mode (par direction).
Piège : Certains logiciels indiquent des % de masse modales cumulées qui peuvent être basés sur une mauvaise hypothèses de masse totale mobilisée : en effet, les parties de masses bloquées en déplacement par des appuis ne seront pas comptabilisées par le logiciel qui sur-évaluera de ce fait le % modal mobilisé. Une astuce pour pallier ceci est de définir des appuis élastiques avec une forte raideur plutôt que des appuis fixes : la masse totale sera alors exacte.
De manière générale, il est préférable de ne pas modéliser de masse associée à des appuis fixes.
Exemple de l’étude d’un modèle brochette avec 5 degrés de liberté :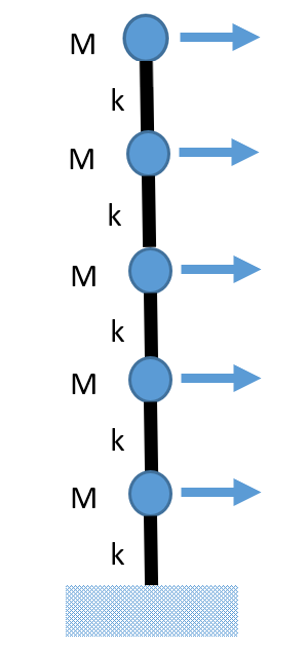
Trois cas sont étudiés :
-
Cas 1 : Masses et raideurs similaires à tous les niveaux ;
-
Cas 2 : Cas 1 mais avec une raideur 100 fois supérieure dans la hauteur du rez-de-chaussée ;
-
Cas 3 : Cas 1 mais avec une raideur 100 fois supérieure dans la hauteur des 2 premiers étages.
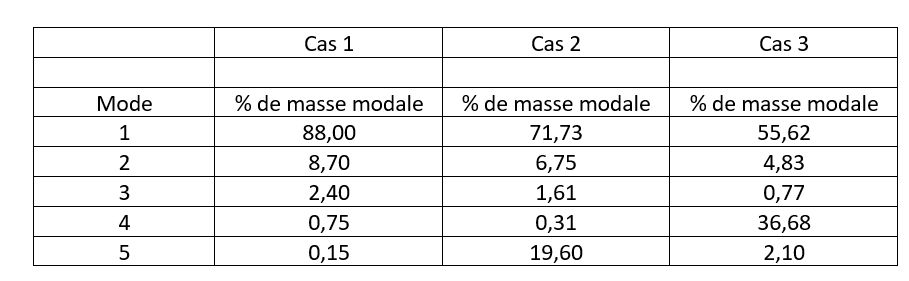
En supposant que toutes les périodes correspondent au plateau du spectre (valeur spectrale identique pour toutes les périodes) :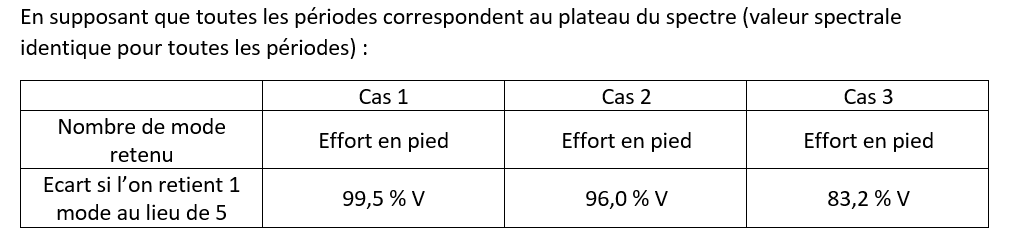
Il est donc important de prendre en compte tous les modes significatifs sinon les efforts de calculs pourraient être notablement sous-estimés.
Piège: Modes symétriques et antisymétriques.
Exemple de vibration d'une poutre
Suivant le type de calcul que l'on effectue, il ne faut pas considérer que les modes qui n'apportent pas de supplément de % de masse modale dans une direction donnée sont forcément sans intérêt.
Cas simple de la poutre sur deux appuis - les masses ne sont mobilisées que verticalement. Le tableau des résultats modaux montre que tous les modes pairs n'apportent pas de supplément de % de masse modale.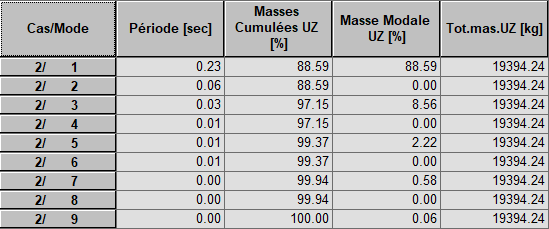
En examinant les déformées modales, on se rend compte que ce sont des modes ayant des déformées antisymétriques:
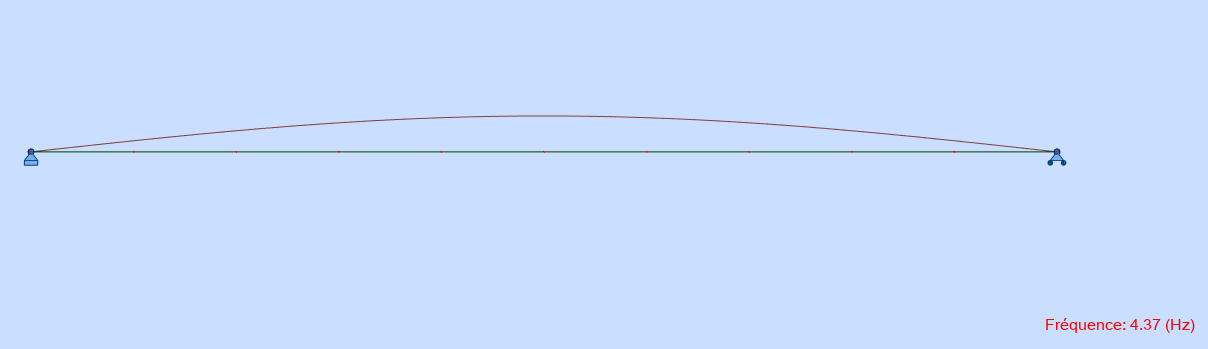
Déformée modale - mode 1
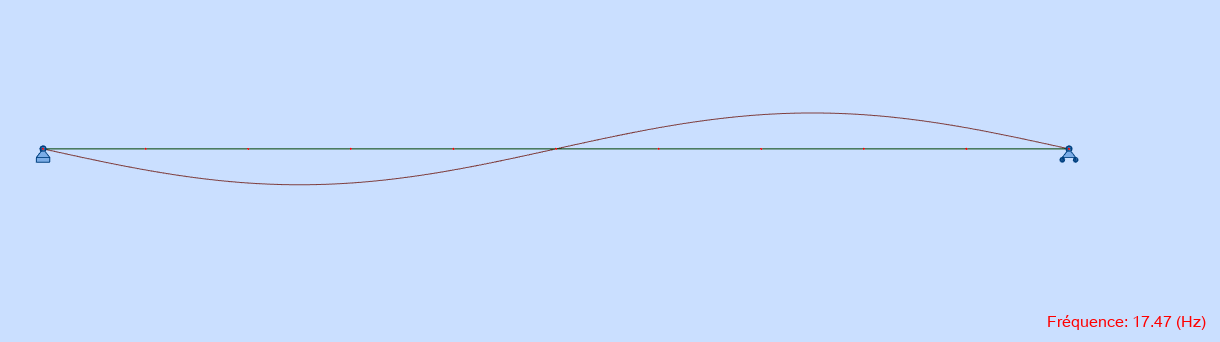
Déformée modale - mode 2
Dans le cas d'un calcul sismique spectral, ces modes n'apportent effectivement rien, par contre dans le cas d'un calcul de vibration d'une poutre ou d'une passerelle, ces modes ont tout leur intérêt. On admet effectivement que des piétons, dans leur mouvements peuvent avoir des actions en opposition et dans le sens la déformée modale. Un calcul harmonique est en effet effectué à partir des charges positionnées tel que ci-après: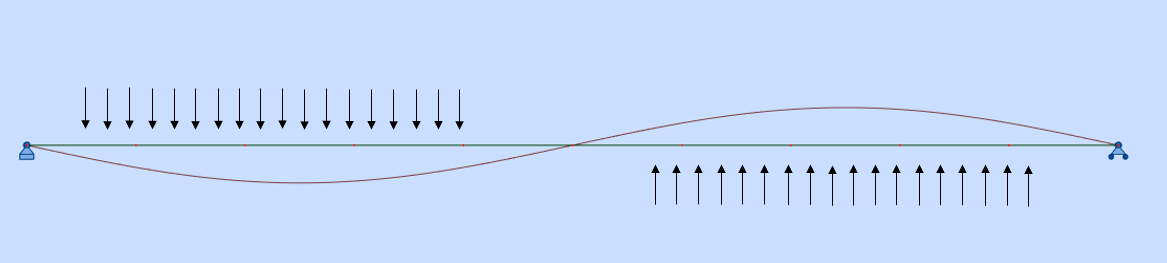
On se référera utilement au guide du Sétra/Cerema sur les passerelles piétonnes pour plus d'informations.
Analyse spectrale: enfin, on donne ci-dessous les efforts au nœud médian de cette poutre, calculée par une analyse sismique spectrale - on constate que les modes pairs n'amènent effectivement aucune contribution.
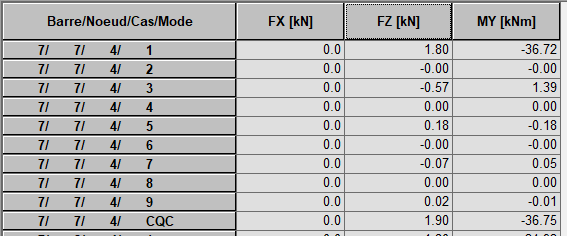
Piège: Modes de torsion
Exemple d'un bâtiment en torsion
Généralement, les bâtiments courants présentent un mode de torsion. Sur l’exemple ci-dessous, on peut observer :
-
Le 1er mode : avec un mode prépondérant selon UY (longitudinal),
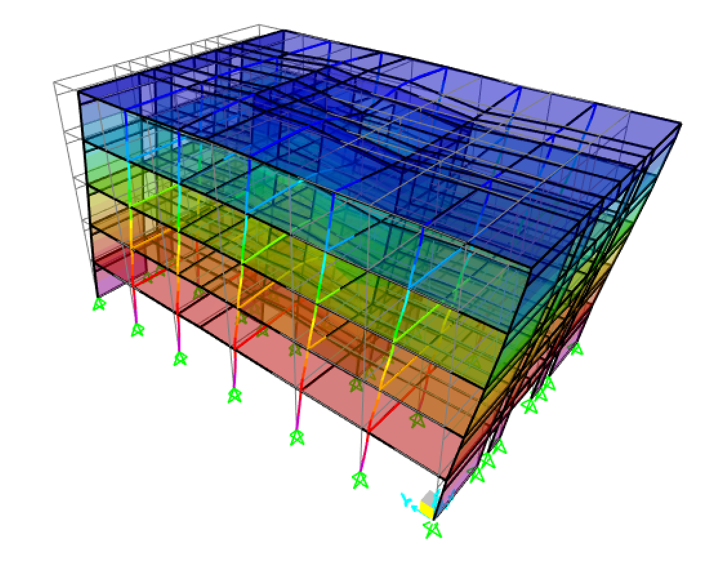
-
Le 2ème mode : avec un mode prépondérant selon UX (transversal),
-
Le 3ème mode : avec peu de participation modale alors qu’il affecte notablement la structure. Il s'agit d'un mode de torsion.

D.7.3 Vérification des principales fréquences propres
Afin de vérifier le comportement effectif de la structure en dynamique, il convient de s’assurer que les principales fréquences propres de la structure ont un ordre de grandeur cohérent.
Ces fréquences correspondent aux principaux modes de flexion, torsion, cisaillement, et elles correspondent en général aux modes ayant des facteurs de participation et des masses participantes importantes.
On notera néanmoins que se limiter aux modes ayant un facteur de participation important n’est pas un garant exhaustif des modes pouvant poser problème sous chargement dynamique. En effet, les facteurs de participation peuvent être calculés par les logiciels sur la base des déplacements modaux signés. Ainsi, il peut arriver que les facteurs de participation prenant en compte le cumul des valeurs renvoient des valeurs faibles alors que le mode est important.
Cela peut arriver par exemple pour une poutre continue sur trois appuis identiques et ayant deux portées identiques. Le principal mode de flexion de cette poutre correspond à la flexion d’une travée dans un sens et à la flexion de l’autre travée dans l’autre sens (forme de vague). Le facteur de participation de ce mode peut être très faible, les déplacements d’une travée contrebalançant les déplacements de l’autre travée dans le calcul, alors que ce mode est le principal mode de flexion de la structure, et peut être celui donnant la réponse en accélération la plus élevée si la structure est soumise à une excitation périodique.
Lorsque la structure est complexe, les formules de dynamique données dans la littérature ne permettent pas de retrouver précisément les valeurs de fréquence propre obtenues, puisque ces formules concernent des structures simples (fréquence propre d’une poutre isostatique sur deux appuis, d’une poutre en console, d’une poutre bi-encastrée ou d’un oscillateur à quelques degrés de libertés). Cependant, ces formules classiques permettent d’estimer les ordres de grandeur des principales fréquences propres en estimant de manière simplifiée le comportement de la structure pour se ramener à des fonctionnements simples pour les vérifications.
Dans le cas de structure de type poutre, on pourra ainsi estimer les fréquences propres de flexion à partir des formules classiques. Par exemple, et de manière très large, la fréquence propre de flexion d’une poutre sur deux appuis ayant une souplesse en rotation sera comprise entre la fréquence propre de flexion de la même poutre mais sur appuis rotulés et la fréquence propre de flexion de la même poutre sur appuis encastrés.
D.7.4 Calculs dynamiques sismiques modal/spectral
D.7.4.1 Vérification de la pertinence des premiers modes (instabilités, déplacements)
Les 2 ou 3 premiers modes globaux visualisent le fonctionnement de la structure, ce qui permet d’une part d’en comprendre le fonctionnement, d’autre part de repérer les problèmes de modélisation.
Pour un bâtiment bien dimensionné, les 2 premiers modes sont toujours selon X et Y, le troisième mode est un mode de torsion.
Pour les bâtiments courants, la période fondamentale est de l'ordre de 1/25 à 1/16 du nombre d'étages.
D.7.4.2 Vérification des axes globaux X et Y par rapport aux premiers modes
Il faut vérifier que les directions sismiques étudiées X et Y sont alignées selon les premiers modes importants. Dans le cas contraire, les calculs des CQC seront faussés.
Les solutions sont :
-
dans le cas d’un bâtiment, tourner le modèle selon les axes principaux
-
dans le cas d’un pont courbe, soit calculer le séisme sur un modèle droit, soit faire plusieurs calculs en variant les axes en fonction des biais des piles.
D.7.4.3 Validation du nombre de modes - Mode complémentaire
L’Eurocode 8 fixe un pourcentage minimum de masse à intéresser dans le calcul spectral.
Si l’on n’arrive pas à intéresser 90% de la masse, les logiciels permettent la prise en compte d’un mode complémentaire. C’est un mode fictif affecté de la masse non excitée par les modes étudiés et affecté de l’accélération spectrale associé au dernier mode étudié.
On a pu voir que négliger des modes fausse les résultats (cf. 1er exemple du D.7.2).
D.7.4.4 Calcul spectral et combinaisons CQC
Le calcul spectral permet d'obtenir les effets structurels (efforts, déplacements…) de chacun des modes. Puis, en fonction de la répartition statistique du séisme suivant les fréquences (définie par le spectre réglementaire), les effets sont combinés de manière à obtenir la réponse statistique de la structure à un séisme.
La combinaison des différents calculs modaux unitaires se fait selon le mode CQC ou SRSS, dont la définition théorique est fournie en Partie 1 – Chapitre 2.
Il convient de distinguer les spectres règlementaires utilisés en bâtiment (qui sont généralement des spectres de dimensionnement) et ceux utilisés pour les ponts (qui sont des spectres élastiques).
On passe du second au premier en divisant par un coefficient de comportement (égal ou supérieur à 1,5) qui tient compte des capacités de plastification de la structure. Les valeurs des coefficients de comportement sont définis par l'Eurocode 8.
Dans tous les calculs spectraux, il convient de veiller à bien définir l’amortissement de la structure. Selon les logiciels, on affecte l’amortissement aux modes ou aux matériaux. Dans le second cas, l’amortissement du mode dépendra de la participation de chaque matériau dans la déformée du mode considéré.
Attention, si l'on souhaite attribuer un amortissement dans les ressorts modélisant le sol, ceci correspond à une étude de type interaction sol-structure dynamique, et il n'est pas possible d'utiliser un spectre de dimensionnement mais uniquement un spectre élastique.
Enfin, comme indiqué en C16.8, un coefficient de comportement différent peut être affecté à chaque direction.
Après les combinaisons CQC ou SRSS (qui combinent les modes), il faut faire les combinaisons de Newmark (combinaisons de direction de séisme), puis les combinaisons d'actions.
D.7.4.5 Vérification des réactions d’appuis sous cas élémentaires
Il faut dans un premier temps faire le bilan des réactions d’appuis des cas sismiques élémentaires EX EY EZ et les comparer aux masses totales.
La vérification des réactions d’appuis ne peut se faire qu’en signant les modes.
Pour un bâtiment fondé sur radier ou sur semelles filantes, il est important de limiter les décollements des appuis, en effet le calcul élastique fait apparaitre des tractions dans les appuis qui n’existent pas dans la réalité car les fondations se soulèvent.
Les réactions d’appuis négatives (entourées en rouge) ne peuvent pas exister car les fondations se soulèvent dans la réalité, la répartition réelle des contraintes sur le sol est donc différente de celle calculée (cf. C16.8.3).
Réactions d’appuis d’un bâtiment sous fondations superficielles
Il est admis de considérer les modélisations « élastiques » représentatives si les soulèvements sont limités : la limite est prise égale à 30% dans le cas général (voire 10% dans le cas de bâtiment nucléaire)
Lorsque les décollements sont importants, il faut procéder à des calculs sismiques non-linéaires beaucoup plus complexes. Cette vérification de non soulèvement du bâtiment doit être réalisée avec soin :
-
il est nécessaire de signer les modes en fonction des modes principaux car les réactions d’appuis CQC sont toujours positives.
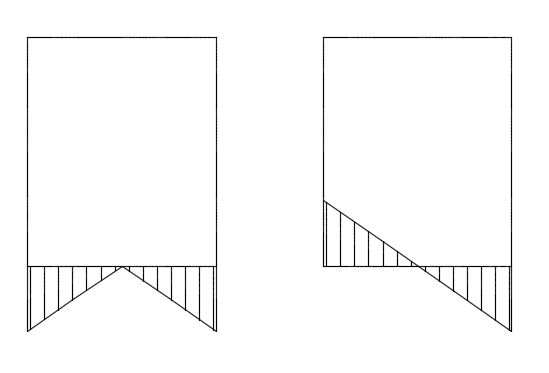
Réactions d’appuis CQC / Réactions d’appuis CQC signées
Les combinaisons sismiques (CP + E) n’ont aucun sens si les efforts sismiques E sont tous positifs, alors que les charges permanentes CP sont soit positives soit négatives.
-
Il est nécessaire d’étudier séparément toutes les combinaisons de Newmark
Exemple des 24 combinaisons de Newmark pour le bâti courant :
-
CP +/- 1.0 EX +/- 0.3 EY +/- 0.3 EZ
-
CP +/- 0.3 EX +/- 1.0 EY +/- 0.3 EZ
-
CP +/- 0.3 EX +/- 0.3 EY +/- 1.0 EZ
D.7.5 Calculs dynamiques autres que sismiques
Ce paragraphe concerne les calculs dynamiques autres que des calculs modaux spectraux (par exemple vibration d’un ouvrage ferroviaire ou d’une passerelle piétonne en vue de vérifier des critères de confort), et correspond à des calculs dans lesquels le chargement et la structure sont calculés avec une évolution dans le temps.
D.7.5.1 Vérification du comportement en vibrations libres ou à la résonance
Dans le cas d’une étude de confort d’un ouvrage ferroviaire ou d’une passerelle, il convient de rechercher les cas de charges pouvant provoquer une mise en résonance de la structure et les conséquences d’une telle mise en résonance. Pour cela, il est donc nécessaire d’appliquer des chargements périodiques pouvant provoquer ces mises en résonances.
Pour rappel, la résonance de la structure intervient quand le chargement périodique est à une fréquence identique à l’une des fréquences propres de la structure.
Pour vérifier que les fréquences des chargements périodiques appliqués sont cohérentes avec celles de la structure, on peut aisément les retrouver sur les graphiques temporels obtenus a posteriori. Cette méthode s’applique sur l’évolution temporelle de l’accélération, de la vitesse ou du déplacement d’un nœud représentatif (par exemple le milieu d’une poutre).
Pour cela, il suffit d’effectuer un décompte du nombre de périodes entre deux points éloignés dans le temps et de diviser ce nombre par le temps séparant ces deux points. Cela donne une assez bonne approximation de la fréquence de vibration du nœud en question:
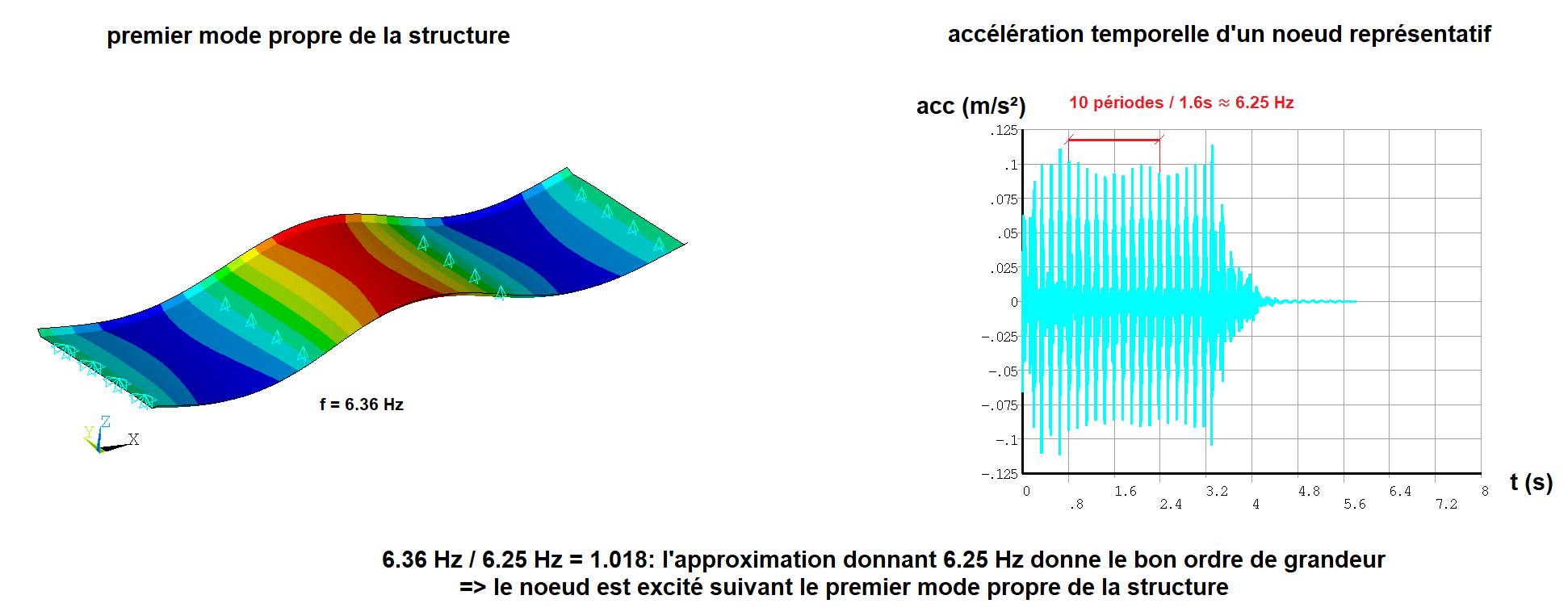
Si la courbe présente une variation périodique très marquée sur la période de temps où le chargement est appliqué, cela correspond à une vibration forcée de la structure, et la méthode décrite précédemment permet de s’assurer que la fréquence du chargement est bien celle attendue.
Si la courbe présente cette variation périodique sur un laps de temps postérieur au chargement (le calcul a été continué après avoir cessé d’appliquer le chargement), cela correspond aux vibrations libres de la structure. La méthode décrite précédemment permet, dans ce cas d’estimer, la principale fréquence propre de la structure et donc de s’assurer que le mode propre excité est bien le bon.
$translationBooksChapitre E. Comment assurer la qualité ?
Chapitre E. Comment assurer la qualité ?
Nous proposons ci-dessous quelques conseils simples pour déployer une démarche qualité dans les calculs aux éléments finis. Les enjeux principaux sont :
-
La bonne utilisation du logiciel
-
La modélisation appropriée du comportement des structures
-
La traçabilité des hypothèses de modélisation et des résultats.
Les conseils ci-dessous traitent de la bonne prise en main d’un logiciel par un ingénieur ou une équipe, des tests d’autocontrôle que doit impérativement effectuer chaque ingénieur à la fin de sa modélisation, et enfin des éléments minimaux à tracer pour permettre le travail à plusieurs ou la reprise ultérieure d’un modèle.
E.1 Prise en main d’un nouveau logiciel
E.2 Validation d’un modèle par autocontrôle
E.3 Traçabilité et travail à plusieurs
$translationBooksE.1 Prise en main d’un nouveau logiciel
E.1 Prise en main d’un nouveau logiciel
Nous proposons ci-dessous quelques conseils simples pour déployer une démarche qualité dans les calculs aux éléments finis. Les enjeux principaux sont :
-
la bonne utilisation du logiciel ;
-
la modélisation appropriée du comportement des structures ;
-
la traçabilité des hypothèses de modélisation et des résultats.
Les conseils ci-dessous traitent de la bonne prise en main d’un logiciel par un ingénieur ou une équipe, des tests d’autocontrôle que doit impérativement effectuer chaque ingénieur à la fin de sa modélisation, et enfin des éléments minimaux à tracer pour permettre le travail à plusieurs ou la reprise ultérieure d’un modèle.
E.1 Prise en main d’un nouveau logiciel
Lors de l’achat d’un nouveau logiciel au sein d’un bureau d’études, ou à l’occasion de l’arrivée de nouveaux ingénieurs, il y a une étape très importante - et malheureusement souvent négligée – celle de l’appropriation du logiciel et de la validation du couple utilisateur-logiciel.
Cette validation, à placer sous le responsabilité du management, est au cœur de la démarche qualité des études qui seront produites. On a vu, dans les paragraphes précédents, toutes les erreurs possibles liées à la méconnaissance du fonctionnement du logiciel, aussi bien au cours de la modélisation qu’au moment de l’exploitation des résultats.
Des outils existent pour accompagner cette phase de validation. On citera notamment le “Guide de validation des progiciels de calcul de structures” publié par l'AFNOR 1990 (ISBN 2-12-486611-7). Ce guide, établi initialement pour la validation des logiciels pour les développeurs, fournit une base de données de test et d’exemples simples de modélisation, accompagnés des résultats corrects.
Il est conseillé de choisir quelques tests dans cette base de données, de les distribuer comme exercice à l’équipe et de partager les résultats, bons ou mauvais, de ces tests pour que chacun comprenne bien comment le logiciel fonctionne, les options prises par défaut et les pièges à éviter.
$translationBooksE.2 Validation d’un modèle par autocontrôle
E.2 Validation d’un modèle par autocontrôle
Avant d’exploiter les résultats du modèle, il convient de procéder à plusieurs vérifications portant sur :
-
les données d'entrée ;
-
le comportement du modèle soumis à des sollicitations et à des conditions cinématiques élémentaires ;
-
les capacités du modèle et du logiciel à fournir des résultats satisfaisants et exploitables.
Si certains de ces points s’avèrent redondants pour celui qui a lui-même réalisé la modélisation (voir paragraphe précédent), ils sont essentiels dans le cas de l’exploitation d’une modélisation réalisée par une tierce personne.
Si l’objectif final de l’étude globale est d’effectuer des calculs non linéaires (non-linéarités géométriques, loi de comportement de matériaux non-linéaires … ), cette validation s’avère primordiale car elle peut éviter l’exécution inutile de longs calculs. Ceci est d'autant plus vrai que l’obtention d’une solution acceptable pour un problème complexe à résoudre est rarement immédiate.
De manière générale, la réalisation d'un petit modèle simplifié à l'aide de barres permet de valider rapidement certains ordres de grandeur de valeurs issues d'un modèle EF. Voir à cet égard l'exemple de la tour IGH (modèle brochette): Exemple A - Immeuble de Grande Hauteur (partie C).
On s'astreindra aussi à vérifier le modèle au fur et à mesure de l'avancement du modèle, en particulier sous le cas de charge poids propre. On voit trop souvent des ingénieurs se lancer dans une modélisation de plusieurs semaines puis buter sur des messages d'erreurs multiples. Il est loisible également de sauvegarder les fichiers de données intermédiaires au long de la journée, en incrémentant le nom du fichier, de manière à pouvoir revenir à une version précédente très facilement (celle qui fonctionnait avant les derniers ajouts).
Cette approche permettra aussi d'évaluer les temps nécessaires à la génération du modèle, de calcul et d'affichage des résultats.
Quelques points de contrôle importants sont présentés ci-après. Cette liste n’est ni limitative, ni exhaustive. Pour des problèmes spécifiques, d’autres points de contrôle peuvent être envisagés.
E.2.1 Premières vérifications du modèle
Avant toute exécution des calculs, il est nécessaire de procéder à des vérifications de base.
Ces contrôles peuvent paraître fastidieux mais la détection d’erreurs, souvent basiques, peut faire gagner beaucoup de temps au final.
a) Contrôle de la géométrie du modèle
De simples contrôles graphiques permettent généralement de faire apparaître des incohérences sur les caractéristiques géométriques des éléments.
Certains logiciels permettent de visualiser les éléments avec leur vraie section. Cette possibilité est particulièrement intéressante pour les éléments de type poutres car elle permet de contrôler de visu la bonne orientation des axes principaux et la position adéquate de l’axe longitudinal qui servira de référence pour la mise en place du chargement par exemple.
La liaison des éléments, la bonne connexion des coques et les conditions aux limites font partie intégrante de la vérification géométrique. Le contrôle visuel des repère locaux avant application des charges locales, également.
b) Caractéristiques des éléments
Pour des éléments de type poutres, certains logiciels peuvent proposer des profilés prédéfinis. Lors de la toute première utilisation d’un tel élément, il convient de vérifier que les caractéristiques affichées par le logiciel correspondent bien à la géométrie ; comparer ces caractéristiques avec celles fournies par les catalogues dans le cas de profilés standard ou procéder à des calculs manuels approchés des caractéristiques pour des sections non standard.
Pour une section définie par son contour, les surfaces et inerties calculées par le logiciel doivent être vérifiées.
Pour les problèmes courbes ou avec des charges excentrées, il est important de vérifier la position du centre de torsion des poutres et de vérifier si le logiciel tient compte ou non d'un décalage éventuel entre centre de gravité et centre de torsion.
c) Pour les caractéristiques des matériaux, une relecture des données est nécessaire.
Dans le cas d’un modèle mono-matériau, une erreur sur le module de Young peut affecter les résultats des déformations sans avoir d'impact sur les efforts. Alors que dans le cas d’un modèle multi-matériaux, une erreur sur l’un des modules influencera l’ensemble des résultats.
d) Comparaison par rapport aux versions antérieures
Quand on dispose d’un modèle simplifié, issu d’une phase antérieure, ou que l’on fait une modification sur un modèle, on doit systématiquement recontrôler certaines grandeurs principales pour détecter d’éventuelles erreurs.
e) Caractéristiques des charges
Pour les charges, une relecture des données s’avère également nécessaire.
Il s’agit de visualiser l’ensemble des charges appliquées au modèle et ce pour chacun des cas de charge définis.
Les valeurs de charges doivent être correctement identifiées ; valeurs caractéristiques ou valeurs pondérées. L’orientation et la direction de ces charges doivent aussi être vérifiées.
Si le modèle contient plusieurs cas de charge, il convient d’observer s’il s’agit de cas de charges indépendants ou successifs.
Pour les études dynamiques, une vérification des masses du modèle, dans toutes les directions est indispensable.
E.2.2 Vérifications de base de résultats de calcul
Cette étape se base sur des approches simplifiées statiques linéaires.
Pour chaque calcul réalisé, des vérifications de base doivent être effectuées. Ces vérifications, en plus de participer à la validation du modèle, permettront également, pour un débutant, de se familiariser avec le post-processeur du logiciel utilisé et de vérifier que les différentes options des éléments et/ou des calculs ont été activées correctement.
a) Déformée – Ordre de grandeur des résultats
L’allure générale de la déformée est très explicite puisqu’elle donne une réponse immédiate sur le comportement de la structure à une sollicitation donnée. Elle permet de valider les hypothèses sur le schéma statique mis en place (appui simple, encastrement, …) et sur la modélisation des assemblages.
Attention aux facteurs d’amplification graphique, qui peuvent induire en erreur sur des déplacements locaux (imposer un facteur de 1 pour vérifier d’éventuelles incohérences).
En élasticité linéaire, les ordres de grandeur des déplacements doivent être satisfaisants. Leur amplitude doit être faible vis-à-vis des dimensions de la structure.
b) Descente de charges
L’équilibre statique doit être vérifié. On peut calculer manuellement les résultantes des charges appliquées dans le modèle et les comparer aux composantes de la somme des réactions d’appui affichée par le logiciel.
La répartition et la direction des réactions sur les différents appuis doivent être analysées par rapport aux degrés de liberté bloqués.
La présence d’une réaction nulle pour un degré de liberté bloqué doit être analysée. Il s’agira généralement d’un effet de symétrie.
E.2.3 Tests sur les liaisons et les assemblages
a) Réactions d’appui nulles ou non-nulles
Les réactions d’appui doivent correspondre au schéma statique.
Le signe doit également être contrôlé et permet de détecter des erreurs de référentiel pour les cas de charges.
b) Modélisation d’un assemblage
Le calcul général n’affranchit pas d’une analyse locale (et manuelle) par exemple avec un chargement à proximité d’un assemblage pour vérifier que les transferts des efforts se font de la manière attendue.
E.2.4 Tests de sensibilité sur des points spécifiques de la modélisation
On doit s’interroger quand la modélisation produit un effet (global ou local) qui varie beaucoup quand les données d’entrée évoluent. On serait alors en présence d’une instabilité de modèle.
$translationBooksE.3 Traçabilité et travail à plusieurs
E.3 Traçabilité et travail à plusieurs
S’il existe des projets où un seul ingénieur assurera l’ensemble des calculs, de bout en bout et à toutes les phases, la plupart du temps, le travail est réparti entre plusieurs personnes. Ceci nécessite de mettre en place une méthodologie particulière, décrite ci-dessous. Et même quand l’ingénieur est seul, ces éléments participent à la démarche de qualité globale et permettent de garder la mémoire du travail accompli.
E.3.1 Transmission / traçabilité / archivage
Pour le bon fonctionnement d’un projet, il est indispensable que toute modélisation puisse être transmise à une autre personne ayant les compétences requises pour l’exploiter sans perdre de temps à essayer de comprendre ce qui a été réalisé.
Pour permettre la transmission du modèle EF, et sans redéfinir les notions classiques de qualité (stockage des fichiers dans un dossier bien défini, nom de fichier explicite par rapport à la version valide du modèle), il est nécessaire de tracer par ailleurs précisément ce qui a été modélisé (dans une note de modélisation si possible, mais à défaut dans un texte simplifié qu’on peut aisément retrouver), qui listera au moins les données suivantes :
-
le logiciel utilisé ;
-
le type d’éléments employés ;
-
les caractéristiques de matériaux considérés ;
-
le principe de modélisation des appuis ;
-
la représentation par croquis des grands principes de la modélisation géométrique (simplifications effectuées notamment);
-
le principe de numérotation des nœuds et des éléments ;
-
les chargements appliqués ;
-
les calculs effectués ;
-
les combinaisons réalisées.
En cas de modifications des modèles au fur et à mesure des projets, il est nécessaire de s’astreindre à noter les modifications effectuées à chaque étape pour pouvoir retrouver les effets de telle ou telle modification sur les résultats obtenus et de sauvegarder les modèles intermédiaires qui ont servi. Il faut les ranger et les identifier. On se méfiera des noms qui à l'instant t semblent vouloir dire quelque choses et qui 6 mois plus tard ne sont plus compréhensibles (“test_appui_2_z_souplesse”, par exemple).
Dans le cas de programmes fonctionnant par lignes de codes, voir le paragraphe suivant.
E.3.2 Code bien écrit et commenté
Dans le cas d’un modèle monté directement dans l’interface, l’utilisateur n’a pas accès à toute la démarche de construction du modèle.
A l’inverse, dans le cas de programmes EF fonctionnant par lignes de codes, on pourra avantageusement tirer profit des options qui tracent toute la démarche de construction du modèle. Cela permet de retrouver tout le raisonnement et de comprendre comment le logiciel a créé pas à pas les différentes parties de la structure et les chargements.
Il est nécessaire d’utiliser au maximum les options de commentaires pour expliciter chaque ligne de code ou groupe de lignes de code, pour retrouver rapidement les données spécifiques que l’on recherche dans le modèle et pour qu’une personne ne connaissant pas parfaitement le langage du logiciel puisse au moins cerner les grands principes de la modélisation.
E.3.3 Réflexion sur le BIM
Le BIM (Building Information Modeling) est actuellement une nouvelle méthode de travail s’appliquant aux différents métiers de la construction. Cette approche vise à interconnecter les différents métiers pour créer une maquette unique issus de multiples fichiers.
La connexion des modèles de calculs aux modèles géométriques commence à être développée par les éditeurs de logiciel.
Néanmoins, il convient d’être vigilant et de ne pas prendre pour argent comptant toutes les options présentées comme automatiques. En effet, la modélisation EF se fonde sur une approche d’ingénieur, pour ne modéliser que ce qui est utile et nécessaire, alors que la modélisation géométrique vise à fournir des informations complémentaires inutiles pour le dimensionnement mécanique.
Le modèle géométrique est créé pour présenter des plans et vues 3D d’une structure, ainsi que les interfaces entre la structure et les équipements, et pour détecter d’éventuels conflits en volume. Il n’est pas créé pour que les connexions des éléments soient mécaniquement correctes. Il ne distingue pas les éléments principaux structurels des éléments secondaires (non structurels) qui ne doivent pas être pris en compte. Il n’intègre aucune des simplifications décrites ci-avant et qui sont importantes pour bien appréhender le fonctionnement de la structure (par exemple le décalage de l’axe neutre d’élément successifs ou le retraitement pour obtenir les nœuds).
Ainsi l’utilisation de modèles EF issus automatiquement des modèles géométriques ne procure pas forcement un gain de temps en comparaison de la méthode classique, étant donnés la nécessité de contrôle exhaustif du modèle EF, d'une part, et le temps de reprise du modèle EF pour le rendre conforme aux objectifs voulus, d'autre part.
Ceci est vrai au moment où ces lignes sont rédigées, mais les éditeurs apportent chaque jours des améliorations à leurs produits, ce qui pourrait rendre caduque le texte précédent.
L’utilisation du BIM, dont l’objectif est de faciliter les échanges avec les autres métiers, ne doit en aucun cas faire perdre de vue que la modélisation EF est un autre métier, fondé sur la valeur ajoutée du regard de l’ingénieur.
En tout état de cause, l'usage du BIM pour obtenir un modèle compatible avec le calcul oblige à repenser la séquence traditionnelle de modélisation (ingénieur/projeteur), redéfinir les responsabilités vis-à-vis de l'information … ce qui conduit à définir des processus spécifiques pour le projet.
Exemple de structure dont le modèle de calcul est issu directement de la maquette BIM:
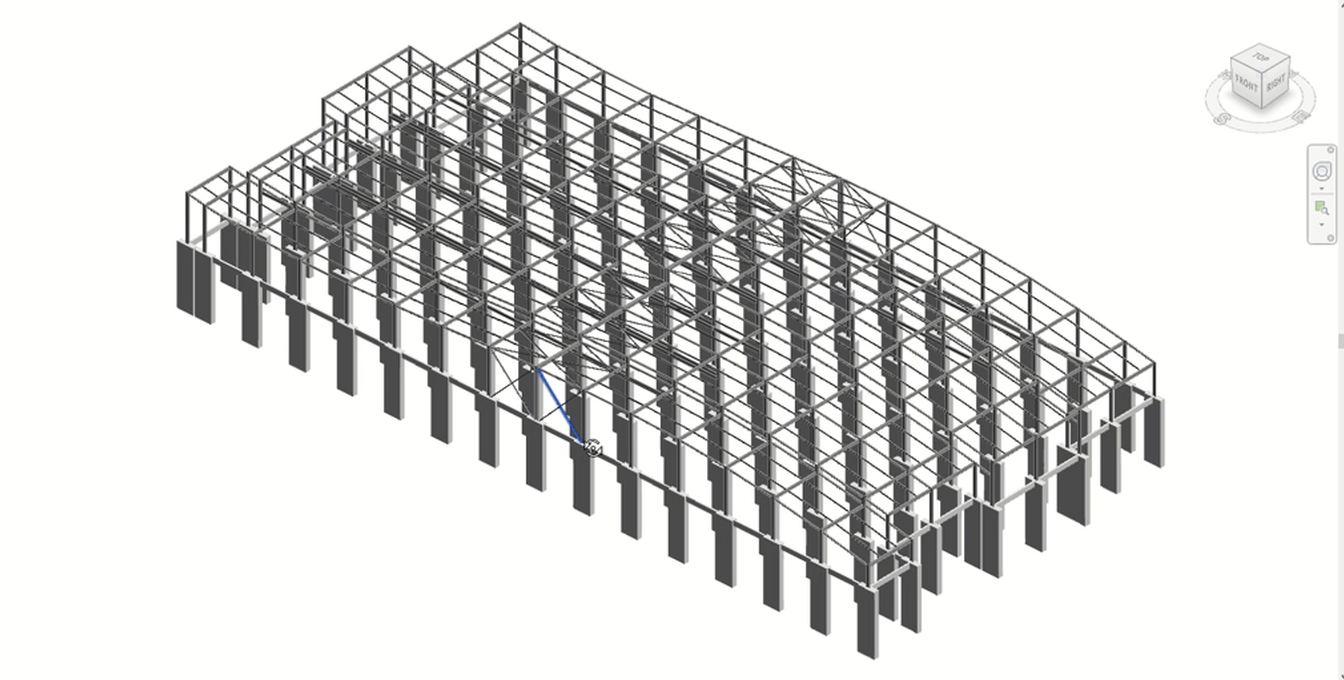
Maquette BIM
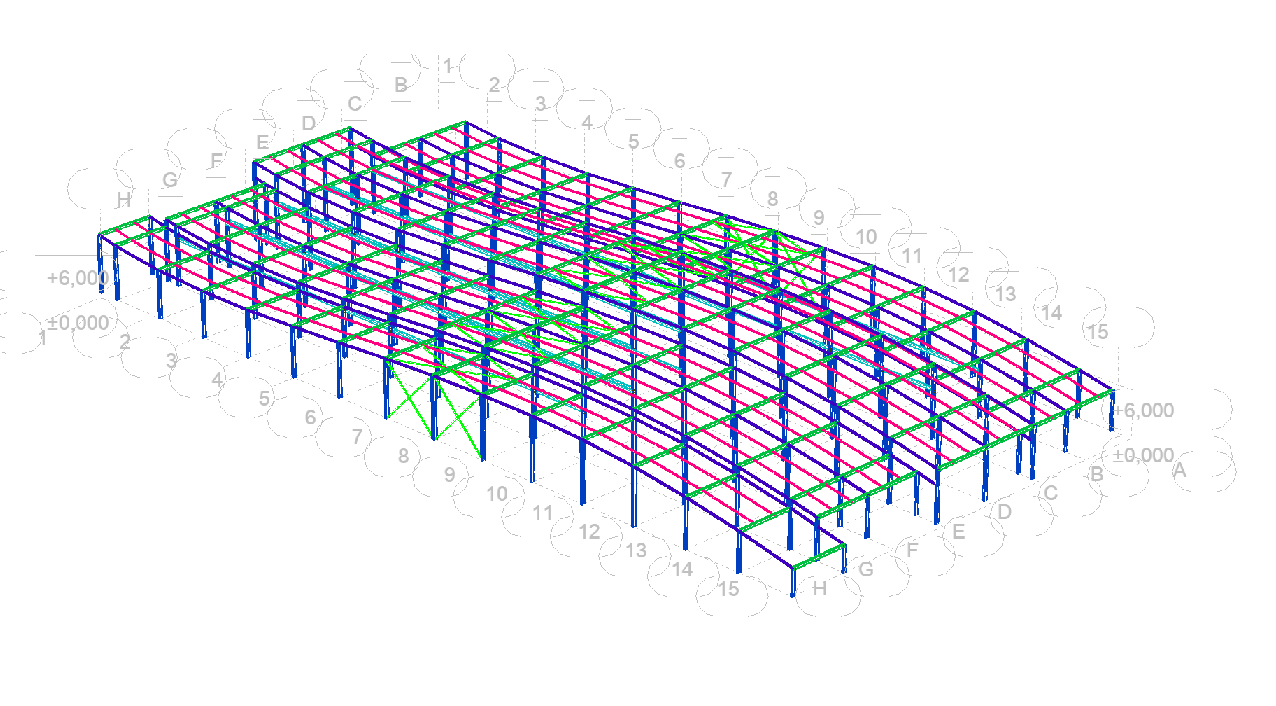
Modèle EF issu de la maquette BIM
$translationBooksChapitre F. Comment bien présenter la note de calcul aux éléments finis ?
Chapitre F. Comment bien présenter la note de calcul aux éléments finis ?
Le présent paragraphe fournit les éléments minimaux qui doivent figurer dans une note, si l’on veut fournir une description claire d’un modèle de calcul aux éléments finis.
F. Comment bien présenter la note de calcul aux éléments finis ?
$translationBooksF. Comment bien présenter la note de calcul aux éléments finis ?
F. Comment bien présenter la note de calcul aux éléments finis ?
Le présent paragraphe fournit les éléments minimaux qui doivent figurer dans une note, si l’on veut fournir une description claire d’un modèle de calcul aux éléments finis.
Avant toute chose, la note de modélisation ne peut être la première note du projet. Elle est soit précédée soit accompagnée de la note d’hypothèses générales. La note d’hypothèses générales fournit des informations indispensables sur les matériaux, sur les raideurs des fondations, sur les cas de charges et combinaisons et sur l’ensemble des justifications qu’il va falloir mener sur la structure. Idéalement, les deux notes sont rédigées en parallèle.
Trop souvent des points qui auraient toute leur place dans la note d'hypothèse ou dans la note de modélisation sont reportés à une note ultérieure. Cette façon de faire est dommageable dans la mesure où les éclaircissements arrivent ensuite avec une note “pavé” contenant les résultats et parfois même les justifications … générant des tensions avec le Maître d'Oeuvre en charge du VISA (ou le contrôleur) quand ce dernier exigera de compléter voire de refaire et surtout, des pertes de temps pour toutes les parties-prenantes.
Il est fondamental de comprendre qu'il y a un véritable effet de bras de levier en jeu et qu'il vaut mieux passer un peu de temps à détailler et fixer les éléments au départ et se les faire valider. Le déroulé de l'affaire s'en trouve grandement amélioré.
N'oublions pas que dans une mission VISA de base, la note d'hypothèses générales est la seule qui fera l'objet d'un examen approfondi par le Maître d'Oeuvre.
F.1 Introduction de la note - Description de l’objet du calcul
a) La note de calcul EF doit débuter par un bref rappel de l’objet étudié. Des extraits de plans sont toujours bienvenus.
b) Il faut également rappeler la phase d’étude. Si la phase d’étude est avancée, il est intéressant de rappeler comment le sujet a été traité aux phases précédentes. Parfois, un modèle plus simple a été développé à la phase précédente, parfois c’est un calcul à la main qui a été fait. Dans les deux cas, la note doit comparer les résultats du modèle simplifié et du modèle plus complet.
c) Il convient de préciser les objectifs du calcul, c’est-à-dire les justifications qu’on entend mener grâce à ce modèle : stabilité globale, efforts internes, déformations … Le modèle n’est pas un objectif en soi, il n’est qu’un outil pour obtenir un résultat.
d) Il n’est pas obligatoire d’utiliser un seul modèle pour toutes les justifications d’un projet. Préciser ce qui ne sera pas couvert par le modèle présent mais par un autre sous-modèle.
e) La note de modélisation doit déclarer toutes les références documentaires utilisées : les plans avec leur indice, les pièces du marché, les notes de calcul ou géotechniques.
f) En cas de mise à jour de modèle, les modifications apportées doivent être tracées de manière explicite.
g) La note doit décrire le principe d’exploitation des résultats, les sortants directs du logiciel et les éventuels post-traitements qui sont envisagés.
F.2 Description géométrique du modèle
a) Il convient de définir très clairement le périmètre physique de l’étude : les éléments qui sont modélisés et ceux qui ne le sont pas. Certaines structures secondaires n’ont souvent pas besoin d’être modélisées (escaliers ou passerelles de visite, équipements). Certaines structures principales peuvent être simplifiées comme les culées de pont ou les pieux, qui peuvent le cas échéant, être représentés par des appuis avec leur souplesse. En cas de succession d’ouvrages, les limites de modélisation doivent être décrites avec la façon de prendre en compte l’interaction avec les ouvrages adjacents non modélisés.
b) Les hypothèses de simplification de la géométrie, du choix des nœuds et des sections doivent être exposées dans le détail. La fourniture d’un listing complet du fichier de calcul ne peut pas répondre à cette demande. Il faut des schémas. Les croquis à la main, que l’ingénieur utilise quand il code, peuvent avantageusement être fournis. Ils permettent de comprendre la logique de modélisation.
c) S’il y a un échange entre le logiciel de dessin et le logiciel Eléments Finis, il est intéressant de l’indiquer.
d) Il faut expliciter toutes les unités utilisées : distances, efforts, contraintes et masses. Par défaut, on privilégiera le système S.I.
e) Il faut définir le repère global du modèle et rappeler la convention de signes des efforts pour toutes les réactions d’appui.
f) Il en va de même pour les éléments finis: il convient d'indiquer les repères locaux et les conventions de signes adoptées par le logiciel pour les efforts et contraintes. g) Les images et sorties graphiques sont intéressantes pour visualiser le modèle, mais elles doivent être annotées et accompagnées des explications correspondantes. Une note de modélisation constituée d’une série de copies d’écran n’est pas acceptable.
F.3 Description des éléments finis
a) Comme évoqué au chapitre B, le choix du logiciel dépend de nombreux critères. Il faut expliquer, même de manière succincte, pourquoi le logiciel utilisé est approprié. S’il a des limites de calcul, ne pas hésiter à l’écrire et à expliquer comment on va parer à ces limites.
b) Description des propriétés des EF : cette partie est souvent manquante dans la description, or certains logiciels ont une grande variété de types d’éléments qui n’ont pas les mêmes fonctionnalités. En particulier, pour les modélisations en plaque, les éléments prennent ou non en compte les effets membranaires, ce qui peut changer les résultats ; il en est de même en 1D pour la déformation à l’effort tranchant dans les poutres.
c) Il faut décrire le nombre de nœuds, la taille des éléments, le type de mailles. Si un test de raffinement de maillage a été mené (comme conseillé au paragraphe d), le signaler.
d) Pour un modèle à barres, il faut fournir un tableau des caractéristiques mécaniques des barres.
e) Il faut illustrer par des captures d’écran le lien entre le repère global et les repères locaux. La plupart des logiciels ont des modes d’affichage des repères assez explicites. A noter qu’il est souvent possible et utile de forcer les repères pour faciliter l’analyse des résultats.
f) Il est intéressant de donner le nombre d’éléments ainsi que le nombre de degrés de liberté du modèle.
F.4 Description mécanique du modèle
a) Les caractéristiques des matériaux doivent être exposées de manière complète : masse volumique, module de Young, coefficient de Poisson, loi de comportement statique, lois de retrait, de fluage ou de relaxation …
b) Les conditions aux limites doivent être correctement décrites. Le schéma statique doit être rappelé, avec la façon dont sont modélisés les appuis. Si une matrice de raideur est introduite, expliquer comment elle a été calibrée à partir des paramètres géotechniques.
c) En cas de présence d’appareils d’appui, préciser s’ils sont modélisés par des barres avec des caractéristiques particulières ou par des liaisons spéciales dans le modèle.
d) Il faut lister les éléments non structuraux (équipements) et préciser lesquels sont modélisés ou a contrario pris en compte comme des charges. Comme indiqué au c), ce choix dépend de la raideur et de la masse de ces éléments non structuraux.
e) Le mode d’introduction des efforts et des charges ne va pas de soi. Il faut préciser si le logiciel fait du placement automatique des charges, du positionnement incrémental des charges ou si les cas de charges sont rentrés manuellement.
f) En cas d’effort à introduire sur une coupure, il faut illustrer comment cet effort se diffuse dans le modèle (araignée reliant les bords de la coupure).
g) De manière générale, et en particulier pour les calculs sismiques ou dynamiques, il faut détailler comment sont introduites les masses dans le modèle. Si la masse des éléments est générée automatiquement par le logiciel, dans les zones d’assemblage, il y a des volumes comptés en double ; il faut donc pouvoir corriger les masses volumiques. Les éléments non structuraux modélisés par des cas de charge ne sont pas reconnus en tant que masses et doivent être ajoutés. Une vérification à la main de la masse globale du modèle est toujours utile et rassurante.
F.5 Démonstration de la démarche d’autocontrôle
L’autocontrôle est un élément fondamental de la qualité d’une modélisation.
Cette démarche d’autocontrôle doit être visible pour la personne qui va contrôler la note de calcul.
a) Les tests et éléments de vérification sur la validité du maillage doivent être mentionnés.
b) Tous les tests de validation du modèle qui ont été menés concourent à mettre en confiance le contrôleur. Il ne s’agit pas de fournir une grande quantité d’informations et de données, mais juste d’indiquer les tests qui ont été menés.
c) En revanche, les tests de vérification des descentes de charge sont absolument indispensables. Ils doivent a minima comprendre le poids propre structurel, le poids propre des équipements, une charge uniformément répartie et les cas de charges thermiques.
d) Ceci inclut également la vérification globale des masses pour les modèles dynamiques et sismiques.
F.6 Description de la récupération et du post-traitement des efforts
a) Il faut décrire sous quelle forme sont récupérés les efforts ou déplacements du modèle (listings, lecture graphique, affichage à l’écran).
b) Dans le cas où les résultats sont exprimés dans un repère local et qu’un changement de repère est nécessaire a posteriori, le risque d’erreur est fréquent. La validité du changement de base doit être démontrée.
c) De manière générale, il faut décrire le processus de post-traitement des efforts, avec les tests associés.
d) Pour les combinaisons et enveloppes, il faut dire si elles sont faites par post-traitement ou directement par le logiciel. Dans le second cas, il faut indiquer si les combinaisons sont formées à la main ou si elles sont automatiques (source d’erreur). Dans tous les cas, il faut préciser si les combinaisons et enveloppes génèrent des efforts concomitants ou non.
F.7 Présentations des résultats
Les résultats sont souvent présentés sous forme de tableaux, parfois lourds à décrypter.
a) Comme dit précédemment, le système d’unités doit être défini et il faut systématiquement indiquer les unités dans les colonnes de tableaux.
b) Il faut rappeler les descentes de charges pour les cas de charge élémentaires.
c) Il faut mettre en valeur (surligner, entourer ou mettre en gras ou en rouge) les valeurs dimensionnantes des tableaux.
d) Les listings de résultats ne doivent pas être dans le corps du texte. Ils alourdissent la compréhension du document et donnent lieu à des impressions inutiles. Ils seront placés en annexe.
F.8 Compléments spécifiques pour les éléments volumiques
a) Le choix des sections de coupe doit être cohérent avec l’exploitation attendue des résultats et doit coller aux plans critiques de l’ouvrage.
b) De la même manière que pour les éléments surfaciques, les logiciels proposent une grande variété d’éléments volumiques, avec des codes différents. Certains éléments sont très spécifiques à certains matériaux et certains types de calcul. Il faut se référer à la notice du logiciel pour choisir, sauf besoin très particulier, l’élément « le plus simple ».
c) Il convient de privilégier les résultats sous forme de cartographies, en mettant en valeur les points dimensionnants et en précisant si ce sont des valeurs lissées ou aux noeuds par exemple.
d) Dans le cas d’intégration des efforts sur une coupe, il est utile d'expliciter la méthode retenue.
F.9 Compléments spécifiques pour les calculs non-linéaires
a) Il faut fournir la loi de comportement utilisée, qui peut être différente de la loi standard du logiciel.
b) Il est intéressant de présenter, dans la note de calcul, l’évolution d'une grandeur remarquable (déplacement d'un point, effort spécifique, etc.) au cours de l'augmentation du chargement, pour visualiser une plastification.
F.10 Compléments spécifiques pour les calculs dynamiques
a) Si on utilise un spectre automatiquement fourni par le logiciel, il faut démontrer qu’on a vérifié que ce spectre est conforme à celui qu'on attend.
b) Il faut définir les amortissements retenus (qui ne sont pas les mêmes en dynamique et en sismique) et/ou les coefficients de comportement pour les calculs sismiques.
c) Il faut donner les masses participantes, les coefficients de participation des modes, mode par mode et préciser les combinaisons modales retenues ainsi que les signatures modales choisies, s’il y a lieu.
d) Il faut présenter les déformées modales pour les modes les plus représentatifs. La forme des modes est un élément important de vérification du comportement global de la structure.
e) Pour un calcul par pas de temps, comme pour le calcul non-linéaire, il est intéressant de présenter l'évolution temporelle des grandeurs représentatives (déplacements, accélérations)
PARTIE 3 - EXEMPLES DE CAS D'ÉTUDE COMPLETS
$translationBooksEXEMPLES DE CAS D'ÉTUDE COMPLETS
Cette partie contient des exemples de modélisations, pour des objets simples ou plus complexes, sous forme d'études complètes ou partielles, ou encore de comparatifs de modélisations pour une même structure.
Si vous possédez un exemple en stock que vous souhaitez partager (cela peut être une note d'un projet réel rendu anonyme), ou une complexité ou un paradoxe relevé sur un bout de modèle, proposez-nous votre contribution à l'adresse suivante: elements.finis@afgc.asso.fr.
Exemple A - Modélisation d'un immeuble complexe de grande hauteur
Exemple A - Exemple de modélisation d'un immeuble complexe de grande hauteur
Exemple B - Modélisation des ponts mixtes
Exemple B - Modélisation des ponts mixtes et métalliques
Exemple C - Modélisation de grillages de poutres
Exemple C - Modélisation de grillages de poutres
Exemple D - Exemple simple : modélisation d'une roue Br
Exemple D - Modélisation d'une roue Br
Exemple E - Flexion transversale d'un caisson en béton précontraint
Exemple E - Flexion transversale d'un caisson en béton précontraint
Exemple F - Calculs dynamiques de réservoirs
Exemple F - Calculs dynamiques de réservoirs
Exemple G - Pont à haubans
Exemple A - Immeuble de Grande Hauteur
Exemple A - Immeuble de Grande Hauteur
Exemple de modélisation d'un immeuble complexe de grande hauteur:
-
Franck DUBOIS - Structures Engineering
-
Thierry RICHARD - Structures Engineering

Partie A : Présentation de l’exemple
Objectif de l’exemple
Cet exemple concerne le calcul des efforts généraux d’un immeuble complexe de grande hauteur, au moyen d’une modélisation aux éléments finis globale.
Ce calcul intervient au démarrage des études d’exécution, son objectif concerne dans un premier temps la détermination des ferraillages des fondations (parois moulées et barrettes) du socle afin de pouvoir démarrer les forages des parois et barrettes.
Puis dans un deuxième temps, la modélisation sera utilisée pour calculer les efforts généraux dans les voiles et planchers nécessaires aux calculs des ferraillages des différents éléments (voiles, poteaux, planchers).
Cet exemple étudie en particulier les points sensibles de la modélisation de cet immeuble :
-
l’interaction sol structure ;
-
les calculs sismiques ;
-
les calculs non linéaires ;
-
ainsi que les calculs phasés.
Une attention particulière est portée sur la gestion de la modélisation, en détaillant sa préparation, son intégration dans l’étude générale, son organisation et sa validation.
Présentation du projet
Cet immeuble est situé à Monaco en site urbain majeur, au milieu de terrains à pendages importants. Il est constitué de 2 zones importantes :
-
un socle enterré dans sa zone arrière sur 13 niveaux constitué par des parkings en arrière et des logements comprenant une école sur le devant côté mer ;
-
une tour sur 25 étages reposant sur une partie du socle.
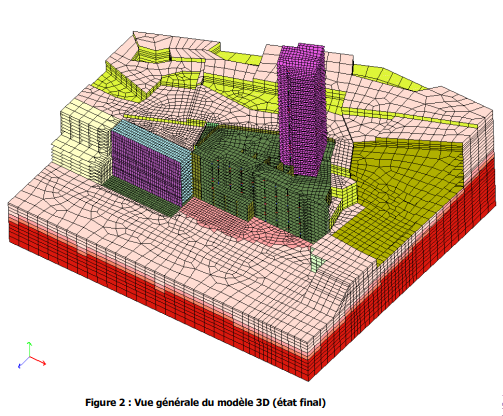
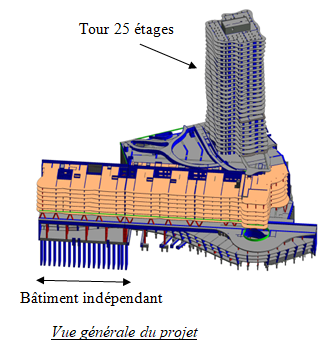
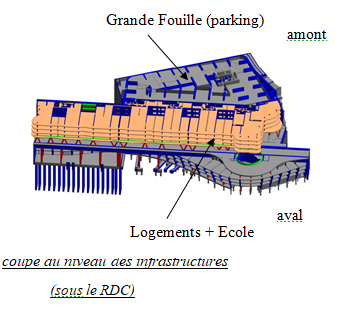
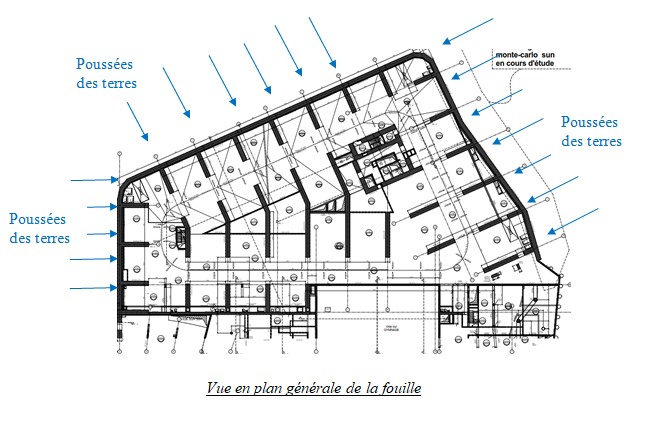
Partie B : Préparation et organisation de la modélisation
Cliquez sur le lien suivant pour accéder à la partie B: https://wiki-gtef.frama.wiki/_media/Exemple_modelisation_immeuble_grande_hauteur-partie_B.pdf
Partie C : Réalisation de la modélisation
Cliquez sur le lien suivant pour accéder à la partie C: https://wiki-gtef.frama.wiki/_media/Exemple_modelisation_immeuble_grande_hauteur-partie_C_.pdf
Partie D : Calculs de la modélisation globale
Cliquez sur le lien suivant pour accéder à la partie D: https://wiki-gtef.frama.wiki/_media/Exemple_modelisation_immeuble_grande_hauteur-partie_D.pdf
Partie E : Validation de la modélisation et calculs des ferraillages
Cliquez sur le lien suivant pour accéder à la partie E: https://wiki-gtef.frama.wiki/_media/Exemple_modelisation_immeuble_grande_hauteur-partie_eet_F.pdf
Fichier complet: https://cloud.afgc.asso.fr/s/NBwg2PiTgEgwKGf
$translationBooksExemple B. Bipoutres mixtes et métalliques
Exemple B. Bipoutres mixtes et métalliques

Le sous-groupe en charge de ces exemples travaille encore sur le sujet. Un peu de patience sera nécessaire.
-
Ouvrage mixte
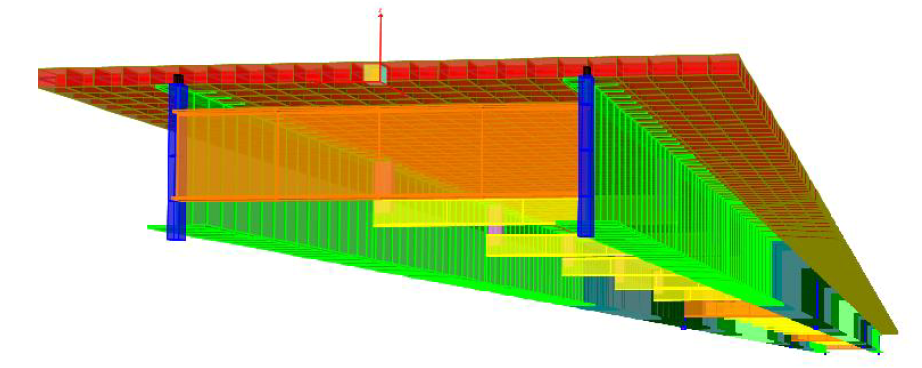
Ce sous-groupe a étudié un même ouvrage de 3 façons différentes:
-
une approche filaire 2D (lien) - Valentina Bruno (Setec tpi) ;
-
un modèle grillage de poutres 2D - Hugues Somja (INSA de Rennes) ;
-
un modèle 3D - Aymeric Perret du Cray (Setec tpi).
-
Ouvrage métallique à dalle orthotrope
-
Setec pdf : 3 modèles ;
-
Arcadis: 1 modèle.

Exemple C - Modélisation de grillages de poutres
Exemple C - Modélisation de grillages de poutres
-
Benjamin Tritschler (Arcadis) - Flexion transversale d'un pont multipoutre
Lien: https://cloud.afgc.asso.fr/s/9NK3MYEiYpGwsQ7
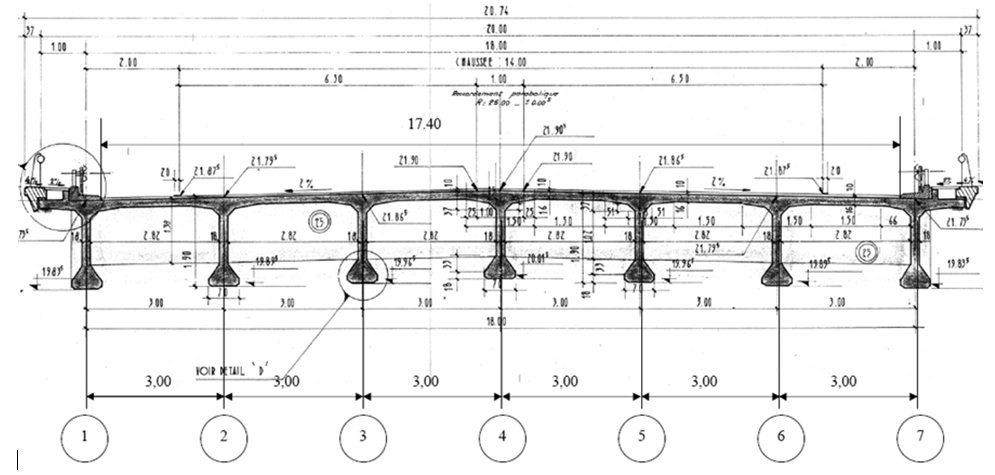
-
Jacques Combescure (Artes) - Le grillage de poutres
Lien: https://cloud.afgc.asso.fr/s/DcWCg2KWRLj2FMm
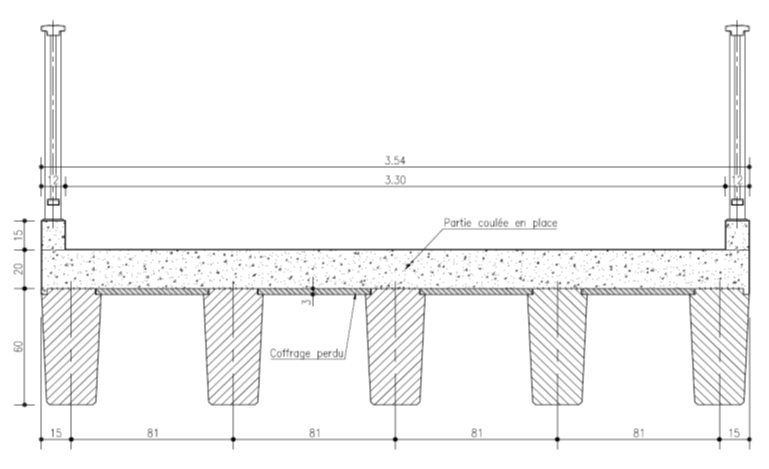
-
Pierre Perrin (Dir Est) - Contribution à l’étude des grillages de poutres
Lien: https://cloud.afgc.asso.fr/s/yP33KYxSFjJPqmW

-
Didier Guth (diadès): Modélisation d'un même ouvrage suivant différentes approches
Lien : https://cloud.afgc.asso.fr/s/KLJsLyZiC8pmmqY
Fichiers ST1 : https://wiki-gtef.frama.wiki/_media/fichiers_st1.zip
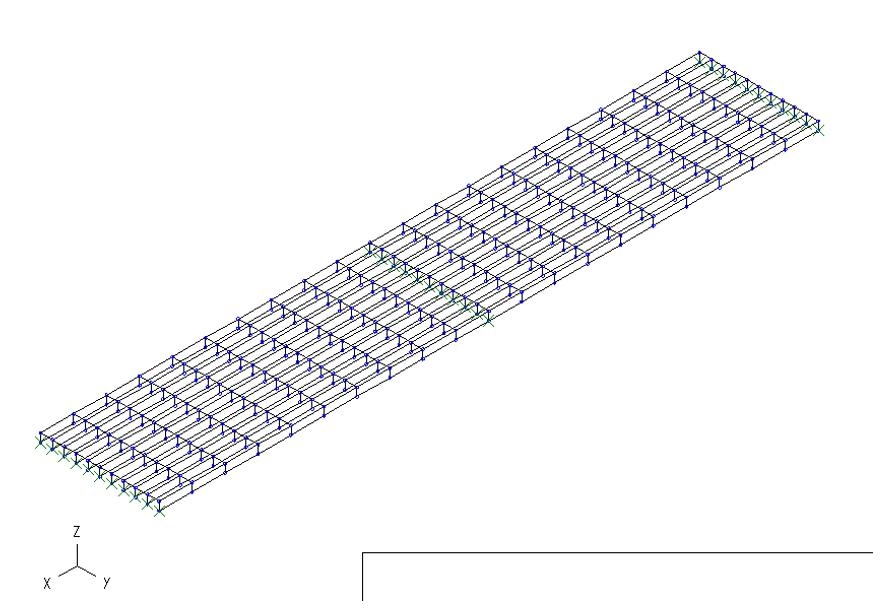
$translationBooks
Exemple D - Cas simple : modélisation d'une roue Br
Exemple D - Cas simple : modélisation d'une roue Br
L'objectif de cet exemple est de montrer les écarts que l'on peut obtenir avec plusieurs logiciels différents pour un même calcul, a priori très simple et de confirmer les propositions du chapitre D.5.2.
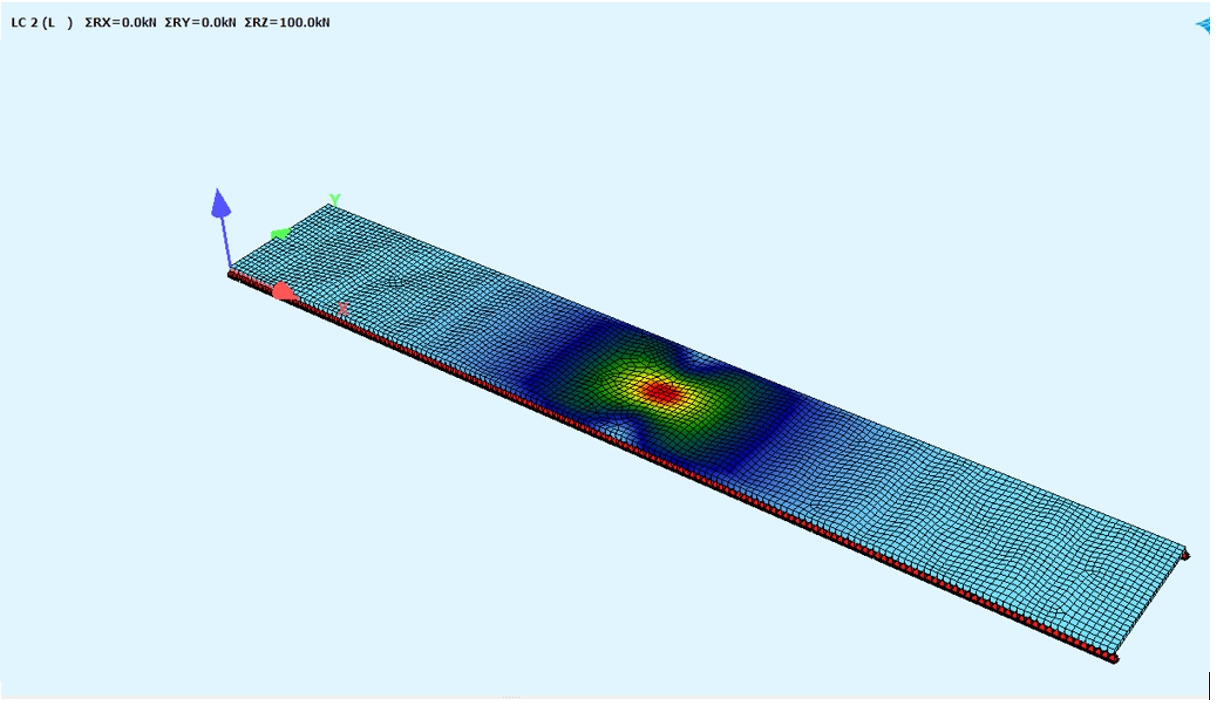
Auteurs : Franck Dubois, Valentina Bruno et Didier Guth.
Lien vers le fichier: https://cloud.afgc.asso.fr/s/58c5AX359ePN92K
$translationBooksExemple E - Flexion transversale d'un caisson en béton précontraint
Exemple E - Flexion transversale d'un caisson en béton précontraint
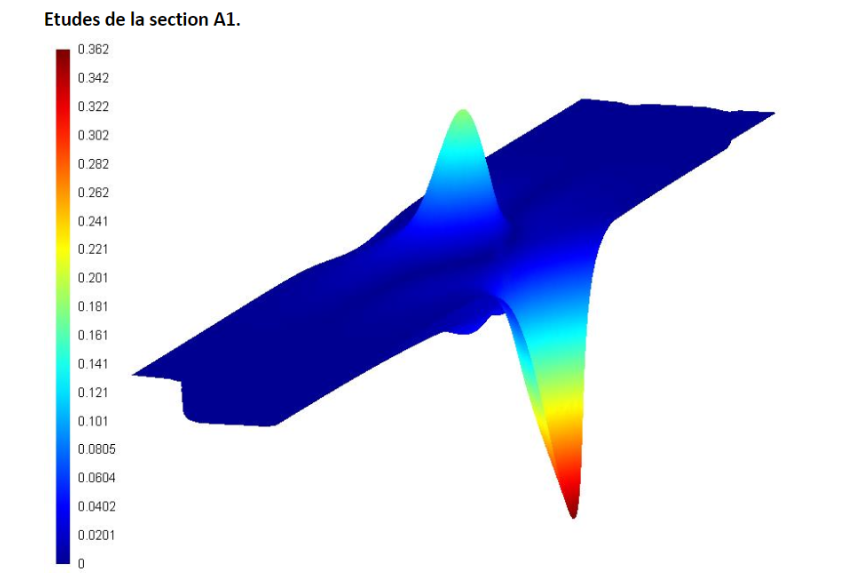
Auteur : Jean-Paul Deveaud - Cerema Centre-Est.
Lien vers le fichier: https://cloud.afgc.asso.fr/s/apaRyaTMbJpNtJg
Lien vers la coupe: https://cloud.afgc.asso.fr/s/XxmzPsxQjkpDTE7
$translationBooksExemple F - Calculs dynamiques de réservoirs
Exemple F - Calculs dynamiques de réservoirs
A venir … un peu de patience

Auteur: Gildas Potin & Al.
$translationBooksExemple G - Pont à haubans
Exemple G - Pont à haubans
A venir … un peu de patience

Auteur:
BIBLIOGRAPHIE
$translationBooksRéférences bibliographiques générales

Références bibliographiques générales
1) Ouvrages généraux
-
BATOZ, Jean-Louis DHATT, Gouri. Modélisation des structures par éléments finis (volume 1 : solides élastiques). Hermès, 1990.
-
BATOZ, Jean-Louis DHATT, Gouri. Modélisation des structures par éléments finis (volume 2 : poutres et plaques). Hermès, 1990.
-
BATOZ, Jean-Louis DHATT, Gouri. Modélisation des structures par éléments finis (volume 3 : coques). Hermès, 1990.
-
BONNET, Marc FRANGI, Attilio. Analyse des solides déformables par la méthode des éléments finis. Éditions de l'École Polytechnique, 2006, 300 p.
-
BRULE, Stéphane CUIRA, Fahd. Pratique de l'Interaction Sol Structure sous Séisme. Éditions , 2006, 300 p.
-
ZIENKEIWICZ, O. C. La méthode des éléments finis. Mc Graw Hill, Paris, 1979.
-
Collectif. Théorie de la fiabilité - Application à l’évaluation structurale des ouvrages d’art. Rapport d’études. Sétra, février 2012.
-
Collectif. NF EN 1990. Eurocode 0 - Bases de calcul des structures. Afnor, mars 2003.
2) Ouvrages pédagogiques
-
CHATEAUNEUF, Alaa. Comprendre les éléments finis. Structures : principes, formulations et exercices corrigés. Ellipses-Marketing, 2005, 272 p.
-
CRAVEUR, Jean-Charles. Modélisation par éléments finis. Dunod, 3ème édition, 2008, 328 p.
-
DEBARD, Yves. RDM 6 : mémorisation des matrices globales, méthodes de calculs. IUT du Mans. Lien vers le document.
3) Qualité de la solution EF - Estimateur d’erreur globale
-
BABUSKA, I. RHEINBOLDT, W. Error estimates for adaptative finite element computations. SIAM Journal of Numerical Analysis, 1978, 15(4):736–754.
-
ZIENKIEWICZ, O.C. ZHU, J.Z. The superconvergent patch recovery and a posteriori error estimates - Part 1 : the recovery technique. Int. Journal for Num. Met. in Eng., 1992, vol 33, 1331-1364.
-
ZIENKIEWICZ, O.C. ZHU, J.Z. The superconvergent patch recovery and a posteriori error estimates - Part 2 : error estimates and adaptivity. Int. Journal for Num. Met. in Eng., 1992, vol 33, 1365-1382.
-
DELMAS, J. Estimateur d’erreur de ZHU-ZIENKIEWICZ. [R4.10.01] Documentation CODE-ASTER, 2012.
-
DELMAS, J. Estimateur d’erreur en résidu. [R4.10.02] Documentation CODE-ASTER, 2012.
-
LADEVEZE, P. PELLE, J. La maîtrise du calcul en mécanique linéaire et non-linéaire. Lavoisier, 2001.
4) Qualité d’une quantité d’intérêt obtenue par la MEF – Estimateur d’erreur locale
-
BECKER, R. RANNACHER, R. An optimal control approach to shape a posteriori error estimation in finite element methods. Acta Numerica, 10, 2001, pp. 1-120.
-
ODEN, J. PRUDHOMME, S. Goal-oriented error estimation and adaptivity for the finite element method. Computer and Mathematics with Applications, 2001, 41:735–756.
-
DELMAS, J. Estimateurs d’erreurs en quantité d’intérêt. [R4.10.06] Documentation CODE-ASTER, 2013.
Références bibliographiques sur la dynamique
1) Ouvrages généraux
-
CLOUGH, R.W. PENZIEN, J. Dynamics of structures. Computers & Structures, 2003.
2) Ouvrages pédagogiques
-
EUVRARD, D. Résolution numérique des équations aux dérivées partielles de la physique, de la mécanique et des sciences de l'ingénieur : Différences finies, éléments finis, problèmes en domaines non bornés. Dunod, 1994.
3) Ouvrages dédiés au génie parasismique
-
BETBEDER-MATIBET, J. Génie parasismique Tome 1, 2 & 3. Hermès, 2003.
-
CHOPRA, A.K. Dynamics of structures, Theory and Applications to Earthquake Engineering. Prentice Hall, 1995.
Références bibliographiques spécifiques au génie civil
-
PRAT, M. BISCH, Ph. MESTAT, Ph. MILLARD, A. PIJAUDIER-CABOT, G. La modélisation des ouvrages. Hermès, 1995, 770 p.
-
PRAT, M. BISCH, Ph. MESTAT, Ph. MILLARD, A. PIJAUDIER-CABOT, G. Calcul des ouvrages généraux de construction. Hermès, 1995, 767 p.
-
HASHIN, Z. The elastic moduli of heterogeneous materials. 1962.
-
de LARRARD, F. Structures granulaires et formulation des bétons (2000). Etudes et Rech. Des LPC, n°OA34
-
GIMSING, N.J. Cable supported bridges (1983), Wiley & Sons
-
ACKER, P. EYMARD, R. Fluage du béton : un modèle plus performant et plus simple à introduire dans les calculs numériques. Annales de l’ITBTP, n°507, série Béton 295, 1992.
-
ARGIN, M. Stress-strain relationships for concrete and the analysis of structural concrete sections. Solid Mechanics Division, University of Waterloo, 1971.
-
GOTO, Y. Cracks formed in concrete around deformed tension bars. ACI J. Proc., n°68 (4e série), 1971, pp. 244-251.
-
BARON, J. SAUTEREY, R. Les bétons hydrauliques, Presse des Ponts et Chaussées, 2003.
-
HILL, R. Mathematical theory of Plasticity Cambridge University Press, 1970.
-
SOMJA, H. Contribution à la modélisation du comportement des ouvrages d’art lors des phases de construction avec prise en compte des non-linéarités géométriques et matérielles. Thèse de doctorat, Université de Liège, 2004.
-
GIRY, C. DUFOUR, F. MAZARS, J. Stress-based Non-local Damage Model. International Journal of Solids and Structures - INT J SOLIDS STRUCT. 48. 3431-3443. 10.1016/j.ijsolstr.2011.08.012, année 2011.
-
LORENTZ E. A nonlocal damage model for plain concrete consistent with cohesive fracture. International Journal of Fracture. 207. 10.1007/s10704-017-0225-z, année 2017.
-
PEERLINGS, R.H.J. de BORST, R. BREKELMANS, W.A.M. de VREE, J.H.P. Gradient-enhanced damage for quasi-brittle materials. Int. J. Numer. Methods Engrg, 1996, 39: 3391-3403
-
PIJAUDIER-CABOT, G BAŽANT, P.Z. Nonlocal Damage Theory. Journal of Engineering Mechanics-asce - J ENG MECH-ASCE. 113. 10.1061/(ASCE)0733-9399(1987)113:10(1512), année 1987.
-
Collectif. Practitioner's guide to finite element modelling of reinforced concrete structures. Bulletin n°45, fib, 2008.
-
VIRLOGEUX, M. Tribune libre. BOA n°14, SETRA, mars 1993.Lien vers le BOA (sujet bielles-tirants).
-
KRETZ, Th. & al. Etude des montants des cadres d'entretoisement. Bulletin des Ponts Métalliques n°18, OTUA, 1996.
Référence relative au calcul à la fatigue en métal
-
HOBBACHER, A. F. Recommendations for Fatigue Design of Welded Joints and Components. Springer - 2018.
Références bibliographiques sur les post-traitements
1) Ouvrages généraux
-
PERCHAT J. Traité de béton armé selon l’Eurocode 2. Editions Le Moniteur, 2017.
2) Référence relative au calcul des armatures de béton armé dans les plaques
-
Collectif. Algorithme de calcul des densités de ferraillage. Doc. R7.04.05, document de référence de code aster, May 4th, 2018.
3) Référence relative au calcul des armatures de béton armé par méthode bielles-tirants automatisée
-
MENDOZA-CHAVEZ G. et al.. Discrete sequential optimization for strut-and-tie design. Transactions, SMiRT-25 Charlotte, NC, USA, Division VI, August 4 -9, 2019.
Références bibliographiques spécifiques aux calculs géotechniques
-
BATHE K.J. Finite element procedures. Prentice Hall Inc, 1996, 1037 p.
-
BONNET M. Boundary Integral Equations for Solids and Fluids. Wiley and Sons, Chichester, UK, 1995.
-
CLOUGH R.W., PENZIEN J. Dynamics of structures. Mc Graw-Hill, 1993, 738 p.
-
KRAMER S.L. Geotechnical Earthquake Engineering. Prentice Hall Inc, 1996, 653 p.
-
MESTAT P., PRAT M. Ouvrages en interaction, volume 2 : la maîtrise de la modélisation des ouvrages. Hermès, 1999, 944 p.
-
LEHMANN, L. Wave propagation in infinite domains. Springer Verlag, 2007, 182 p.
-
PECKER, A. Dynamique des sols. Presses de l’Ecole Nationale des Ponts et Chaussées, 1984, 284 p.
-
POTTS D.M., ZDRAVKOVIC L. Accounting for partial material factors in numerical analysis. Géotechnique, 62, 2012, pp. 1053–1065.
-
SEMBLAT J.F., PECKER? A. Waves and Vibrations in Soils: Earthquakes, Traffic, Shocks, Construction Works IUSS Press (Instituto Universitario di Studi Superiori di Pavia), 2009, 493 p.
-
TSCHUCHNIGG F., SCHWEIGER H.F., SLOAN S.W., LYAMIN A.V., RAISSAKIS I. Comparison of finite-element limit analysis and strength reduction techniques. Géotechnique, 65, 2015, pp. 249–257.
-
WOLF, JP. Dynamic Soil-Structure Interaction. Prentice Hall Inc., 1988.
-
WOLF, JP. Soil-Structure Interaction Analysis in Time Domain. Prentice Hall Inc., 1988.
-
YOSIDA, N. Seismic ground response analysis. Springer Verlag, 2015, 370 p.
-
Collectif. Guide « Ponts courants en zone sismique ». Sétra - SNCF - 199x
-
BETBEDER-MATIBET, J. Génie parasismique – volume 3. Hermès Science Publications, 2003.
-
Collectif. Règles de construction parasismiques – Dimensionnement des ancrages en zone sismique. FD P06-029. Afnor. Décembre 2017.
Liens internet vers des documents utiles:
-
PACOSTE, C. PLOS, M. JOHANSSON, M. Recommendations for finite element analysis for the design of reinforced concrete slabs. Chambers, Stockholm, Sweden, 2012.
http://publications.lib.chalmers.se/records/fulltext/176734/local_176734.pdf
-
Site de l'ECAM: Lignes d'influences
http://clb.perso.univ-pau.fr/rdm/isa2/Codes/HTML/ligne_influence/ligne_influence.html
-
Site métalétech du CTICM: Lien: https://metaletech.com/
SUIVI DES AJOUTS ET MODIFICATIONS
$translationBooksSuivi des ajouts et modifications
Suivi des ajouts et modifications
2020/07/12: Exemple E - Calcul de flexion transversale d'un caisson BP - JP Deveaud
2020/07/27: Exemple E, ajout de la coupe cotée.
$translationBooksA3. Choix des éléments finis
A3. Choix des éléments finis
Le choix de l’élément est une étape importante. L’objectif est de sélectionner le type d’élément (à savoir sa forme et l’ordre des fonctions de forme associées) et la taille de l’élément. Le type et la taille des éléments définissent l’allure et la précision des champs de déplacement, donc, de déformation et de contraintes.
En plus, de la forme de l’élément, vient s’ajouter son aspect. Il faut éviter de produire des éléments dégénérés ou trop dénaturés (aplatis ou allongés) car cela dégrade la précision de la résolution du problème.
De manière plus globale, le maillage généré peut être structuré (répartition régulière des éléments) ou non structuré. Il est possible de combiner sur un même domaine des parties structurées et non structurées suivant la complexité géométrique.
Dans le même esprit, la taille de l’élément choisi est dépendante de la géométrie de la structure à mailler et des chargements qui lui sont appliqués. Les zones à fortes variations (gradients) de contrainte ou à contraintes élevées (contact-frottant ou fissuration par exemple) déterminent les parties nécessitant une finesse de maillage supérieure aux autres parties pour bien percevoir les contraintes ainsi que les déformations.
Une des premières règles à respecter est de lancer une première simulation avec un premier maillage afin de déterminer les zones sensibles énumérées précédemment et ensuite raffiner le maillage où cela s’avère nécessaire.
Le modélisateur doit avoir un regard critique sur son maillage vis-à-vis de la géométrie de la structure et des zones importantes à observer.
Pour bien choisir les éléments finis à utiliser lors du maillage, il est nécessaire de réfléchir au type de calcul souhaité :
-
l'ensemble de la géométrie va-t-elle être représentée, auquel cas le problème relève de la MMC et les éléments sont donc de type « massif » ; dans ce cas, il faut savoir si le problème est tridimensionnel ou bidimensionnel (contraintes planes, déformations planes, axisymétrie… cf. 3.) et si on souhaite utiliser des éléments finis à fonctions de forme linéaires ou quadratiques : la précision des calculs est meilleure avec un maillage d'éléments quadratiques mais a un coût de calcul plus important : il faut donc faire un compromis ; dans tous les cas, les degrés de liberté sont les composantes du déplacement (u, v en 2D, u, v, w en 3D) ; les principaux éléments sont listés dans le tableau ci-dessous ;

-
ou la géométrie est simplifiée, cas de la RdM (ou calcul des structures cf. 2.) : dans ce dernier cas, les éléments finis sont donc
-
des éléments de barre/poutre (une barre ne reprend que de la traction ou de la compression à la différence d'une poutre qui reprend en plus de la flexion ; attention, certains logiciels ne différencient pas les deux et parlent d'éléments de barre pour désigner également des éléments de poutre)
-
des éléments de plaque/coque (la différence entre plaque et coque est liée à la courbure du feuillet moyen et la plupart des logiciels ne font pas la distinction).
-
Pour ces éléments, en plus des degrés de liberté de déplacement, les éléments de RdM comportent des degrés de liberté de rotation (θx, θy, θz), permettant de prendre en compte la géométrie non maillée (section pour les poutres, épaisseur pour les plaques et coques). De plus, se pose la question de savoir si l'énergie de cisaillement doit être prise en compte ou pas (éléments de poutre de Navier-Bernoulli ou de Timoshenko, éléments de coque de Love-Kirchhoff ou de Mindlin-Reissner). Dans le cas des éléments de coque, comme mentionné auparavant, se pose enfin la question de la qualité des éléments (éléments conformes ou pas). Il est donc particulièrement difficile de faire le choix d'un élément fini de plaque/coque, en particulier lorsque la documentation est succincte ; il peut être judicieux dans ce cas, de réaliser un calcul sur un cas dont la solution est connue afin de tester la qualité des éléments disponibles.
En RdM, les différents éléments généralement rencontrés sont décrits dans le tableau II ci-dessous.
